生成AI的两大范式：扩散模型与Flow Matching的理论基础与技术比较

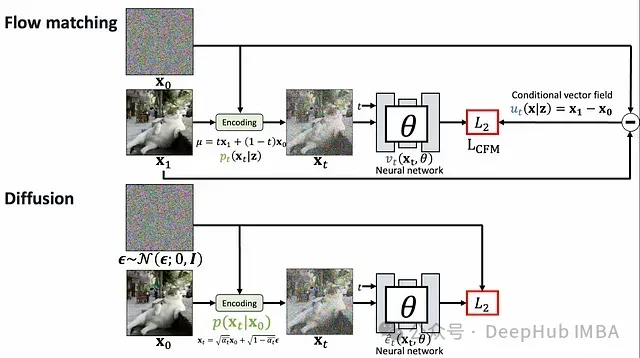
生成模型已成为人工智能领域的关键突破，赋予机器创建高度逼真的图像、音频和文本的能力。在众多生成技术中，扩散模型和Flow Matching尤为引人注目。这两种方法虽然都致力于在噪声与结构化数据之间建立转换，但其基础原理存在本质区别。本文将系统地比较这两种先进技术，深入探讨其数学原理、实际应用及理论解释。

基本原理

在深入数学分析前，有必要从直观层面理解这两种方法的核心概念：

扩散模型系统性地向数据添加噪声，直至将其转化为纯粹的随机噪声，然后学习此过程的逆向转换。这一过程可类比为将照片逐步溶解至完全模糊状态，随后从模糊中重建原始影像的过程。

Flow Matching则构建噪声分布与数据分布间的连续路径（流）。这一过程可类比为定义一种平滑的转换计划，使随机噪声逐渐形成有结构的数据，如同观察一块黏土从无序状态被塑造成精细雕像的过程。

扩散模型的数学基础

前向过程

扩散模型定义了一个前向过程，该过程在 T 个时间步长内有序地向数据 x_0 添加高斯噪声：

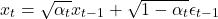
其中

且 \alpha_t \in (0, 1) 表示噪声调度参数。

此过程可通过随机微分方程(SDE)表示：

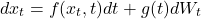
其中 W_t 代表标准维纳过程（布朗运动），f(x_t, t) 为漂移系数，g(t) 为扩散系数。

经过充分的扩散步骤，x_T 将近似标准正态分布 \mathcal{N}(0, I)，原始数据的结构信息基本完全消散。

反向过程

扩散模型的核心在于学习逆转噪声添加过程，通过从随机噪声开始并迭代去噪来生成新数据。

反向过程定义为：

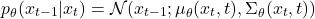
在实际应用中，诸如DDPM（去噪扩散概率模型）等模型针对每一时间步预测噪声分量 \epsilon_\theta(x_t, t)，进而推导出 \mu_\theta(x_t, t)。

训练目标

扩散模型的训练目标通常基于负对数似然的变分上界：

实践中，这一目标函数常简化为经重新加权的均方误差：

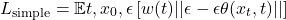
Flow Matching 的数学基础

连续归一化流与速度场

Flow Matching建立在连续归一化流(CNF)的理论之上，CNF通过微分方程将一个概率分布转换为另一个：

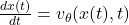
其中 v_\theta 表示可学习的速度场。

速度场的理解

速度场是一个为时空中每个点分配速度向量的函数，可类比为风向图，指示了粒子在任一位置应移动的方向与速度。在生成模型语境下：

数学定义：速度场

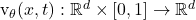
为时间 t 的每个点 x 分配一个向量 v。

物理理解：可想象为河流中任一点的水流方向与强度，决定了漂浮物体的运动轨迹。

变换特性：通过从 t=0 到 t=1 追踪速度场，可以得到样本从源分布（通常为噪声）到目标数据分布的转换路径。

速度场具有以下关键特性，使其成为生成建模的有力工具：

• 确定性路径：从给定起点追踪速度场会产生确定性轨迹
• 可逆性：通过反转速度向量可实现过程的逆向运行
• 概率质量守恒：连续性方程确保转换过程中概率质量既不创生也不消失

速度场可视化可理解为网格上每点的方向矢量：

↑ ↗ → ↗ ↑
 ↖ ↑ ↑ → ↗
 ← ↙ ↑ ↑ →
 ↙ ↓ ↓ ↗ ↑
 ↓ ↙ ← ← ↑
1.
2.
3.
4.
5.

在Flow Matching中，通过神经网络学习预测给定位置和时间的速度向量，该网络经训练以匹配定义分布间所需流的参考向量场。

概率流ODE

概率密度在流下的演化遵循连续性方程：

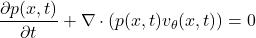
这一方程确保了变换过程中的质量守恒。

Flow Matching原理

Flow Matching的关键创新在于直接监督速度场 v_\theta，利用预定义的分布间路径。此方法避开了从复杂的概率流方程推导速度场，而是直接约束速度场匹配参考向量场 u(x,t)，后者定义了样本的移动方式：

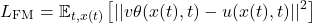
其中 x(t) 从路径分布 p_t(x) 采样，该分布在噪声分布 p_0(x) 与数据分布 p_1(x) 间插值。

条件Flow Matching

条件Flow Matching (CFM)作为重要扩展，构建了各数据点与噪声样本间的路径：

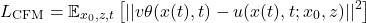
其中

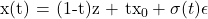
定义了噪声 z 和数据 x_0 之间的路径，

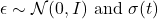
控制路径噪声水平。

主要差异分析

路径定义

扩散模型通过添加高斯噪声定义固定的随机路径。前向过程由预设的噪声调度确定，模型学习逆转这一特定过程。

Flow Matching则允许在分布间设计灵活路径。这些路径可为直线、曲线轨迹，甚至可动态学习，提供更大的设计自由度。

训练动态

扩散模型通常需要估计复杂的概率密度或其替代量，导致训练过程更具挑战性，且对噪声调度的精确设计有较高依赖。

Flow Matching直接监督速度场，形成更简洁的均方误差目标，训练过程通常更为稳定。

采样效率

扩散模型传统上需要较多采样步骤（通常1000步以上），尽管DDIM等技术已有所改进。

Flow Matching通常可利用高阶ODE求解器，以较少步骤(10-100步)实现高质量采样。

理论保证

扩散模型与基于分数的生成模型有深厚联系，并提供明确的似然界限。

Flow Matching在特定条件下对精确密度匹配提供保证，为优化概率流ODE提供更直接路径。

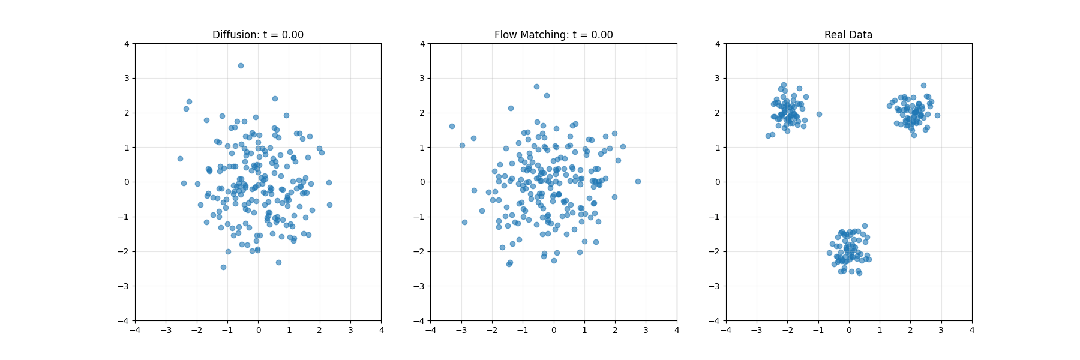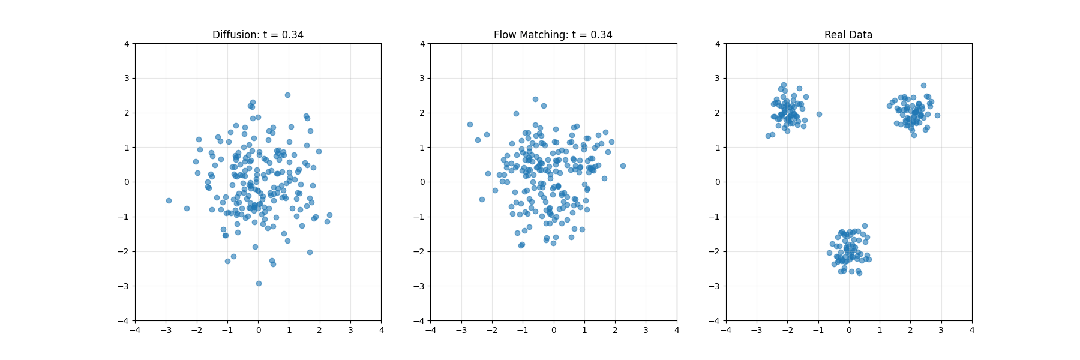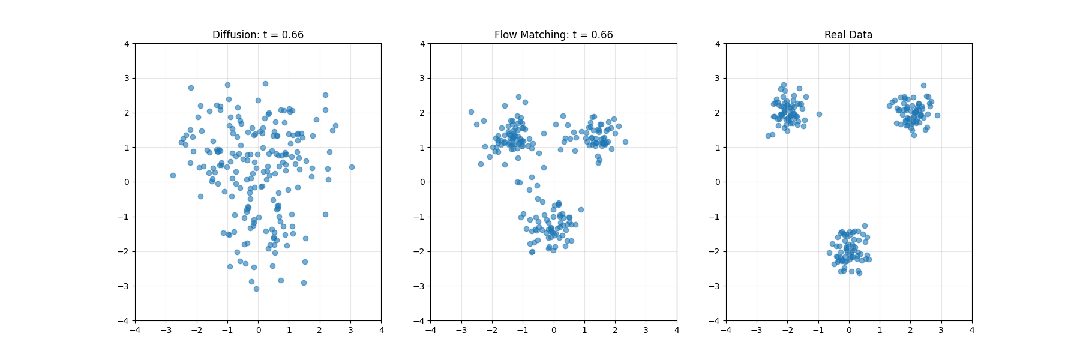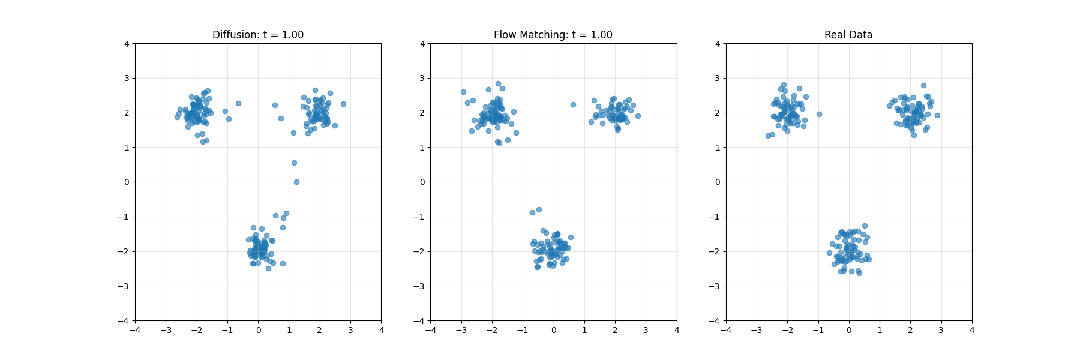
数值示例：转换简单分布

考虑将标准正态分布转换为双峰高斯混合分布的具体案例。

扩散方法

在扩散方法中，流程如下：

1. 从目标分布（高斯混合）出发
2. 按照调度 \beta_t 逐步添加噪声
3. 训练模型预测每步噪声
4. 通过从纯噪声开始并迭代去噪进行采样

对于一维示例，设定 T=10 步和线性噪声调度 \beta_t = 0.1，前向过程为：

反向过程估计：

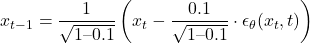
Flow Matching方法

Flow Matching方法流程为：

• 定义分布间路径，例如线性插值：

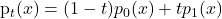
• 推导或定义诱导该路径的速度场 u(x, t)
• 训练模型预测此速度场
• 通过求解ODE：dx/dt = v_\theta(x, t) 从噪声采样到数据

对于简单示例，假设直线路径，速度场可表示为：

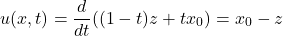
其中 z 为噪声样本，x_0 为数据样本。

实践实现与应用

扩散模型的实践

具有代表性的扩散模型实现包括：

• DDPM (去噪扩散概率模型)：奠定基础的先驱模型
• DDIM (去噪扩散隐式模型)：通过确定性过程加速采样
• Stable Diffusion：应用于潜在空间提升图像生成效率
• Imagen与DALL-E 2：基于扩散原理的文本到图像生成系统

实现关键代码示例：

# filepath: example.py
# Simplified DDPM training loop
def train_step(self, x_0, optimizer):
    """Single training step for diffusion model"""
    batch_size = x_0.shape[0]

    # Sample random timesteps
    t = torch.randint(0, self.n_timesteps, (batch_size,), device=self.device, dtype=torch.long)

    # Add noise to data
    x_t, noise = self.q_sample(x_0, t)

    # Predict noise
    predicted_noise = self.model(x_t, t / self.n_timesteps)

    # Compute loss
    loss = F.mse_loss(noise, predicted_noise)

    # Update parameters
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

     return loss.item()
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.

Flow Matching的实践

代表性Flow Matching实现包括：

• 条件Flow Matching (CFM)：高效训练生成建模的神经ODE
• 一致性模型(Consistency Models)：融合Flow Matching与扩散原理
• SiT (Score in Time)：将扩散模型重构为插值匹配框架

实现关键代码示例：

# filepath: example.py
# Simplified Flow Matching training loop
def train_step(self, x_0, optimizer):
    """Single training step for flow matching"""
    batch_size = x_0.shape[0]

    # Sample random timesteps
    t = torch.rand(batch_size, device=self.device)

    # Sample noise points
    z = torch.randn_like(x_0)

    # Get path points and target velocities
    x_t, target_v = self.sample_path_point(x_0, z, t.unsqueeze(-1))

    # Predict velocity vectors
    predicted_v = self.model(x_t, t)

    # Compute loss
    loss = F.mse_loss(predicted_v, target_v)

    # Update parameters
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

     return loss.item()
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.

概念类比

扩散模型：侵蚀与重建过程

扩散模型可类比为海滩上沙堡的侵蚀与重建。前向过程如同潮水逐渐冲刷沙堡，直至形成平坦沙面；反向过程则是学习如何通过理解沙粒运动规律，从平坦沙面重建精细结构。

Flow Matching：矢量场导航

Flow Matching类似于空间导航系统，在任一位置提供指向目标的方向矢量。无需遵循预设路线，学习的矢量场能从任意起点引导系统抵达目标分布。

方法融合与发展

近期研究显示扩散模型与Flow Matching存在深层联系：

• 概率流ODE：扩散过程可转换为类似Flow Matching的确定性ODE
• 基于分数的方法：两种方法可视为对数密度梯度（分数函数）的不同参数化
• 插值匹配：统一框架下整合多种生成方法

计算效率比较

扩散模型在采样过程中通常需要更多的函数评估，导致计算成本相对较高。然而，这类模型可以使用相对简化的架构和损失函数进行训练，在实现复杂度方面具有一定优势。

Flow Matching则通过采用复杂的ODE求解器实现更高的采样效率，但精确建模速度场可能需要更为复杂的网络架构设计。两种方法的计算效率取舍主要体现在采样速度与模型复杂度之间的平衡。

样本质量分析

两种方法均能达到先进的样本生成质量，选择应基于具体应用需求进行评估。扩散模型在处理高度结构化数据（如高分辨率图像和复杂音频）方面表现出色；而Flow Matching则在处理相对简单的分布或对采样速度有严格要求的场景中展现出明显优势。实际应用中，需权衡模型复杂度、训练稳定性、采样效率及质量要求等多方面因素。

总结

扩散模型与Flow Matching代表了生成建模领域的两类重要技术范式，各自基于独特的数学原理与实现策略。扩散模型通过定义固定的随机过程并学习其逆转，而Flow Matching则直接学习能够沿灵活路径转换分布的速度场。从某种意义上说，Flow Matching保留了扩散模型的核心优势，同时通过消除前向噪声过程的限制实现了技术简化。

深入理解这两种方法间的差异与联系，不仅有助于更全面把握生成建模的技术全貌，也为这一快速演进领域的发展提供了理论基础和研究方向。