ICLR 2025 | 西湖大学提出闭环扩散控制策略，高效与闭环兼得

本文来自西湖大学人工智能系的吴泰霖团队。本文有两位共同第一作者：魏龙是西湖大学人工智能系博士后，冯浩东是西湖大学博士生。通讯作者吴泰霖是西湖大学人工智能系特聘研究员，其领导的人工智能与科学仿真发现实验室主要研究方向为开发生成模型方法并用于科学和工程领域的仿真、设计和控制。

高效闭环控制是复杂系统控制的核心要求。传统控制方法受限于效率与适用性挑战；而新兴的扩散模型虽然表现出色，却难以满足高效闭环控制的要求。西湖大学研究团队最新提出的 CL-DiffPhyCon 框架，通过异步并行去噪技术，在闭环控制要求下，显著提升了控制效率和效果。论文最近被人工智能领域顶级会议 ICLR 2025 接收。

• 论文标题：CL-DiffPhyCon: Closed-loop Diffusion Control of Complex Physical Systems
• 论文链接：https://openreview.net/pdf?id=PiHGrTTnvb
• 代码地址：https://github.com/AI4Science-WestlakeU/CL_DiffPhyCon

一、研究背景

在科学研究、工程实践以及具身智能等诸多领域，系统控制问题都有着广泛的应用。在这些场景中，高效闭环控制是核心性能要求。例如，当机器人在复杂环境中执行任务，必须对周围环境变化做出即时反应。这就需要控制系统能够根据环境实时反馈，迅速调整控制信号，保证每一个动作指令都基于最新的环境状态生成。另外，工业制造、航空航天、能源生产等科学和工程领域的系统控制任务，同样面临着如何实现高效闭环控制的难题。

在过往的研究当中，涌现出了传统控制方法，以及近年来的深度学习、强化学习、模仿学习等众多控制方法。近期的 DiffPhyCon [1] 等研究表明，基于扩散模型 [2] 的方法在复杂物理系统控制中表现出色，尤其是对高维、长时间跨度的控制问题具有显著的优势，这主要源自于扩散模型擅长学习高维分布的特性。这类方法从离线收集的轨迹数据中学习一个去噪模型，从噪声开始，利用去噪模型逐步去噪，产生控制信号。此外，基于扩散模型的策略在机器人操作任务中也具有优异的表现 [3]。

然而，现有的扩散控制方法在应用到闭环控制时，会遇到控制效果和效率难以平衡的缺陷。它们的模型窗口内所有物理时间步，都要经历从纯噪声开始的完整去噪采样过程。若每个物理时间窗口都照此采样并将其中的最早控制信号用于控制，虽然能实现闭环控制，却会带来非常高昂的采样成本。而且，这种方式还可能会破坏控制信号的时序一致性，影响整体控制性能。反之，如果为了提高采样效率，每隔若干个物理时间步才进行一次完整采样，又脱离了闭环控制的要求。

虽然近期有研究工作提出在线重新规划策略（RDM）[4]，自适应地确定何时重新规划控制序列，但这种策略也不是真正意义上的闭环框架。它们往往需要额外的似然估计计算开销，还依赖额外的超参数。面对不同任务场景，需要多次实验来调试这些超参数，增加了应用难度和不确定性。

二、本文主要贡献

针对现有扩散控制方法在闭环控制中遇到的上述问题，本论文提出了一种基于扩散模型的闭环控制方法 CL-DiffPhyCon，它能够根据环境的实时反馈生成控制信号，实现了高效的闭环控制。该方法的核心思想是将扩散模型中的物理时间步和去噪过程解耦，允许不同的物理时间步呈现不同的噪声水平，从而实现了控制序列的高效闭环生成。论文在 1D Burgers’方程控制和 2D 不可压缩流体控制两个任务上，验证了 CL-DiffPhyCon 的显著结果。

如下图 1 中所示，该方法具有如下优势：

1. 高效采样：CL-DiffPhyCon 通过异步去噪框架，能够显著减少采样过程中的计算成本，提高采样效率。与已有的扩散控制方法相比，CL-DiffPhyCon 能够在更短的时间内生成高质量的控制信号。
2. 闭环控制：CL-DiffPhyCon 实现了闭环控制，能够根据环境的实时反馈不断调整控制策略。相比已有的开环扩散控制方法，提高了控制效果。
3. 加速采样：此外，CL-DiffPhyCon 还能与 DDIM [5] 等扩散模型的加速采样技术结合，在维持控制效果基本不变的前提下，进一步提升控制效率。

图 1：本文的 CL-DiffPhyCon（右图）相较于以往扩散控制方法（左图和中图）的优势。通过采用异步去噪框架，该方法能够实现闭环控制，并显著加快采样过程。其中，H表示扩散模型包含的物理时间窗口长度，DiffPhyCon - h表示每隔h个物理时间步进行一次包含T个去噪步骤的完整采样过程，然后将采样的控制信号序列中的前h个依次用于开环控制。这里没有展示与 DDIM [5] 的结合。

三、问题设置和预备知识

1. 问题设置：

给定初始状态、系统动力学G以及特定的控制目标，本文考虑如下复杂系统的控制问题：

这里，和分别是物理时间步时的系统状态和外部控制信号，轨迹的长度为N。系统动力学G代表系统在外部控制信号下随时间的状态转移规则。G可以是随机性的，存在非零随机噪声；也可以是确定性的，即。为了让问题设置更具一般性，状态的演变只能通过实际测量来观测，即假设G的表达形式不一定可以获得。本文中关注闭环控制，意味着每个时间步的控制信号是从以当前状态为条件的一个概率分布中采样得到的。这区别于开环控制或者规划（planning）方法，即每次规划未来多个时间步的控制信号后，将其依次应用到环境中，并且在此期间不利用环境反馈进行重新规划。

2. 预备知识：DiffPhyCon 简介

DiffPhyCon [1] 是近期发表的一种基于扩散模型的规划（planning）方法。它提前规划一个物理时间窗口（horizon）内所有的控制信号，并依次将其用于系统的控制过程。为了记号方便，引入变量表示第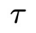物理时间步系统状态和控制信号的拼接。该方法包含以下过程：

1. 首先离线收集大量的轨迹数据，每条轨迹包括初始状态、控制序列和相应的状态序列。
2. 然后，用这些离线轨迹训练一个去噪步数为T，物理时间窗口为N的扩散模型，并将所有物理时刻的系统状态和控制信号的联合隐变量作为扩散变量。这里在记号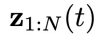中，用下角标表示物理时间或其所处的区间，用括号里的t表示扩散步骤。在扩散过程中，随着t增大，中的噪声程度逐渐增加：不含噪声，为高斯噪声。
3. 在去噪过程（实际控制过程）中，以系统的初始状态为条件，利用训练的扩散模型，在控制目标的梯度引导下，让t从T 降到 0，将高斯噪声逐步去噪为不含噪声的，其中包含控制序列和对应产生的状态序列。
4. 最后，将控制序列逐步输入到环境中，实现对系统的控制。

上述过程中隐藏了一个假设：轨迹长度N 较小，这时H 取值为N。而实际问题中更为常见的情形是N 很大，这导致物理时间窗口为N的扩散模型难以在 GPU 中运行或者物理时间跨度太大导致偏离闭环要求过远。这就需要训练一个时间窗口相对较小（H<N）的扩散模型，然后每隔h个物理时间步进行一次完全的去噪过程，或者以自适应的方式确定何时重新规划控制序列 [4]，如图 1 左边和中间子图所示。

四、CL-DiffPhyCon 方法介绍

该方法考虑的也是H<N的情形。关键想法是：将扩散模型的模型时间窗口内的物理时间和扩散（去噪）过程解耦，越早的物理时间赋予越快的去噪进度，也就是越低的噪声程度。如此一来，既实现了不同物理时间步的并行采样，提高了采样效率；又能让更早采样到的控制信号所产生的环境反馈用于后续物理时间的控制信号采样，实现了闭环控制。

为了方便，本文首先引入了如下两个记号：

• 同步联合隐变量：表示在物理时间区间内，对每个分量加入相同程度噪声。这里t的取值范围是 0 到T。
• 异步联合隐变量：表示在物理时间区间内，为越晚的物理时间赋予越高的噪声程度，即实现了物理时间和去噪进度的解耦。这里t的取值范围是 0 到。

针对这两种变量，本文训练了两个扩散模型：同步扩散模型和异步扩散模型。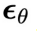

1. 同步扩散模型：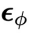

这个模型预测同步联合隐变量当中每个分量包含的噪声。它只用于的物理时刻。训练损失如下：

训练这个模型的目的，是为了采样异步联合隐变量，这是物理时间上最早的异步联合隐变量。采样方法如下：对于给定的初始条件，类似于 DiffPhyCon 的去噪过程，从高斯噪声开始，让t从T逐步减少到，在每步迭代中，从当中减去预测的噪声，同时减去控制目标的梯度。这样就采样得到了一系列同步联合隐变量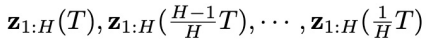。再从其中取 “对角线”，就能得到初始的异步联合隐变量（图 2 的 (2) 子图中的虚线红框）。

2. 异步扩散模型：

这个模型预测隐变量中每个分量包含的噪声。它用于的所有物理时刻。它的训练损失如下：

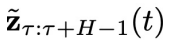训练这个模型的目的，是为了在给定第个物理时刻的系统状态和异步联合隐变量的条件下，采样，即实现解耦的异步去噪。采样方法如下：从开始，让t从逐步减少到 0，在每一步中，从当中逐分量减去预测的噪声，同时减去控制目标的梯度，最终得到。

3. 闭环控制过程

基于以上两个训练好的扩散模型，闭环控制的循环过程如下（分别对应图 2 中从左向右 4 个子图）：

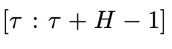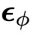• 第（1）步：在第个物理时间步，获得物理时间窗口内的初始状态和系统状态。特别地，当时，通过上文的同步扩散模型采样得到。
• 第（2）步：以为采样条件，利用异步扩散模型，从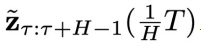开始连续采样步，得到。
• 第（3）步：将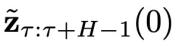的第 1 个分量中包含的控制信号输入到环境中，得到下一个状态。
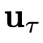• 第（4）步：采样一个高斯噪声，拼接到第（2）步采样得到的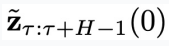的最后个分量的结尾，得到物理时间窗口内的初始状态，同时将作为条件，进入下一个物理时间步。

图 2：CL-DiffPhyCon 用于闭环控制的流程：(1) 获取当前物理时刻系统状态和 “对角线形” 异步联合隐变量；(2) 利用异步扩散模型去噪；(3) 将采样到的控制信号应用到系统；(4) 获取系统反馈的最新状态和更新后的 “对角线形” 异步联合隐变量，进入到下一个物理时刻。

4. 与扩散模型加速采样技术的结合

值得一提的是，CL-DiffPhyCon 还可与扩散模型领域的快速采样技术相结合，进一步提升采样效率。例如，DDIM [5] 通过特定的采样策略减少了采样步数，在不损失太多采样质量的前提下加快了采样速度。在 CL-DiffPhyCon 的同步和异步模型的采样过程中引入 DDIM，能够使得 CL-DiffPhyCon 在保持控制性能基本不变的前提下，以更快的速度完成采样和控制信号生成，从而在实际应用中更具优势。论文通过实验结果验证了这一点，这说明 CL–DiffPhyCon 具有和已有的扩散模型领域加速采样方法相独立的加速效果。

四、CL-DiffPhyCon 理论分析

论文还从理论上分析了为何需要学习以上两个扩散模型。论文的目标是对联合分布进行建模，并在控制目标的引导下采样。本文将如下的增广 (augmented) 联合分布作为分析的出发点：

如果我们能够采样这个增广联合分布中的所有随机变量，那么自然也就得到了（包含于）。而之所以要研究这个增广联合分布，是因为它指引着我们让变得 “可被采样”。论文研究发现，这个看似复杂的增广联合分布其实具有一个有趣的规律：假设联合分布满足 Markov 性质（这是强化学习等决策类问题中常见的假设），那么从增广联合分布中采样的问题，就可以转化为只从两类分布中采样的问题：即先从一个初始分布中采样得到，再从一个转移分布中依次采样，得到一系列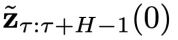（）。具体地，该采样过程可以用如下定理描述：

所以，这里采用了 “先繁再简” 的分析策略，为复杂的分布加入了采样的可行性。这个定理还传递出另一个重要的性质：在每个物理时刻采样控制变量时，所依赖的系统状态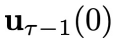可以从环境反馈中得到。这是因为我们已经采样得到了上一个时刻的控制变量，因此可以立即将其输入到环境中，得到环境反馈的。也就是说，这个采样过程能够满足闭环控制的要求。

仔细观察就会发现，上一节中学习的两个扩散模型恰好对应两个分布：即同步扩散模型的作用是从中采样，而异步扩散模型的作用是从中采样。所以，我们只需要这两个扩散模型就能够实现从轨迹数据分布中采样，再通过在采样过程中加入控制目标的梯度引导，就可以优化控制目标。

五、实验结果

1. 实验设置

借鉴 DiffPhyCon [1] 论文中的实验设置，这篇论文在两个具有挑战性的控制任务上进行了实验：

（1）一维 Burgers 方程控制：通过控制外力项，使系统的最终状态与目标状态一致。

（2）二维烟雾间接控制：通过间接控制外部力场，最小化从非目标出口逸出的污染物比例。

在一维 Burgers 方程控制实验中，考虑了 6 种实际场景，如无噪声控制、物理约束下的控制、存在系统和测量噪声时的控制，以及部分区域可控制（包括全部区域可观测和部分区域可观测两种细分场景）等。在二维烟雾间接控制任务中，设置了大范围区域控制和边界控制 2 种场景，每种又细分为固定障碍物地图和随机障碍物地图两种环境模式，以检验方法的泛化能力。

对比方法包括一系列经典控制方法、模仿学习、强化学习和扩散控制方法，如 PID、行为克隆（BC）、BPPO、自适应重规划扩散控制（RDM）以及 DiffPhyCon 等，并对这些基线方法进行了适当调整，以保证公平比较。由于两个实验中的轨迹较长，研究人员将 DiffPhyCon 扩展为三个版本：DiffPhyCon-h（h∈{1,5,H - 1}）。这里的 DiffPhyCon - h表示每隔h个物理时间步进行一次 DiffPhyCon 的完整采样过程，然后将采样的控制信号序列中的前h个用于开环控制（见上文图 1）。

2. 实验结果

在一维 Burgers’方程控制任务中，CL–DiffPhyCon 在 6 种场景下控制效果均优于所有对比方法。与控制效果最佳的对比方法 DiffPhyCon-1 相比，CL-DiffPhyCon 在无噪声和带有物理约束的设置中，使控制目标分别降低了 54.3% 和 48.6%；在两种噪声的情况下，控制目标分别降低了 48.6% 和 57.2%；在部分区域可控制场景中，控制目标分别降低了 11.8% 和 11.1%。在采样效率上，CL-DiffPhyCon 相比每个 DiffPhyCon-h 快了约 H/h 倍（h∈{1,5,15}），也比自适应重规划扩散控制（RDM [4]）快两倍。结合 DDIM 采样后，加速效果更明显，进一步实现了 5 倍的加速，且控制效果保持相当。

表 1. 一维 Burgers’方程控制任务上的实验结果对比。

在二维烟雾间接控制中，CL-DiffPhyCon 同样表现优异，在 4 种场景设置中，效果均优于对比方法。在采样效率方面，CL-DiffPhyCon 比 DiffPhyCon-h 实现了约 H/h h∈{1,5,14} 倍的加速，并且比 RDM 更高效。结合 DDIM 后，推理速度进一步加快，比 RDM 快 5 倍以上。

表 2. 二维烟雾间接控制任务上的实验结果对比。

图 3. 在固定地图（上图）和随机地图（下图）两种环境下，CL-DiffPhyCon 与表现最好的对比方法在二维烟雾间接控制上的可视化对比。横向表示不同物理时刻。控制目标 J 越低，表示控制效果越好。

六、总结与展望

CL-DiffPhyCon 为高效闭环控制提供了一种创新解决方案。通过实验验证，证明了其具有兼得优良的控制效果和高效的采样效率的显著优势。不过，研究人员也指出，该方法仍有提升空间。目前 CL-DiffPhyCon 是基于离线数据训练的，未来可以考虑在训练过程中融入环境实时反馈，探索多样的控制策略。此外，虽然两个扩散模型是基于对目标分布的理论分析推出，但在引导采样下得到的样本与最优解的误差界仍是一个开放问题，值得进一步深入研究。

从应用前景来看，CL-DiffPhyCon 不仅适用于这篇论文的复杂物理系统控制任务，在机器人控制、无人机控制等领域也具有广阔的应用潜力。随着研究的不断深入和技术的持续进步，CL-DiffPhyCon 将不断完善，为更广泛领域的控制问题提供有益的解决方案。