一直以来，研究者普遍认为，去噪扩散模型要想成功运行，噪声条件是必不可少的。
而大神何恺明的一项最新研究，对这个观点提出了「质疑」。
「受图像盲去噪研究的启发，我们研究了各种基于去噪的生成模型在没有噪声调节的情况下的表现。出乎我们意料的是，大多数模型都表现出了优美的退化，它们甚至在没有噪声条件的情况下表现得更好。」
- 论文标题：Is Noise Conditioning Necessary for Denoising Generative Models?
- 论文地址：https://arxiv.org/pdf/2502.13129
研究者对这些模型在无噪声条件情况下的行为进行了理论分析。具体来说，他们研究了噪声水平分布中固有的不确定性、在没有噪声条件的情况下去噪所造成的误差以及迭代采样器中的累积误差。综合这些因素，提出了一个误差边界，该误差边界的计算无需任何训练，完全取决于噪声条件和数据集。
实验表明，这个误差边界与所研究的模型的噪声 - 无条件行为有很好的相关性，特别是在模型出现灾难性失败的情况下，其误差边界要高出几个数量级。
由于噪声 - 无条件模型很少被考虑，专门为这种未充分探索的情况设计模型是有价值的。为此，研究者从 EDM 模型中提出了一个简单的替代方案。在没有噪声条件的情况下，该变体可以实现很强的性能，在 CIFAR10 数据集上的 FID 得分达到 2.23。这一结果大大缩小了噪声 - 无条件系统与噪声 - 条件系统之间的差距（例如，EDM 的 FID 为 1.97）。
关于未来，研究者希望消除噪声条件将为基于去噪的生成模型的新进展铺平道路，激励业界重新审视相关方法的基本原理，并探索去噪生成模型领域的新方向。例如，只有在没有噪声条件的情况下，基于分数的模型才能学习到独特的分数函数，并实现经典的、基于物理学的朗格文动力学。
对于这项新研究，有人评论称：我们花了数年时间来完善噪声条件技术，到头来却发现即使没有噪声条件，模型同样能运行得很好。所以，科学其实就是利用额外数学的反复试错。
去噪生成模型的重构
研究者提出了一种可以总结各种去噪生成模型训练和采样过程的重构（reformulation），核心动机是隔离神经网络 NN_θ，从而专注于其在噪声条件方面的行为。
首先来看去噪生成模型的训练目标。在训练期间，从数据分布 p (x) 中采样一个数据点 x，并从噪声分布 p (ϵ)（例如正态分布 N (0, I)）中采样噪声 ϵ。噪声图像 z 由以下公式得出：
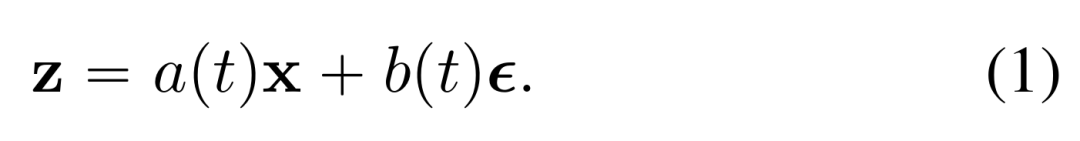
一般来说，去噪生成模型涉及最小化损失函数，该函数可以写成：
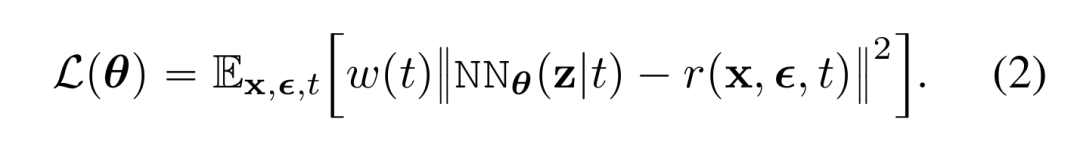
现有几种方法（iDDPM、DDIM、EDM 和 FM）的调度函数具体如下表 1 所示。值得注意的是，在研究者的重构中，他们关注的是回归目标 r 与神经网络 NN_θ 直接输出之间的关系。
其次是采样。给定训练好的 NN_θ，采样器迭代地进行去噪。具体来讲，对于初始噪声 x_0 ～ N (0, b (t_max)^2I)，采样器迭代地计算如下：
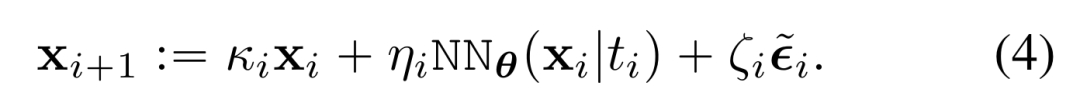
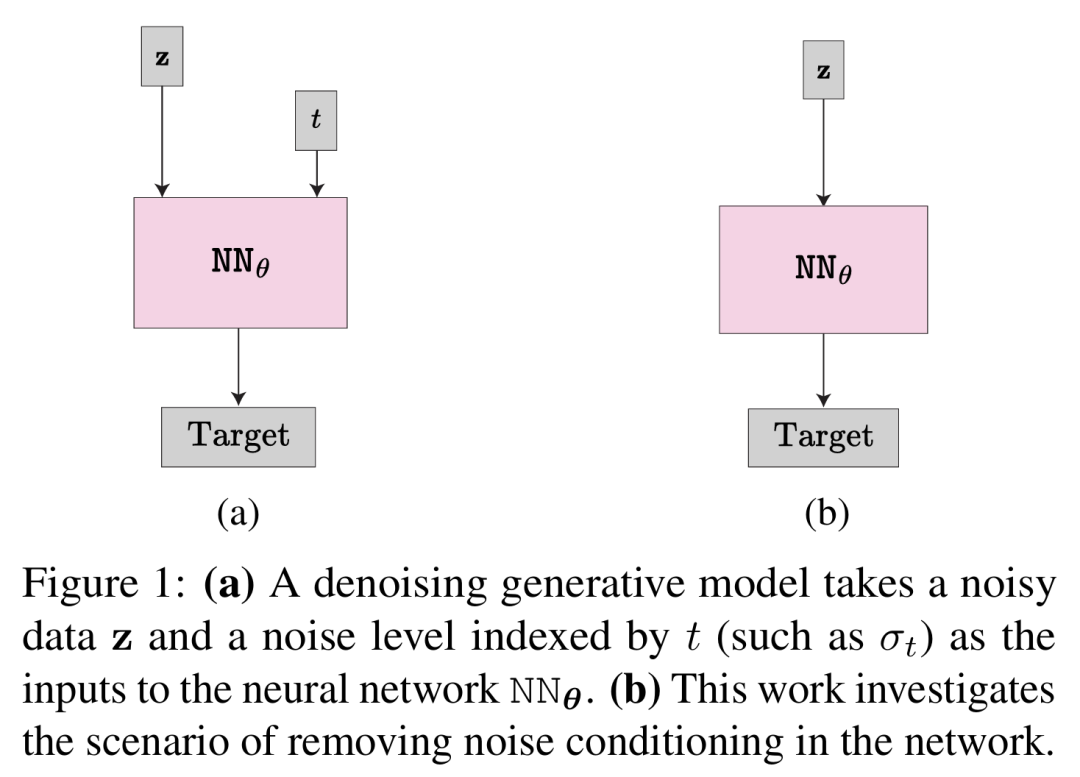
最后是噪声条件网络。在现有方法中，神经网络 NN_θ(z|t) 以 t 指定的噪声水平为条件，具体可以参见图 1（左）。
同时，t-embedding 提供时间级信息作为网络额外输入。本文的研究涉及这种噪声条件的影响，即考虑了 NN_θ(z) 和 NN_θ(z|t)，参见图 1（右）。
无噪声条件模型
基于上述重构，研究者对消除噪声条件的影响进行了理论分析，其中涉及到了训练目标和采样过程。他们首先分析了训练阶段的有效回归目标和单个去噪步骤中的误差，然后给出了迭代采样器中累积误差的上限。
有效目标
形式上，优化公式 (2) 中的损失等同于优化以下损失，其中预期 E [・] 中的每个项都有对应的唯一有效目标：
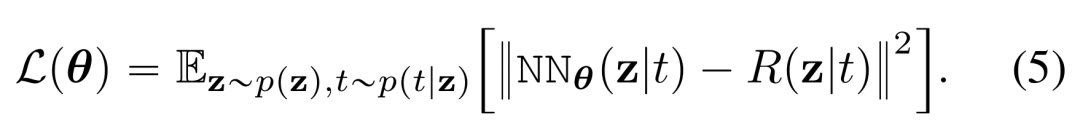
对于无噪声条件的有效目标，同样地，如果网络 NN_θ(z) 不接受 t 作为条件，则其唯一的有效目标 R (z) 应该仅取决于Z。在这种情况下，损失为：
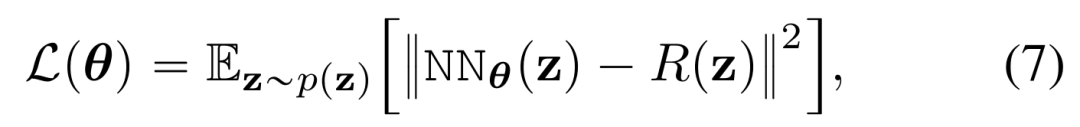
唯一有效目标如下：
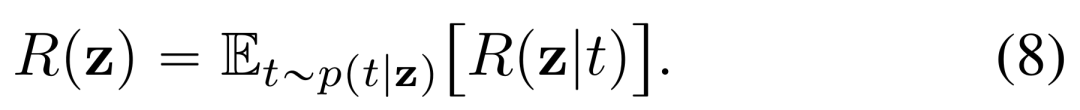
后验集中 p (t|z)
接下来，研究者探究了 p (t|z) 与狄拉克 δ 函数的相似度。对于图像等高维数据，人们早已意识到可以可靠地对噪声水平进行估计，这意味着可以得到一个集中的 p (t|z)。
陈述 1：（p (t|z) 集中）。考虑单个数据点 x ϵ [-1, 1]^d，则 ϵ～(0, I)，t～U [-0, 1] 以及 z = (1 - t) x + tϵ（流匹配情况）。给定一个由已有 t_⁎生成的噪声图像 z = (1 - t_⁎) x + t_⁎ϵ，条件分布 p (t|z) 下 t 的方差如下：
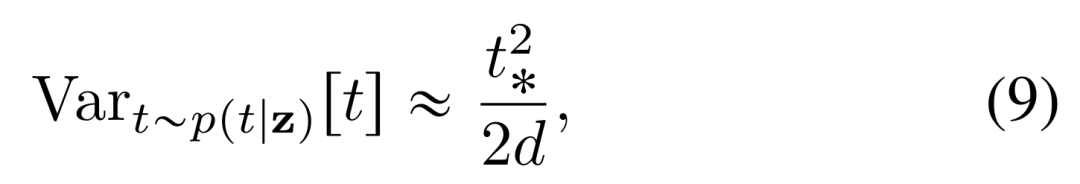
有效回归目标的误差
使用 p (t|z)，研究者探究了有效回归目标 R (z) 和 R (z|t) 之间的误差。在形式上，考虑如下：
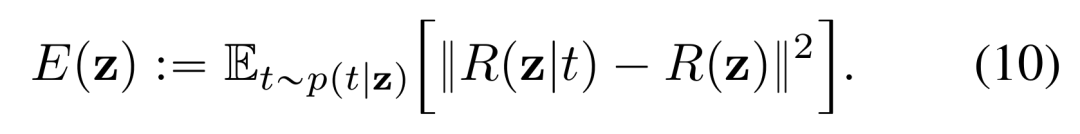
他们表明，方差 E (z) 明显小于 R (z) 的范数。
陈述 2（有效回归目标的误差）。考虑到陈述 1 中的场景以及流匹配情况，公式 (10) 中定义的误差满足如下：
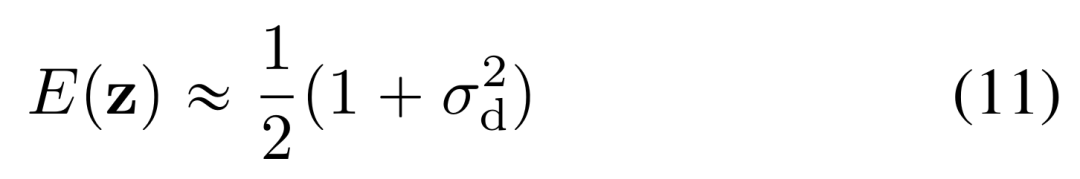
采样中的累积误差
到目前为止，研究者关注到了单个回归步骤的误差。而在去噪生成模型中，推理采样器是迭代的，因而进一步研究了迭代采样器中的累积误差。
为了便于分析，研究者假设网络 NN_θ 足以拟合有效回归目标 R (z|t) 或 R (z)。在此假设下，他们将上面公式 (4) 中的 NN_θ 替换为 R。这就有了以下陈述 3：
陈述 3（累积误差的上限）。考虑公式 (4) 中 N 个步骤的采样过程，从相同的初始噪声 x_0 = x’_0 开始。通过噪声调节，采样器计算如下：
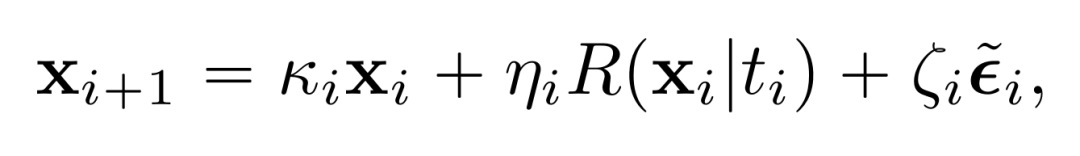
而在无噪声条件下，计算如下：
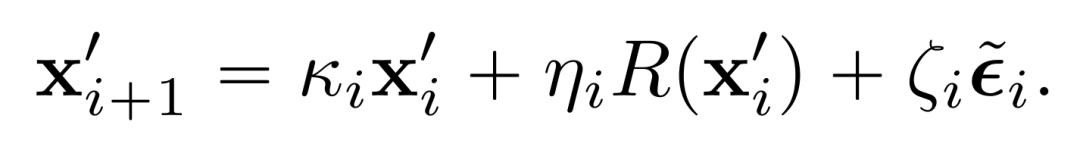
作为参考，EDM 设置为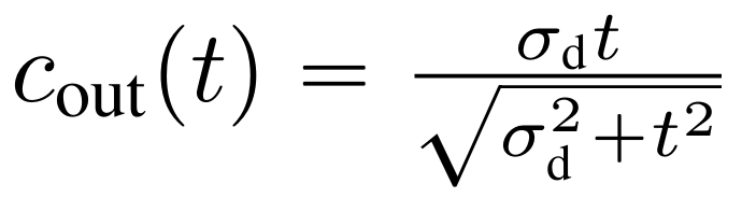
，其中 σ_d 为数据标准差。由于
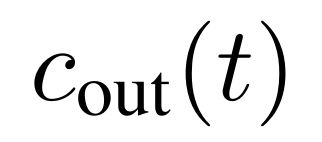是应用于网络 NN_θ 的系数，因而研究者将其设置为常数以使该网络不用建模一个 t - 依赖尺度。在实验中，这种简单的设计表现出了比 EDM 更低的误差上限（陈述 3），因而被命名为了 uEDM，它是无噪声条件的缩写。
实验结果
研究者对各种模型的噪声条件影响进行了实证评估：
- 扩散：iDDPM、ADM、uEDM
- 基于流的模型：此处采用了 Rectified Flow (1-RF)
- 一致性模型：iCT ECM
下表 2 总结了不同生成模型中的 FID 变化情况，有或无噪声调节分别用 “w/t ” 和 “w/o t ” 表示。
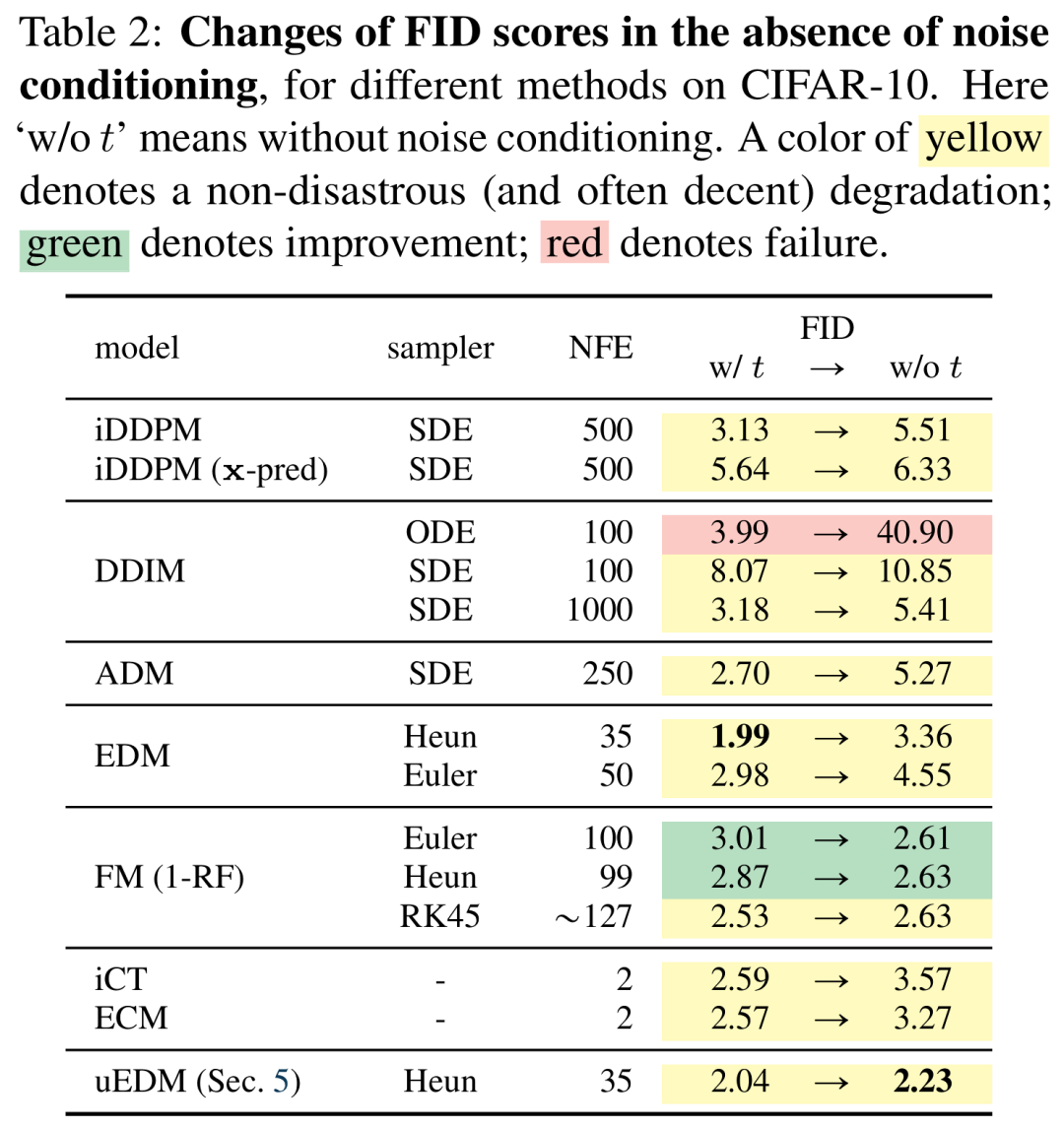
划重点如下：
(i) 与通常的看法相反，噪声条件并不是大多数基于去噪模型发挥作用的有利因素。大多数变体都能优雅地工作，表现出微小但适当的衰减（黄色）；
(ii) 在去除噪声条件后，一些基于流的变体可以获得更好的 FID（绿色）；
(ili) uEDM 变体在不使用噪声条件的情况下实现了 2.23 的 FID，缩小了与噪声条件方法的强基线的差距；
(iv) 与扩散模型相关但目标函数有很大不同的一致性模型，也可以表现得很优美；
(v) 在本文研究的所有变体中，只有「DDIM w/ ODEsampler*」会导致灾难性失败（红色），FID 显著恶化至 40.90。图 5 (a) 展示了其定性表现：模型仍然能够理解形状和结构，但 「overshoot」或「undershoot」会产生过饱和或噪声结果。
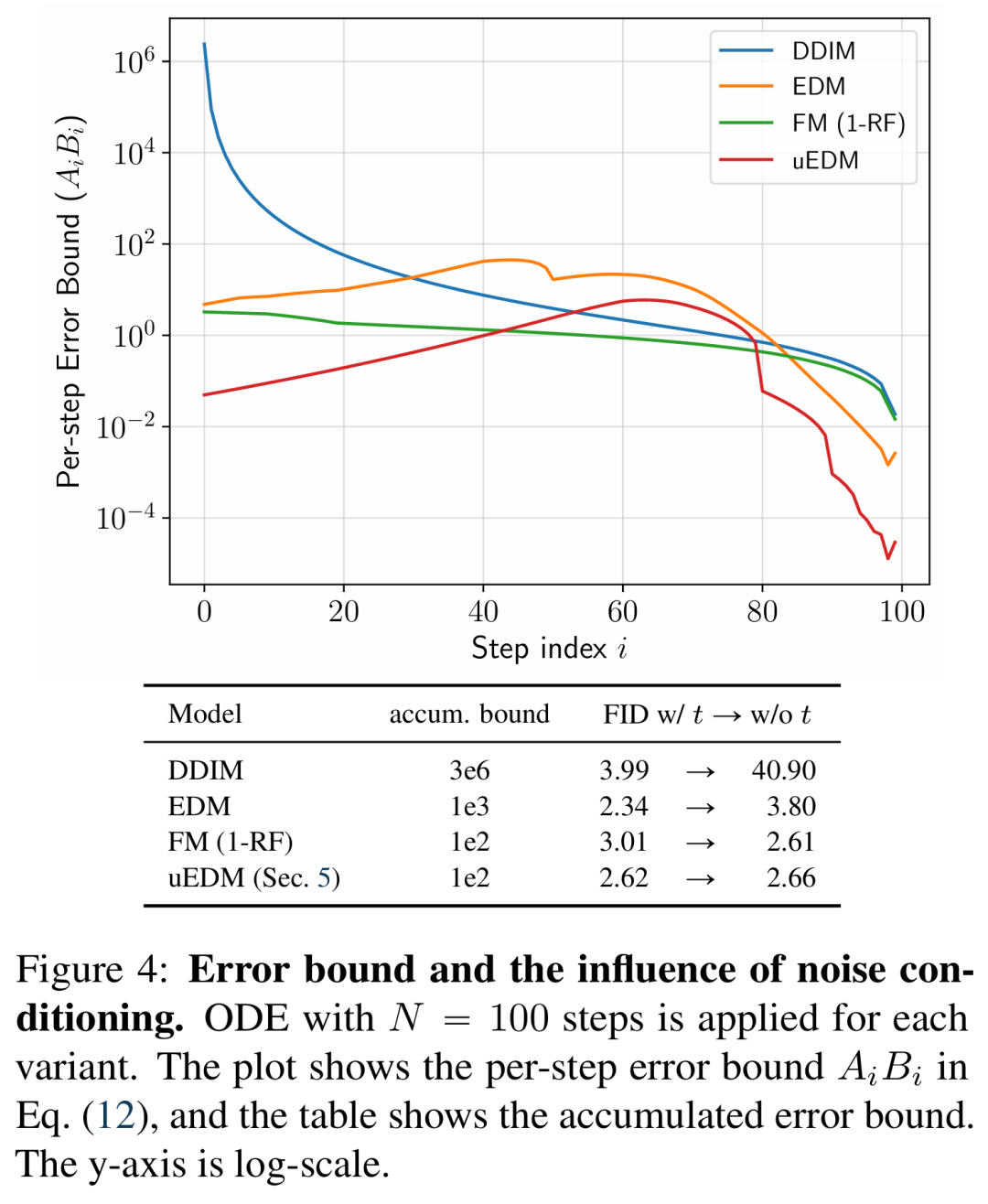
在图 4 中，研究者根据经验评估了在 100 步 ODE 采样器下不同方法的陈述 3 中的误差边界。误差边界的计算只取决于每种方法的时间表和数据集。图 4 也展示了理论边界与经验行为之间的紧密联系。具体来说，DDIM 的灾难性失败可以用其误差边界高出几个数量级来解释。另一方面，EDMFM 和 uEDM 在整个过程中的误差边界都很小。
随机性水平。在表 2 中，DDIM 只在确定性 ODE 采样器中失败；在 SDE 采样器（即 DDPM 采样器）中仍然表现良好。
如图 6 所示，随机性越大，FID 分数越高。当 λ=1 时，DDIM 的表现与 iDDP 类似。
