臭名昭著的「搬沙发」难题，已经困扰了数学家们60年。
《老友记》经典的一幕，就是Ross找人帮忙搬新沙发时，无论如何也无法使沙发顺利通过拐角。
Ross大喊「Pivot！Pivot！」，意即绕着某个中心轴转动
「搬沙发」难题之所以如此棘手，就在于它要求在几何学上满足最大形状在狭窄走廊中转动一个直角而不被卡住。
能顺利通过L形走廊的最大沙发形状和尺寸是什么？这个问题，难倒了数学家们60年。
在流行数学论坛Mathoverflow上，「任何人都能理解的并不著名长期数学问题」排行榜中，这个难题长期排名第二
如今，这个难题一朝破解！
移动沙发难题，数学家探索了60年
1966年，加拿大数学家Leo Moser将「移动沙发难题」以定量的形式提出——
假设要移动一个二维形状（忽略沙发高度）通过宽度为1单位的L形走廊，那么这个不会被卡住的最大形状的面积是多少呢？
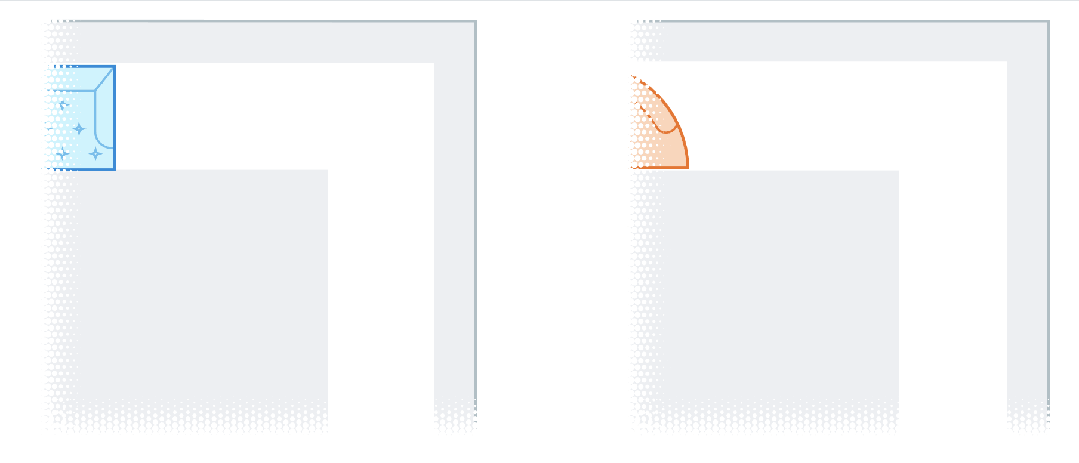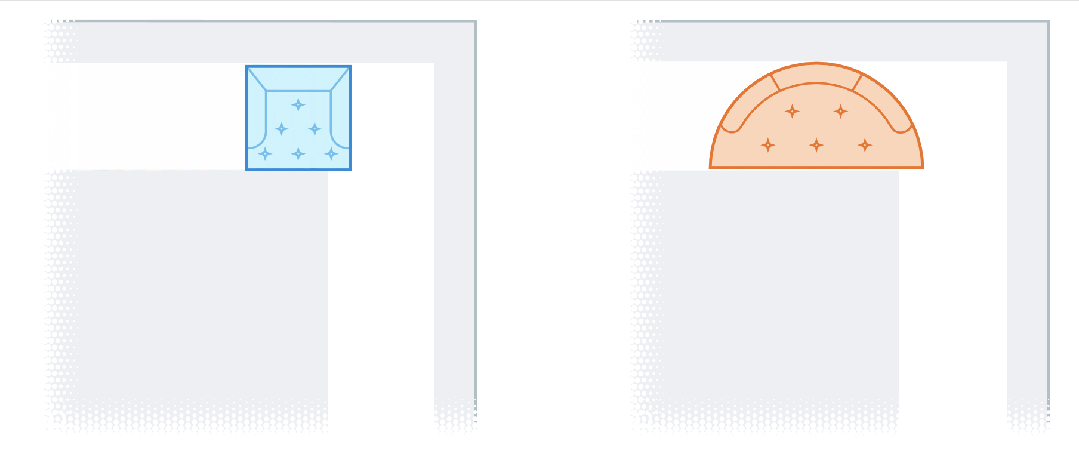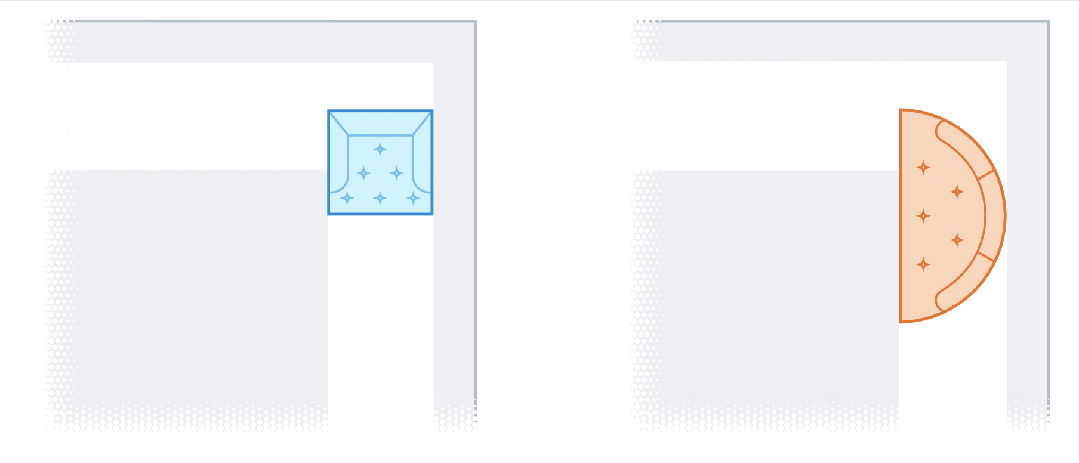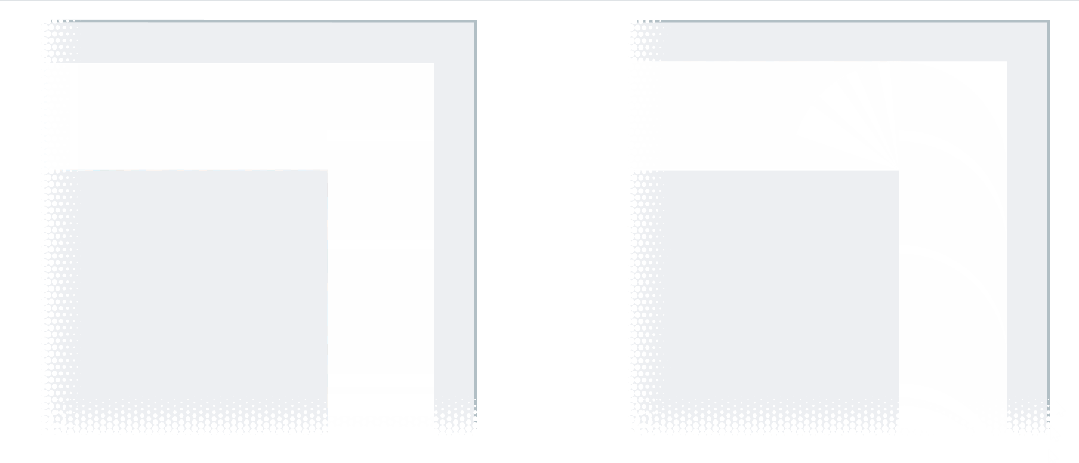
起初，人们很容易想到一些能通过转角的简单形状。比如边长为1的正方形，能顺利通过转角，面积为1。
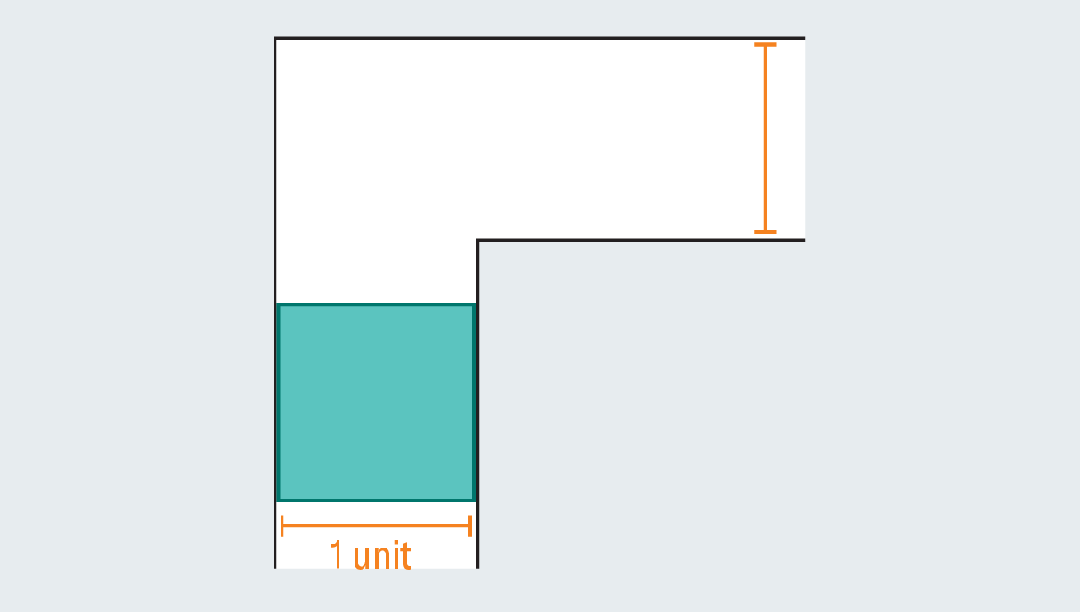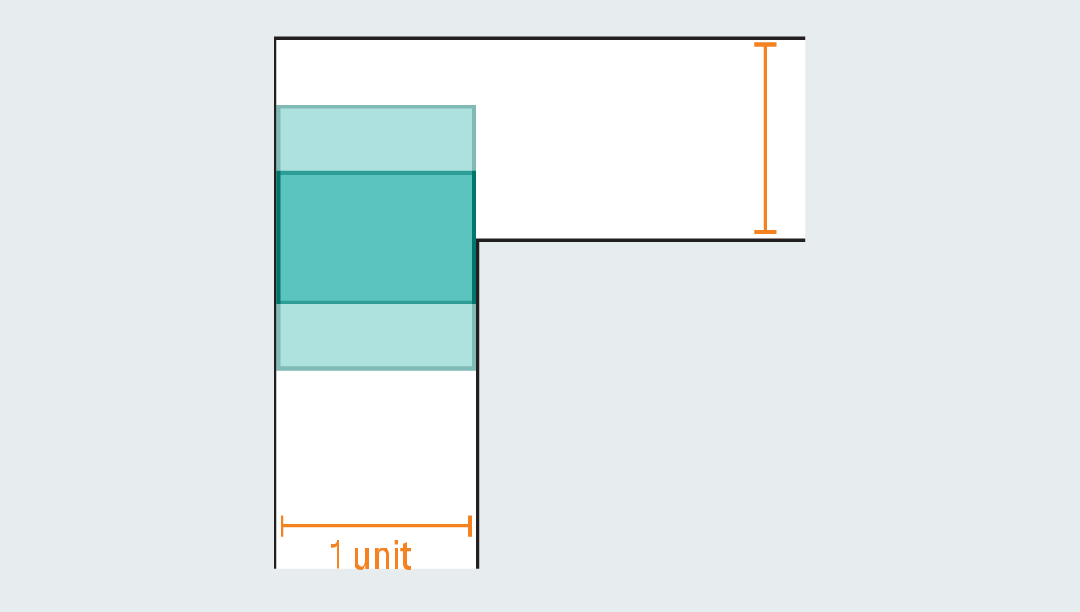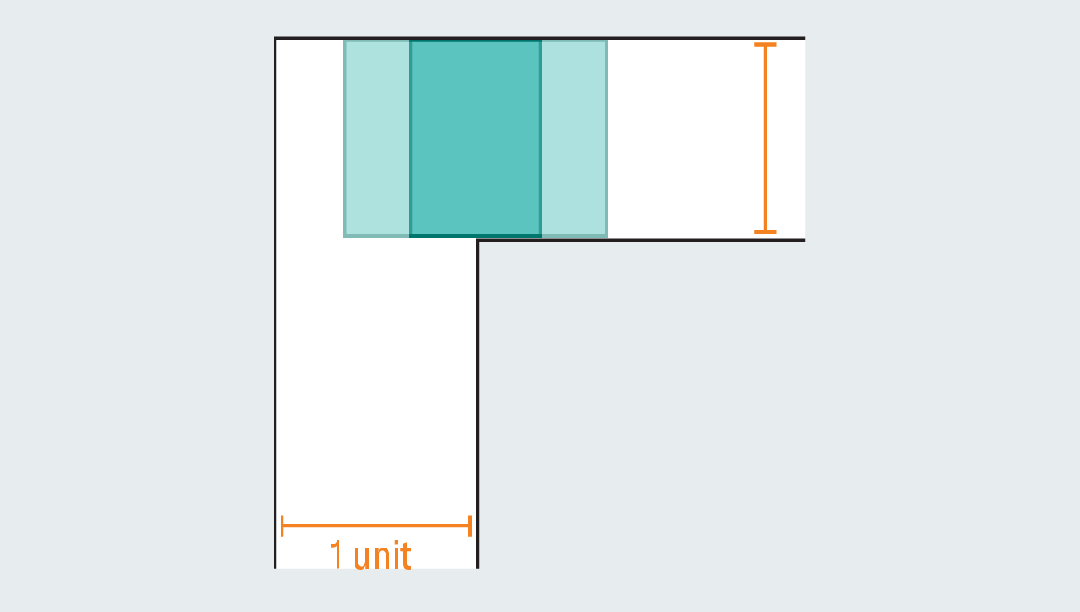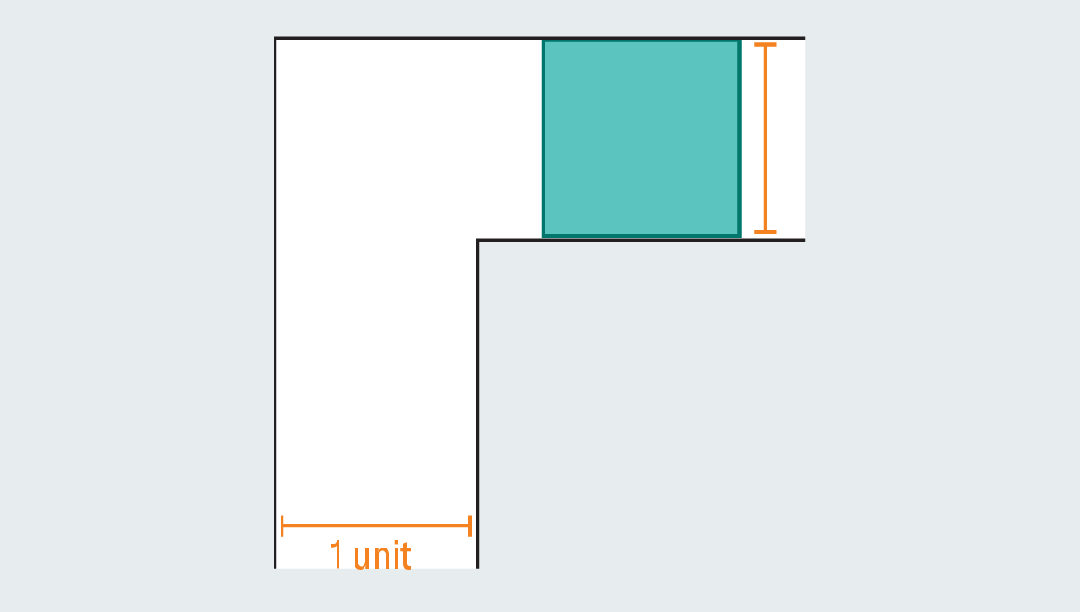
然而，一旦正方形伸长成矩形，就会立刻失效，撞上走廊。
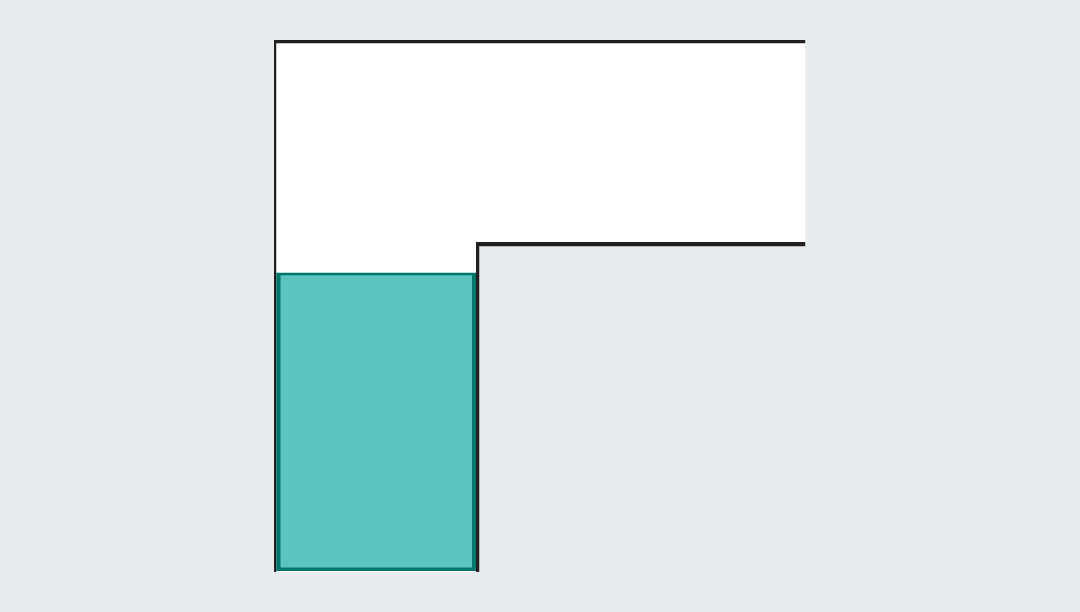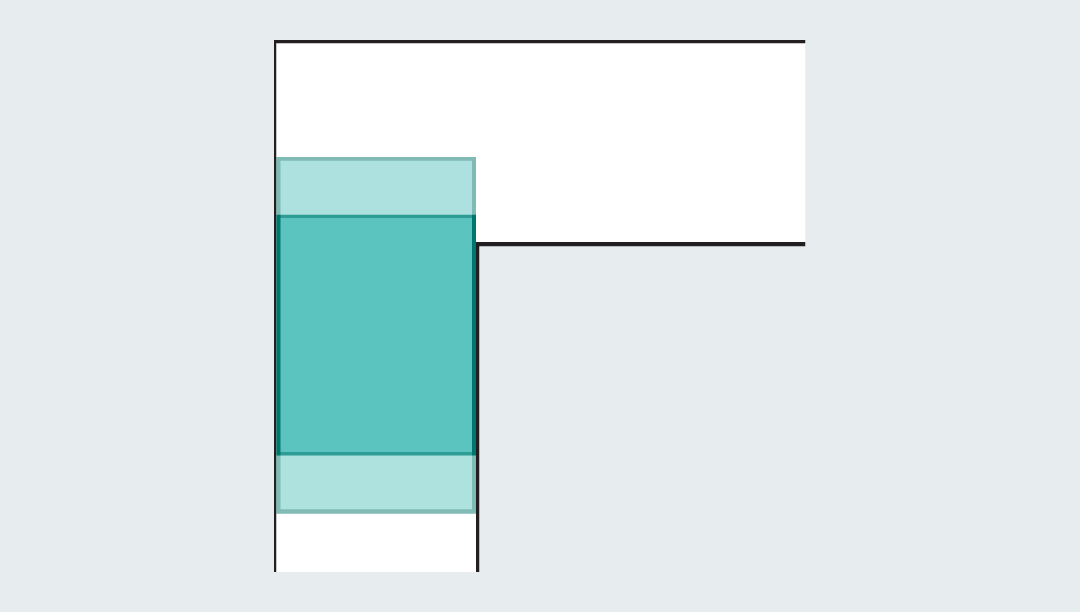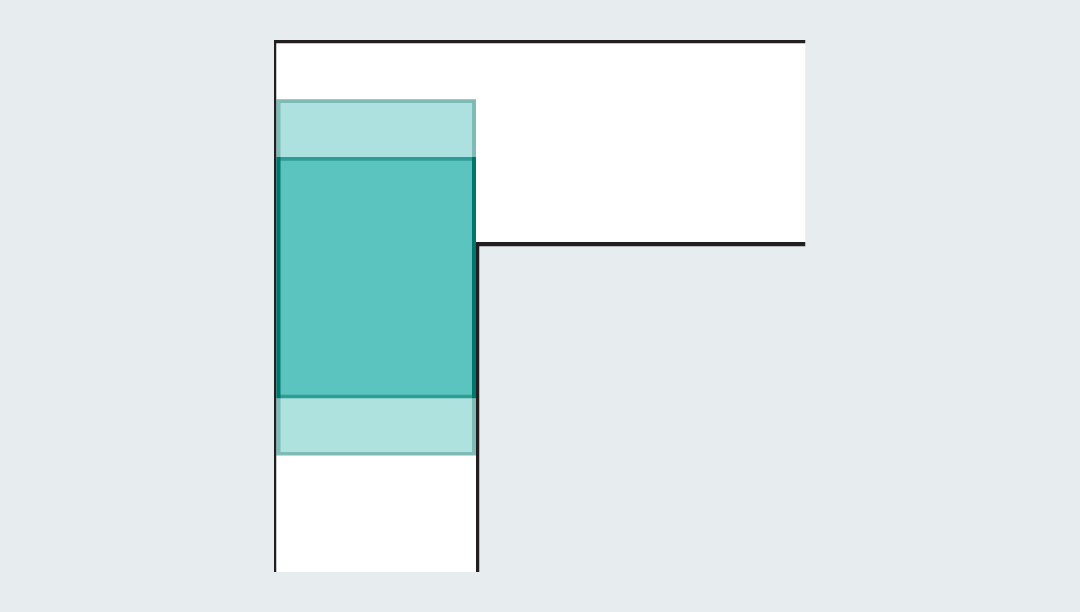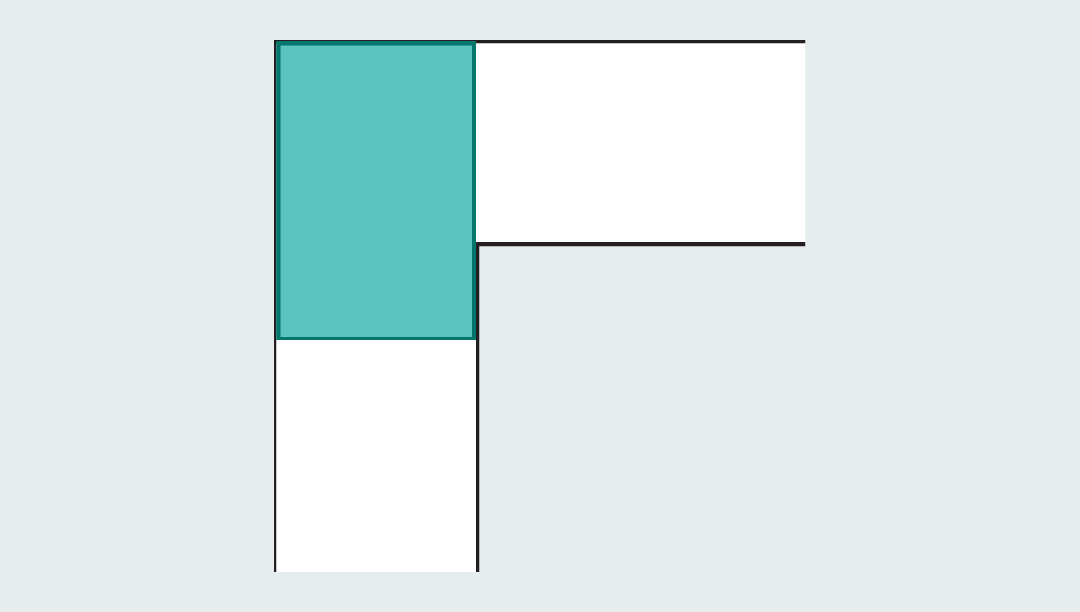
数学家们想到：既然如此，就可以通过引入完全的形状，来扩大面积！
比如一个半径为1的半圆，面积约为1.57（π/2），当它撞到拐弯处时，圆形的边缘就留下了足够的空间，来通过角落。
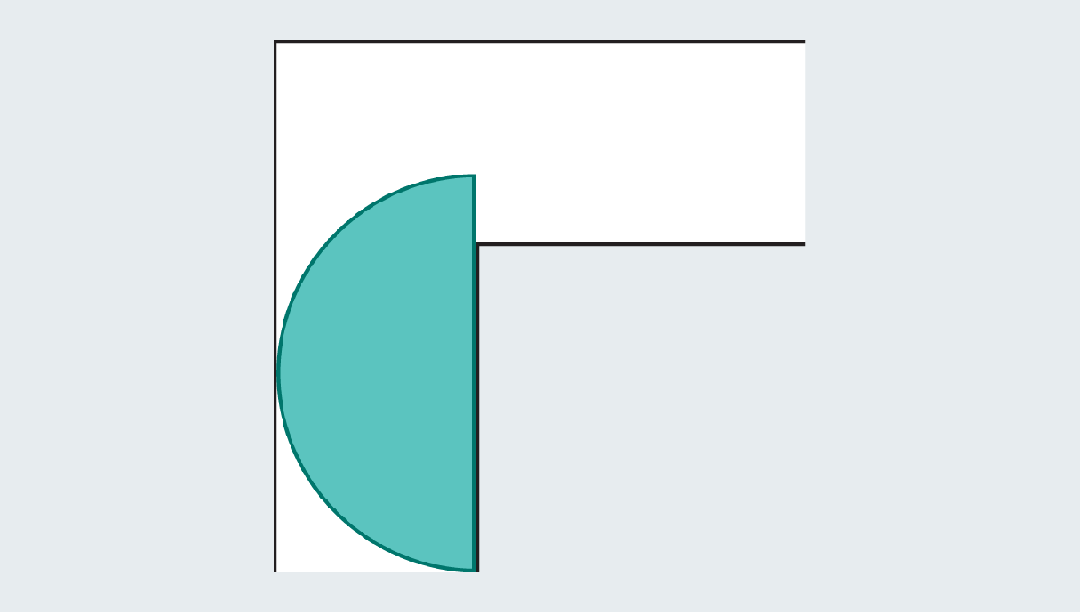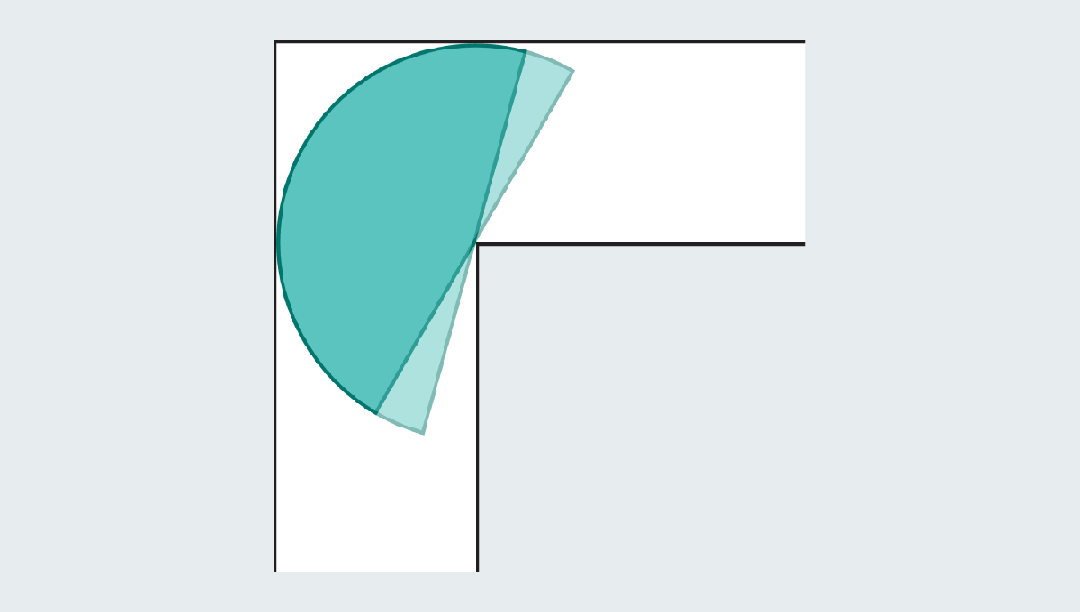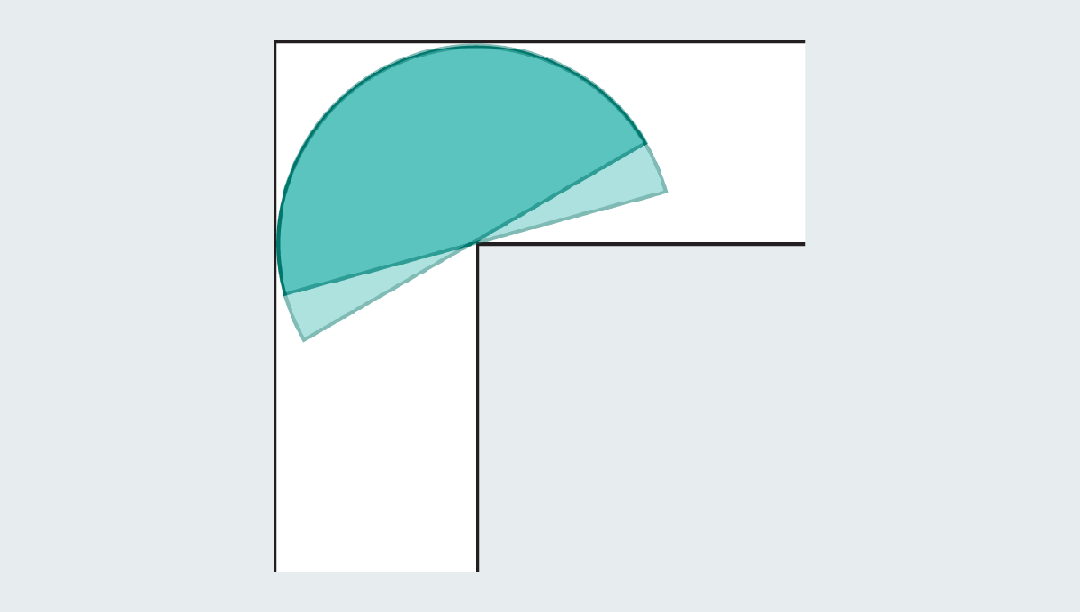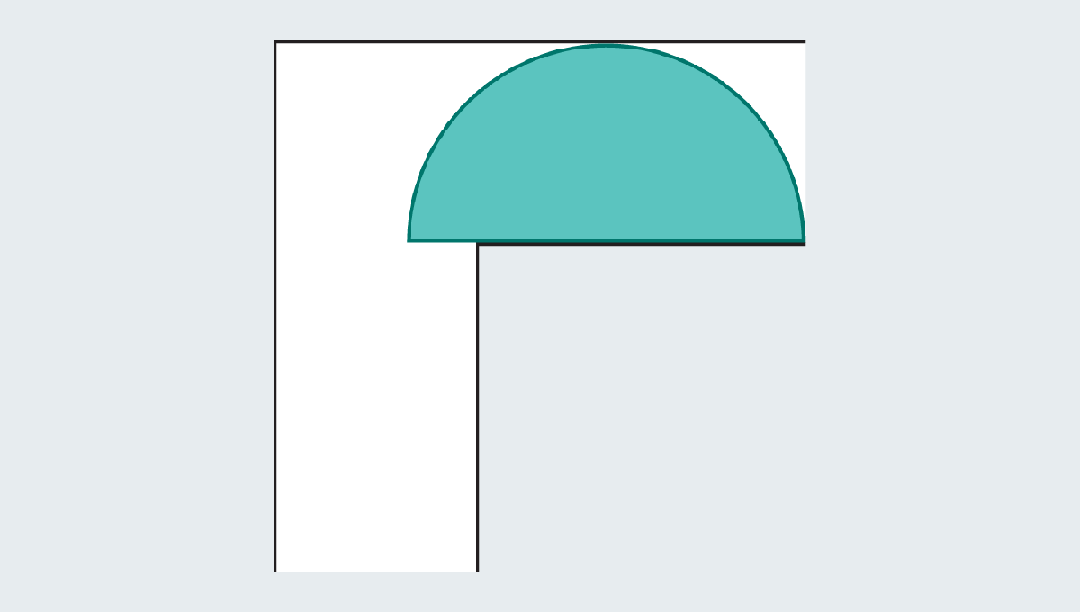
但是，这些形状的面积仍然不够大！显然不是数学家们追求的最优解。一定还有面积更大、更巧妙的形状。
问题关键就在于，既要优化形状大小，还要优化穿越路径。也就是说，有两种类型的运动：滑动和旋转。
而解决问题的关键，就在于同时优化两种类型的运动。
1968年，英国数学家John Hammersley发现：可以抠出一大块，来应对那个讨厌的角落，同时延伸半圆形，让我们的沙发面积更大（面积为 π/2 + 2/π, 大约2.2074）。
这种形状像座机电话的沙发，就混合了滑动和旋转运动的优势。
自从这个半圆形变为电话形的重大升级后，这个问题一停滞就是24年！
1992年，罗格斯大学的Joseph Gerver提出了一种巧妙的形状，面积约为2.2195，它似乎是目前已知最大的沙发。
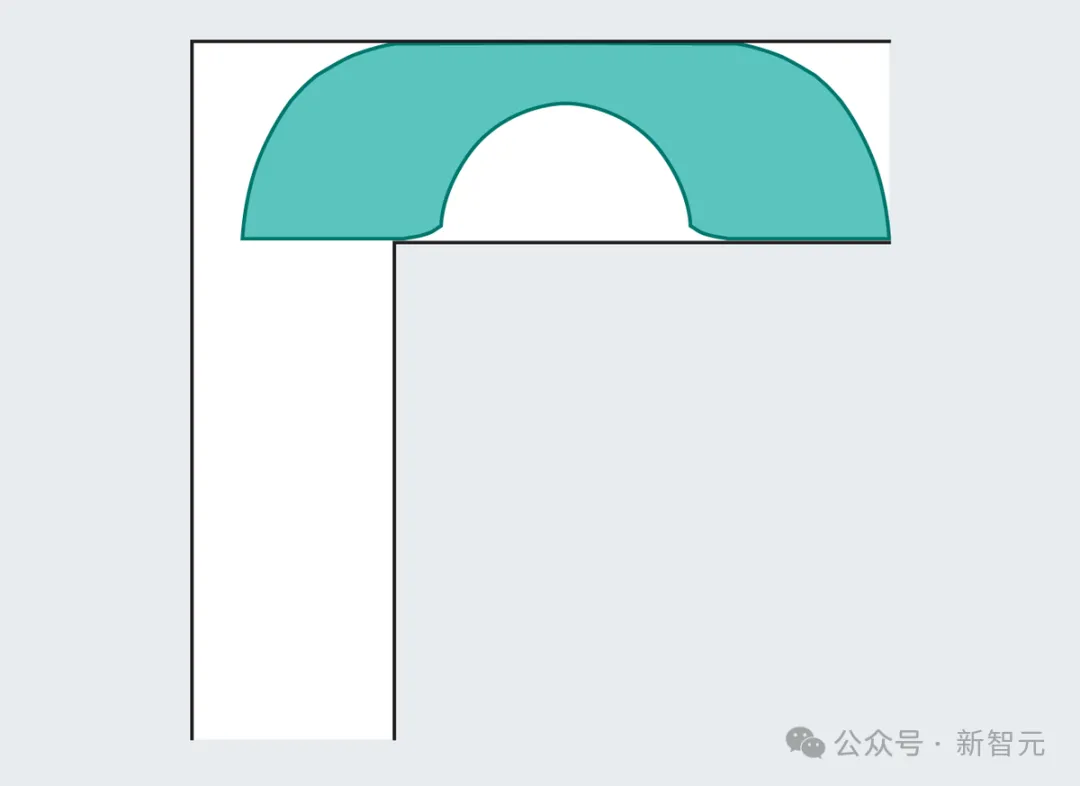
看起来， Gerver的沙发看起来与Hammersley的沙发大差不差。
不过仔细看的话，会发现一些细微的差异：在这个新图里，Gerver缝合了18个不同的形状，在圆形切口底部的斜角边缘，跟Hammersley的沙发有一些差别。
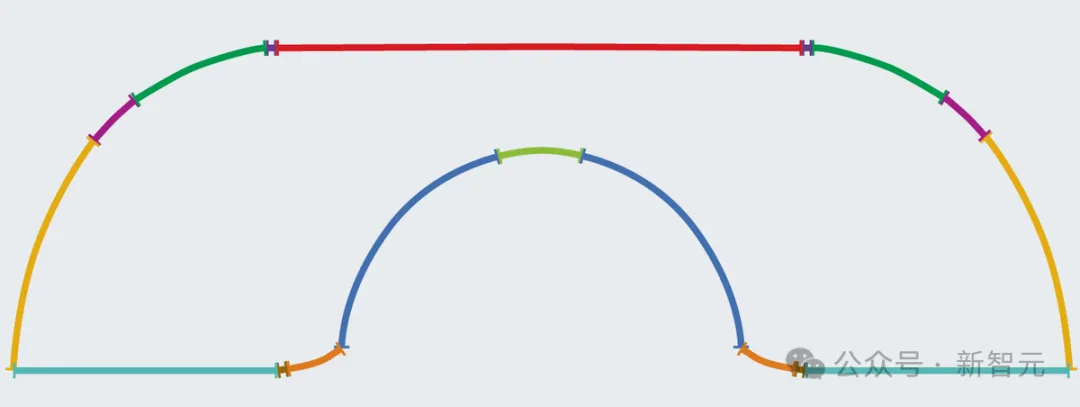
Gerver怀疑，自己找到了最大可能的大小，但无法自证。
数学家们也怀疑它就是Moser问题的答案，但一直无法证明。
如今，这个数学世界难题终于有解了！
一位年轻的博士后研究员——首尔延世大学的Jineon Baek在一篇长达119页的论文中证明，Gerver设计的沙发就是能够顺利通过拐角的最大形状！
论文地址：https://arxiv.org/pdf/2411.19826
60年难题得解，数学界轰动了。
此前，数学家们普遍认为，要证明这个猜想可能需要计算机，而Baek的证明完全没有使用计算机。
更有趣的是，Gerver的沙发与常见的几何形状不同，它的面积无法用已知的数学量（如π或平方根）来表示。
然而，在「移动沙发问题」这个看似简单的问题中，它却是最优解。
沙发与电话
说起来，Gerver最开始得知这个问题，就是从John Hammersley那里。
后者将两个四分之一圆与一个矩形相连，然后从中切出一个半圆，创造出了一个类似老式电话的形状。这个形状的面积约为2.2074（π/2+2/π）。
Hammersley还证明了这个问题的任何解，面积最大不会超过约2.8284（
）。
几年后，当时还是加州大学伯克利分校研究生的Gerver得知了这个问题。
在接下来的20年里，Gerver一直在断断续续思考这个问题。
直到1990年，他向著名数学家John Conway提及此事，才发现它是一个未解之谜。
这激发了他的斗志，不久后，他就提出了一个极具潜力的方案。
Gerver的沙发形状比Hammersley的更复杂，由18个不同部分组成。有些部分是简单的线段和弧线，有些则更加奇特。
尽管形状复杂，但Gerver怀疑它就是最优解：它具有数学家期望的许多特征，这是最佳沙发所拥有的特质。
他证明了对其轮廓进行小的改变，并不会得到面积更大的合适形状。
后来他还发现，贝尔实验室的工程师Ben Logan也独立发现了相同的形状，但从未发表。
2016年，加州大学戴维斯分校的数学家Dan Romik对Gerver的沙发给出了更具概念性的描述。
他写下了一组包含22个变量的22个方程，这组方程的唯一解在绘图时就是Gerver发现的类似电话的形状。
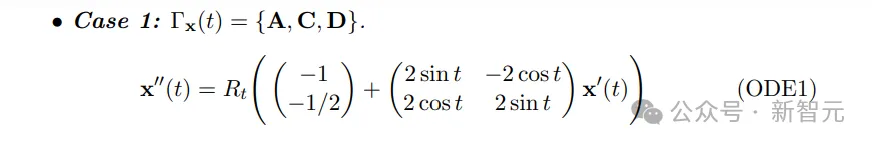
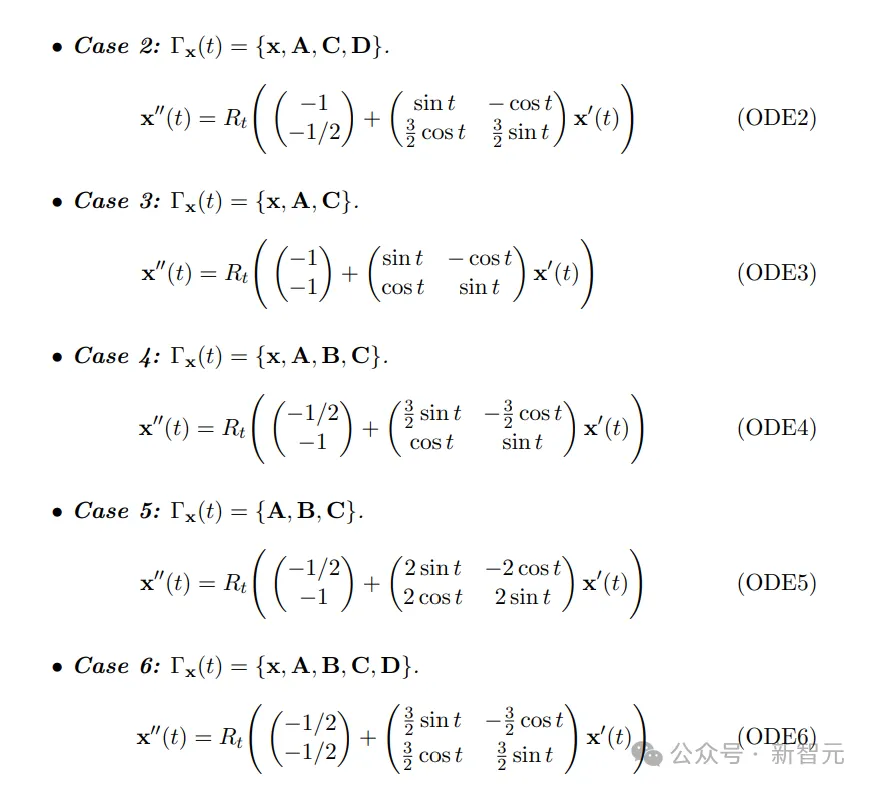
次年，Romik和Yoav Kallus利用计算机辅助技术缩小了Hammersley给出的面积上限与Gerver形状面积之间的差距，但仍未完全解决问题。
年轻博士后攻克难关
在探索这个问题的征程中，韩国延世大学的博士后Jineon Baek脱颖而出。
2016年，刚进入密歇根大学攻读研究生的Baek因服兵役中断学业。在服役期间，他在一篇博客文章中看到了「移动沙发问题」。
起初，他只是把它当作工作之余放松的方式，但很快就认真起来。
他有一个初步想法，能证明Gerver的沙发是正确答案，但还有许多细节需要完善。2021年回到学校后，他决心攻克这个难题。
通常情况下，数学博士生会选择导师，然后由导师分配研究问题。
但Baek一心想研究「移动沙发问题」，这使得他在寻找导师时遇到了困难，因为密歇根大学的教授们觉得自己在这个领域缺乏足够的专业知识。
幸运的是，代数领域的专家Michael Zieve同意指导他。Zieve表示：「我从未指导过与我研究领域相差这么远的学生，但我愿意尝试。」
这种跨领域的指导，为Baek的研究带来了新的视角和可能。
在攻读博士期间，Baek在Kallus和Romik的工作基础上继续深入研究。他开发了强大的计算工具，进一步缩小了面积上限，取得了重要的阶段性成果。
原本，Baek打算毕业后继续采用计算方法来彻底解决「移动沙发问题」。但几个月后，他意识到或许可以不依赖计算机来完成证明。
数学家们早已知道，任何满足「移动沙发问题」的解都需要具备特定条件。比如，最优沙发要能够以特定方式旋转，底部需要有为走廊转角留出空间的部分等等。
满足这些条件的形状有无穷多个，Baek首先做的是缩小范围，通过一系列复杂的数学推理证明，最优形状至少与Gerver的沙发相似。
他将每个沙发表示为无限维空间中的一个点。理想情况下，他希望找到一个函数，输入点就能输出沙发面积，进而找到函数输出最大时对应的点。
但由于不存在能计算所有形状面积的通用公式，他决定间接研究形状面积。Baek发明了一个新函数Q，并定义了它的几个重要属性。
首先，对于他所定义空间中的任何沙发，Q的输出至少和沙发面积一样大，它本质上测量的是包含沙发的一个形状的面积。这意味着如果能找到Q的最大值，就能得到最优沙发面积的一个上限。
更关键的是，对于Gerver的沙发，函数Q的输出恰好等于其面积。所以，Baek只需证明当输入为Gerver的沙发时，Q能取到最大值，就能证明Gerver的沙发是「移动沙发问题」的最优解。
Baek精心构建的Q函数表现很好，类似于简单的抛物线，相对容易找到最大值。他证明了使Q最大化得到的形状满足一组特定条件，而定义Gerver沙发的方程也满足这些条件。
就这样，他解决了这个困扰数学家们数十年的难题，证明了Gerver的沙发是能通过走廊且不被转角卡住的最大形状。
Baek的证明仍在同行评审中。他结合了数学不同领域的技术，让这个原本极其困难的问题变得可解，而且全程没有借助计算机。
Zieve评价道：「Baek能不借助计算机完成证明，令人印象深刻，这表明其中有重要的新想法。」
Gerver在提出方案30多年后，终于看到问题被解决，他感慨道：「我现在75岁了，能活着看到有人最终解决了这个问题，我觉得很幸运。」
论文简介
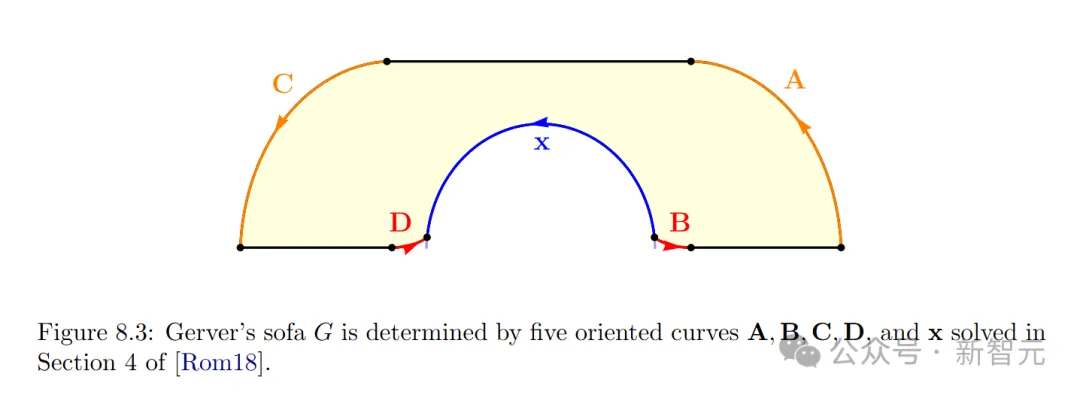
摘要：通过证明具有18个曲线段的Gerver沙发的确达到了最大面积2.2195，解决了移动沙发问题。
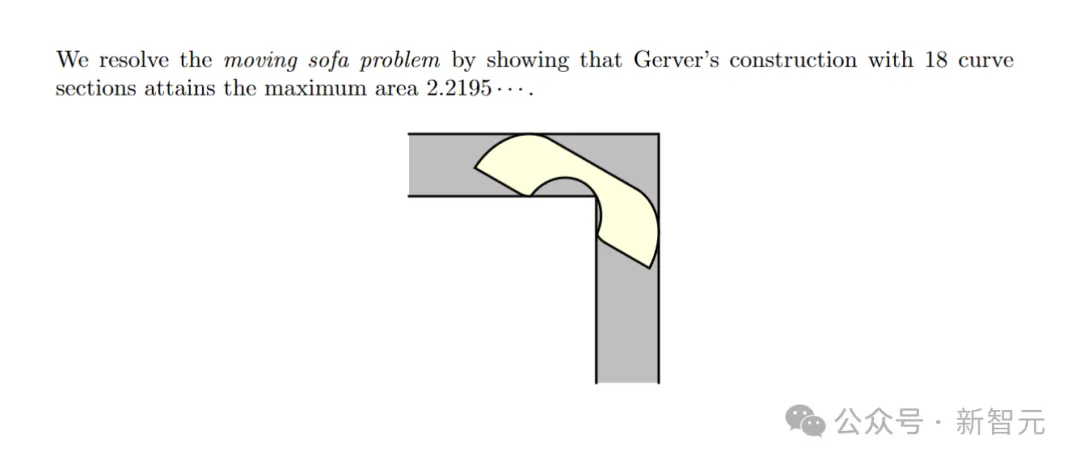
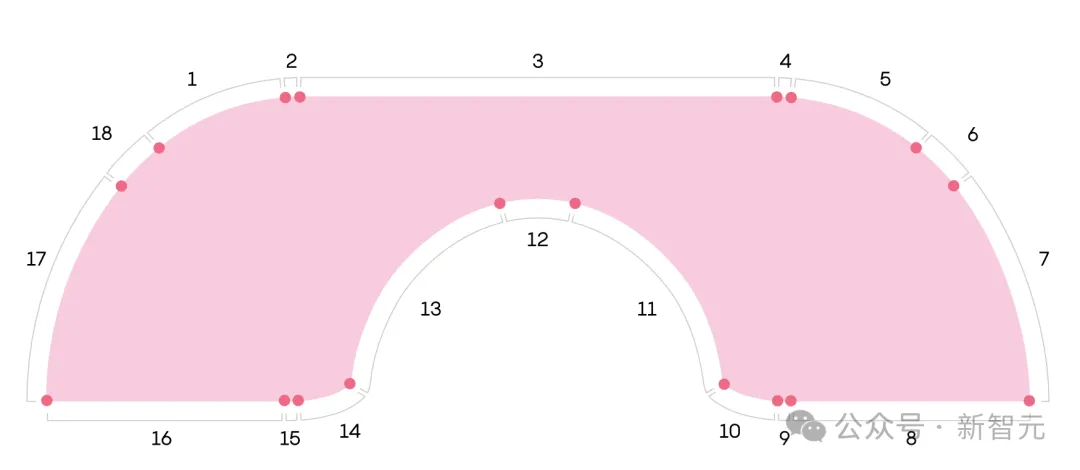
作者这样定义Gerver的沙发G：刻度标记表示构成G边界的18条解析曲线和线段的端点。右侧显示了包含G的支撑走廊Lt，以灰色表示。
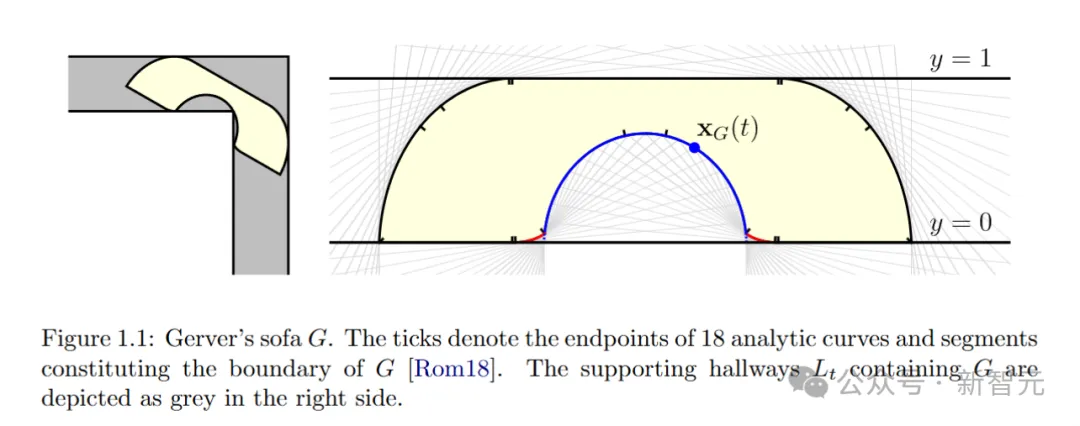
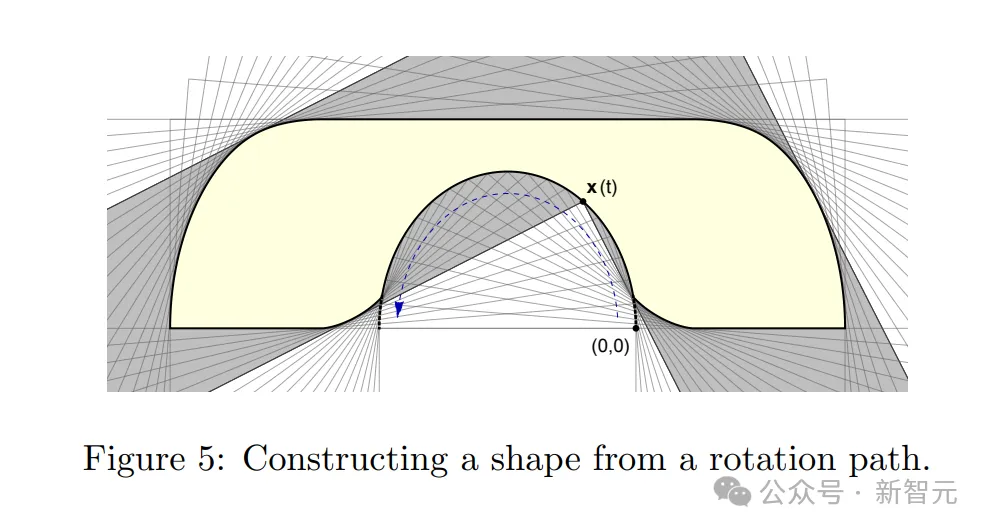
Gerver的一个基本思想，就是将移动沙发S看作是旋转走廊的交集。
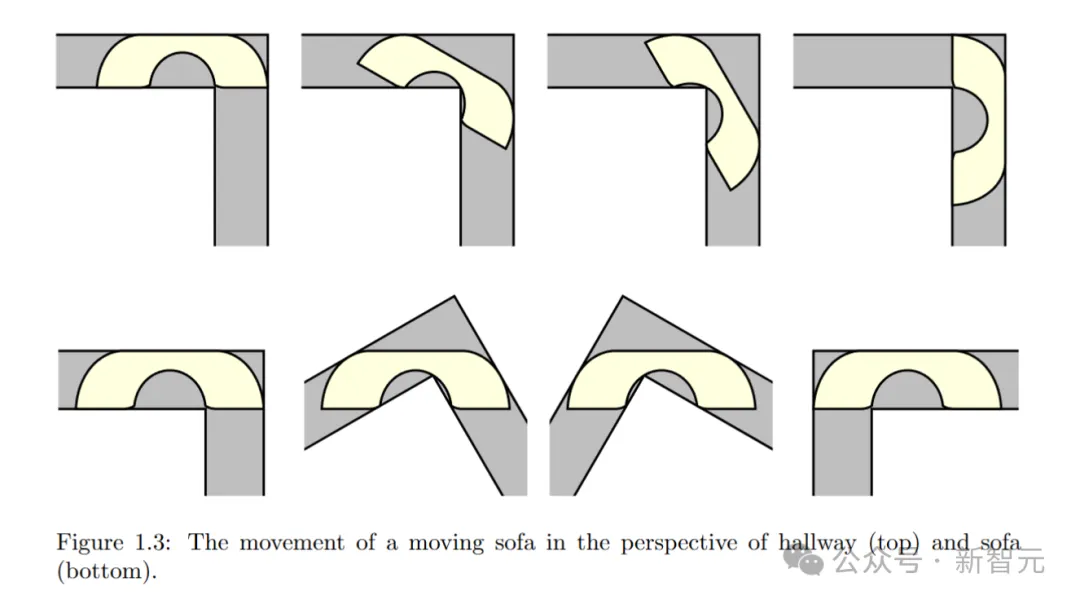从S的视角来看，S在走廊L内的运动。此时S在参考框架中是固定的，而L则围绕S旋转和平移，同时始终包含S。因此，S是旋转走廊的一个共同子集
在这篇论文中，作者证明了以下定理。
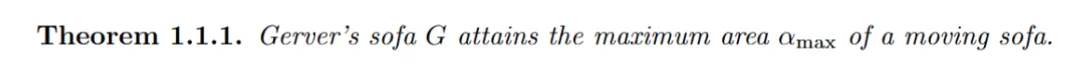
这个问题之所以困难，是因为没有一个通用的公式可以计算所有可能的移动沙发的面积。
为了解决这一问题，研究者证明了一个称为单射性条件的性质，该条件适用于最大面积的移动沙发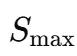
。
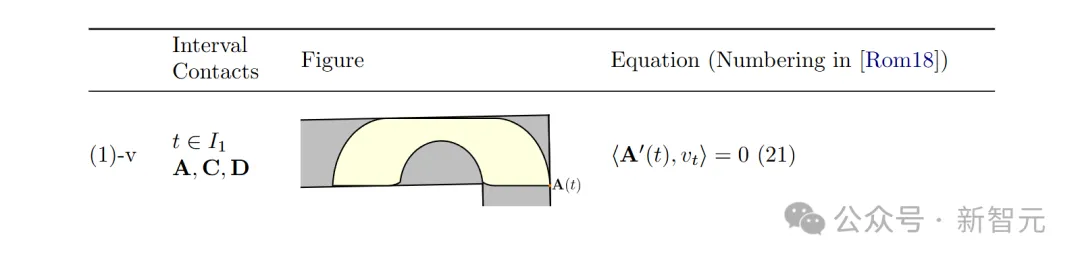
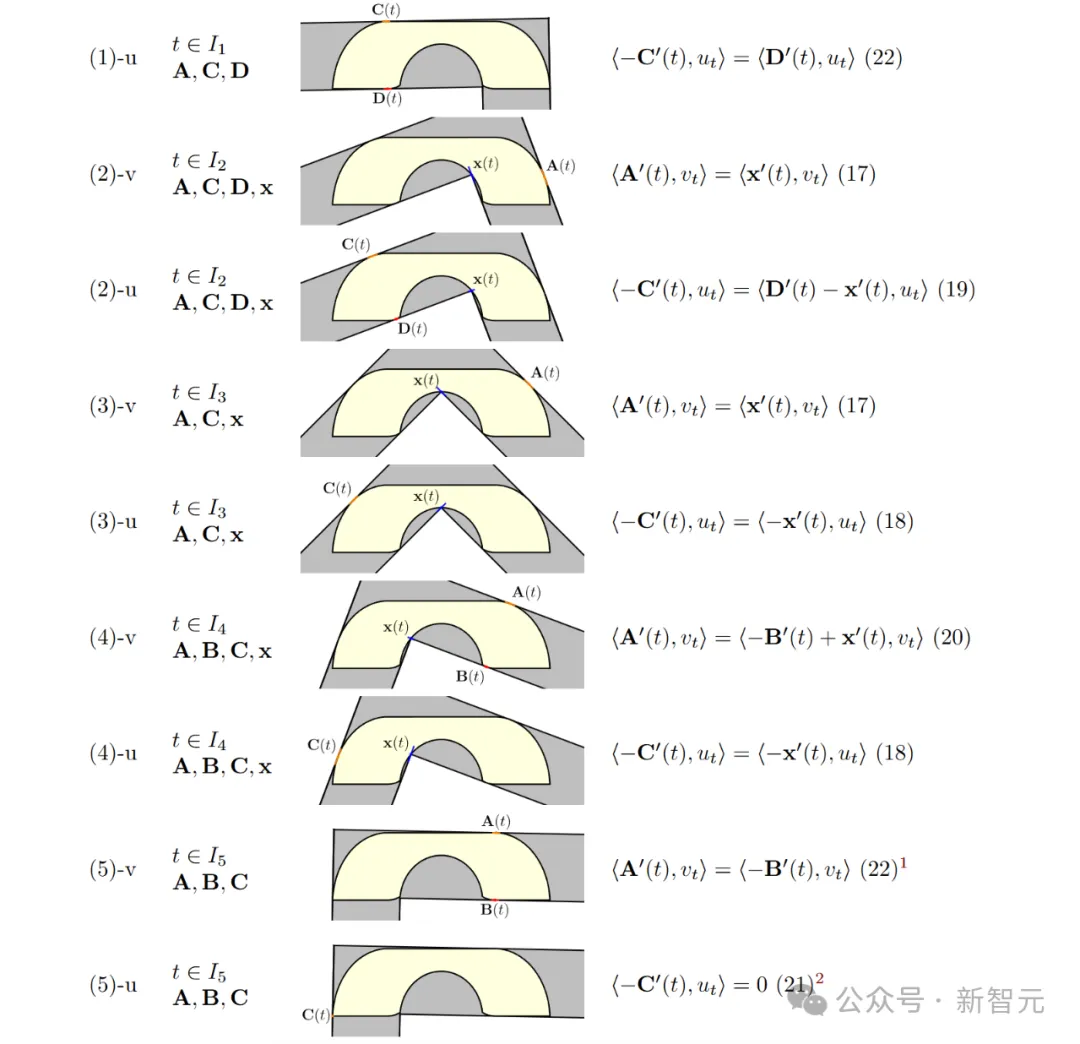
对于满足该条件的每个移动沙发S，都将定义一个更大的形状R，其形状类似于Gerver的沙发（见图1.2）。
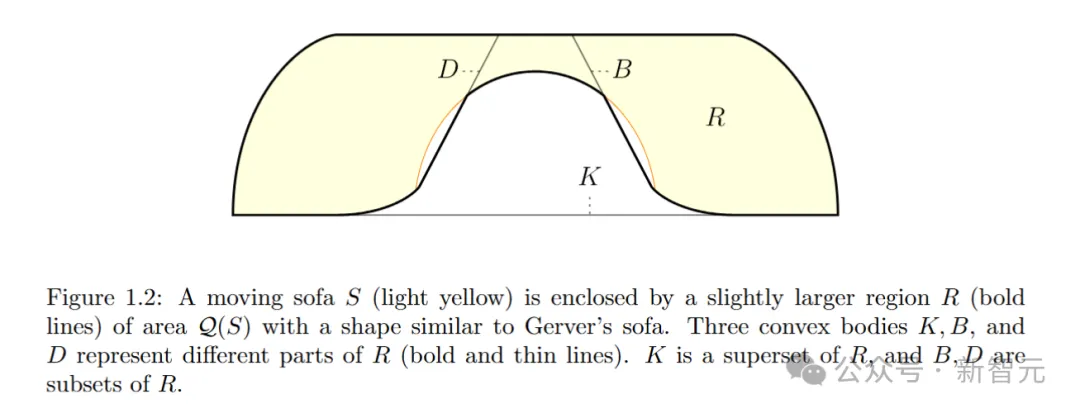
然后，R的面积Q(S)作为S面积的上界，并且当S是Gerver的沙发G时，Q(S) 恰好等于S的实际面积。
S的单射性条件确保区域R的边界形成一个Jordan曲线，使我们能够利用格林定理计算Q(S)。
为此，需要证明以下三点：
1. 缩小最大面积移动沙发S_max的可能形状范围。
2. 证明S_max满足单射性的条件。
3. 在单射性条件下建立沙发面积的上界Q。
接下来将S_max的形状缩小为单调沙发，以下就是单调沙发S在走廊视角（左）和沙发视角（右）下，以旋转角ω=π/2运动的情况。
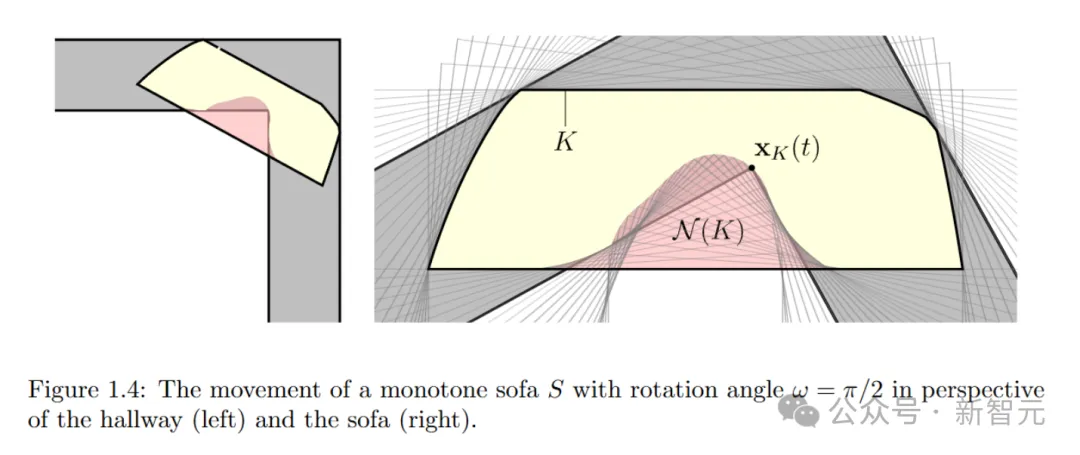
然后，研究者证明了S_max的边长应该互相平衡。
他们重新推导了Gerver关于定理1.3.1的证明，证明了平衡最大沙发的存在，即存在一种具有最大面积的单调沙发，它可以被平衡多边形以足够接近的程度逼近。
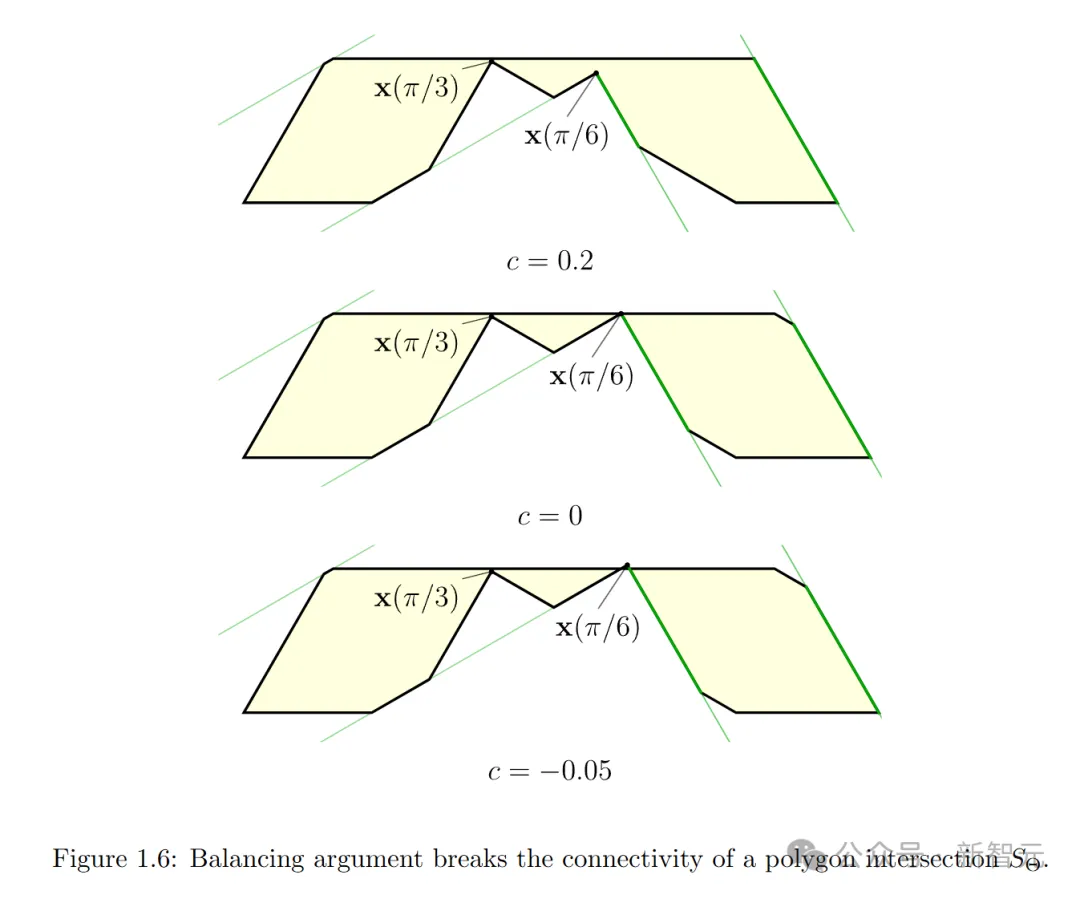
随后，他们证明了在前一阶段找到的平衡最大沙发允许以旋转角π/2进行运动。
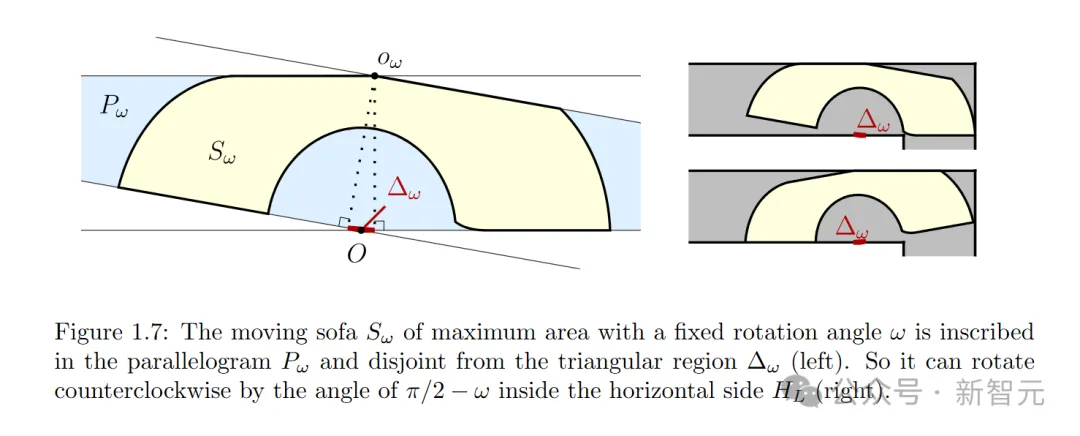
在论文最后，研究者提取了Gerver沙发G的相关性质，证明了G是全局最优解。
