LLaMA是目前很多SOTA开源大模型的基础,包括DeepSeek、千问等在内的很多大模型的模型机构大体上都沿用了LLaMA。因此,LLaMA在模型结构的设计上可以说是目前大模型的一种最佳实践。这篇文章就给大家汇总一下LLaMA的核心模型结构。
LLaMA的主体结构仍然基于Transformer,本文主要介绍LLaMA各个版本相比于Transformer的改进部分,包括Pre-Normalization、RMSNorm、SwiGLU激活函数、Rotray Embedding等部分。
1.Pre-Normalization
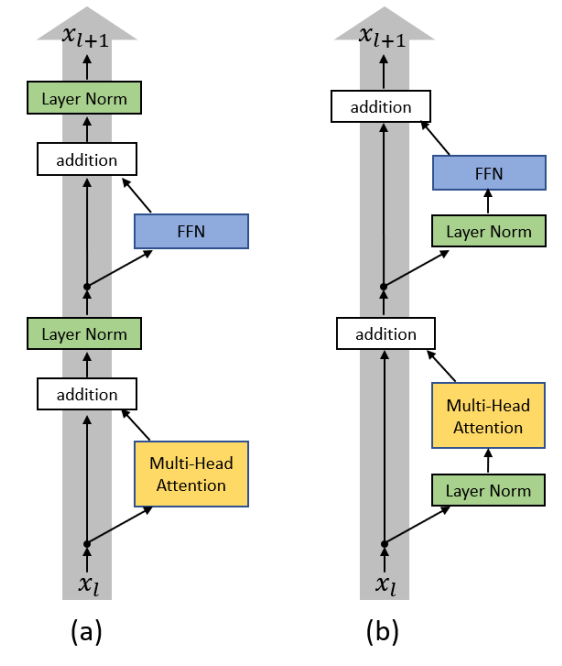
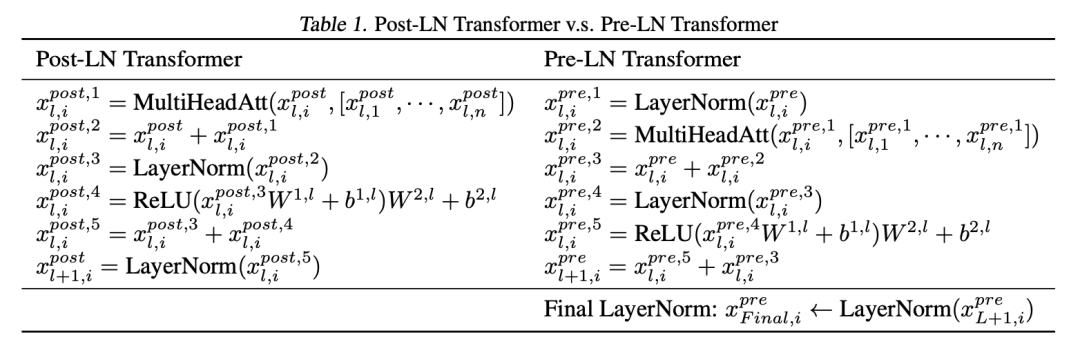
基础的Transformer每一层的计算逻辑是attention->add->norm->ffn->add->norm。其中norm为LayerNormalization。这种在attention和add之后的norm称为Post-Normalization。而LLaMA中采用了Pre-Normalization,主要源自于ON LAYER NORMALIZATION IN THE TRANSFORMER ARCHITECTURE(ICLR 2020)这篇文章。其核心是将LayerNormalization放在每层Transformer的输入位置。两者的差异如下图和表所示。
 图片
图片
 图片
图片
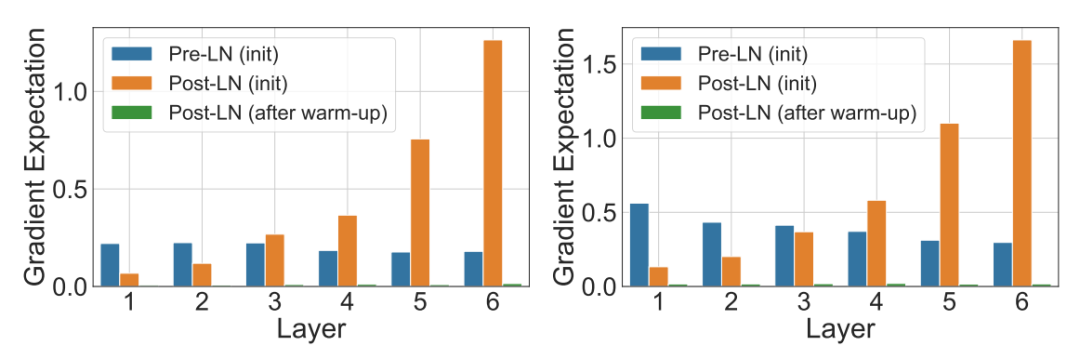
文中通过分析实验和分析发现,Post-Normalization方法在训练开始阶段模型的输出层的梯度范数比较大,模型层数越靠后梯度越大,这给训练的初始阶段带来了不稳定性。而使用Pre-Normalization,各层的梯度范数基本想同,因次使用Pre-Normalization可以提升训练的稳定性。此外,通过warm-up等策略,让初始的学习率小一些,可以缓解Post-Normalization的这种初始阶段梯度范数较大的问题。
 图片
图片
2.RMSNorm
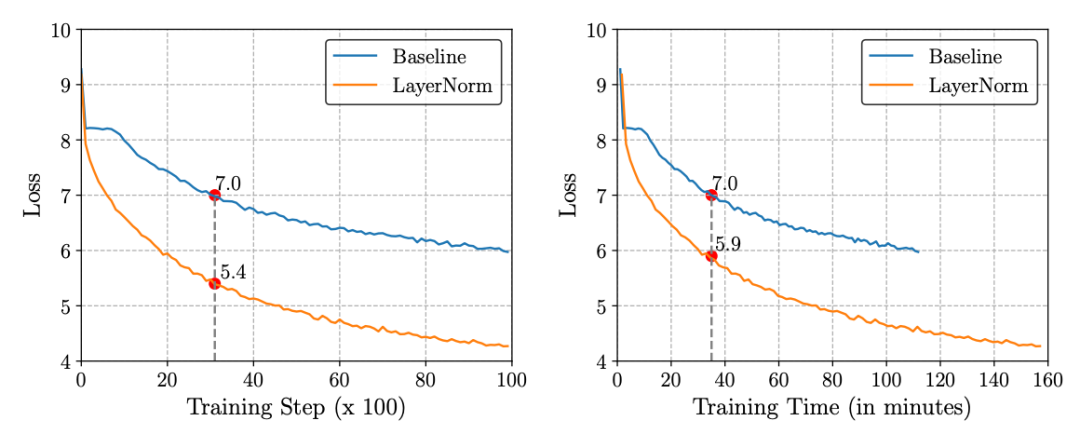
基础的Transformer在norm部分采用的是LayerNormalization,在LLaMA中则使用了RMSNorm,是一种针对LayerNormalization的改进,出自论文Root Mean Square Layer Normalization(NeuIPS 2019)中。LayerNorm每一层需要计算输入的每条样本向量各个元素的均值和方差,然后对输入进行归一化处理。这种方法虽然可以提升训练稳定性,但是大幅增加了模型中的计算开销。如下图,相同步数下使用LayerNorm可以降低1.6的loss,而相同时间下只能降低1.1的loss,说明LayerNorm的计算开销较大。
 图片
图片
为了解决这个问题,文中提出的RMSNorm将LayerNorm进行了简化,原来的LayerNorm是计算均值和方差,而RMSNorm改为计算元素的均方根,用均方根进行归一化。这样做虽然牺牲了LayerNorm对输入数据的re-centering能力,但是最终效果和LayerNorm差不多,说明LayerNorm的有效并不来源于re-centering。
 图片
图片
从实验效果看,使用RMSNorm模型收敛更快,也取得了更好的效果。
 图片
图片
3.SwiGLU
基础的Transformer结构中,激活函数使用的是ReLU。而LLaMA中将所有ReLU更换为SwiGLU激活函数,以此来提升模型的表现。SwiGLU发表于文章GLU Variants Improve Transformer(2020)中,SwiGLU是Swish激活函数和GLU激活函数的结合,Swish、GLU、SwiGLU激活函数的形式分别如下:
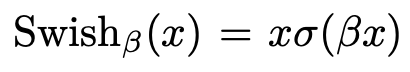 图片
图片
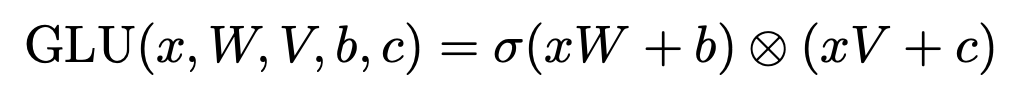 图片
图片
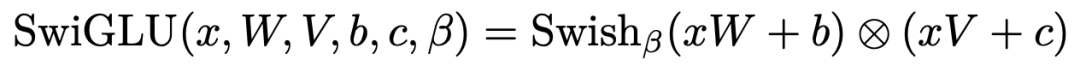 图片
图片
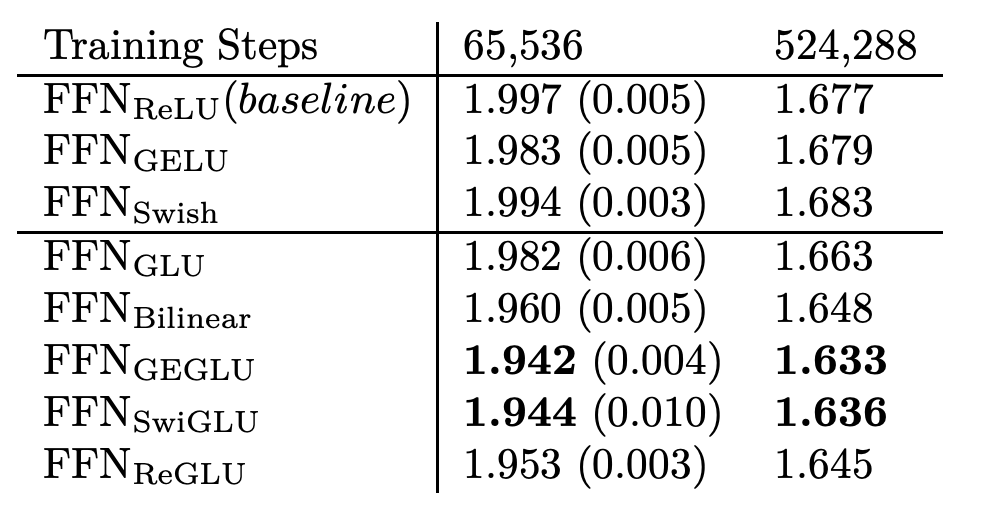
这里面的核心是利用了门控的思路,原始的输入过一个sigmoid,得到一个0~1的和输入向量维度相同的gate,以此对原始输入各个维度进行缩放。论文中在基于Transformer Encoder-Decoder的语言模型中,分别进行了预训练、finetune等不同激活函数的效果测试,都验证了SwiGLU相比ReLU等其他激活函数可以取得更好的效果。
 图片
图片
4.Rotary Position Embedding
基础的Transformer中采用绝对位置编码,即每个位置映射成一个embedding,或者用三角函数定义位置编码。但是绝对位置编码的核心问题在于,无法支持超出训练长度的建模,因为这些embedding在训练过程中没见过。在文本生成中,需要灵活支持很长的文本生成场景,因此绝对位置编码的弊端就显露出来。
旋转位置编码发表于论文ROFORMER: ENHANCED TRANSFORMER WITH ROTARY POSITION EMBEDDING(2023)中,是一种相对位置编码方法,能够灵活支持不同长度的文本输入和输出。其核心出发点是将位置编码信息放到attention的计算中,通过query和key的内积引入相对编码,目标是寻找一个函数f,其内积能够实现只和query和key的向量输入,以及两个元素的相对位置相关:
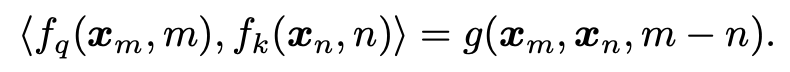 图片
图片
对应的函数在2维的情况下可以表示为如下形式,满足上述需求:
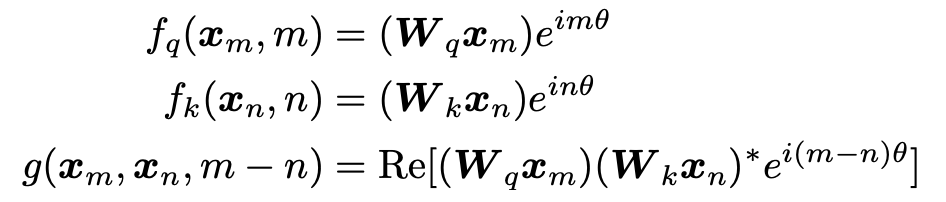 图片
图片
这里利用了复数的计算实现相对位置编码,整体的计算流程未,对于 token 序列中的每个词嵌入向量,首先计算其对应的 query 和 key 向量,然后对每个 token 位置都计算对应的旋转位置编码,接着对每个 token 位置的 query 和 key 向量的元素按照 两两一组应用旋转变换,最后再计算 query 和 key 之间的内积得到 self-attention 的计算结果。下图是论文中的示意图计算流程示意图。
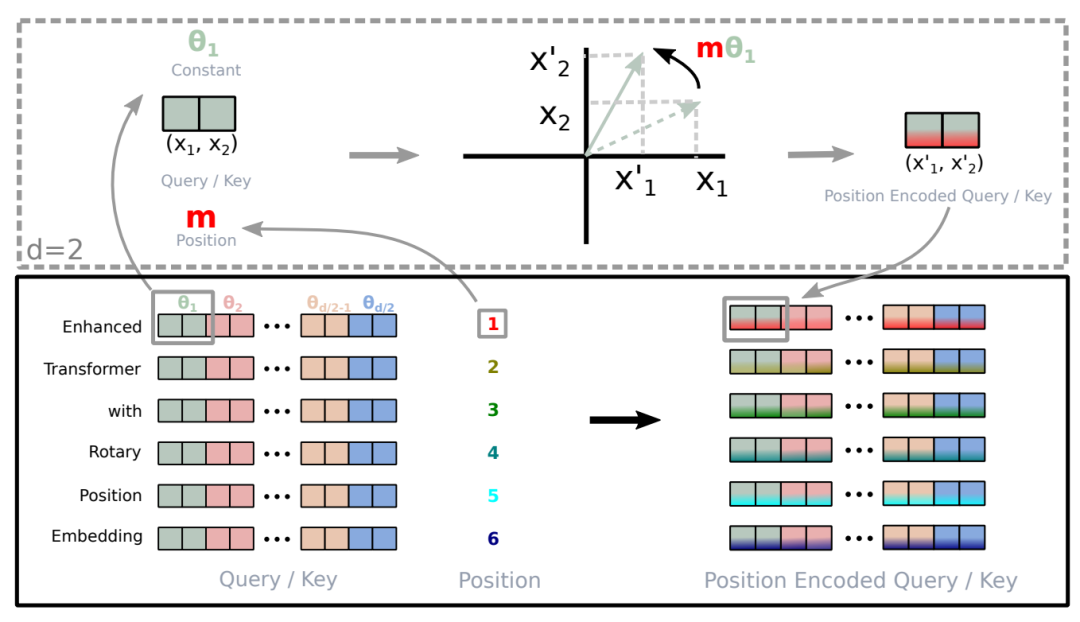 图片
图片
5.Grouped-Query Attention
为了提升infer的运算效率,LLaMA将基础Transformer中的self-attention改成了GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints(2023)中提出的grouped-query attention。在多头self-attention中,每和head内都会进行一次QKV的映射,再进行attention计算。而Grouped-query会将多个head分成多个组,每个组内的query使用相同的K和V,而不再每个head都进行一次映射,以此节省计算开销。
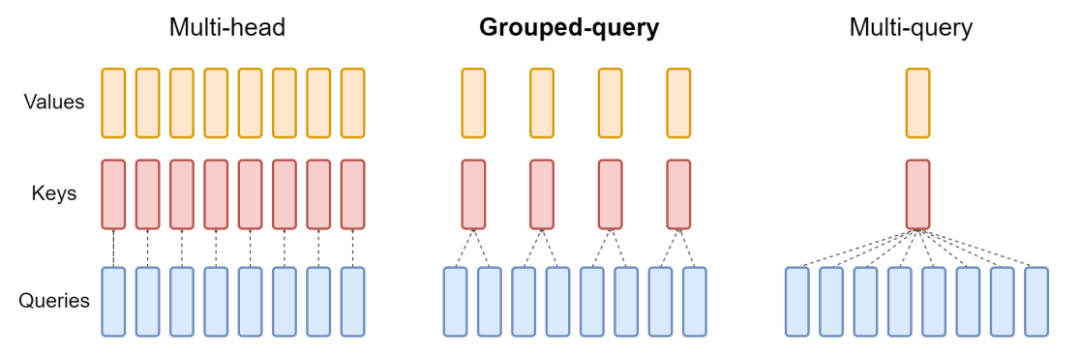 图片
图片








































