布隆过滤器(Bloom Filters)是一种不太为人所知的数据结构,目前开发者并没有广泛使用它。不过,布隆过滤器是一种高效节省空间且高度依赖概率的数据结构,每一位开发者都应当对其有所了解,它能够在很大程度上加快精确匹配查询的速度,尤其是在没有为该字段添加索引的情况下。布隆过滤器的空间效率还带来了额外的优势,即可以为多个字段创建过滤器。
布隆过滤器的工作原理
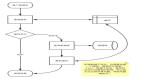
从数据库或存储中读取数据是一项成本较高的操作。为了优化这一过程,我们使用布隆过滤器来检查键值对是否存在,只有当过滤器返回“是”的时候,我们才会执行数据库读取操作。布隆过滤器节省空间,可以存储在内存中。此外,对一个值进行查找测试可以在O(1)时间内完成。稍后会详细介绍这一点。让我们通过一个例子来探讨这个概念:

我们为键“Key1”创建了一个布隆过滤器。当客户端请求与“Key1”的任何值相关联的数据时,我们首先通过布隆过滤器传递该值以检查其是否存在。在上面的图中,我们尝试读取与“Key1”的三个不同值相关联的有效载荷:
- 对于第一个值“Value1”,过滤器返回“否”,这使我们能够中断读取操作并返回“不可用”。
- 在第二个例子中,“Value2”存在于数据库中。过滤器返回“是”,这促使我们执行数据库读取以检索与“Key1”等于“Value2”相关联的有效载荷。
- 第三个例子更为有趣:过滤器对“Value3”返回“是”,但数据库中不存在与“Key1”等于“Value3”相关联的有效载荷。这被称为假阳性。在这种情况下,执行了数据库读取,但没有返回任何值。
尽管可能会出现假阳性,但永远不会出现假阴性——这意味着不可能存在一个键值对,而过滤器返回“否”。
如何实现布隆过滤器
布隆过滤器是一个长度为“n”的位数组,所有值都初始化为0。它需要“h”个不同的哈希函数来填充位数组。当一个值被添加到过滤器中时,每个哈希函数都应用于该值,以生成一个介于0和n之间的数字,并在位数组中设置相应的“h”个位。

为了测试一个元素是否存在于数组中,我们将相同的哈希函数集合应用于该元素,生成介于0和n之间的“h”个索引。然后,我们检查这些索引对应的位数组中的相应位是否被设置为1。如果所有位都被设置为1,则认为是命中,过滤器返回“真(true)”。

如上例所示,Value1、Value2和Value3被添加到过滤器中。每个值都通过三个哈希函数,并将位数组中对应的位设置好。之后,在测试阶段,Value1、Value4和Value5通过相同的哈希函数集来确定这些值是否存在。
由于哈希函数的特性和其有限的输出值范围,多个输入可能会生成相同的哈希值,从而导致冲突。冲突可能会导致假阳性,如Value5的情况所示。
选择合适的哈希函数和足够长度的位数组有助于减少冲突。此外,了解可能输入值的范围,例如所有有限范围内的字符串或数字,可以帮助选择最优的哈希函数和位数组长度。
时间和空间复杂度
哈希函数的运行时间为O(1),使得设置和测试操作均为常数时间操作。所需空间取决于位数组的长度,然而,与传统索引相比,布隆过滤器所占空间极小,因为它并不存储实际值,而只是为每个值存储几个比特。
限制条件
- 布隆过滤器仅支持精确匹配,因为其操作依赖于通过哈希函数传递输入,这需要精确匹配。
- 从布隆过滤器中删除一个值并非易事,因为数组中的位不能简单地被重置。数组中设置的位可能对应多个值。若要支持删除操作,则需要重新创建位数组。
- 如果哈希函数和位数组长度选择不当,可能会导致假阳性数量增加,使过滤器效率低下,甚至可能成为负担。在最坏的情况下,添加完所有值后,数组中的所有位都可能被设置。在这种情况下,任何测试都会从过滤器中得到肯定的响应。为解决此问题,可以使用调整大小的位数组和针对需求定制的新哈希函数重新创建过滤器。
写在最后的话
希望这篇文章能为你介绍布隆过滤器(如果你之前还不熟悉的话),并为你提供一个有价值的数据结构来扩展你的知识。和其他任何数据结构一样,它的使用取决于特定的用例,但在合适的机会出现时,它可能会非常有用。
原文标题:An Introduction to Bloom Filters,作者:Sandeep Kumar Gond