数学世界充满了无法触及的角落，那里存在着许许多多无法解决的问题。现在，又一个角落被照亮了。
1900 年，著名数学家大卫・希尔伯特（David Hilbert）公布了一份清单，其中包含 23 个关键问题，并希望以此指导下个世纪的数学研究。他的问题不仅为数学领域提供了路线图，还反映了一个更雄心勃勃的愿景 —— 建立一个坚实的基础，使得所有数学真理都可以基于此推理出来。
这个愿景很宏大，而其中的一大关键是假定数学是「完备的（complete）」。也就是说，所有数学陈述都应该可以被证明为真或假。
1930 年代，库尔特・哥德尔（Kurt Gödel）证明这是不可能的：在任何数学系统中，都有既不能证明也不能证伪的陈述。几年后，艾伦・图灵（Alan Turing）等人基于他的工作，表明数学充斥着「不可判定（undecidable）」的陈述 —— 即任何计算机算法都无法解决的问题。
这些结果表明，证明和计算的能力存在一些根本性限制。有些数学根本无法被人知晓。
希尔伯特的梦想破灭了。但它的碎片依旧继续存在着。他曾提出的那些问题仍会让人想起他的愿景，使「完备数学」的理念可在更狭窄的语境下生存。
在这些问题中，第十问题是最主要的一个，其与丢番图方程（又称不定方程）有关。丢番图方程是指有整数系数的多项式，例如 x² + y² = 5。我们很熟悉这些方程，而它们也是数学领域最核心的研究对象之一。几千年来，数学家一直在寻找它们的整数解。例如，在这个例子中，一个解是 x = 1，y = 2（因为 1² + 2² = 5）。另一个是 x = 2，y = −1。
大卫・希尔伯特
x² + y² = 3 等许多丢番图方程却可能没有任何整数解。希尔伯特的第十问题是：是否总是可以判断给定的丢番图方程是否有整数解。是否存在一种算法可以确定每个方程的解，还是说这个问题是不可判定的？也许不可能为所有数学问题找到一种完备而系统的求解方法 —— 甚至不可能解决希尔伯特的所有 23 个问题 —— 但对于丢番图方程，可能仍然存在一种求解方法，作为希尔伯特理想的一个微缩版本。乌得勒支大学的 Peter Koymans 说：「这个问题是那个梦想的一个非常自然的版本。」
1970 年，一位名叫 Yuri Matiyasevich 的俄罗斯数学家打破了这个梦想。他的研究表明，并不存在一种可以确定任何给定的丢番图方程是否有整数解的通用算法 —— 希尔伯特第十问题是一个不可判定的问题。你也许能够构想出一种可以评估大多数方程的算法，但它无法适用于每一个方程。
即使在这种最简单的数学中，也隐藏着不可知性。
Yuri Matiyasevich，摄于 1969 年
数学家们想检验 Matiyasevich 的结论的适用范围。比如如果允许丢番图方程有复数解（可以用实部和虚部写出的数字，并且不限于整数）呢？在这种情况下，每个丢番图方程都有一个解，而希尔伯特第十问题的答案是肯定的。但是，在解必须是整数的方程和解可以是复数的方程之间，丢番图方程还存在很广的范围。
「对于整数，它是不可求解的，然后当传递给更大的数字系统时，可能会突然获得可解性。」哈佛大学的 Barry Mazur 说。「但这个转折点在哪里？」
自希尔伯特第十问题被解决以来的 50 年里，数学家们一直在寻找这个转折点。现在，Koymans 和他的长期合作伙伴、蒙特利尔康考迪亚大学的 Carlo Pagano 以及另一组独立研究的团队朝着这一目标迈出了重要一步。
这两个小组都证明，对于整数之外的大量重要数集，同样不存在可确定任意给定的丢番图方程是否有解的通用算法。这两项工作不仅让数学家能够更精确地了解他们能知道什么和不能知道什么，还让他们对数学中最核心的对象之一有了全新的控制水平。
- 论文标题：Hilbert's tenth problem via additive combinatorics
- 论文地址：https://arxiv.org/abs/2412.01768
- 论文标题：Rank stability in quadratic extensions and Hilbert's tenth problem for the ring of integers of a number field
- 论文地址：https://arxiv.org/abs/2501.18774
从整数开始扩展
这些新证明的核心是希尔伯特第十问题的一种自然扩展。该扩展涉及的丢番图方程的解属于一个与整数密切相关的数字系统。
从 1 和 -1 开始，可以通过不同的组合方式得到所有其它整数。但如果是从 1、-1、和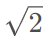 
开始呢？通过不同组合方式，也能得到一个数字系统，这被称为整数环（ring of integers）。很显然，名字虽然是整数环，但这个数字系统中并不只有整数。使用其它的数字集合也能构建其它的整数环，比如可包括 
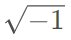（也就是虚数 i）或 
。
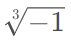那么，问题来了：是否存在一种算法，可以总是确定给定丢番图方程的解是否属于某个整数环？
Carlo Pagano
数学家猜想，对于每一个整数环（即无限多个数字系统），这个问题仍然是不可判定的。这将使该结论远远超出希尔伯特第十问题初始的整数范围。
为了证明这一点，他们希望追随原始问题的证明脚步 —— 仅涉及整数解的问题。
一般来说，不可判定性证明（确定是否存在可以回答给定问题的通用算法的证明）遵循相同的方法：证明相关问题等价于计算机科学中一个著名的不可判定问题，即停机问题（halting problem）。停机问题问的是：对于一个理想的计算设备（称为图灵机），当给定某个输入时，该设备将永远运行还是最终会停止？现在人们已经知道，并不存在一个可为每台图灵机解答这个问题的算法。
也可以将丢番图方程视为计算设备。以方程 y = x² 为例。它有无穷多个整数解。只需为 x 代入不同的整数并求解 y，得到的值都属于一个著名的整数集：完全平方数（the perfect squares）。我们很容易就能想象出一个能执行其等价任务的计算机程序（即图灵机）：「计算完全平方数的序列」。
其它丢番图方程也可以编码成其它类型的计算。
Julia Robinson
为了解决希尔伯特最初的第十问题，数学家们以这个想法为基础开始了研究。Julia Robinson 等人于 1950 年左右开始研究，最终汇集成了 1970 年 Matiyasevich 的成果。研究结果表明，对于每个图灵机，都有一个对应的丢番图方程。「这完全出乎意料，」智利天主教大学的 Hector Pasten 说。「基于整数的丢番图方程足以定义你能想象到的任何东西。」
此外，数学家们还建立了一种优雅的对应关系：如果图灵机因给定输入而停止，其对应的丢番图方程将有一个整数解。如果图灵机永远运行，其对应的丢番图方程将没有解。但这意味着希尔伯特第十问题编码了停机问题：如果一种算法可以根据是否有整数解对丢番图方程进行分类，那么该算法也可用于根据是否会停机对图灵机进行分类。
换句话说，希尔伯特第十问题是不可判定的。
数学家们希望采用同样的方法来证明该问题扩展的整数环版本 —— 但他们遇到了一个障碍。
将研究成果黏合起来
当允许方程有非整数解时，图灵机和丢番图方程之间的有用对应关系就会瓦解。再次以方程 y = x² 为例。如果你研究的是包含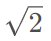 
的整数环，那么你最终会得到一些新的解，例如 x = 
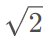, y = 2。该方程不再对应于计算完全平方数的图灵机 —— 更广义地说，丢番图方程不再能编码停机问题。
但在 1988 年，纽约大学的一名研究生 Sasha Shlapentokh 开始想办法解决这个问题。到 2000 年，她和其他一些研究者制定了一个计划。假设你要为 y = x² 添加一些其它项，从而可迫使 x 再次为整数，即便要使用不同的数字系统。然后，你可以挽救与图灵机的对应关系了。那所有丢番图方程都可以这样做吗？如果可以，那就意味着希尔伯特问题可以在新的数字系统中编码停机问题。
多年来，Shlapentokh 等数学家弄清楚了他们必须在各种环的丢番图方程中添加哪些项，这使他们能够证明希尔伯特问题在这些设置下仍然无法判定。然后，他们将所有剩余的整数环归结为一种情况：涉及虚数 i 的环。数学家们意识到，在这种情况下，必须添加的项可以使用一类名为椭圆曲线（elliptic curve）的特殊方程来确定。
但椭圆曲线必须满足两个属性。首先，它需要有无限多个解。其次，如果切换到不同的整数环 —— 如果从数字系统中移除虚数 —— 那么该椭圆曲线的所有解都必须保持相同的底层结构。
事实证明，构建这样一条适用于所有剩余环的椭圆曲线是一项极其微妙和困难的任务。但 Koymans 和 Pagano—— 从研究生阶段就开始就密切合作的椭圆曲线专家 —— 拥有合适的工具集来进行尝试。
许多个不眠之夜
从本科开始，Koymans 就一直在思考希尔伯特第十问题。在就读研究生以及在与 Pagano 合作期间，这个问题一直在召唤他。「我每年都会花几天时间思考这个问题，但总是陷入困境，」Koymans 说。「我尝试了三种方法，但它们都失败了。」
2022 年，在加拿大班夫举行的一次会议上，他和 Pagano 最终聊到了这个问题。他们希望能够一起构建出解决这个问题所需的特殊椭圆曲线。在完成了其它一些项目后，他们开始了研究。
Peter Koymans
他们从一个简单的椭圆曲线方程开始，这个方程不满足任何所需的属性。他们知道他们可以使用一种名为二次扭曲（quadratic twist，这是他们已经研究了近十年的东西）的成熟技术来调整方程，使其满足第一个条件。他们只需将方程的一个变量乘以一个特定的数字，他们就会得到一条有无限多个解的新椭圆曲线。
但这给他们留下了一个问题。他们无法保证这条新曲线满足第二个性质 —— 对于相差一个虚数的环，其解看起来会很相似。数学家们需要更好地控制二次扭曲。
他们陷入困境。「我有一种不好的感觉，」Koymans 说。「我开始怀疑我们遗漏了什么东西。」
然后，在 2024 年夏天，在研究另一个问题时，两人不得不再次使用二次扭曲。一天晚上，在这项研究过程中，科伊曼斯发现自己躺在床上睡不着，无法停止思考希尔伯特第十问题。
Koymans 意识到，另一项工作给了他们一个重要的提示，即那些有时会出现的奇怪且惊人的数学一致性（mathematical concordance）：如果他们在二次扭曲中使用的数字恰好是三个素数的乘积，则他们就会获得保证第二个性质所需的控制权。但是，由于他们的椭圆曲线必须精心构建并满足许多规范，因此对这三个素数的取值有很多额外的限制。Koymans 和 Pagano 能找到可行的素数吗 —— 不管对于哪个整数环？
几天后，Pagano 碰巧计划访问当时 Koymans 工作的瑞士苏黎世联邦理工学院。接下来的一周，他们一起在黑板上努力寻找满足所有限制的素数。最后，他们发现必须使用四个素数而不是三个素数来构建所需的二次扭曲。这使得他们能够应用一种来自完全不同的数学领域的方法，即加性组合学（additive combinatorics），以确保每个环都存在正确的素数组合。
这就是最后一部分：他们构建了所需的椭圆曲线。它为他们提供了向丢番图方程添加项所需的方法，这使他们能够将图灵机（以及停机问题）编码到这些方程中，而不管他们使用什么数字系统。一切都解决了。希尔伯特第十问题对于每个整数环都是不可判定的。
上周四，在 Koymans 和 Pagano 在线发布他们的论文不到两个月后，结果得到了进一步巩固。一个由四名数学家组成的独立团队宣布了对同一结果的新证明。他们没有寻找特殊的椭圆曲线，而是依靠一种不同类型的方程来完成同样的工作。
这两个团队都希望利用他们的技术（这些技术使他们对椭圆曲线和相关方程有了前所未有的控制）在其他问题上取得进展。普林斯顿大学数学家、第二个证明的作者之一 Manjul Bhargava 说：「这两种方法有可能结合起来做更多的事情。」
与此同时，对不可判定性终结以及可判定性开始的位置的探索尚未结束：数学家们正在新的环境中继续探索希尔伯特第十问题。
蒙特利尔大学的 Andrew Granville 认为，这只是众多问题中的一个，这些问题「反映了世界哪些部分为真的哲学方面」。
所有知识都有极限。Granville 说：「它提醒我们，有些事情是无法做到的 —— 无论你是谁，无论你有怎样的身份或才智。」
