在数据分析与建模中，许多插值和模拟方法要求输入数据服从正态分布。而正态分数变换（Normal Score Transformation，NST）正是一种将数据转化为标准正态分布的有效方法。通过该方法，我们可以将原始数据集转化为一个与标准正态分布相似的数据集，从而满足某些分析方法的需求。正态得分变换的核心步骤包括：首先对数据集进行排序并赋予秩次，然后根据秩值在标准正态分布中找到对应的分位数，最后通过这些正态分布的值构成变换后的数据集。在实际应用中，秩次的计算可以通过频率分布或累计分布来完成，确保变换结果准确、可靠。
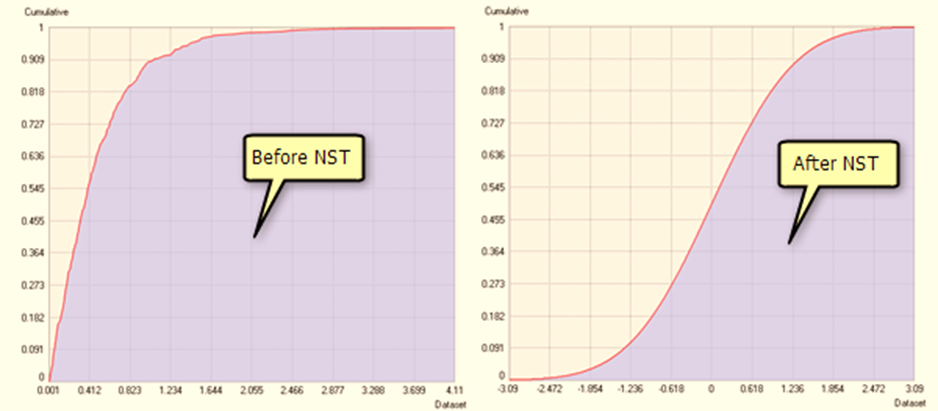
下面展示了应用正态得分变换前后，直方图和累积分布的示例：
图片
图片
如何进行正态分数变换 (Normal Score Transformation）
对非正态分布的数据进行正态分数转换（normal score transformation），也称为秩正态化（rank normalizing）。具体步骤如下：
生成秩向量：首先，对原始数据 x=(x1,x2,…,xn) 进行排序，得到一个秩向量 Rx=(Rx1,Rx2,…,Rxn)，其中 Rxi 表示数据点 xi 在所有观测值中的秩次。
转换为标准正态分布：接下来，使用秩值来计算正态分数。对于每个 xi，将秩值 Rxi 转换为正态分布的分位数，计算公式为：
图片
其中，ϕ−1 是标准正态分布的逆累积分布函数（即将概率值转换为正态分布下的对应值）。
这种方法的核心是通过秩排序将非正态数据映射到正态分布空间中，从而使数据更符合正态分布，通常用于统计分析或机器学习模型的前处理。
下面的python 代码实现：
import numpy as np
from scipy.stats import rankdata, norm
# 假设有一组非正态分布的数据
x = [0.1, 0.2, 1.1, 1.5, 3.8, 5.4, 6.9, 6.6, 0.2, 0.2]
# 1. 计算秩向量
ranks = rankdata(x,method='average') # method {'average', 'min', 'max', 'dense', 'ordinal'}
# 2. 将秩向量转换为正态分数
n = len(x)
x_prime = [norm.ppf(rank / (n+1)) for rank in ranks]
print("原始数据:", x)
print("秩向量:", list(ranks))
print("正态分数:",[round(num,3) for num in x_prime] )
图片
- rankdata(x)：计算并返回数据的秩向量。秩是从 1 到 n 的整数，每个数据项对应它在排序中的位置。
- norm.ppf()：计算标准正态分布的逆累积分布函数（即将概率值映射到正态分布的分位数），这里的概率是通过 Rxi /(n+1) 计算得到的。
其他修正的方式
Blom’s formula：
图片
Blom’s 方法引入了一个修正项，使得尾部的正态分数更加接近实际分布。
Tukey’s formula：
图片
Tukey 的公式类似于 Blom，但调整项略有不同。
Van der Waerden's formula
图片
import numpy as np
from scipy.stats import rankdata, norm
# 原始数据
x = [0.1, 0.2, 1.1, 1.5, 3.8, 5.4, 6.9, 6.6, 0.2, 0.2]
# 方法 1: 使用 average 秩和 Van der Waerden's formula
ranks_average = rankdata(x, method='average')
n = len(x)
x_prime_vdw = [norm.ppf((rank - 0.5) / n) for rank in ranks_average]
# 方法 2: Blom's formula
x_prime_blom = [norm.ppf((rank - 3/8) / (n + 1/4)) for rank in ranks_average]
# 方法 3: Tukey's formula
x_prime_tukey = [norm.ppf((rank - 1/3) / (n + 1/3)) for rank in ranks_average]
# 打印结果
print("原始数据:", x)
print("平均秩:", list(ranks_average))
print("Van der Waerden:", [round(num,3) for num in x_prime_vdw])
print("Blom:", [round(num,3) for num in x_prime_blom])
print("Tukey:", [round(num,3) for num in x_prime_tukey])
图片
正态分数变换与 Z-Score 标准化变换的区别
正态分数变换（NST）和 Z-Score 标准化都是数据预处理中常用的方法，但它们的目标和实现方式有显著不同。
NST是一种非线性变换，通过将数据的秩次映射到标准正态分布的分位数，强制将非正态数据转换为严格的正态分布，适用于需要数据服从正态假设的场景（如克里金插值）；其优势在于对异常值不敏感且能重塑分布形态。而Z-Score是线性变换（基于均值和标准差），仅调整数据的中心位置和尺度，不改变原始分布形状，适用于消除量纲差异（如机器学习特征标准化），但对异常值敏感。两者分别服务于“分布形态修正”和“数值标准化”的不同需求。
以下是两者的主要区别：
图片
根据具体需求选择合适的方法：如果需要数据严格服从正态分布，使用正态分数变换；如果仅需消除量纲差异，使用 Z-Score 标准化。
正态分数变换（NST）是一种将非正态分布数据转化为接近标准正态分布的方法，主要通过对数据进行排序并根据秩值转换为正态分布分位数。与 Z-Score 标准化不同，NST的目标是使数据符合正态分布，而 Z-Score 标准化则主要用于消除量纲差异。NST常用于统计分析和机器学习模型的前处理，以确保数据符合正态性要求。
