译者 | 汪昊
审校 | 重楼
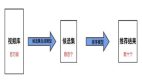
推荐系统在互联网行业应用广泛。根据亚马逊和Netflix 等公司的经验,推荐系统可以给公司带来大幅度的流量提升,从而起到开源节流的作用。试想如果不借助于推荐系统,而是借助于搜索引擎关键词进行引流,那么营销的花费将增加数倍乃至数百倍都有可能。因此,大型互联网公司对于推荐系统不管怎么重视都不为过。

业界对于推荐系统的研究,主要集中在如何提升推荐系统的准确率方面。随着近年来大模型的火热,在信息检索顶会上,曾经出现研究大模型 Scaling Law 的文章获得最佳论文奖的情况。而推荐系统领域在 2023 年也出现了一篇类似的文章,讲的是推荐系统矩阵分解模型中特征向量的维度的大小对于准确率的影响。这篇论文题目是 Curse of Low Dimensionality in Recommender System,发表在信息检索领域顶会SIGIR 2023 上。下面我们来一探这篇论文的究竟。
作者首先给出了推荐系统点乘模型的一般公式:
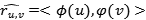
其中
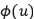
是用户侧的嵌入式向量,而
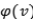
是物品侧的嵌入式向量。推荐系统点乘模型的一个典型例子是 Alternating Least Squares (ALS)。这个算法被集成在了 Apache Spark 的 MLLib 算法库里。作者在本文中将在 MovieLens 20M,Million Song Dataset 和 Epinions 数据集上测试 ALS 算法,以考察嵌入式向量的维度对于推荐系统准确率的影响。
作者通过对比实验检验流行度偏差,得到了下图:
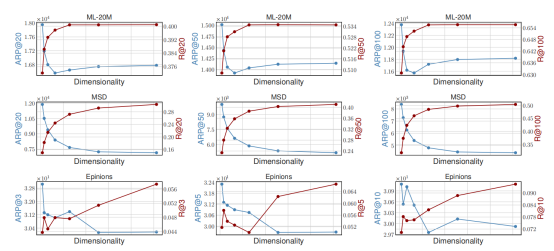
随后,作者检验了算法的召回率,得到了下图:
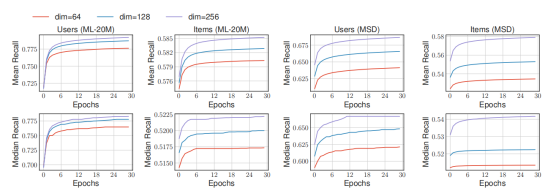
作者通过实验观察得到结论,高维度的嵌入式表达可以得到更高的准确度和更低的流行度偏差。
作者随后对于嵌入式表达进行了理论建模,得到了以下定理:
定理 4.1 以下结论成立:
- 上界:对于每一组在空间的 n 个物品向量来说,能利用这些向量表示的长度为 K 的排序列表数量至多数 。
- 下界: 存在一组在空间的物品向量,这组向量的数量是 n,能利用这组向量来表示的长度为 d 的排序列表数 。
以上定理表明增加嵌入式向量维度,会指数级别的增强点乘模型的表达能力。
为了研究流行度偏差背后的机理,作者随后又提出了如下定理:
定理 4.2 假定存在两个物品集合 P 和 L,查询向量 q 在点乘模型中总是将 P 集合中的物品排名优于所有的L 集合中的物品。那么,如果一个向量 s 被包括在一个凸锥中,而这个凸锥又包含了 P 的凸包,那么 s 比 L 中的每一个物品排名都高。另外,这个凸锥会随着更多物品的加入而变得更大。
这个定理告诉我们因为存在一小撮流形和长尾的物品,它们使得比较流形的物品排名优于长尾物品,降低了可表达的排序列表的数量,因此我们无法完全避免流行度偏差。
在本文中,作者根据实验和后续的理论分析指出低维嵌入式向量会导致关于流行度偏差的过拟合,并会进一步加深流行度偏差的问题。这一现象,被称为低维度诅咒。作者的研究工作条理分明,除了大量的实验对比工作,还进行了严谨的理论分析,因此值得推荐系统行业的从业者认真学习。
译者简介
汪昊,前达评奇智董事长兼创始人。前 FunPlus 人工智能实验室负责人。在 ThoughtWorks, 百度,联想,网易和 FunPlus 等科技公司有超过 13 年的技术和技术管理经验。精通推荐系统、金融风控、爬虫和聊天机器人等领域。在国际学术会议和期刊发表论文 44 篇。5 次获得国际学术会议最佳论文奖和最佳论文报告奖。2006 年 ACM/ICPC 北美落基山区域赛金牌。2004 年全国大学生英语能力竞赛口语总决赛铜牌。本科(2008年)和硕士(2010年)毕业于美国犹他大学。对外经贸大学(2016 年)在职 MBA 学位。