金融波动率的多模型建模研究：GARCH族与HAR模型的Python实现与对比分析-51CTO.COM

金融资产波动率建模在现代金融工程中具有重要地位，其应用涵盖风险管理、衍生品定价和投资组合优化等核心领域。本文着重探讨三种主流波动率建模方法：广义自回归条件异方差模型(GARCH)、Glosten-Jagannathan-Runkle-GARCH模型(GJR-GARCH)以及异质自回归模型(HAR)。本文将系统阐述这些模型的理论基础，并基于标准普尔500指数ETF(SPY)的实际交易数据进行实证分析。

理论基础

1、 GARCH模型

GARCH(1,1)模型由Bollerslev于1986年提出，该模型有效捕捉了金融时间序列中的波动率聚类特征。模型的数学表达式为：

r_t = μ + εtεt = σt * z_tσ²t = ω + α * ε²(t-1) + β * σ²(t-1)

其中各参数定义如下：

r_t 表示t时刻的资产收益率
μ 表示条件均值
εt_ 表示随机扰动项
σt_ 表示条件波动率
z_t 表示服从标准正态分布的随机变量
ω, α, β 为待估计参数集

该模型的核心特征在于：当前条件方差依赖于前期的随机扰动项平方(α项)和前期条件方差(β项)。模型的波动率持续性由α + β之和度量，该值通常接近但严格小于1，以确保过程的平稳性。

2、GJR-GARCH模型

GJR-GARCH模型由Glosten、Jagannathan和Runkle于1993年提出，是对标准GARCH模型的重要扩展。该模型通过引入杠杆效应项，刻画了金融市场中负向冲击对波动率的非对称影响。模型表达式为：

σ²t = ω + α * ε²(t-1) + γ * I(t-1) * ε²(t-1) + β * σ²_(t-1)

其中：

I(t-1)_ 为示性函数，当ε_(t-1) < 0时取值为1，其他情况为0
γ 为杠杆效应系数，用于捕捉负向收益率冲击的额外影响

通过引入γ参数，模型能够有效区分正负向市场信息对波动率的差异化影响，这一特性使其在股票市场波动率建模中表现出较强的实证效果，因为市场下跌通常会引发比上涨更显著的波动率反应。

3、HAR模型

HAR（异质自回归）模型由Corsi于2009年提出，该模型采用创新性的方法，通过整合不同时间尺度的波动率信息直接对已实现波动率进行建模。模型的基本形式为：

RV_t+1 = β₀ + βd * RV_t + βw * RV_t^w + βm * RV_t^m + εt+1

其中各变量定义如下：

RV_t 代表日度已实现波动率
RV_t^w 代表周度已实现波动率的算术平均值
RV_t^m 代表月度已实现波动率的算术平均值
β 系数集合反映了不同时间尺度波动率的边际贡献

实证分析与代码实现

本节详细阐述三种波动率模型的Python实现过程：

数据预处理

def get_spy_data():
     """获取SPY指数近五年交易数据"""
     end_date = datetime.now()
     start_date = end_date - timedelta(days=5*365)
     spy = yf.download('SPY', start=start_date, end=end_date)
     return spy
 
 def calculate_returns(prices):
     """计算连续复利收益率"""
     return 100 * np.log(prices / prices.shift(1))

本文采用对数收益率进行建模，这种处理方式具有两个主要优势：对数收益率具有可加性；对数收益率的分布通常更接近正态分布，这有利于后续的统计推断。

GARCH模型估计

def fit_garch(returns):
     """估计GARCH(1,1)模型参数"""
     model = arch_model(returns, vol='Garch', p=1, q=1)
     results = model.fit(disp='off')
     return results

GARCH模型的参数估计采用arch计量经济学库实现，该库基于最大似然估计方法提供了高效的参数估计功能。在实证研究中，GARCH(1,1)规范通常能够充分捕捉金融时间序列的波动率动态特征。

GJR-GARCH模型估计

def fit_gjr_garch(returns):
     """估计GJR-GARCH(1,1)模型参数"""
     model = arch_model(returns, p=1, o=1, q=1, dist='studentst')
     results = model.fit(disp='off')
     return results

GJR-GARCH模型的实现引入了非对称项参数(o=1)，并采用学生t分布来更好地拟合金融收益率分布的尾部特征。模型自动包含了负向收益的示性函数处理机制。

HAR模型

def calculate_har_volatility(returns, lookback=22):
     """构建HAR模型并估计已实现波动率"""
     rv = returns**2  # 计算日度已实现方差
     
     # 构造不同时间尺度的HAR组件
     rv_d = pd.Series(rv)
     rv_w = rv.rolling(window=5).mean()  # 构造周度波动率分量
     rv_m = rv.rolling(window=22).mean()  # 构造月度波动率分量
     
     # 生成预测变量矩阵
     X = pd.DataFrame({
         'rv_d': rv_d.shift(1),
         'rv_w': rv_w.shift(1),
         'rv_m': rv_m.shift(1)
    })
     
     # 处理缺失值
     y = rv[lookback:]
     X = X[lookback:]
     
     # 应用OLS方法进行参数估计
     X = X.fillna(0)
     beta = np.linalg.pinv(X) @ y
     
     # 计算波动率预测值
     har_vol = np.sqrt(252 * (X @ beta))  # 转换为年化波动率
     
     return har_vol

HAR模型的实现过程包含以下关键步骤：

基于收益率平方计算日度已实现方差
构造周度（5个交易日）和月度（22个交易日）波动率分量
构建滞后预测变量矩阵
采用普通最小二乘法进行参数估计
生成波动率预测序列

模型性能比较与可视化

我们还开发了专门的可视化模块用于模型性能对比分析：

def plot_volatility_comparison(spy_data, garch_vol, gjr_vol, har_vol):
     """构建波动率模型比较图"""
     plt.figure(figsize=(15, 10))
     
     # 计算历史已实现波动率（21日滚动）
     realized_vol = np.sqrt(252) * spy_data['Returns'].rolling(window=21).std()
     
     # 统一时间序列索引
     common_index = realized_vol.index.intersection(har_vol.index)
     realized_vol = realized_vol[common_index]
     garch_vol = garch_vol[common_index]
     gjr_vol = gjr_vol[common_index]
     har_vol = har_vol[common_index]
     
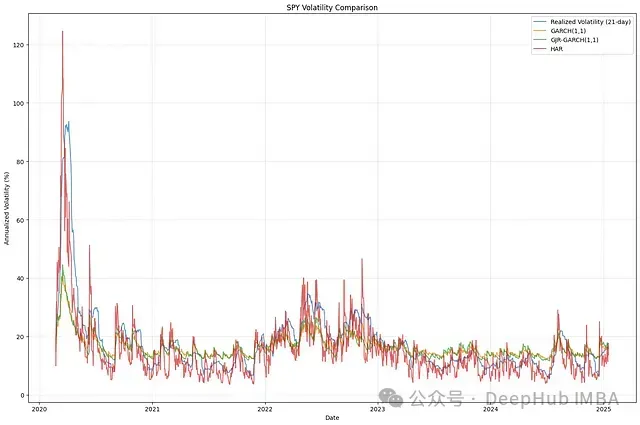
     # 绘制各模型波动率序列
     plt.plot(common_index, realized_vol, label='Realized Volatility (21-day)', alpha=0.7)
     plt.plot(common_index, garch_vol, label='GARCH(1,1)', alpha=0.7)
     plt.plot(common_index, gjr_vol, label='GJR-GARCH(1,1)', alpha=0.7)
     plt.plot(common_index, har_vol, label='HAR', alpha=0.7)

该可视化工具能够直观展示各模型对市场波动率的刻画能力及其动态特征。

模型适用性分析

各模型在实证应用中表现出不同的优势特征：

GARCH(1,1)模型：

模型结构简洁，具有较强的稳健性
能够有效捕捉波动率聚类现象
在金融业界获得广泛应用

GJR-GARCH模型：

较好地刻画了波动率的非对称响应特征
特别适用于股票市场波动率建模
在市场剧烈波动期间展现出较强的拟合优势

HAR模型：

有效捕捉波动率的长期记忆特性
模型结构具有清晰的经济学解释
在高频数据建模中表现突出

总结

波动率建模是金融风险管理中的关键环节。GARCH族模型基于严谨的统计理论基础，能够有效刻画金融收益率的典型特征；而HAR模型则提供了一种直观且实用的建模思路，在实证研究中展现出良好的预测性能。

本文通过Python实现展示了这些模型在实际市场数据中的应用方法，为更深入的金融计量分析和风险管理研究提供了实践基础。