经济时间序列中的因果关系研究已超越了传统的相关性分析范畴。本文系统性地探讨了时间序列经济数据中因果关系的识别与量化方法,涵盖从经典的格兰杰因果检验到现代因果推断技术的全方位论述。
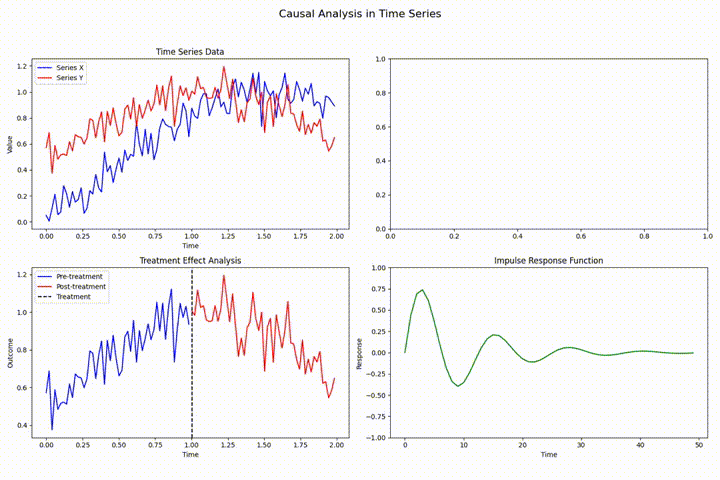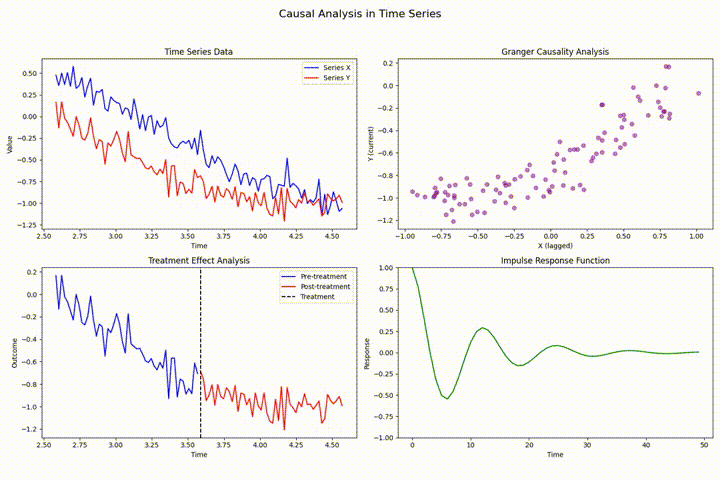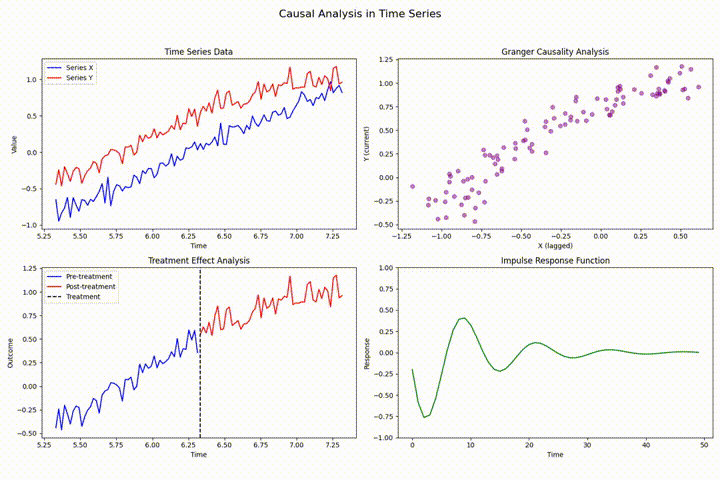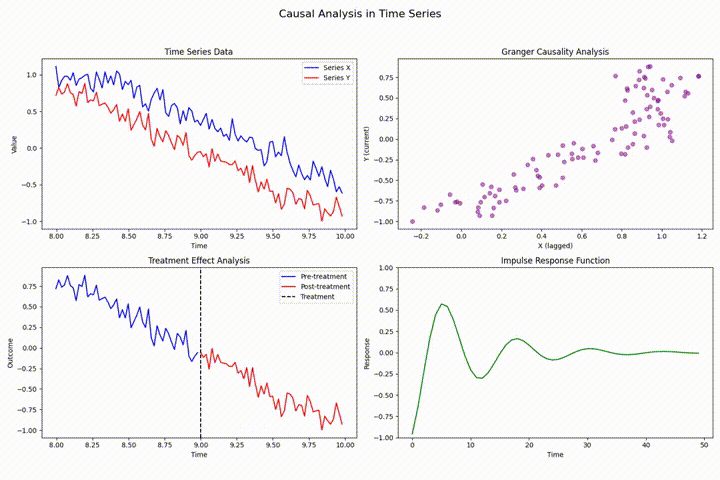
格兰杰因果检验
格兰杰因果检验是评估时间序列预测能力的基础性计量工具,用于检验一个时间序列对另一个时间序列的预测贡献。
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.tsa.stattools import grangercausalitytests
from statsmodels.tsa.api import VAR
class GrangerAnalysis:
def __init__(self, data):
self.data = data
def test_granger_causality(self, variable1, variable2, max_lags=12):
"""执行双变量格兰杰因果检验"""
data = pd.concat([self.data[variable1], self.data[variable2]], axis=1)
results = grangercausalitytests(data, maxlag=max_lags)
causality_results = pd.DataFrame(
index=range(1, max_lags + 1),
columns=['F-statistic', 'p-value']
)
for lag in range(1, max_lags + 1):
causality_results.loc[lag] = [
results[lag][0]['ssr_ftest'][0],
results[lag][0]['ssr_ftest'][1]
]
return causality_results
def plot_causality_results(self, results):
"""绘制各滞后阶的显著性检验结果"""
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.plot(results.index, results['p-value'], marker='o')
plt.axhline(y=0.05, color='r', linestyle='--', label='5% significance')
plt.xlabel('Lag Order')
plt.ylabel('p-value')
plt.title('Granger Causality Test Results')
plt.legend()
plt.show()结构向量自回归模型(SVAR)
结构向量自回归模型通过引入经济理论支持的结构性约束,对传统向量自回归(VAR)框架进行了扩展。
from statsmodels.tsa.api import VAR
class SVARModel:
def __init__(self, data):
self.data = data
self.var_model = None
self.svar_results = None
def fit(self, lags=1, A=None, B=None):
"""基于短期和长期约束拟合SVAR模型"""
self.var_model = VAR(self.data)
var_results = self.var_model.fit(lags)
if A is None:
A = np.eye(len(self.data.columns))
if B is None:
B = np.eye(len(self.data.columns))
self.svar_results = var_results.svar(A=A, B=B)
return self.svar_results
def impulse_response(self, periods=20):
"""估计脉冲响应函数"""
return self.svar_results.irf(periods=periods)
def forecast_error_variance_decomposition(self, periods=20):
"""进行预测误差方差分解"""
return self.svar_results.fevd(periods=periods)局部投影法的因果分析
局部投影法为脉冲响应估计提供了一种稳健的非参数化方法,摆脱了传统VAR模型的参数假设限制。
import statsmodels.api as sm
class LocalProjections:
def __init__(self, data):
self.data = data
def estimate_impulse_response(self, dependent_var, shock_var, controls=None, horizons=20):
"""采用局部投影法估计动态脉冲响应"""
responses = []
confidence_intervals = []
for h in range(horizons + 1):
y = self.data[dependent_var].shift(-h)
X = self.data[[shock_var]]
if controls is not None:
X = pd.concat([X, self.data[controls]], axis=1)
X = sm.add_constant(X)
valid_idx = y.notna()
y = y[valid_idx]
X = X[valid_idx]
model = sm.OLS(y, X)
results = model.fit(cov_type='HAC', cov_kwds={'maxlags': h})
responses.append(results.params[shock_var])
confidence_intervals.append(results.conf_int().loc[shock_var])
return np.array(responses), np.array(confidence_intervals)合成控制法
合成控制法通过构建最优权重组合的对照组,为反事实因果分析提供了系统性的方法论框架。
from scipy.optimize import minimize
class SyntheticControl:
def __init__(self, data, treatment_unit, control_units, treatment_period, outcome_var):
self.data = data
self.treatment_unit = treatment_unit
self.control_units = control_units
self.treatment_period = treatment_period
self.outcome_var = outcome_var
def construct_synthetic_control(self):
"""构建最优权重的合成控制单元"""
pre_treatment = self.data[self.data.index < self.treatment_period]
def objective(weights):
synthetic = np.sum([
w * pre_treatment[self.outcome_var][pre_treatment.unit == u]
for w, u in zip(weights, self.control_units)
], axis=0)
treated = pre_treatment[self.outcome_var][
pre_treatment.unit == self.treatment_unit
]
return np.mean((treated - synthetic) ** 2)
constraints = [
{'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
{'type': 'ineq', 'fun': lambda x: x}
]
result = minimize(
objective,
x0=np.ones(len(self.control_units)) / len(self.control_units),
constraints=constraints
)
return result.x多期双重差分法
双重差分法(DiD)是面板数据处理效应分析的核心计量方法,特别适用于政策评估研究。
import statsmodels.api as sm
class DynamicDiD:
def __init__(self, data):
self.data = data
def estimate_dynamic_effects(self, outcome_var, treatment_var, unit_fe=True, time_fe=True):
"""估计动态处理效应参数"""
leads_lags = range(-4, 5)
for t in leads_lags:
self.data[f'treat_t{t}'] = self.data[treatment_var].shift(-t)
formula = f"{outcome_var} ~ " + " + ".join([f"treat_t{t}" for t in leads_lags])
if unit_fe:
formula += " + EntityEffects"
if time_fe:
formula += " + TimeEffects"
model = sm.PanelOLS.from_formula(formula, data=self.data)
return model.fit(cov_type='clustered', cluster_entity=True)时间序列工具变量方法
工具变量方法通过引入满足相关性和外生性条件的工具变量,为解决内生性问题提供了可靠的计量框架。
class TSInstrumentalVariables:
def __init__(self, data):
self.data = data
def estimate_iv(self, dependent_var, endogenous_var, instrument_var, controls=None):
"""实施两阶段最小二乘估计"""
X_first = sm.add_constant(self.data[instrument_var])
if controls is not None:
X_first = pd.concat([X_first, self.data[controls]], axis=1)
first_stage = sm.OLS(self.data[endogenous_var], X_first).fit()
fitted_values = first_stage.predict()
X_second = sm.add_constant(fitted_values)
if controls is not None:
X_second = pd.concat([X_second, self.data[controls]], axis=1)
second_stage = sm.OLS(self.data[dependent_var], X_second).fit()
return first_stage, second_stage现代因果推断方法
现代因果推断方法整合了计量经济学的理论基础与机器学习的算法优势,提供了更具稳健性和可解释性的分析框架。
from sklearn.ensemble import RandomForestRegressor
class ModernCausalInference:
def __init__(self, data):
self.data = data
def double_machine_learning(self, y, d, x, ml_model=None):
"""实现双机器学习的因果参数估计"""
if ml_model is None:
ml_model = RandomForestRegressor(n_estimators=100)
ml_model.fit(self.data[x], self.data[d])
d_hat = ml_model.predict(self.data[x])
ml_model.fit(self.data[x], self.data[y])
y_hat = ml_model.predict(self.data[x])
treatment_effect = sm.OLS(
self.data[y] - y_hat,
self.data[d] - d_hat
).fit()
return treatment_effect总结
本文系统性地探讨了时间序列计量经济学中的因果推断方法体系。从经典的格兰杰因果检验入手,详细阐述了结构向量自回归模型(SVAR)、局部投影法等基础方法框架。文章深入探讨了合成控制法在构建反事实分析中的应用,以及多期双重差分法在面板数据处理效应评估中的实现。在此基础上,介绍了时间序列工具变量方法对内生性问题的处理思路,并探讨了包括双机器学习在内的现代因果推断方法。通过结合传统计量方法与现代机器学习技术,构建了一个完整的时序因果推断方法论体系,为相关领域的实证研究提供了系统的方法论指导。
































