1D 卷积层(One-Dimensional Convolutional Layer)是卷积神经网络(CNN)的基本组成部分,广泛应用于处理一维序列数据,如时间序列分析、自然语言处理、语音识别等。

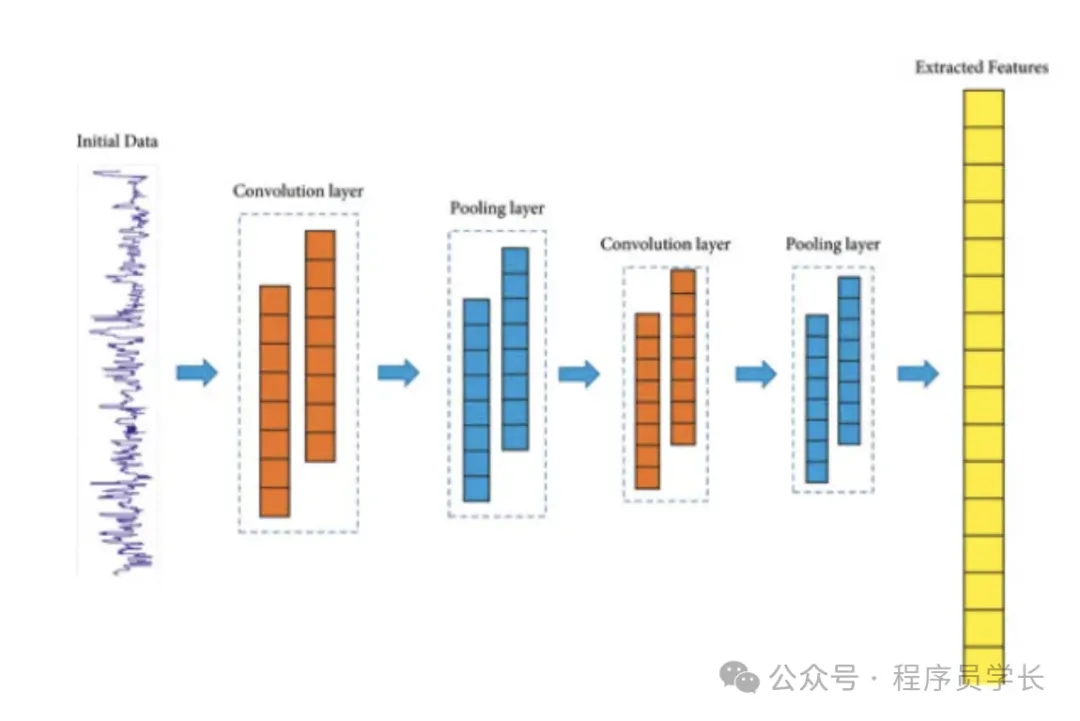
1D 卷积层是深度学习中用于处理序列数据的重要工具。它通过滑动窗口方式提取局部特征,并在多个通道间整合信息。1D 卷积为时间序列、语音信号和文本数据提供了高效的特征提取能力,同时通过参数共享和稀疏连接保持了模型的高效性和鲁棒性。
什么是1D卷积层
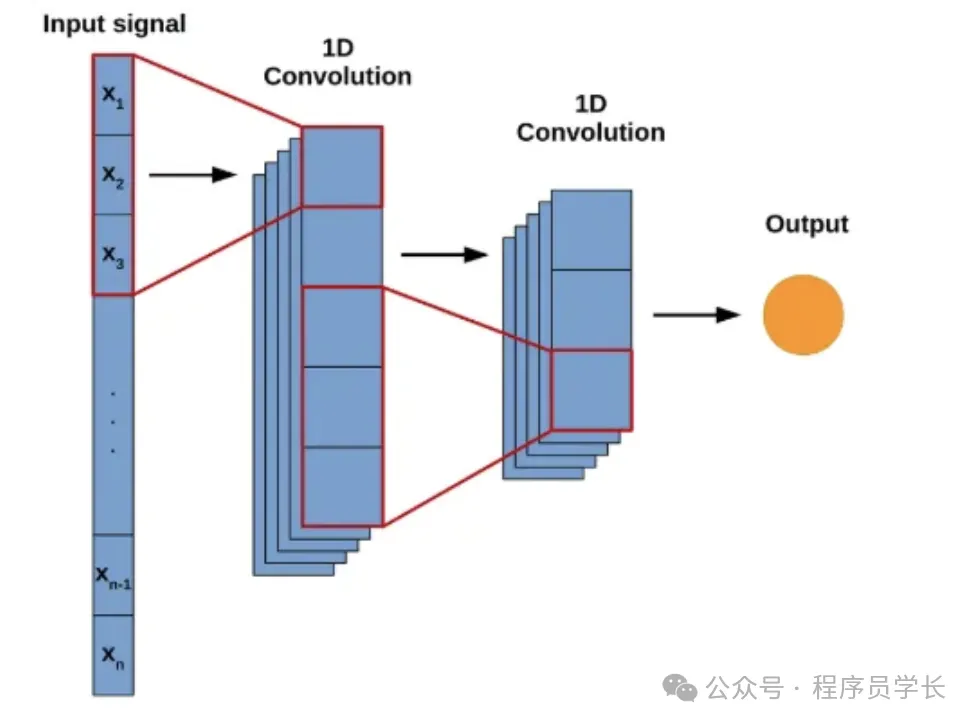
1D 卷积层通过滑动一个称为卷积核(或滤波器)的窗口,在输入序列上进行卷积操作,以提取局部特征。与2D卷积层主要用于图像处理不同,1D 卷积层主要处理一维数据,如时间序列或文本序列。
1D 卷积的基本原理
1D 卷积操作通过一个称为卷积核(或滤波器)的固定大小的窗口,在输入数据的一个维度上滑动,进行逐元素的点积运算,从而提取局部特征。
具体步骤如下:
- 输入数据:假设输入数据为一个长度为 L 的一维信号,可能具有多个通道(例如,多种传感器数据)。
- 卷积核:设定一个长度为 K 的卷积核,通常会有多个卷积核以提取不同的特征。
- 滑动窗口:卷积核在输入信号上以一定的步长(stride)滑动,每一步都与输入信号的对应部分进行点积运算,并加上一个偏置项,生成一个输出值。
- 输出特征图:滑动通过整个输入信号后,生成一个新的特征序列,称为特征图(feature map)。
关键参数
- 卷积核大小(Kernel Size)
决定了每次卷积操作覆盖的输入范围。
较大的卷积核可以捕捉更长范围的依赖关系,但计算复杂度也相应增加。 - 步长(Stride)
卷积核每次滑动的步幅。较大的步长会减少输出特征图的长度,但可能导致信息丢失。 - 填充(Padding)
在输入数据的边缘添加额外的值(通常为零),以控制输出特征图的长度。 - 通道数(Channels)
每个卷积核可以有多个输入通道,尤其在多通道输入数据(如多传感器数据)中常见。 - 激活函数(Activation Function)
通常在卷积操作后应用非线性激活函数,如 ReLU,以引入非线性能力。
1D 卷积层的应用
1D 卷积层广泛应用于以下领域
- 时间序列分析:如股票价格预测、传感器数据分析等,通过1D 卷积提取时间上的模式和趋势。
- 自然语言处理(NLP):用于文本分类、情感分析,通过提取词语序列中的局部特征。
- 音频信号处理:如语音识别、音乐分类,通过 1D 卷积提取音频信号中的特征。
- 生物信息学:如基因序列分析,通过识别 DNA/RNA 序列中的模式。
优缺点
优点
- 参数共享:卷积核在整个输入序列上共享参数,显著减少了模型的参数数量,降低了过拟合的风险。
- 局部感受野:能够有效捕捉输入序列中的局部模式和短期依赖关系,对于处理具有局部相关性的序列数据非常有效。
- 计算效率高:由于参数较少,1D卷积层的计算复杂度相对较低,适合处理长序列数据。
- 平移不变性:卷积操作对输入序列中的特定模式具有平移不变性,即模式在序列中的位置发生变化时,模型仍能有效识别。
- 灵活性强:可以通过堆叠多个卷积层或调整卷积核大小,捕捉不同尺度的特征。
缺点
- 长距离依赖捕捉能力有限
虽然堆叠多个卷积层可以扩展感受野,但在捕捉序列中长距离依赖关系时,1D卷积层可能不如循环神经网络(RNN)或自注意力机制(如Transformer)有效。 - 特征提取的局限性
在某些复杂任务中,1D卷积层提取的特征可能不足以捕捉所有重要的信息,需要结合其他模型或技术进行增强。
案例分享
以下是分别使用 PyTorch 和 TensorFlow 实现 1D 卷积神经网络来进行时间序列预测的示例代码。
PyTorch 实现
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
# 生成示例时间序列数据
def generate_sine_wave(seq_length, num_samples):
x = np.linspace(0, 4 * np.pi, seq_length)
data = np.array([np.sin(x + np.random.uniform(0, 2 * np.pi)) for _ in range(num_samples)])
return data
# 数据准备
seq_length = 50 # 输入序列长度
num_samples = 1000 # 样本数
prediction_length = 1 # 预测的未来步数
data = generate_sine_wave(seq_length + prediction_length, num_samples)
# 划分数据:输入和目标
X = data[:, :-prediction_length] # 输入序列
y = data[:, -prediction_length:] # 目标值
# 转为 PyTorch 张量
X = torch.tensor(X, dtype=torch.float32).unsqueeze(1) # 添加通道维度 (batch, channel, seq_length)
y = torch.tensor(y, dtype=torch.float32)
# 划分训练和测试集
train_size = int(0.8 * len(X))
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y[:train_size], y[train_size:]
# 检查数据形状
print("训练集输入形状:", X_train.shape) # (batch_size, channels, seq_length)
print("训练集目标形状:", y_train.shape) # (batch_size, prediction_length)
# 定义 1D 卷积预测模型
class Conv1DPredictor(nn.Module):
def __init__(self, input_channels, output_size, kernel_size=3):
super(Conv1DPredictor, self).__init__()
self.conv1 = nn.Conv1d(in_channels=input_channels, out_channels=16, kernel_size=kernel_size, padding=1)
self.conv2 = nn.Conv1d(in_channels=16, out_channels=32, kernel_size=kernel_size, padding=1)
self.fc = nn.Linear(32 * seq_length, output_size) # 全连接层,用于生成预测结果
def forward(self, x):
x = torch.relu(self.conv1(x)) # 第一层卷积 + 激活
x = torch.relu(self.conv2(x)) # 第二层卷积 + 激活
x = x.view(x.size(0), -1) # 展平
x = self.fc(x) # 全连接层输出
return x
# 初始化模型
model = Conv1DPredictor(input_channels=1, output_size=prediction_length)
criterion = nn.MSELoss() # 损失函数
optimizer = optim.Adam(model.parameters(), lr=0.001) # 优化器
# 训练模型
num_epochs = 50
train_losses = []
for epoch in range(num_epochs):
model.train()
optimizer.zero_grad()
output = model(X_train) # 前向传播
loss = criterion(output, y_train) # 计算损失
loss.backward() # 反向传播
optimizer.step() # 更新权重
train_losses.append(loss.item())
if (epoch + 1) % 10 == 0:
print(f"Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}")
# 测试模型
model.eval()
with torch.no_grad():
y_pred = model(X_test)
test_loss = criterion(y_pred, y_test)
print(f"测试集损失: {test_loss.item():.4f}")
# 可视化结果
plt.figure(figsize=(10, 5))
plt.plot(y_test.numpy()[:50], label="True Values")
plt.plot(y_pred.numpy()[:50], label="Predictions")
plt.legend()
plt.title("Time Series Prediction")
plt.show()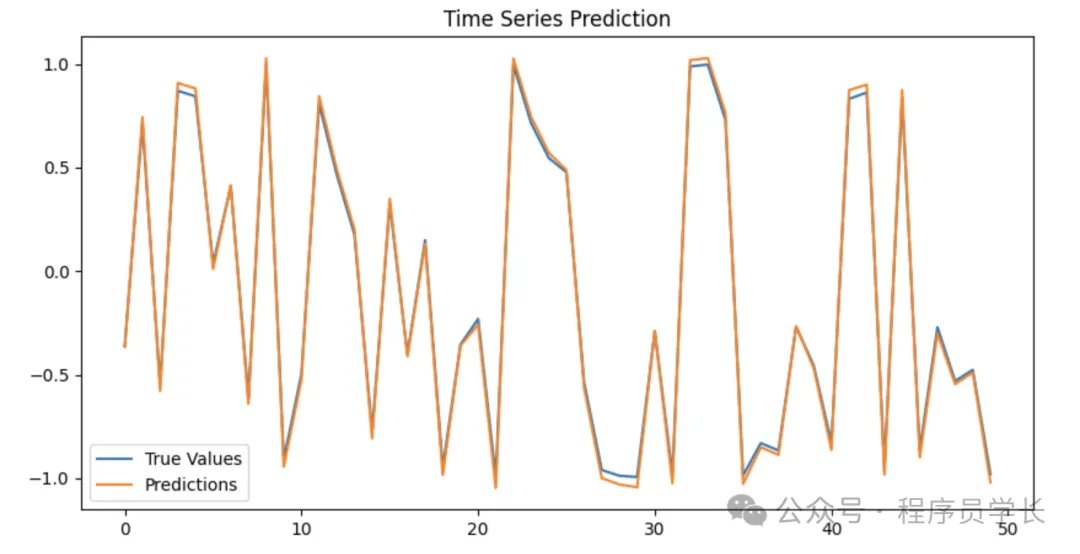
TensorFlow 实现
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv1D, Dense, Flatten
from tensorflow.keras.optimizers import Adam
import matplotlib.pyplot as plt
# 生成示例时间序列数据
def generate_sine_wave(seq_length, num_samples):
x = np.linspace(0, 4 * np.pi, seq_length)
data = np.array([np.sin(x + np.random.uniform(0, 2 * np.pi)) for _ in range(num_samples)])
return data
# 数据准备
seq_length = 50 # 输入序列长度
num_samples = 1000 # 样本数
prediction_length = 1 # 预测未来步数
data = generate_sine_wave(seq_length + prediction_length, num_samples)
# 划分数据:输入和目标
X = data[:, :-prediction_length] # 输入序列
y = data[:, -prediction_length:] # 目标值
# 划分训练集和测试集
train_size = int(0.8 * len(X))
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y[:train_size], y[train_size:]
# 扩展维度以适配 Conv1D 输入格式
X_train = X_train[..., np.newaxis] # 转换为 (batch_size, seq_length, channels)
X_test = X_test[..., np.newaxis]
# 检查数据形状
print("训练集输入形状:", X_train.shape) # (batch_size, seq_length, channels)
print("训练集目标形状:", y_train.shape) # (batch_size, prediction_length)
# 构建 1D 卷积预测模型
model = Sequential([
Conv1D(filters=16, kernel_size=3, activatinotallow='relu', padding='same', input_shape=(seq_length, 1)),
Conv1D(filters=32, kernel_size=3, activatinotallow='relu', padding='same'),
Flatten(),
Dense(10, activatinotallow='relu'),
Dense(prediction_length) # 输出层
])
# 编译模型
model.compile(optimizer=Adam(learning_rate=0.001), loss='mse')
# 训练模型
history = model.fit(X_train, y_train, epochs=50, batch_size=32, validation_split=0.2, verbose=1)
# 测试模型
test_loss = model.evaluate(X_test, y_test, verbose=0)
print(f"测试集损失: {test_loss:.4f}")
# 预测并可视化
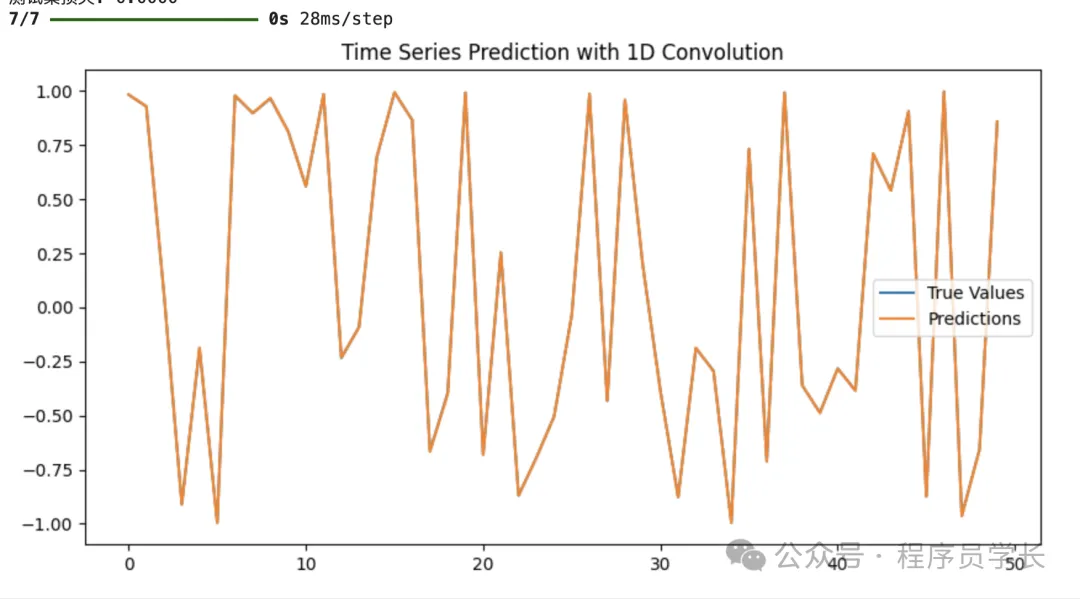
y_pred = model.predict(X_test)
plt.figure(figsize=(10, 5))
plt.plot(y_test[:50], label="True Values")
plt.plot(y_pred[:50], label="Predictions")
plt.legend()
plt.title("Time Series Prediction with 1D Convolution")
plt.show()