C#中的圆弧插补算法详解：GDI+图形绘制与运动控制

using System;
using System.Drawing;
using System.Windows.Forms;
using System.Drawing.Drawing2D;
using Timer = System.Windows.Forms.Timer;

namespace AppCircularInterpolation
{
    public partial class Form1 : Form
    {
        // 圆弧插补关键参数  
        private float centerX, centerY;  // 圆心坐标  
        private float radius;            // 圆半径  
        private float startAngle;        // 起始角度  
        private float endAngle;          // 结束角度  
        private bool clockwise;          // 旋转方向  

        // 动画相关参数  
        private Timer animationTimer;
        private float currentAnimationProgress = 0f;
        private const int AnimationDuration = 3000; // 动画持续时间（毫秒）  
        private DateTime animationStartTime;

        public Form1()
        {
            InitializeComponent();
            this.DoubleBuffered = true;
            InitializeInterpolationParameters();
            InitializeAnimation();
        }

        private void InitializeInterpolationParameters()
        {
            // 设置圆弧基本参数  
            centerX = 250;
            centerY = 250;
            radius = 200;
            startAngle = 0;
            endAngle = 270;
            clockwise = true;
        }

        private void InitializeAnimation()
        {
            // 设置动画计时器  
            animationTimer = new Timer();
            animationTimer.Interval = 16; // 约60帧/秒  
            animationTimer.Tick += AnimationTimer_Tick;
        }

        // 启动动画  
        private void StartAnimation()
        {
            currentAnimationProgress = 0f;
            animationStartTime = DateTime.Now;
            animationTimer.Start();
        }

        // 动画计时器事件  
        private void AnimationTimer_Tick(object sender, EventArgs e)
        {
            // 计算动画进度  
            TimeSpan elapsed = DateTime.Now - animationStartTime;
            currentAnimationProgress = Math.Min(1f, (float)elapsed.TotalMilliseconds / AnimationDuration);

            // 触发重绘  
            Invalidate();

            // 动画结束  
            if (currentAnimationProgress >= 1f)
            {
                animationTimer.Stop();
            }
        }

        // 圆弧插补核心算法（带动画进度）- 补差球  
        private PointF CalculateInterpolationBallPoint()
        {
            float currentEndAngle = startAngle + (endAngle - startAngle) * currentAnimationProgress;
            float interpolationAngle = startAngle + (currentEndAngle - startAngle) * currentAnimationProgress;
            float angleRad = interpolationAngle * (float)Math.PI / 180;

            return new PointF(
                centerX + radius * (float)Math.Cos(angleRad),
                centerY + radius * (float)Math.Sin(angleRad)
            );
        }

        // 匀速小球坐标计算  
        private PointF CalculateUniformMotionBallPoint()
        {
            float uniformAngle = startAngle + (endAngle - startAngle) * currentAnimationProgress;
            float angleRad = uniformAngle * (float)Math.PI / 180;

            return new PointF(
                centerX + radius * (float)Math.Cos(angleRad),
                centerY + radius * (float)Math.Sin(angleRad)
            );
        }

        // 圆弧插补核心算法（带动画进度）  
        private PointF[] CalculateArcPoints(int interpolationSteps)
        {
            PointF[] points = new PointF[interpolationSteps + 1];
            float currentEndAngle = startAngle + (endAngle - startAngle) * currentAnimationProgress;

            for (int i = 0; i <= interpolationSteps; i++)
            {
                // 计算当前插补角度  
                float currentAngle = startAngle +
                    (currentEndAngle - startAngle) * i / interpolationSteps;

                // 角度转换为弧度  
                float angleRad = currentAngle * (float)Math.PI / 180;

                // 计算圆周上的坐标点  
                points[i] = new PointF(
                    centerX + radius * (float)Math.Cos(angleRad),
                    centerY + radius * (float)Math.Sin(angleRad)
                );
            }

            return points;
        }

        // 绘制圆弧轨迹  
        protected override void OnPaint(PaintEventArgs e)
        {
            base.OnPaint(e);
            Graphics g = e.Graphics;
            g.SmoothingMode = SmoothingMode.AntiAlias;

            // 获取插补点  
            PointF[] interpolationPoints = CalculateArcPoints(100);

            // 绘制圆弧轨迹  
            using (Pen arcPen = new Pen(Color.Blue, 2))
            {
                g.DrawLines(arcPen, interpolationPoints);
            }

            // 绘制圆心和起止点  
            using (SolidBrush brush = new SolidBrush(Color.Red))
            {
                g.FillEllipse(brush, centerX - 5, centerY - 5, 10, 10);
            }

            // 绘制补差球（红色）  
            PointF interpolationBallPoint = CalculateInterpolationBallPoint();
            using (SolidBrush interpolationBallBrush = new SolidBrush(Color.Red))
            {
                g.FillEllipse(interpolationBallBrush, interpolationBallPoint.X - 10, interpolationBallPoint.Y - 10, 20, 20);
            }

            // 绘制匀速小球（绿色）  
            PointF uniformMotionBallPoint = CalculateUniformMotionBallPoint();
            using (SolidBrush uniformMotionBallBrush = new SolidBrush(Color.Green))
            {
                g.FillEllipse(uniformMotionBallBrush, uniformMotionBallPoint.X - 10, uniformMotionBallPoint.Y - 10, 20, 20);
            }

            // 绘制动画进度文本  
            using (Font font = new Font("Arial", 12))
            using (SolidBrush textBrush = new SolidBrush(Color.Black))
            {
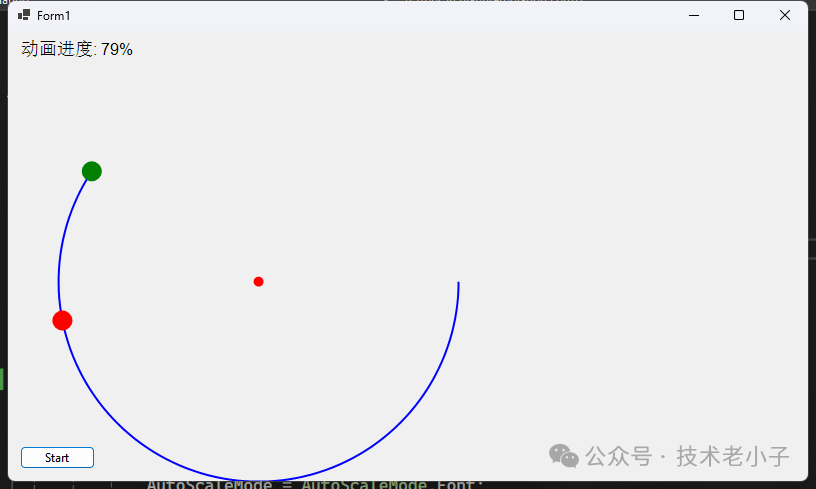
                g.DrawString($"动画进度: {currentAnimationProgress:P0}", font, textBrush, 10, 10);
            }
        }

        // 添加启动动画的按钮事件  
        private void btnStart_Click(object sender, EventArgs e)
        {
            StartAnimation();
        }
    }
}