江中华,浙江大学软件学院硕士生二年级,导师为张圣宇老师。研究方向为大小模型端云协同计算。张圣宇,浙江大学平台「百人计划」研究员。研究方向包括大小模型端云协同计算,多媒体分析与数据挖掘。
随着机器学习技术的发展,隐私保护和分布式优化的需求日益增长。联邦学习作为一种分布式机器学习技术,允许多个客户端在不共享数据的情况下协同训练模型,从而有效地保护了用户隐私。然而,每个客户端的数据可能各不相同,有的数据量大,有的数据量小;有的数据特征丰富,有的数据特征单一。这种数据的异质性和不平衡性(Non-IID)会导致一个问题:本地训练的客户模型忽视了全局数据中明显的更广泛的模式,聚合的全局模型可能无法准确反映所有客户端的数据分布,甚至可能出现「辛普森悖论」—— 多端各自数据分布趋势相近,但与多端全局数据分布趋势相悖。
为了解决这一问题,来自浙江大学人工智能研究所的研究团队提出了 FedCFA,一个基于反事实学习的新型联邦学习框架。
FedCFA 引入了端侧反事实学习机制,通过在客户端本地生成与全局平均数据对齐的反事实样本,缓解端侧数据中存在的偏见,从而有效避免模型学习到错误的特征 - 标签关联。该研究已被 AAAI 2025 接收。

- 论文标题:FedCFA: Alleviating Simpson’s Paradox in Model Aggregation with Counterfactual Federated Learning
- 论文链接:https://arxiv.org/abs/2412.18904
- 项目地址:https://github.com/hua-zi/FedCFA
辛普森悖论
辛普森悖论(Simpson's Paradox)是一种统计现象。简单来说,当你把数据分成几个子组时,某些趋势或关系在每个子组中表现出一致的方向,但在整个数据集中却出现了相反的趋势。
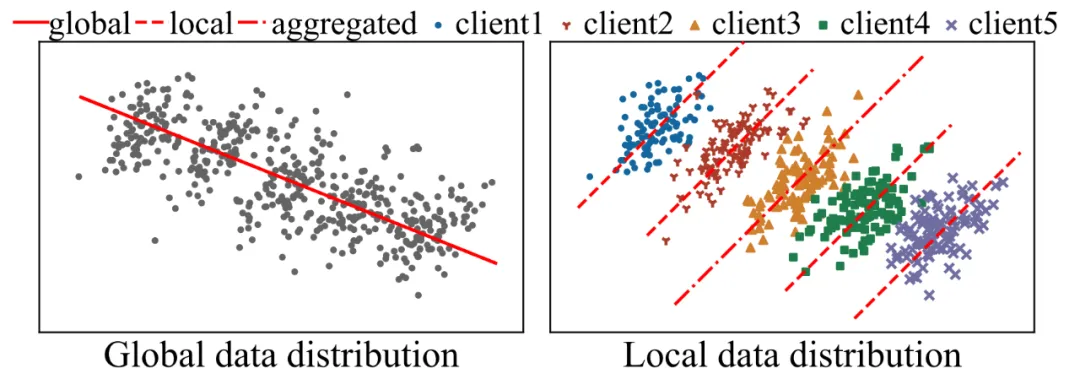
图 1:辛普森悖论。在全局数据集上观察到的趋势在子集上消失 / 逆转,聚合的全局模型无法准确反映全局数据分布
在联邦学习中,辛普森悖论可能会导致全局模型无法准确捕捉到数据的真实分布。例如,某些客户端的数据中存在特定的特征 - 标签关联(如颜色与动物种类的关系),而这些关联可能在全局数据中并不存在。因此,直接将本地模型汇聚成全局模型可能会引入错误的学习结果,影响模型的准确性。
如图 2 所示。考虑一个用于对猫和狗图像进行分类的联邦学习系统,涉及具有不同数据集的两个客户端。客户端 i 的数据集主要包括白猫和黑狗的图像,客户端 j 的数据集包括浅灰色猫和棕色狗的图像。对于每个客户端而言,数据集揭示了类似的趋势:浅色动物被归类为「猫」,而深色动物被归类为「狗」。这导致聚合的全局模型倾向于将颜色与类别标签相关联并为颜色特征分配更高的权重。然而,全局数据分布引入了许多不同颜色的猫和狗的图像(例如黑猫和白狗),与聚合的全局模型相矛盾。在全局数据上训练的模型可以很容易地发现动物颜色与特定分类无关,从而减少颜色特征的权重。

图 2:FedCFA 可以生成客户端本地不存在的反事实样本,防止模型学习到不正确的特征 - 标签关联。
反事实学习
反事实(Counterfactual)就像是「如果事情发生了另一种情况,结果会如何?」 的假设性推理。在机器学习中,反事实学习通过生成与现实数据不同的虚拟样本,来探索不同条件下的模型行为。这些虚拟样本可以帮助模型更好地理解数据中的因果关系,避免学习到虚假的关联。
反事实学习的核心思想是通过对现有数据进行干预,生成新的样本,这些样本反映了某种假设条件下的情况。例如,在图像分类任务中,我们可以改变图像中的某些特征(如颜色、形状等),生成与原图不同的反事实样本。通过让模型学习这些反事实样本,可以提高模型对真实数据分布的理解,避免过拟合局部数据的特点。
反事实学习广泛应用于推荐系统、医疗诊断、金融风险评估等领域。在联邦学习中,反事实学习可以帮助缓解辛普森悖论带来的问题,使全局模型更准确地反映整体数据的真实分布。
FedCFA 框架简介
为了解决联邦学习中的辛普森悖论问题,FedCFA 框架通过在客户端生成与全局平均数据对齐的反事实样本,使得本地数据分布更接近全局分布,从而有效避免了错误的特征 - 标签关联。
如图 2 所示,通过反事实变换生成的反事实样本使局部模型能够准确掌握特征 - 标签关联,避免局部数据分布与全局数据分布相矛盾,从而缓解模型聚合中的辛普森悖论。从技术上讲,FedCFA 的反事实模块,选择性地替换关键特征,将全局平均数据集成到本地数据中,并构建用于模型学习的反事实正 / 负样本。具体来说,给定本地数据,FedCFA 识别可有可无 / 不可或缺的特征因子,通过相应地替换这些特征来执行反事实转换以获得正 / 负样本。通过对更接近全局数据分布的反事实样本进行对比学习,客户端本地模型可以有效地学习全局数据分布。然而,反事实转换面临着从数据中提取独立可控特征的挑战。一个特征可以包含多种类型的信息,例如动物图像的一个像素可以携带颜色和形状信息。为了提高反事实样本的质量,需要确保提取的特征因子只包含单一信息。因此,FedCFA 引入因子去相关损失,直接惩罚因子之间的相关系数,以实现特征之间的解耦。

全局平均数据集的构建
为了构建全局平均数据集,FedCFA 利用了中心极限定理(Central Limit Theorem, CLT)。根据中心极限定理,若从原数据集中随机抽取的大小为 n 的子集平均值记为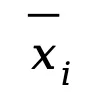 ,则当 n 足够大时,
,则当 n 足够大时,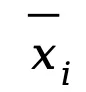 的分布趋于正态分布,其均值为 μ,方差
的分布趋于正态分布,其均值为 μ,方差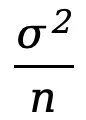 ,即:
,即: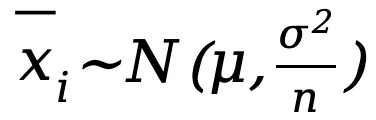 ,其中 µ 和
,其中 µ 和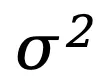 是原始数据集的期望和方差。
是原始数据集的期望和方差。
当 n 较小时, 能更精细地捕捉数据集的局部特征与变化,特别是在保留数据分布尾部和异常值附近的细节方面表现突出。相反,随着 n 的增大,
能更精细地捕捉数据集的局部特征与变化,特别是在保留数据分布尾部和异常值附近的细节方面表现突出。相反,随着 n 的增大, 的稳定性显著提升,其方差明显减小,从而使其作为总体均值 𝜇 的估计更为稳健可靠,对异常值的敏感度大幅降低。此外,在联邦学习等分布式计算场景中,为了实现通信成本的有效控制,选择较大的 n 作为样本量被视为一种优化策略。
的稳定性显著提升,其方差明显减小,从而使其作为总体均值 𝜇 的估计更为稳健可靠,对异常值的敏感度大幅降低。此外,在联邦学习等分布式计算场景中,为了实现通信成本的有效控制,选择较大的 n 作为样本量被视为一种优化策略。
基于上述分析,FedCFA 按照以下步骤构建一个大小为 B 的全局平均数据集,以此近似全局数据分布:
1.本地平均数据集计算:每个客户端将其本地数据集随机划分为 B 个大小为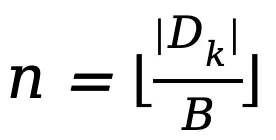 的子集
的子集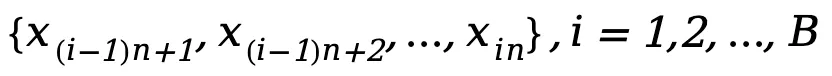 ,其中
,其中 为客户端数据集大小。对于每个子集,计算其平均值
为客户端数据集大小。对于每个子集,计算其平均值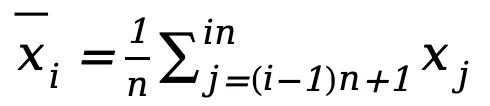 。由此,客户端能够生成本地平均数据集
。由此,客户端能够生成本地平均数据集 以近似客户端原始数据的分布。
以近似客户端原始数据的分布。
2.全局平均数据集计算:服务器端则负责聚合来自多个客户端的本地平均数据,并采用相同的方法计算出一个大小为 B 的全局平均数据集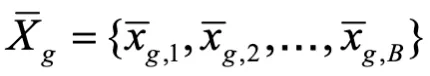 ,该数据集近似了全局数据的分布。对于标签 Y,FedCFA 采取相同的计算策略,生成其对应的全局平均数据标签
,该数据集近似了全局数据的分布。对于标签 Y,FedCFA 采取相同的计算策略,生成其对应的全局平均数据标签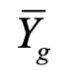 。最终得到完整的全局平均数据集
。最终得到完整的全局平均数据集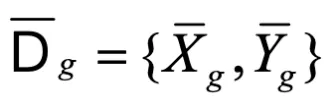
反事实变换模块
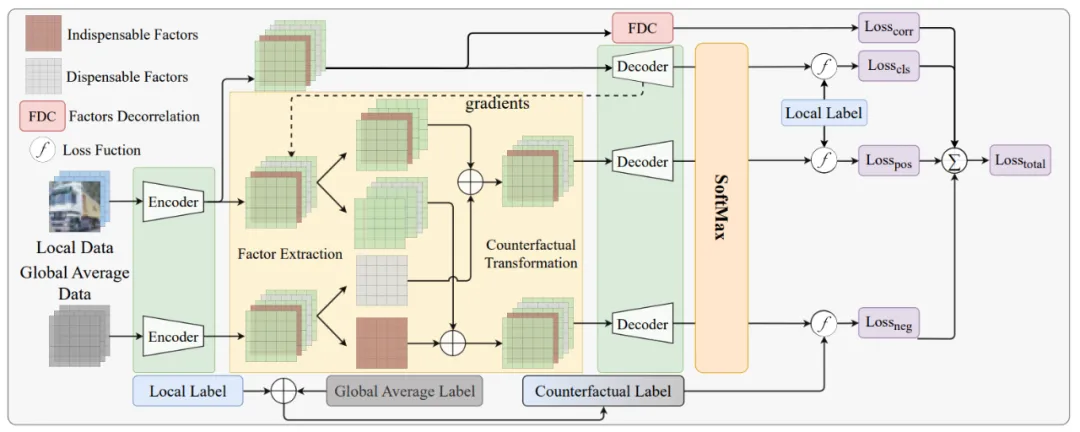
图 3:FedCFA 中的本地模型训练流程
FedCFA 中的本地模型训练流程如图 3 所示。反事实变换模块的主要任务是在端侧生成与全局数据分布对齐的反事实样本:
- 特征提取:使用编码器(Encoder)从原始数据中提取特征因子
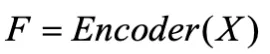 。
。 - 选择关键特征:计算每个特征在解码器(Decoder)输出层的梯度,选择梯度小 / 大的 topk 个特征因子作为可替换的因子,使用
 将选定的小 / 大梯度因子设置为零,以保留需要的因子
将选定的小 / 大梯度因子设置为零,以保留需要的因子 - 生成反事实样本:用 Encoder 提取的全局平均数据特征替换可替换的特征因子,得到反事实正 / 负样本,对于正样本,标签不会改变。对于负样本,使用加权平均值来生成反事实标签:
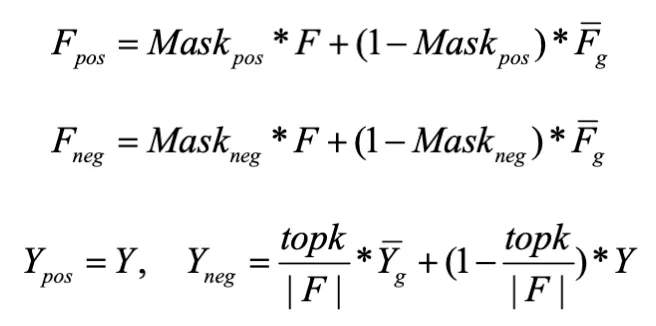
因子去相关损失
同一像素可能包含多个数据特征。例如,在动物图像中,一个像素可以同时携带颜色和外观信息。为了提高反事实样本的质量,FedCFA 引入了因子去相关(Factor Decorrelation, FDC)损失,用于减少提取出的特征因子之间的相关性,确保每个特征因子只携带单一信息。具体来说,FDC 损失通过计算每对特征之间的皮尔逊相关系数(Pearson Correlation Coefficient)来衡量特征的相关性,并将其作为正则化项加入到总损失函数中。
给定一批数据,用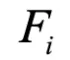 来表示第 i 个样本的所有因子。
来表示第 i 个样本的所有因子。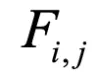 表示第 i 个样本的第 j 个因子。将同一批次中每个样本的相同指标 j 的因子视为一组变量
表示第 i 个样本的第 j 个因子。将同一批次中每个样本的相同指标 j 的因子视为一组变量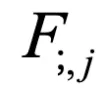 。最后,使用每对变量的 Pearson 相关系数绝对值的平均值作为 FDC 损失:
。最后,使用每对变量的 Pearson 相关系数绝对值的平均值作为 FDC 损失:
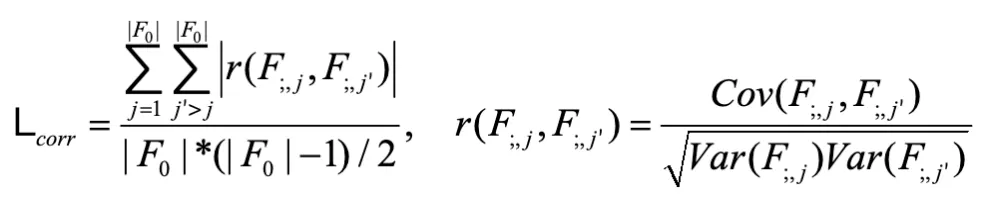
其中 Cov (・) 是协方差计算函数,Var (・) 是方差计算函数。最终的总损失为:
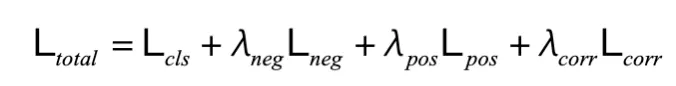
实验结果
实验采用两个指标:500 轮后的全局模型精度 和 达到目标精度所需的通信轮数,来评估 FedCFA 的性能。
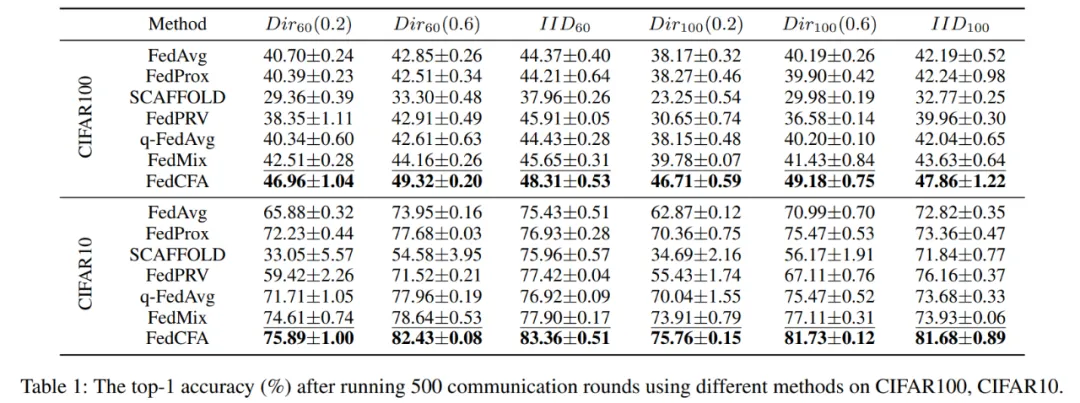
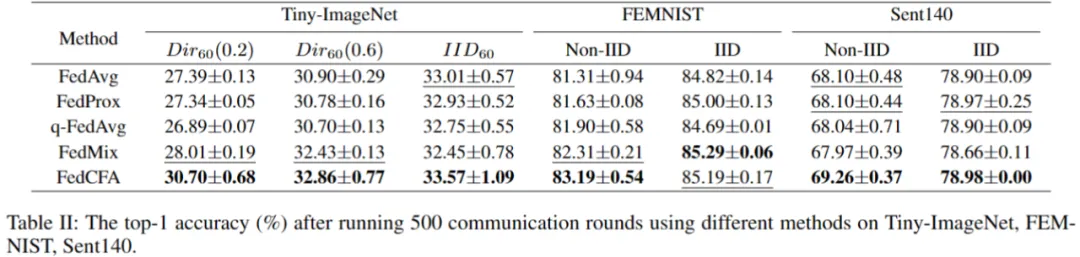

实验基于 MNIST 构建了一个具有辛普森悖论的数据集。具体来说,给 1 和 7 两类图像进行上色,并按颜色深浅划分给 5 个客户端。每个客户端的数据中,数字 1 的颜色都比数字 7 的颜色深。随后预训练一个准确率 96% 的 MLP 模型,作为联邦学习模型初始模型。让 FedCFA 与 FedAvg,FedMix 两个 baseline 作为对比,在该数据集上进行训练。如图 5 所示,训练过程中,FedAvg 和 FedMix 均受辛普森悖论的影响,全局模型准确率下降。而 FedCFA 通过反事实转换,可以破坏数据中的虚假的特征 - 标签关联,生成反事实样本使得本地数据分布靠近全局数据分布,模型准确率提升。

图 4: 具有辛普森悖论的数据集
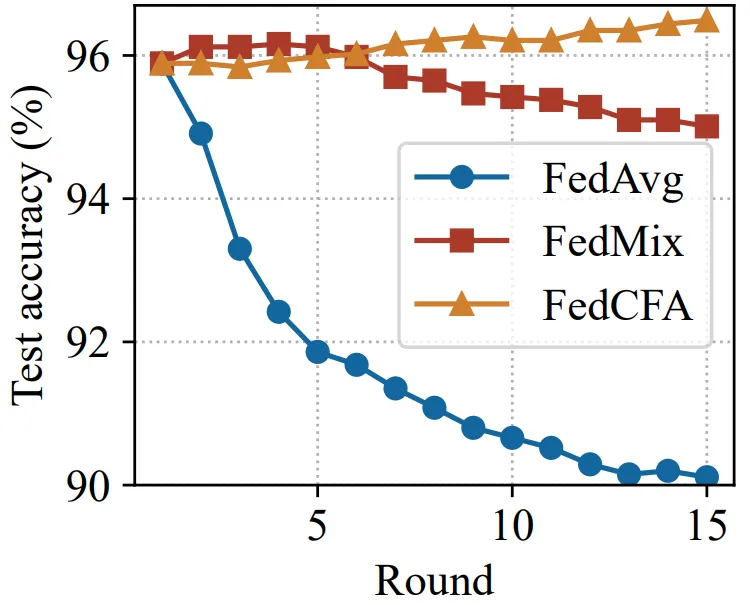
图 5: 在辛普森悖论数据集上的全局模型 top-1 准确率
消融实验

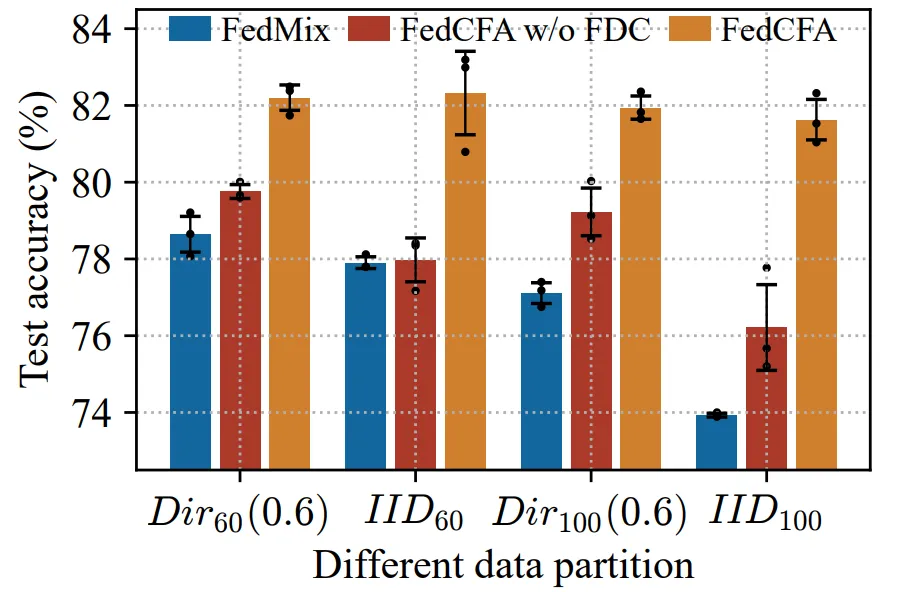
图 6:因子去相关 (FDC) 损失的消融实验






































