7B参数的Qwen2.5数学推理表现超过o1-preview,这是怎么做到的?!
靠的就是MSRA最新的创新算法,rStar-Math。
通过代码增强CoT、蒙特卡洛树搜索(MCTS)等,rStar-Math能让小·大模型在不依赖蒸馏教师模型的情况下,通过多轮自我进化的深度思维,掌握数学推理。

并且战功赫赫:
在美国数学竞赛AIME 2024测试中,rStar-Math平均解决了53.3%的难题(OpenAI o1-preview为44.6%),打败所有其它开源大模型,一举成为最聪明的高中生数学top20%。
在MATH基准测试中,rStar-Math将阿里开源大模型Qwen2.5-Math-7B的准确率,从58.8%拉升到90.0%;Qwen2.5-Math-1.5B的准确率从51.2%拉升到87.8%;Phi3-mini-3.8B的准确率从41.4%提高到86.4%
——这些成绩全部全部超过了OpenAI o1-preview。
就说牛不牛吧!
小声说,微软最近有一股在小·大模型圈子里重拳出击的态势:昨天刚开源了目前最强的小·大模型,14B的phi-4;今天又推出了rStar-Math,论文中直指其面向小语言模型(SLM)。
这个趋势刚有点苗头,立刻引得全网讨论连连。
有网友不禁开始猜测:
咱就是说,有没有一种可能,在固定计算预算的情况下,小·大模型其实在某些推理问题上,它就是抢过大模型呢?
rStar - Math怎么做到的?
Let’s 提问:
让小语言模型能和o1的数学推理能力相媲美甚至超越,且无需从高级教师模型中蒸馏,它怎么做到的?
MSRA在论文中表示,这是通过蒙特卡洛树搜索(MCTS)进行深度思考来实现的,并且,其中一个数学策略小模型在基于小模型的过程奖励模型的指导下执行测试时搜索。
目前,业界普遍依赖自然语言生成的推理步骤来提升数学推理模型的能力。
这种方法很直给,但其关键在于训练一个强大的策略模型来生成解决方案步骤,还需要训练一个可靠的奖励模型来进行准确评估。
然而上述两个模型都依赖于高质量的训练数据。
众所周知的坏消息是,高质量的数学推理数据在现在是非常非常稀缺的,同时高质量的合成数据也存在一定bug。
而且实验过程表明,它容易造成许多不相关、不必要的步骤,或产生错误。
当这种浪费和失误出现在复杂的数学问题中时,一般很难被察觉。
现有的办法,比如基于蒸馏的数据合成方法来训练策略模型(如扩大GPT-4蒸馏的CoT数据),已经明显的出现回报递减,且最终展现的能力无法超过其他教师模型。
与此同时,截至今天,训练可靠的PRM(Process Reward Model,过程奖励模型)进行数学推理仍然是一个悬而未决的问题。
MSRA此次推出的rStar-Math,就引入了三项创新方法,来应对训练两个小模型的挑战:
- 代码增强CoT数据合成方法
- 过程奖励模型训练方法
- 四轮自我思维深度进化
咱展开来说说~
代码增强CoT数据合成方法
rStar-Math选择使用代码增强CoT来解决上述难题。
该方法执行广泛的MCTS部署,从而生成具有自我注释的MCTS Q值的逐步验证推理轨迹。
具体来说,一个数学问题的求解,会在MCTS内被分解为多步生成。
模型在生成每一步推理时,作为策略模型的哪个SLM会对候选节点进行采样,不仅生成这一步的CoT思维脸解释,还生成相对应的Python代码。
为了验证生成质量,只有成功执行Python代码的节点才会被保留,从而减少中间步骤的错误,确保每一步推理的正确性。

在此基础上,为了进一步确保推理步骤的质量,rStar-Math使用了MCTS来生成逐步推理轨迹(用来分解复杂的数学问题为多个单步生成任务)。
大量的MCTS回滚会根据每个中间步骤对最终正确答案的贡献,自动为其分配一个Q值。
有助于产生更多导致正确答案的轨迹的步骤将被赋予更高的Q值,并被认为具有更高的质量。
这确保了SLM生成的推理轨迹,是由正确、高质量的中间步骤组成的。
过程奖励模型训练方法
现阶段,多数大模型在解决推理数学问题时,都面临一个问题:
无法无法提供细粒度的步骤级反馈,以帮助其在推理过程中做出更优的选择。
尽管使用了广泛的MCTS部署,仍会出现Q值不够精确的情况,这就导致无法对每个推理步骤进行评分。
为此,rStar-Math通过引入用于训练充当过程偏好模型(PPM,Process Preference Model)的SLM,来可靠地为每个数学推理步骤预测奖励标签。
PPM的核心思想,是通过构建步骤级的正负偏好对来训练模型,而不是直接依赖于精确的步骤级评分。
它根据Q值为每个步骤构建偏好对,并使用成对排名损失来优化PPM对每个推理步骤的分数预测,实现可靠的标记。
如上所述,Q值虽然不精准、含噪声,但PPM可以利用它,可靠地区分正(正确)步骤和负(不相关 / 错误)步骤。
四轮自我思维深度进化
由于SLM能力较大模型更弱,团队设计了四轮自我思维深度进化,以逐步生成更高质量的数据,并通过更具挑战性的数学问题扩展训练集。
值得注意的是,团队首先选择了一个包含747k个数学问题的开源数据集。
但在每一轮中,研究团队没有使用747k数学数据集中的原始解决方案,而是进行了广泛的MCTS部署——
四轮中的每一轮,都使用MCTS生成逐步验证的推理轨迹,然后将其用于训练新策略SLM和PPM;然后又在下一轮中应用新模型,以生成更高质量的训练数据。
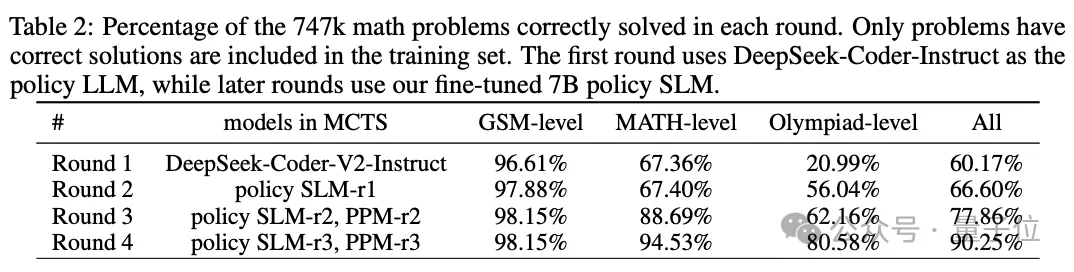
四轮自我思维深度进化具体如下。
第一轮:
通过监督微调对基础模型进行初步改进,为后续的自我进化奠定基础。
改进后的模型表示为SLM-r1。
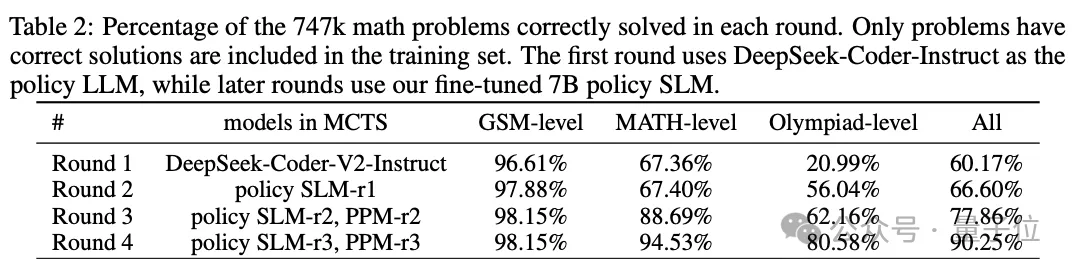
如表2所示,研究人员使用DeepSeek-Coder-V2-Instruct (236B)运行MCTS来收集SFT数据。
由于本轮没有可用的奖励模型,研究者对Q值使用终端引导的注释,并将MCTS限制为8次推出,以提高效率。
为了获得正确的解决方案,团队选择具有最高平均Q值的前2条轨迹作为SFT数据。
同时,团队在这一轮中也训练了PPM-r1。
这一轮的关键在于生成高质量的初始训练数据,并利用这些数据对基础模型进行微调。
第二轮:
训练可靠的PPM-r2,通过PPM显著提升模型推理能力。
在这一轮中,随着策略模型更新到7B SLM-r1,团队进行了广泛的MCTS部署,以获得更可靠的Q值注释;除此之外,还训练了第一个可靠的奖励模型PPM-r2。
具体来说,研究团队为每个问题执行16次MCTS部署。由此产生的逐步验证推理轨迹表明,质量和Q值精度都有了显著提高。
如表 4 所示,PPM-r2明显比bootstrap轮次更有效。
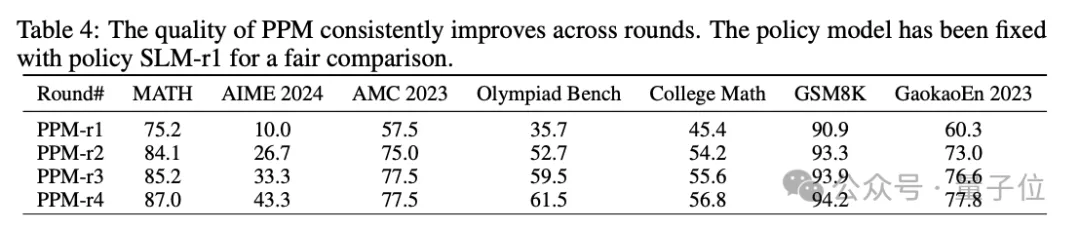
此外,如表3所示,策略模型SLM-r2也如预期的那样继续改进,指导其在后续的推理中做出更好的选择。
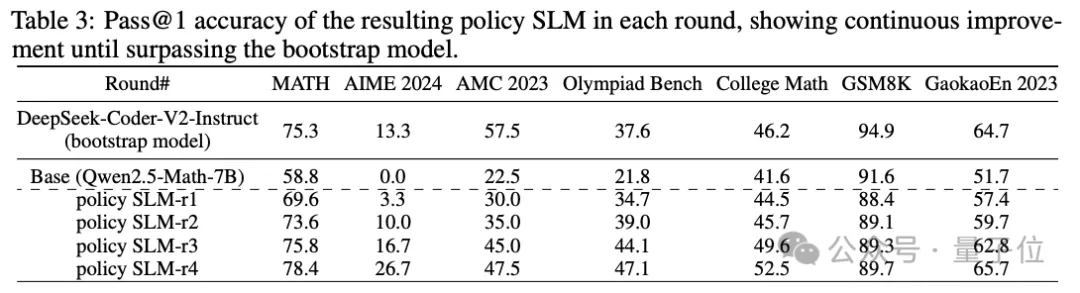
第三轮:
通过PPM增强的MCTS生成更高质量的数据,进一步提升模型的推理能力。
借助可靠的PPM-r2,研究人员在这一轮中执行PPM增强的MCTS以生成数据,从而获得更高质量的轨迹。此处涵盖训练集中的更多数学和奥林匹克级别问题(详细可见表2)。
然后,研究者使用生成的推理轨迹和自我注释的Q值,来训练新策略SLM-r3和PPM-r3——这两者都显示出显著的改进。
第四轮:
通过增加MCTS回滚次数,解决具有挑战性的数学难题。
前第三轮后,虽然rStar - Math已经让SLM在小学和MATH题目上提高成功率,但奥赛级别题目成绩还是只有62.16%。
为此,团队采用了一种简单的策略,即对于在16次MCTS部署后未解决的问题,会额外执行64次部署。
如果需要,这个次数可以增加到128次。
此外,研究者们还使用不同的随机种子进行多个MCTS扩展,最后将奥赛级别问题的成功率提高到80.58%。
△此处再贴一次表2,方便大家查阅
综上,经过四轮自我进化,747k数学题的成绩已经来到了90.25%。
剩下的未解决的问题中,很大一部分都是综合问题。
研究者人工手动审查了20个问题的随机样本,发现其中19个问题被错误地标记为错误答案。
基于此,团队得出结论:剩余的未解决的问题质量较低,因此自我进化的脚步终止在第4轮。
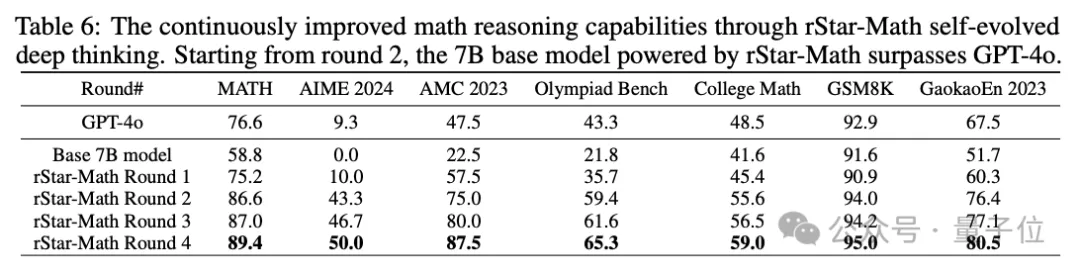
实验评估与发现
下面的表5,显示了rStar-Math与最先进的推理模型进行比较的结果。
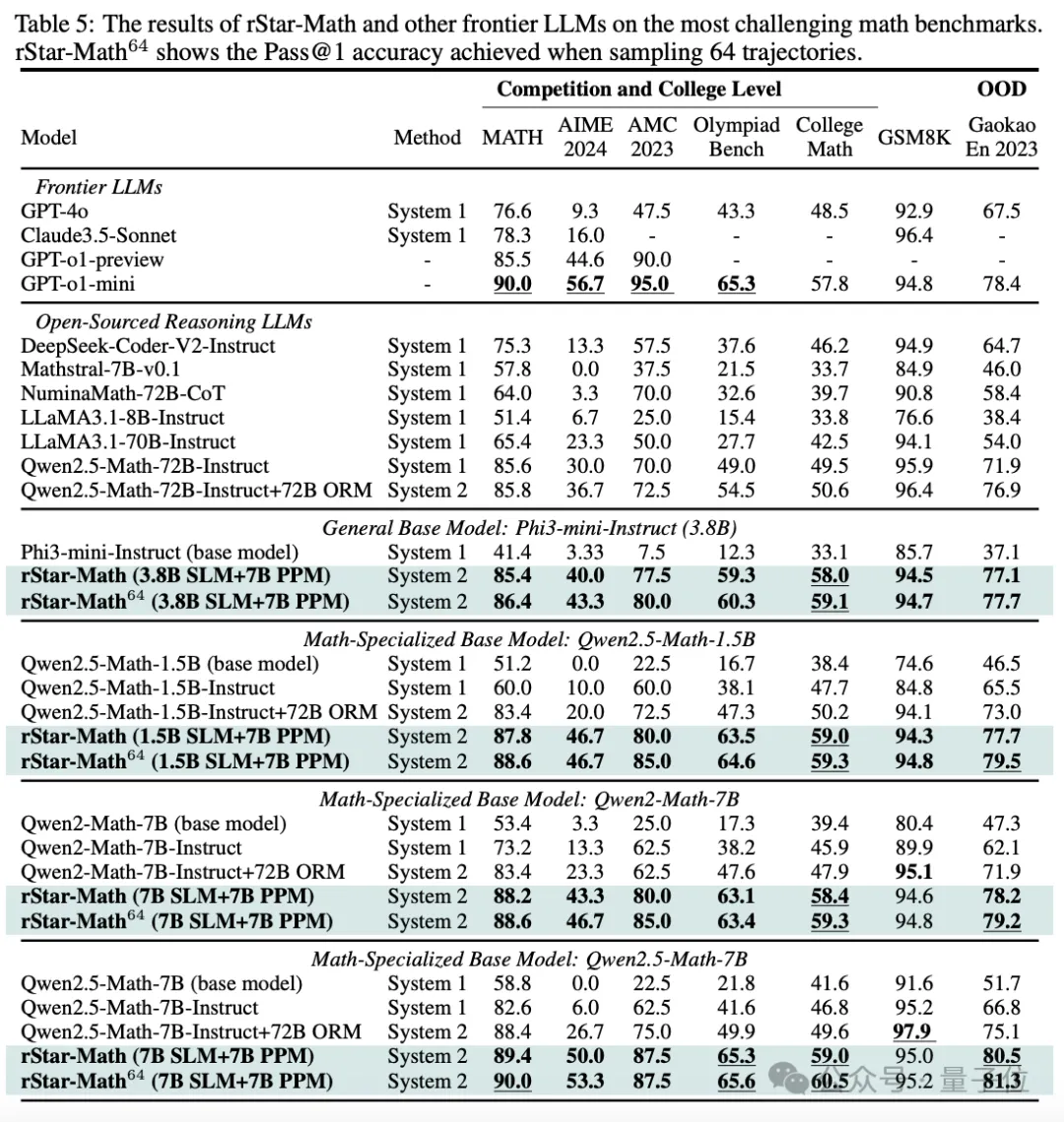
有三个值得说道说道的观察发现:
第一,rStar-Math 显著提高了SLM的数学推理能力,以小得多的模型尺寸,实现了与OpenAI o1相当,甚至超过o1的性能。
例如,Qwen2.5-Math-7B最初在MATH上的准确率为58.8%,使用rStar-Math后,准确率显著提高到90.0%,优于o1-preview和Claude 3.5 Sonnet,和o1-mini打了个平手。
在College Math基准测试中,rStar-Math后Qwen2.5-Math-7B的比o1-mini高出 2.7%。
在AIME 2024上,rStar-Math后的Qwen2.5-Math-7B得分为53.3%,不及o1-mini的56.7%。不过,7B模型在AIME I 和 II 中解决了8/15的问题,在最聪明的高中数学学生中排名前 20%。
而未解决的问题中,有8个是需要视觉里觉的几何图形题,这个功能目前rStar-Math还不支持。
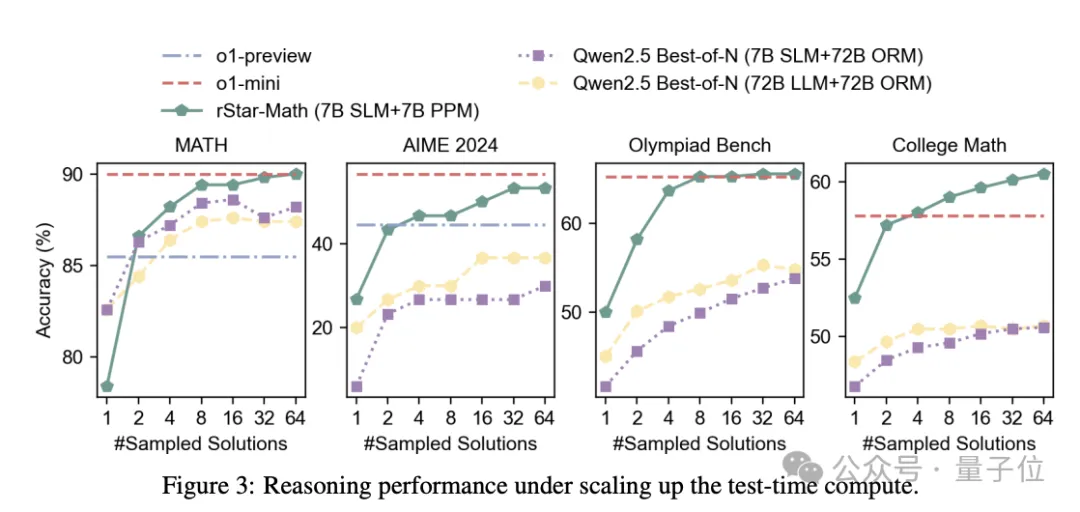
第二,尽管使用较小的政策模型(1.5B-7B)和奖励模型(7B),但rStar-Math的性能明显优于最先进的System 2基线。
与使用相同的基本模型(Qwen2-Math-7B、Qwen2.5-Math-1.5B/7B)但奖励模型 (Qwen2.5-Math-RM-72B) 大10倍以上的Qwen Best-of-N基线相比,rStar-Math始终将所有基本模型的推理准确性提高到最先进的水平。
即使与Qwen2.5-Math-72B-Instruct的策略模型大10倍以上的N-Best-of-N对比,使用相同数量的采样解决方案,rStar-Math也在除GSM8K之外的所有基准测试中也超过了它。
第三,除了MATH、GSM8K和AIME等可能存在过度优化的知名基准测试之外,rStar-Math在其它具有挑战性的数学基准测试中表现出很强的通用性。
包括但不限于奥赛基准、大学数学和中国高考数学考试 (Gaokao)。
而且需要强调的是,rStar-Math训练集主要来自公共数据集,并没有针对这些基准测试进行特定的优化。
总的来说,实验结果验证了自进化、逐步验证推理轨迹和PPM的有效性。
One More Thing
本研究的共同一作分别是MSRA的Xinyu Guan和Li Lyna Zhang。
Li Lyna Zhang是工作的项目leader,本博都毕业于中国科学技术大学,目前是MSRA系统与网络组的高级研究员。

另一位共同一作,Xinyu Guan,在完成这项工作的时候是MSRA的实习生,这位同学当时还在北大读书。
BTW,论文中另一位作者Youran Sun参与项目时也是MSRA实习生,这位同学则是清华er。
啊,年轻人的世界,又是实习生呢~
arXiv:https://arxiv.org/pdf/2501.04519
代码和数据详见GitHub:https://github.com/microsoft/rStar