在很多需要处理全排列的场景下,Heap’s Algorithm 以其简洁和高效的特点受到广泛关注。它通过最少的交换操作,就可以递归地生成给定序列的所有排列。本文将详细介绍这一算法的原理,给出 C# 实现,并展示一个简单的调度示例,让你快速上手并运用到实际项目中。
认识 Heap’s Algorithm
Heap’s Algorithm 最早由 B. R. Heap 提出,用于在 O(n!) 的时间复杂度内生成 n 个元素的所有排列。它通过一系列递归调用和交换操作,不断产生新的排列结果。算法的两个核心思想是:
- 最小交换:仅在需要生成新的排列时交换元素,最大程度减少不必要的操作。
- 递归生成:通过对子序列做递归处理,再配合交换操作,形成完整的排列。
算法原理简述
对一个含有 n 个元素的序列进行全排列时,可以分为以下几个步骤:
- 如果 n = 1,序列本身就是唯一排列,输出结果即可。
- 循环 n 次:
递归生成前 n-1 个元素的所有排列。
依据当前循环次数,决定交换对象(对于奇数次数,交换第 0 个元素与第 n-1 个元素;对于偶数次数,交换当前循环次数对应的元素与第 n-1 个元素)。
在多次迭代和交换后,会依次生成所有排列。
C# 实现示例
下面的代码展示了一个使用 Heap’s Algorithm 生成任意数组所有排列的示例。示例中,为了演示方便,我们使用了一个简单的 char 数组作为测试对象。
using System;
using System.Collections.Generic;
public class HeapsAlgorithmExample
{
public static void Main()
{
// 测试数组,可自由修改内容进行测试
char[] tasks = { 'A', 'B', 'C' };
// 存储所有排列结果
List<string> results = GeneratePermutations(tasks);
// 输出所有结果
Console.WriteLine("所有排列结果:");
foreach (var permutation in results)
{
Console.WriteLine(permutation);
}
}
/// <summary>
/// 生成指定数组所有排列并返回字符串形式
/// </summary>
/// <param name="array">需要排列的字符数组</param>
/// <returns>所有排列的列表</returns>
public static List<string> GeneratePermutations(char[] array)
{
List<string> permutations = new List<string>();
GeneratePermutations(array, array.Length, permutations);
return permutations;
}
/// <summary>
/// Heap's Algorithm 递归函数
/// </summary>
/// <param name="array">需要排列的字符数组</param>
/// <param name="size">当前处理中所使用的数字长度</param>
/// <param name="results">用来保存排列结果的列表</param>
private static void GeneratePermutations(char[] array, int size, List<string> results)
{
// 若当前处理长度为1,说明已经固定了前面所有元素
if (size == 1)
{
// 将当前数组转换为字符串加入结果
results.Add(new string(array));
return;
}
// 继续生成长度 size - 1 的所有排列
for (int i = 0; i < size; i++)
{
GeneratePermutations(array, size - 1, results);
// 根据当前层级是奇数还是偶数决定如何交换
if (size % 2 == 1)
{
// 奇数层,交换第0个元素和第 size-1 个元素
Swap(array, 0, size - 1);
}
else
{
// 偶数层,交换第 i 个元素和第 size-1 个元素
Swap(array, i, size - 1);
}
}
}
/// <summary>
/// 交换数组中两个元素
/// </summary>
private static void Swap(char[] array, int indexA, int indexB)
{
char temp = array[indexA];
array[indexA] = array[indexB];
array[indexB] = temp;
}
}运行输出示例
以输入 {'A', 'B', 'C'} 为例,可能的输出排列包括:
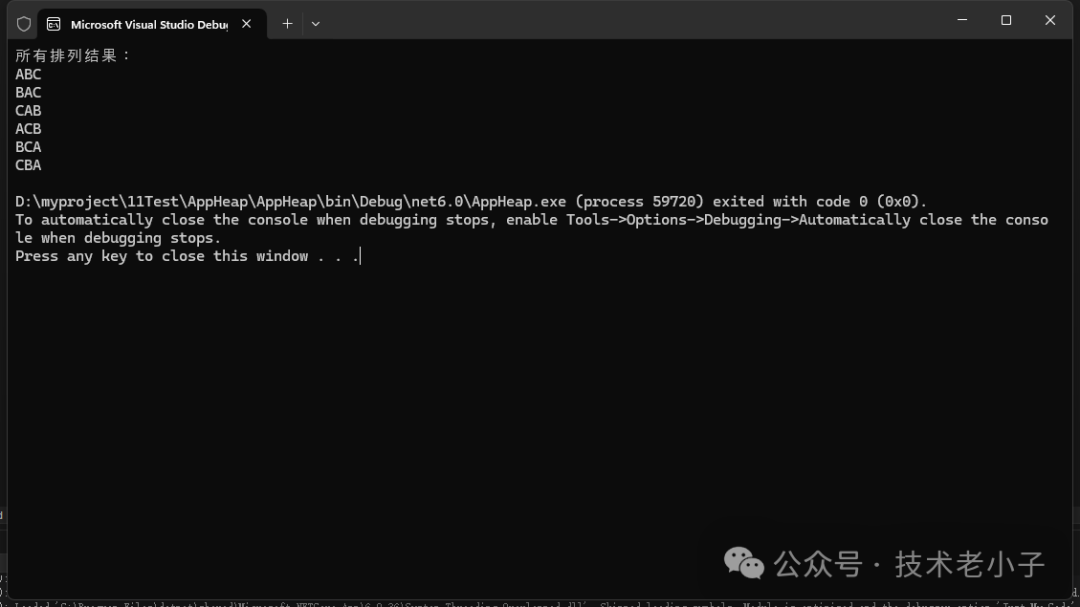 图片
图片
(不同的初始交换策略可能导致顺序稍有不同,但最终生成的排列集一致。)
Linq示例
namespace AppHeap
{
// 扩展方法:生成排列
public static class EnumerableExtensions
{
public static IEnumerable<IEnumerable<T>> Permutations<T>(this IEnumerable<T> source)
{
return source.Permutations(source.Count());
}
public static IEnumerable<IEnumerable<T>> Permutations<T>(this IEnumerable<T> source, int count)
{
if (count > source.Count())
throw new ArgumentException("Count cannot be greater than source size.");
return PermutationsImpl(source, count);
}
private static IEnumerable<IEnumerable<T>> PermutationsImpl<T>(IEnumerable<T> source, int count)
{
if (count == 0)
yield return Enumerable.Empty<T>();
else
{
int index = 0;
foreach (T element in source)
{
var remainingItems = source.Where((e, i) => i != index);
foreach (var permutation in PermutationsImpl(remainingItems, count - 1))
{
yield return permutation.Prepend(element);
}
index++;
}
}
}
}
internal class Program
{
public static void Main()
{
char[] tasks = { 'A', 'B', 'C' };
var uniqueCombinations = tasks
.Permutations()
.Select(p => new string(p.ToArray()));
foreach (var combination in uniqueCombinations)
{
Console.WriteLine(combination);
}
Console.WriteLine($"\n总组合数:{uniqueCombinations.Count()}");
}
}
}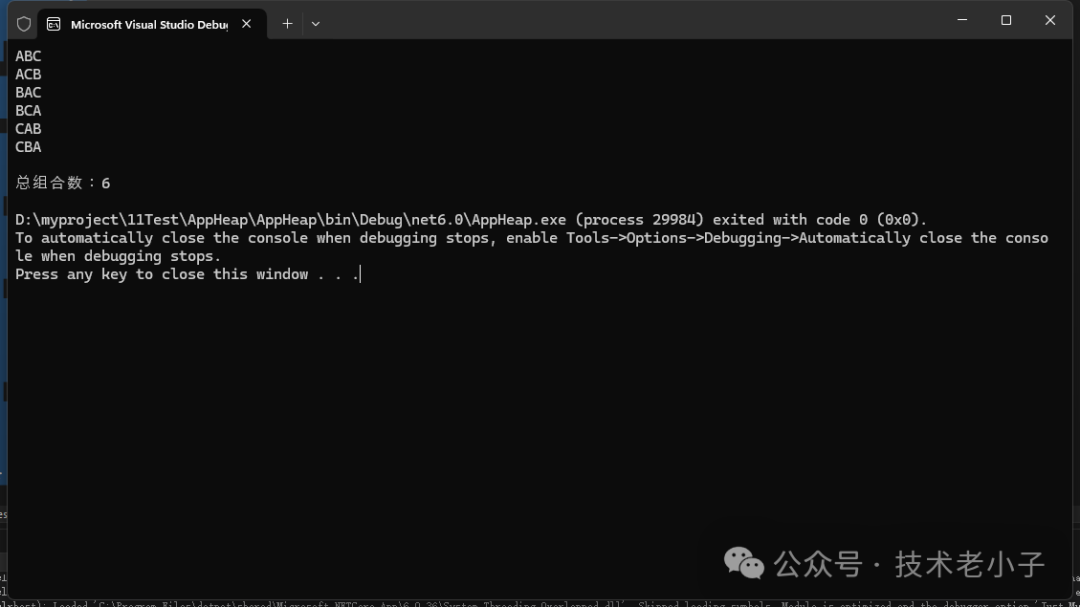 图片
图片
应用示例:简单调度问题
在实际场景中,常常需要考量任务的不同执行顺序。例如,有一组任务 {A, B, C},我们想知道所有可能的完成顺序,以帮助评估时间、资源或依赖关系。使用上述方法,我们就能将所有可能的执行顺序一并罗列出来,进而对每一种情况进行分析——例如,统计在不同顺序下完成任务的总耗时、判断是否有资源冲突等。
对于更复杂的调度需求,如任务间存在优先级或依赖关系,可以在生成排列后再进行过滤或排序,以排除不满足约束的情形,或根据自定义规则从所有排列中选取最优方案。
结语
Heap’s Algorithm 通过最少的交换次数,在 O(n!) 的时间内生成 n 个元素的所有排列,适用于各种需要遍历所有顺序的场景。无论是基础学习、学术研究,还是需要枚举方案的生产环境,这一算法都是简单且高效的工具。希望通过本文的示例,你能对 Heap’s Algorithm 的核心思想和 C# 实现方式有更加直观的认识,并能够根据自己的业务需求进行扩展和应用。