在现代制造业中,质量管理已成为提升竞争力的关键环节。 SPC(统计过程控制)控制图作为一种数据驱动的质量管理工具,能够帮助企业实时监控过程变化,快速识别异常,从而降低缺陷率,提升生产效率。
什么是控制图?
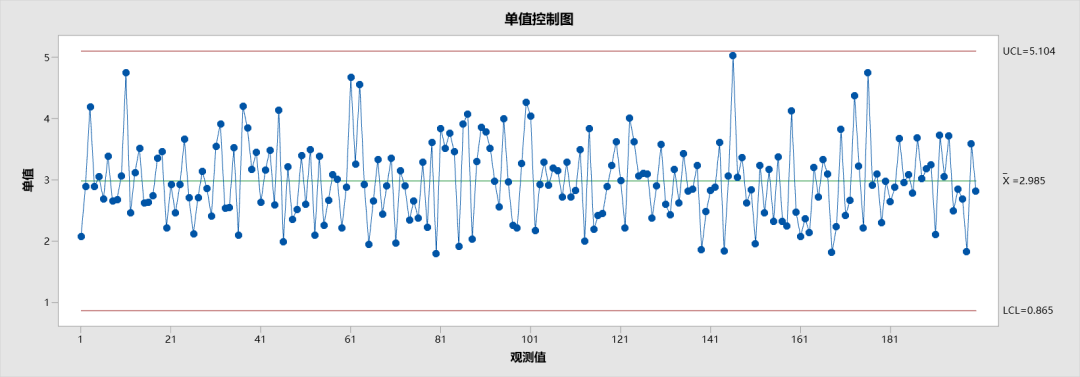
控制图是一种用来监测过程是否失控的工具,它能够帮助识别 特殊原因变异 的存在。当出现特殊原因变异时,表明过程不再稳定,必须采取纠正措施。
 图片
图片
控制图以时间顺序绘制过程数据的变化趋势。大多数控制图包含以下三个关键要素:中心线、上控制限 和 下控制限。
- 中心线 代表过程的均值。
- 控制限 表示过程的波动范围,通常设置为距离中心线上下各 3σ 的位置(即三倍标准差)。
如果数据点随机分布在控制限范围内,说明过程处于受控状态。但如果数据点落在控制限之外,或呈现非随机模式,则说明过程失控,存在 特殊原因变异,需要采取进一步的分析和调整措施。
控制图中的点
控制图中的每个数据点可以是单个观测值(如 I 图中的个体值),也可以是子组观测值的统计指标(即质量特征),如子组观测值的 均值 (Xbar)、移动极差 (MR)、标准差 (S)、极差 (R),或 Z 分数 (Z) 标准化后的值。这些统计指标的选择直接决定了控制图的类型。
- Xbar 控制图 (x̄):在子组中拥有连续数据的情况下监视过程的均值。
- S 控制图 (Standard Deviation,σ):在拥有连续数据且子组大小不小于 9 的情况下监视过程的变异(标准差,σ)。
- R 控制图 (Range):在拥有连续数据且子组大小不超过 8 的情况下监视过程的变异(极差)。
- I 控制图 (Individual):监控单个观测值或子组的均值,适用于逐点测量和样本量较少的场景。
- MR 控制图 (Moving Range):监控连续观测值之间或子组均值之间的移动极差。
- 区域控制图 (Zone):监视过程的均值,该控制图使用西格玛区间(区域)和累积评分系统(而非特殊原因检验)来检测失控点。您可以标绘子组或单个观测值中的数据。
- Z-MR 控制图 (Z-Moving Range):监控标准化后的观测值及其移动极差,结合 Z 图和 MR 图的特点。
控制图中的中心线
在控制图中,中心线 代表的是实际过程中的质量特征均值,而不一定是期望的过程(即规格测量值)均值。中心线是控制图上的水平参考线,表示所绘制质量特征的平均值。通过观察中心线,可以评估过程相对于该平均值的表现。当过程处于受控状态时,数据点会围绕中心线随机波动。
根据质量特征和分析的颗粒度,控制图可以分为不同类型。若分析颗粒度为子组,常见的控制图包括 Xbar 控制图、S 控制图、R 控制图、I 控制图、MR 控制图 和 区域控制图;若分析颗粒度为个体,则常使用 Z-MR 控制图、MR 控制图 和 I 控制图。
不同类型的控制图适用于不同的数据特征和监控需求。例如,对于单个测量值,我们可能选择 I-MR 控制图;对于小样本子组的测量数据,则可以使用 X-bar 和 R 控制图。而当需要监控较大样本或复杂过程时,X-bar 和 S 控制图 更为合适。
控制图中的控制限
控制图中的 控制限 代表了过程的变异范围,并帮助判断过程是否失控。控制限是位于中心线上下的水平线,用于判断过程是否超出控制范围。上控制限和下控制限基于过程中的随机变异。默认情况下将控制限设置为距离中心线 3 个标准差的位置,即上下各 3σ;如有指定检验规则,根据规则"1个点距离中心线大于K个标准差"条件指定上下控制限。
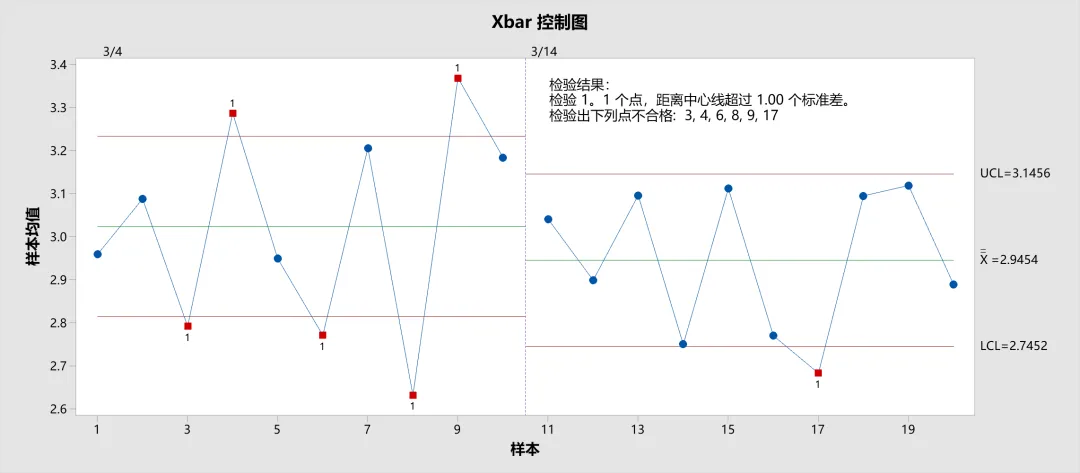
例如,下面 Xbar 图 的检验规则为大于1个标准差的点就为异常点,它的上下控制限就为上下各1个σ。
 图片
图片
需要注意的是,控制限 与 规格限 是不同的。控制限基于过程变异,而规格限则是根据客户要求设定的。一个过程可能处于受控状态,但仍然无法满足规格要求。
常见原因变异和特殊原因变异
正常情况下,任何过程中都会出现一定程度的变异。常见原因变异是过程中正常的或预期的变异。特殊原因变异是因异常情况导致的意外变异。一定要确定并尝试消除特殊原因变异。控制图上的失控点和非随机模式指示是否存在特殊原因变异。例如下图中的特殊原因变异示例:
 图片
图片
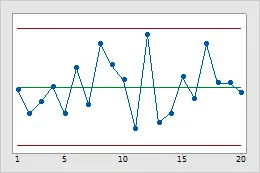
如果过程不包含任何特殊原因变异,只存在常见原因变异,则过程是稳定的。控制图和运行图为过程稳定性或不稳定性提供了很好的说明。评估其能力或启动改进之前,过程必须的稳定的。
 图片
图片
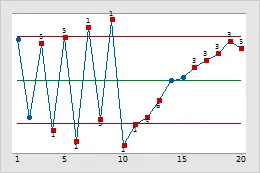
由于数据表现为随机分布并且未违反 8 个控制图检验中的任何一个,因此此过程是稳定的。
 图片
图片
控制图中的特殊原因检验
为了更高效地识别这些特殊原因(Special Cause Variation),控制图通常提供多种检验规则,通过分析数据点的分布、趋势和变化模式,判断过程是否存在异常情况。这些规则可以灵活调整以适应不同的行业标准和需求。以下是几种常见的特殊原因检验方法:
- 单点超出控制限:检验单个点是否超出控制限,用于识别显著的异常情况。这是最基础且普遍使用的检验规则,可以快速发现过程失控的情况。
- 连续 K 点落在中心线同一侧:检验数据点是否偏离中心线并形成一致的偏移模式。这种情况通常指示过程均值或变异发生了小幅但持续的变化。
- 连续 K 点呈递增或递减趋势:检测数据是否存在显著的趋势。这种检验能够识别由系统性原因引起的逐步变化。
- 连续 K 点交替上升和下降:检测数据是否显示系统性波动。这可能表明过程中的某些影响因子以周期性模式干扰了系统。
- K 个点中有 K+1 个点超过 2 倍标准差(同侧):检测过程的小幅偏移,适合对过程波动较敏感的场景。
- K 个点中有 K+1 个点超过 1 倍标准差(同侧):同样用于检测小幅偏移,但对过程变异的要求更低,适合更细微的变化。
- 连续 K 点落在中心线附近(±1 倍标准差范围内):检测过于集中的数据分布,这可能表明控制限设置过宽,或子组数据存在系统性分层现象。
- 连续 K 点分布在远离中心线的区域(超过 1 倍标准差范围):检测混合模式,其中数据点倾向于远离中心线,更靠近控制限。这通常表明过程受多个系统性因素的共同影响。
通过结合这些检验规则,用户可以从不同角度监控过程的动态变化,不仅能快速发现问题,还能帮助定位潜在的根因。这种方法适用于制造业、服务业等对质量要求较高的场景,是实现精细化质量管理的重要工具。
子组变量:Xbar控制图
在统计学中,“bar” 是表示数学符号 “上横线” 的术语,而 “x̄” 代表平均数。因此,Xbar 控制图指以子组的平均数为监测目标的控制图,主要适用于子组数据为连续型变量的场景。通过监测过程均值的稳定性,Xbar 控制图能够有效帮助识别并纠正过程中的不稳定因素,确保生产过程的质量一致性。
Xbar 控制图中的点以子组的均值为纵轴 (Y 轴) 值,横轴 (X 轴) 则表示子组的序号,点的总数即为子组的数量。
控制图的中心线代表所有子组均值的总体均值,因此数学符号上通常表示为双横线 “X̿”。
控制限则是基于子组均值计算得出的,通常设置为距离中心线上下各 3 倍标准差的范围,用以判断过程是否超出可接受的随机波动范围。
下面控制图示例都是基于网上销售图书的公司订单和到达时间的数据示例,200条20天的数据(每天10条)。
- 日期:订单的交货日期
- 天数:订单的到达日期和下单日期之间的差值
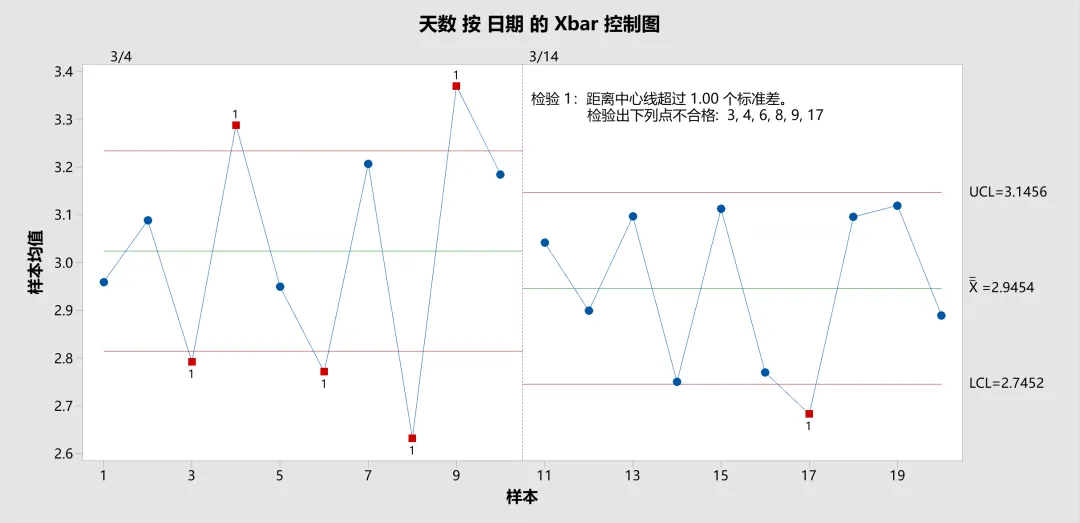
这是一张基于示例数据绘制的 Xbar 控制图,用于监测订单交付天数的过程均值稳定性。图中包含以下信息:
- 数据点:每个点表示某一天订单天数的子组均值。
- 中心线 (X̿):代表所有子组均值的平均值,反映过程的整体中心。
- 控制限 (UCL 和 LCL):显示子组均值在 ±1 倍标准差范围内的波动(为演示修改规则1的 K 值为 1)。
- 阶段划分:以 3/14 为界划分为两个阶段,可以明显看出 3/14 之后订单交付效率和稳定性有所上升。
- 标准差算法为合并标准差(Pooled Standard Deviation)并使用C4无偏常量纠偏。
通过该图表,能够直观发现订单交付过程的潜在波动,为进一步分析提供依据。
 图片
图片
子组变量:R控制图
R在这里是极差 (Range) 的首字母,R 控制图因此以子组的极差为监测目标,主要适用于子组数据为连续型变量的场景。通过监测过程波动范围的稳定性,R 控制图能够有效帮助识别并纠正过程中的异常波动因素,确保生产过程的质量一致性。
R 控制图中的点以子组的极差为纵轴 (Y 轴) 值,横轴 (X 轴) 则表示子组的序号,点的总数即为子组的数量。
控制图的中心线代表所有子组极差的总体均值。控制限则是基于子组极差的标准差,通常设置为距离中心线上下各 3 倍标准误差的范围,用以判断过程是否超出可接受的随机波动范围。
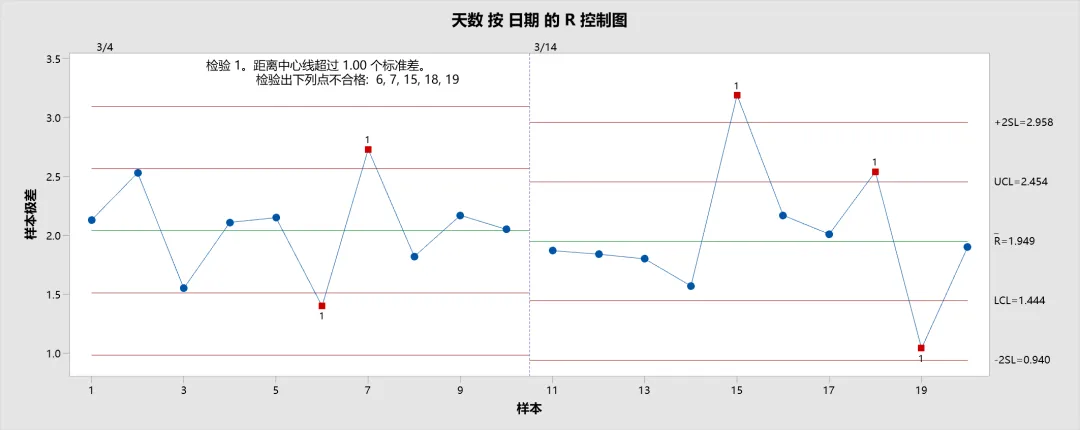
这是一张基于示例数据绘制的 R 控制图,用于监测订单交付天数的过程波动范围稳定性。图中包含以下信息:
- 数据点:每个点表示某一天订单天数的子组极差,即子组最大值与最小值之差。
- 中心线 (R̅):代表所有子组极差的平均值,反映过程的整体波动范围。
- 控制限 (UCL 和 LCL):显示子组极差在 ±1倍标准误差范围内的波动(为演示修改规则1的 K 值为 1)。
- 阶段划分:以 3/14 为界划分为两个阶段,可以明显看出 3/14 之后订单交付的极差波动范围有所增加。
- 标准差算法为合并标准差(Pooled Standard Deviation)并使用C4无偏常量纠偏
 图片
图片
通过该图表,可以清晰地识别订单交付过程中波动范围的潜在异常,为进一步优化过程和改进质量管理提供支持。
子组变量:S控制图
S 是标准差(Standard Deviation)首字母,S 控制图因此以子组的标准差为监测目标。
S 控制图中的点以子组的标准差为纵轴 (Y 轴) 值,横轴 (X 轴) 则表示子组的序号,点的总数即为子组的数量。
控制图的中心线代表所有子组标准差的均值。控制限则基于子组标准差的分布特性推导,通常设置为距离中心线上下各 3 倍标准误差的范围,用以判断过程是否超出可接受的随机波动范围。
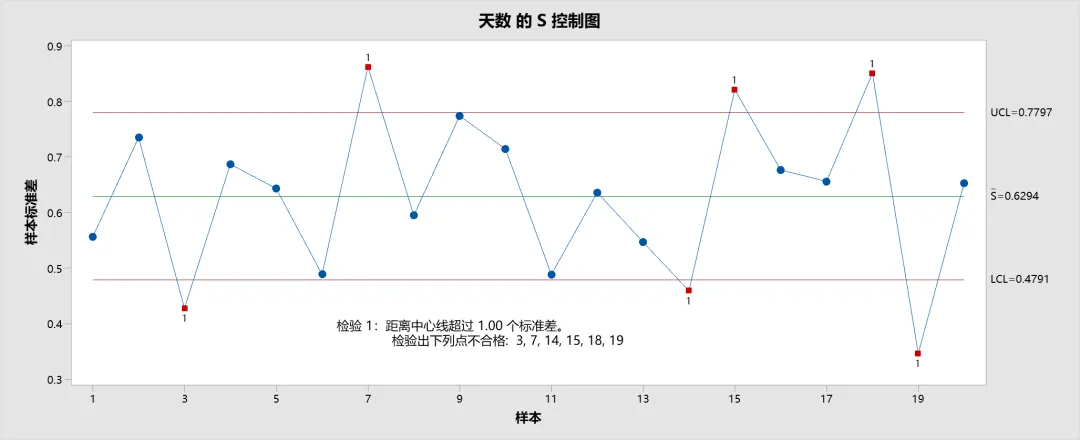
这是一张基于示例数据绘制的 S 控制图,用于监测订单交付天数的过程波动稳定性。图中包含以下信息:
- 数据点:每个点表示某一天订单天数的子组标准差。
- 中心线 (S̅):代表所有子组标准差的总体均值,反映过程的整体波动水平。
- 控制限 (UCL 和 LCL):显示子组标准差在 ±1倍标准误差(σ)范围内的波动(为演示修改规则1的 K 值为 1)。
- 标准差计算:采用合并标准差 (Pooled Standard Deviation) 并使用 C4 无偏常量进行修正。
 图片
图片
子组变量:I控制图
I 是个体(Individual)首单词,子组的I控制图即子组均值单值控制图。I 控制图用于监控子组的均值波动,特别适用于数据较为稳定的过程或需要观察整体过程水平变化的情况。
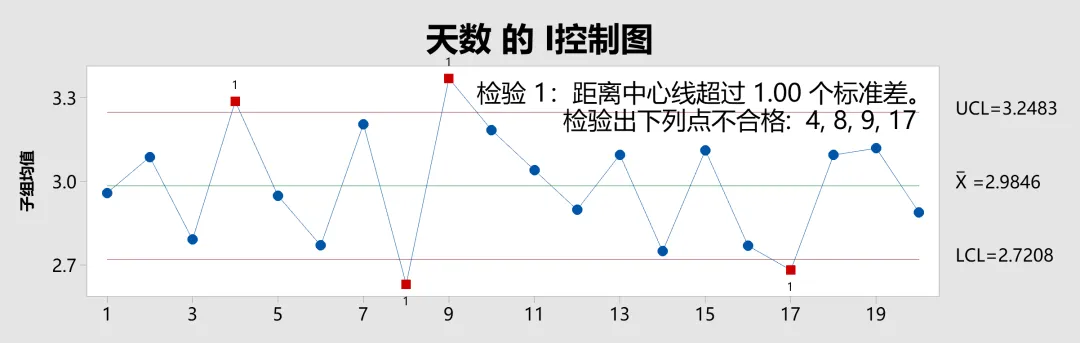
假设我们要监测生产过程中每一天订单交付天数的均值波动。使用 I 控制图时,关注的关键数据点如下:
- 数据点:每个点代表一个子组(例如某一天)订单交付天数的均值。
- 中心线 (X̅):总体平均值,显示整个过程的稳定性。
- 控制限 (UCL 和 LCL):设定控制限为 ±1倍标准误(组间标准差)差范围内的波动(为演示修改规则1的 K 值为 1)。
- 标准差计算:采用合并标准差 (Pooled Standard Deviation) 并使用 C4 无偏常量进行修正。
 图片
图片
子组变量:MR控制图
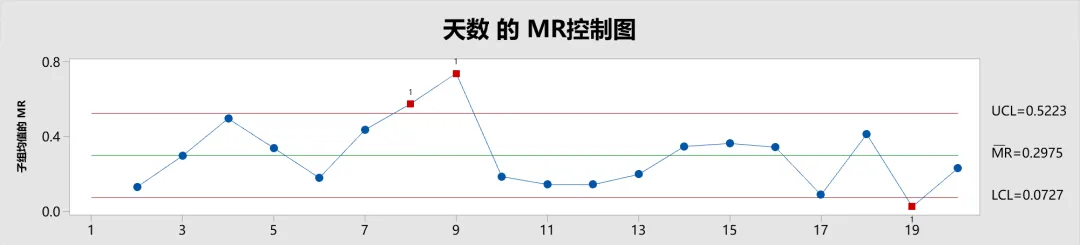
I 是个体(Moving Range)首单词,子组MR控制图即子组均值的MR控制图。子组MR控制图用于监控相邻子组均值的波动
假设我们要监测生产过程中子组MR控制图:
- 数据点:每个点表示相邻两个子组(子组内的均值)(例如相邻两天)之间的绝对差异。纵轴(Y 轴)为这些差异,横轴(X 轴)为子组的序号,点的总数即为子组的数量。
- 中心线 (MR̅):该线代表所有相邻数据点差异的平均值,反映过程的整体波动水平。
- 控制限 (UCL 和 LCL):设定控制限为 ±1倍标准误(组间标准差)差范围内的波动(为演示修改规则1的 K 值为 1)。
- 标准差计算:采用合并标准差 (Pooled Standard Deviation) 并使用 C4 无偏常量进行修正。
 图片
图片
子组变量:区域控制图
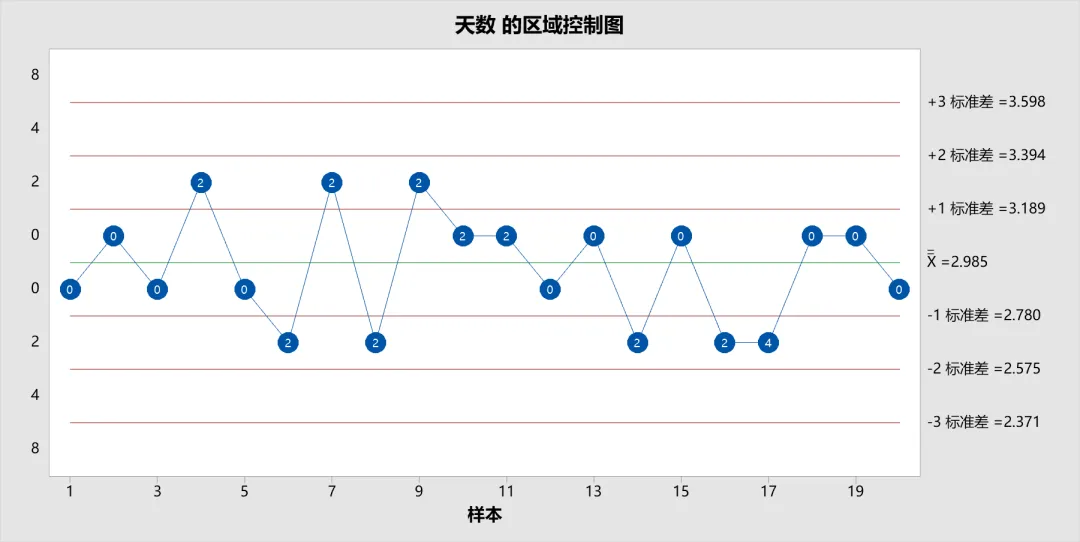
区域控制图(Zone Chart)是一种用于监控过程均值的控制图,它采用了基于标准差区间(即“区域”)的方式,并使用累积评分系统来代替传统的特殊原因测试,用以检测过程是否失控。通过这种方法,控制图能够在发现异常波动时及时响应,而不需要通过复杂的测试规则。
区域控制图中点和中心线与xbar 是一样的,差别是没有上下控制线,而是用标准差区间区间代替,特殊原因检验用累积评分系统代替,当达到8分表明这个点不可控。为在中心线一侧的连续点添加了用来计算累积分值的区域分值,并为每个点标记了累积分值。
记分的权重规则一般如下:
- 区间1:中心线 1个标准差以内,记0分
- 区间2:1个与 2 个标准差之间,记2分
- 区间3:2个与3个标准差之间,记4分
- 区间4:大于 3 个标准差,记8分
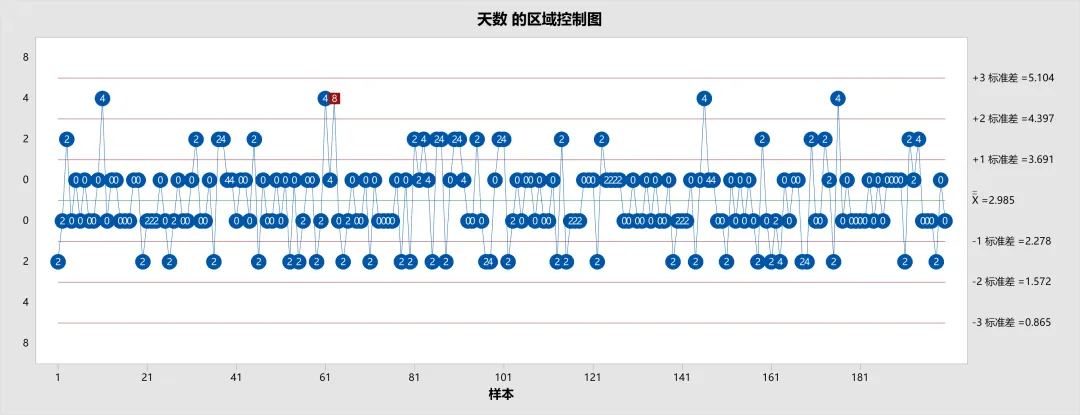
区域图可以子组间、也可以为个体的单值控制图,如下图:
 图片
图片
 图片
图片
单值:I 控制图
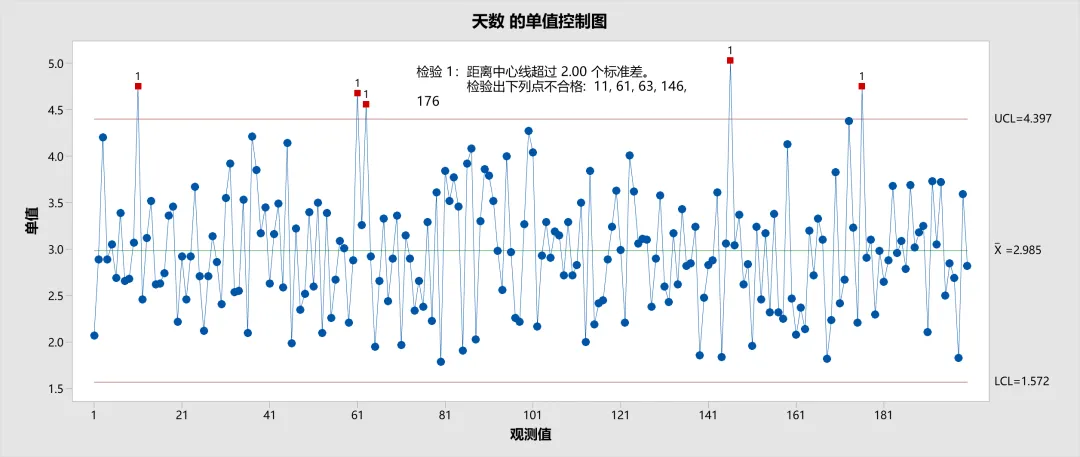
单值控制图(I 控制图)是一种不依赖子组的控制图,适用于监控个别数据点的波动趋势。与传统的子组控制图相比,单值控制图更加直观,易于理解,尤其适用于样本量较小或没有自然分组的过程。
- 单值 I 控制图的点:每个数据点代表一个单独的观测值(例如每一天的生产数据)。这些数据点直接反映过程中的单次波动情况,帮助识别是否有异常的波动出现。
- 单值 I 控制图的中心线:中心线(X̅)代表过程数据的总体均值,显示了整个过程的稳定性水平。所有的点会围绕中心线波动,通过观察数据点与中心线的关系,可以判断过程是否维持在预期的稳定范围内。
- 单值 I 控制图的控制限(UCL、LCL):控制限是基于数据分布特性计算得出的,通常设定为中心线的上下3倍标准误差(3σ)。控制限分为上控制限(UCL)和下控制限(LCL),它们定义了过程波动的可接受范围。如果数据点超出了这个范围,说明过程可能出现异常,需要进行干预和调整。
- 标准差的估算方法一般为:移动极差平均值、移动极差中位数、递差均方和平方根
 图片
图片
单值:MR 控制图
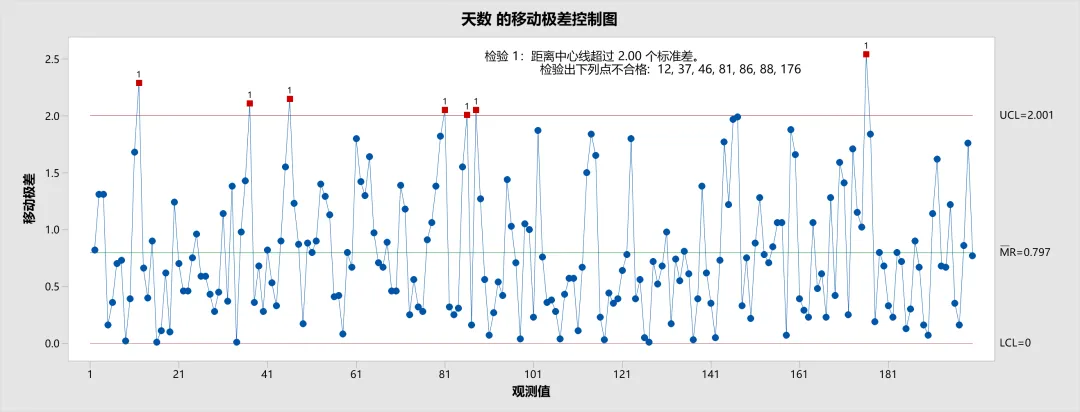
单值 MR 控制图(Moving Range)是一种用于监控相邻数据点间波动的控制图,常与单值 I 控制图配合使用。MR 控制图可以帮助识别过程波动的异常来源,特别是相邻点之间的突变情况。
- MR 控制图的点:每个数据点表示相邻观测值之间的绝对差值(移动极差),直接反映过程中的局部波动幅度。
- MR 控制图的中心线:中心线(MR̅)代表所有移动极差的平均值,显示了过程局部波动的总体水平。
- MR 控制图的控制限(UCL、LCL):上控制限(UCL)通常设定为中心线的 3.268 倍,基于统计经验值,无下控制限(LCL)。超出控制限的点表明过程可能存在异常波动。
- 标准差的估算方法一般为:通常采用移动极差平均值 、或移动极差中位数
MR 控制图通过分析局部变化趋势,能够有效辅助判断过程的短期波动是否处于可控范围内。
 图片
图片
单值: Z-MR 控制图
Z-MR 控制图适用于短期生产过程中监控不同部件或产品的均值和变异情况,特别是在每次生产的单位数量较少时。
短期生产往往缺乏足够的数据来准确估计过程参数。例如,一台机器可能在一次生产中仅制造 20 个零件,然后调整设置以生产不同的零件或产品。即使每次生产的数量足够多,也需要为每种零件单独绘制控制图,因为不同零件的均值和标准差可能不同。短期控制图通过合并和标准化数据,为这些问题提供了解决方案。
Z-MR 控制图的特点:
- 假设每个部件或批次都有独特的均值和标准差。
- 通过将观测值减去均值,并除以标准差,对数据进行标准化。
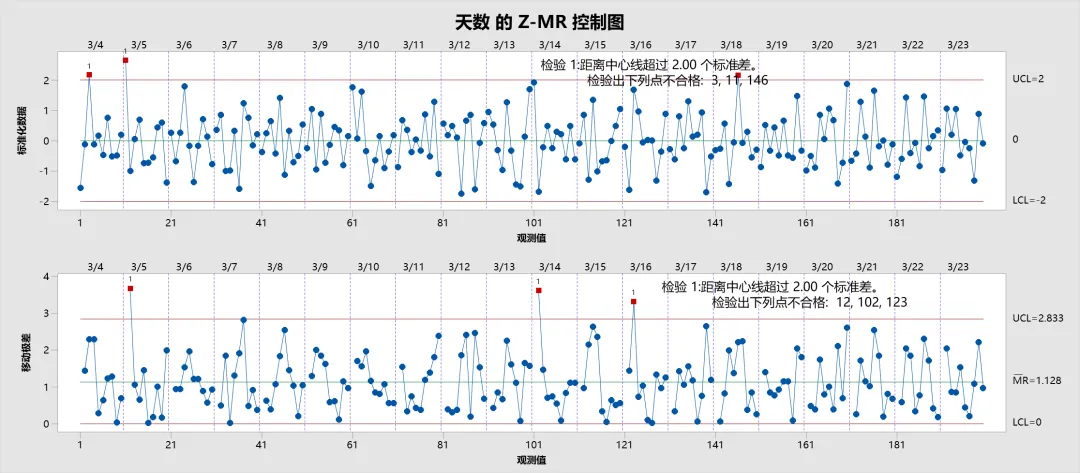
- 图中绘制标准化后的个体观测值 (Z 值) 和移动极差 (MR),从而在同一控制图上评估不同生产批次的数据。
Z-MR 控制图能够将短期运行中的多样化产品数据整合为统一的标准化视图,使您在单一图表中有效监控多个批次或产品的过程均值和波动情况。
 图片
图片
控制图是统计过程控制(SPC)的核心工具,用于监控质量过程的稳定性,快速识别异常和特殊原因变异。通过中心线、控制限和多种检验规则,控制图帮助判断过程是否超出正常波动范围。不同类型的控制图(如Xbar、R、S图等)适用于不同场景,为制造业等领域的精细化质量管理提供数据支撑,提升生产效率和质量一致性。










































