近期,OpenAI 号称最强推理模型的推出,引发了社区的热议,无论是性能还是价格,都产生了不少话题。最近,我们对 o1 新发布的 o1 满血版、o1 pro mode 模型进行了高难度数学测试,旨在深入探究其在数学推理方面的能力表现。同时以上海人工智能实验室的 InternThinker-Alpha、DeepSeek 的 DeepSeek-R1-Lite、月之暗面 k0-math 、阿里巴巴 QwQ-32B-Preview 等模型作为对比,「o1 pro」是否真的「自缘身在最高层?」
AGI-Eval 最新的高难度数学评测集 Math Pro Bench,试题来源包括全国高中数学联合竞赛、美国数学邀请赛、全国硕士研究生招生考试等。从题型分布上看,各模型考研数学题正确率高于高中数学竞赛题 10%,提示考研数学题目难度相对简单。这一现象表明考研数学题目相对高中数学竞赛题而言,在知识运用的综合性与逻辑性方面可能更符合模型的训练模式与擅长领域。例如,在高中数学竞赛题中,可能涉及更多独特的解题技巧、创新性的思维方式以及对数学概念的深度挖掘,而模型在处理这些复杂且灵活的问题时可能面临更大的挑战。
话不多说,直接上评测结果 ——
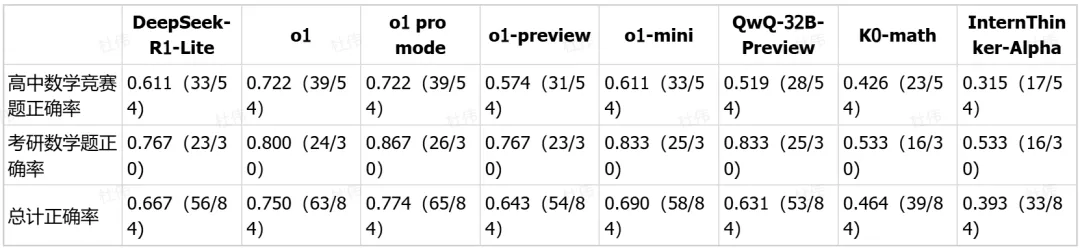
整体来看,o1 pro mode 在总计正确率上以 0.774(65/84)占据榜首,o1 以 0.750(63/84)紧随其后。这表明 o1 系模型在整体数学推理能力上具有较高的水平,能够较为有效地应对高难度数学问题。DeepSeek-R1-Lite 的总计正确率为 0.667(56/84),o1 - preview 的总计正确率为 0.643(54/84),其他模型的总计正确率相对较低,反映出它们在数学推理的全面性和准确性方面仍有提升空间。
其中在高中数学竞赛题方面,o1 pro mode 和 o1 均以 0.722(39/54)的正确率位居前列,展现出了较强的数学思维能力与解题技巧应用能力。DeepSeek - R1 - Lite 的正确率为 0.611(33/54),o1 - preview 的正确率为 0.574(31/54),其他模型如 QwQ - 32B - Preview、K0 - math、InternThinker - Alpha 的正确率则相对较低,分别为 0.519(28/54)、0.426(23/54)、0.315(17/54)。
在考研数学题上,o1 pro mode 以 0.867(26/30)的正确率脱颖而出,o1 的正确率为 0.800(24/30),QwQ-32B- Preview 和 o1- preview 的正确率均为 0.833(25/30)。DeepSeek - R1 - Lite 的考研数学题正确率为 0.767(23/30),而 K0 - math 和 InternThinker - Alpha 的正确率仅为 0.533(16/30)。
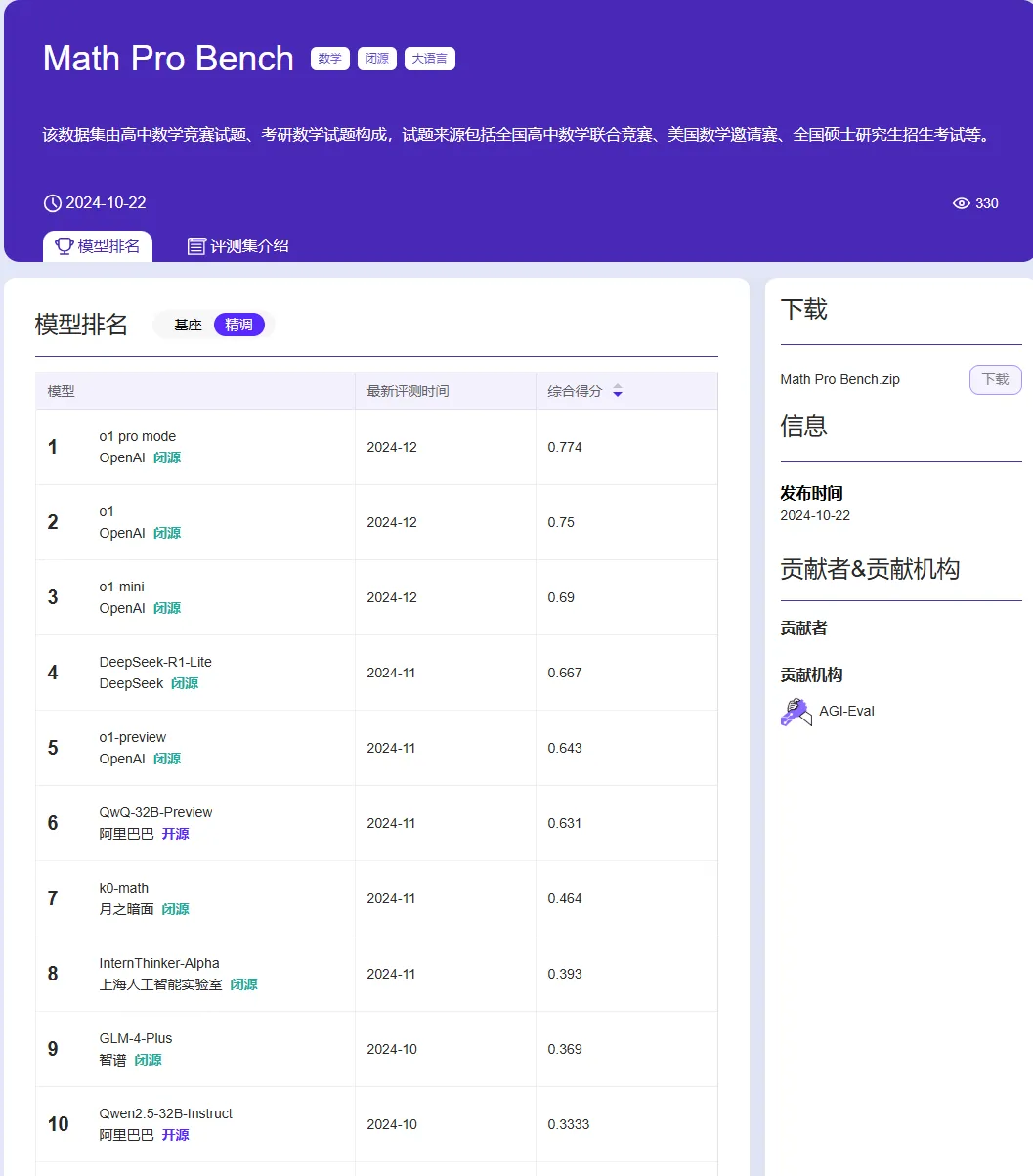
榜单链接:https://agi-eval.cn/evaluation/Math%20Pro%20Bench
除了推出评测榜单以外,AGI-Eval 也从模型的推理过程中,发现了一些有意思的现象和结论。
o1 pro 系列推理更快,思考更灵活
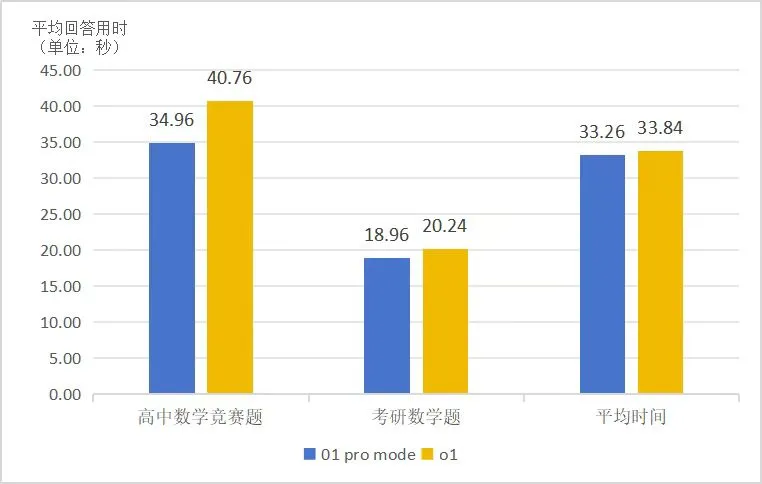
1. o1、o1 pro 总推理时间更短。在推理时间方面,o1 系模型展现出了显著的优势。o1 的总平均推理时间仅为 33.84s,o1 pro mode 更是缩短至 33.26s,而其他模型如 DeepSeek - R1 - Lite 等平均推理时间在 2min 以上。这一巨大的时间差距表明 o1 系模型在数学推理效率上远超其他同类模型,能够在更短的时间内完成复杂数学问题的推理与解答,这对于实际应用场景中对实时性要求较高的任务具有比较重要的意义。
prompt
Alice 和 Bob 玩以下游戏。面前有 n 个令牌堆放着。玩家轮流行动,Alice 先行动。在每一回合中,玩家从令牌堆中移除 1 个或 4 个令牌。移除最后一个令牌的玩家获胜。求小于或等于 2024 的正整数 n 的个数,使得 Bob 无论 Alice 如何行动都能保证他获胜。
o1 pro mode(用时 18 秒):
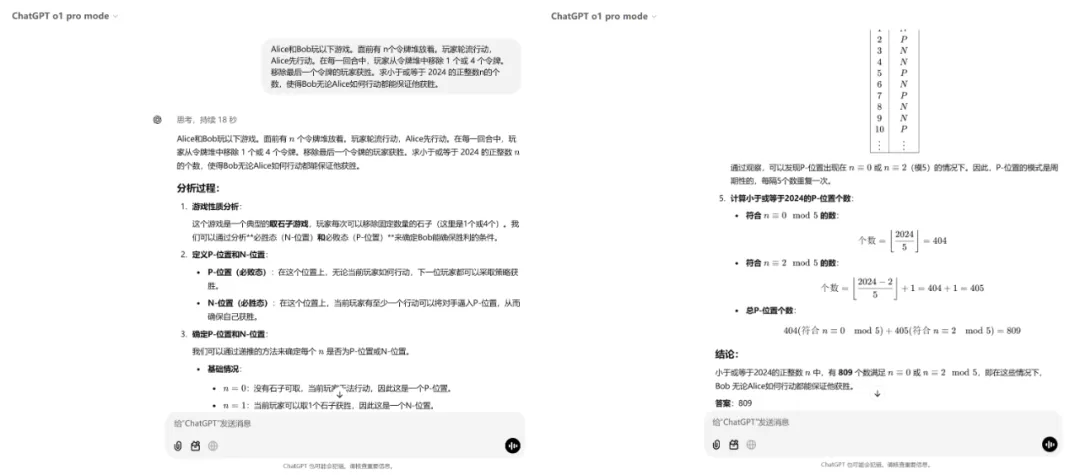
o1 (用时 26 秒):

2. o1、o1 pro 会根据题目难度调整推理时间。o1/o1 pro 的竞赛题平均推理时间为 34-40s,而考研题平均推理时间为 18-20s,约是前者的约一半。
3. o1 pro 模型能答对其他模型暂无法答对的题。在测试过程中,存在一些题目,如 :
“设 p 是最小的满足存在正整数 n 使得 n^4 + 1 可以被 2 整除的素数。求最小的正整数 m,使得 m^4 + 1 可以被 p^2 整除。”
这一题目仅有 o1 pro mode 答对,o1、Deepseek-R1-Lite 等其他模型均答错。这表明 o1 pro mode 在处理某些具有特殊数学结构和逻辑要求的题目时,具备独特的推理能力和解题思路,能够深入挖掘题目背后的数学原理与规律,从而找到正确的答案。而其他模型在面对这类复杂且具有挑战性的题目时,可能由于推理机制的局限性或知识储备的不足,无法准确地把握解题的关键要点,导致最终回答错误。
方法论与创新性
o1-pro 在处理数学问题时表现出更强的创新性和灵活性,能够结合多种数学理论和方法来解决问题,优于其他通用 AI 模型。o1 同样具有归纳与创新的能力,但与前者相比不够简洁直接,其他模型在这方面的能力则稍显不足。
prompt:
一只青蛙在正方形 A B C D 的四个顶点间跳跃,每次跳跃总是等可能地跳至与当前所在顶点相邻的两个顶点之一,且各次跳跃是独立的。若青蛙第一次跳跃前位于顶点 A ,则它第 6 次跳跃后恰好仍位于顶点 A 的概率为
o1 pro mode(用时 12 秒):
直接利用了正方形的对称性和跳跃的性质,避免了复杂的矩阵运算和特征值分析,更直观容易理解,适合初学者。

o1(用时 17 秒):
它的回答虽然正确,但涉及了状态转移矩阵和特征值分析,计算过程相对复杂,且需要一定的线性代数和概率论知识,对初学者来说可能不太友好。

Deepseek-R1-Lite(用时 1min):
和 o1 同样涉及了状态转移矩阵和特征值分析,但求解过程冗长复杂得多,阅读理解起来相对困难。

长链路推理与细节处理
在涉及大量计算的长链路推理中,一个小小的计算失误会模型思维链失败,使模型陷入死循环状态。o1 pro mode 和 o1 实现了对细节的精确控制,在进行长链路推理时能够尽量保持高度的准确性和稳定性。
prompt
实对称矩阵 A=\left (\begin {array}{ccc} 4 & -2 & 0 \\ -2 & 3 & -2 \\ 0 & -2 & 2\end {array}\right) 可通过正交相似变换化为对角阵__
o1 pro(用时 12 秒):
特征值与特征向量的求解涉及大量复杂的计算,每一步计算都是正确的,最后导向正确的结果

o1(用时 19 秒):
虽然得到了正确的答案,但过程不完全正确,例如第二步特征向量求解错误

Deepseek-R1-Lite:
在第一步计算特征值的过程中,就出现了计算错误,得到的特征多项式不正确,导致了后续求解特征方程的过程基于错误的多项式,从而无法找到正确的特征值。
此外,能看出推理模型也有明显的能力缺陷部分。如 Deepseek-R1-Lite 推理部分会存在中英夹杂或渲染不全的情况
人机协作评测新模式探索及高质量评测社区建设
鉴于传统评测方式难以充分反映模型的真实水平,AGI-Eval 创新性地提出了人机协作评测模式。在这种模式下,参与者可以与最新的大模型共同完成任务,既有助于提高任务完成度又便于建立更加直观的区分度。基于前期的一些用户实验表明,通过这种方式不仅可以获得更为简洁、完善的推理过程描述,还可以进一步提升用户与大模型之间的互动体验。未来,随着更多类似平台的出现和发展,相信人机协作将成为评测领域的一个重要发展方向。
人机社区链接:https://agi-eval.cn/llmArena/home
AGI-Eval 平台基于真实数据回流、能力项拆解等方式,自建万量级私有数据,并经过多次质检保证准确率。黑盒 100% 私有化数据,可保证评测数据不可 “穿越”。从数据建设到模型评测,实现全层级能力项目,一级能力涵盖指令遵循、交互能力、认知能力(含推理、知识、其他认知能力等);完美实现自动与人工评测相结合。
对于 Chat 模型,平台官方榜单结合主观、客观评测结果,中英文权重分布均衡。客观评测基于模型打分,可处理具有一定自由度问题,准确率 95%+;主观评测基于三人独立标注,并记录细分维度标签结果,全面诊断模型问题。

总结 1:推理模型优势探讨
(一)高效的推理算法
o1 系模型之所以能够在高难度数学测试中取得优异成绩,其高效的推理算法功不可没。通过对推理过程的优化与加速,模型能够在短时间内对复杂的数学问题进行深入分析与推理,快速找到解题的思路与方法。这种高效的推理算法可能基于先进的神经网络架构、智能的搜索策略以及对数学知识的有效组织与运用,使得模型在面对各种数学问题时能够迅速做出反应并给出准确的答案。
(二)精准的题目理解与分析能力
在面对高难度数学题目时,准确理解题目要求与意图是解题的关键第一步。o1 系模型展现出了强大的题目理解与分析能力,能够精准地把握题目中的数学关系、条件限制以及求解目标。通过对自然语言描述的数学问题进行有效的语义解析和逻辑转换,模型将其转化为内部可处理的数学模型与推理任务,从而为后续的解题过程奠定坚实的基础。这种精准的题目理解与分析能力使得模型在处理各种复杂数学表述和逻辑结构时能够游刃有余,避免因误解题目而导致的错误推理。
(三)灵活的推理策略调整
如前文所述,o1 和 o1 pro mode 能够根据题目难度灵活调整推理时间和推理策略。在面对简单题目时,模型采用快速高效的推理方式,迅速得出答案;而在处理复杂难题时,模型则能够自动切换到深度推理模式,增加推理步骤和时间投入,对问题进行全面细致的分析与求解。这种灵活的推理策略调整能力使得模型在不同难度层次的数学问题上均能保持较高的解题效率和准确性,体现了其在推理过程中的智能化与自适应特性。
总结 2:推理模型局限性分析
(一)知识覆盖的局限性
虽然 o1 系模型在本次测试的高中数学竞赛题和考研数学题上取得了较好的成绩,但数学领域知识浩瀚无垠,仍可能存在一些特定的数学分支、理论或特殊题型,模型的知识储备不足或尚未深入学习掌握。例如,在某些高等数学的前沿研究领域、小众的数学应用场景或具有特殊历史文化背景的数学问题上,模型可能会因为缺乏相关知识而无法给出准确的答案或有效的推理。这表明模型在知识覆盖的广度和深度上仍有进一步拓展和完善的空间,需要不断地学习和吸收更多的数学知识,以应对日益复杂多样的实际应用需求。
(二)复杂逻辑推理的挑战
在一些极其复杂的逻辑推理场景中,o1 系模型可能会遇到困难。尽管模型在常规的数学推理任务中表现出了较高的水平,但当面对涉及多层嵌套逻辑、模糊逻辑或高度抽象逻辑的问题时,模型的推理能力可能会受到限制。例如,在一些数学证明题中,需要运用复杂的逻辑推导和反证法等推理技巧,模型可能无法像人类数学家那样进行深入细致的逻辑思考和创造性的推理过程,导致无法成功完成证明或给出完整准确的推理步骤。这反映出模型在处理复杂逻辑关系时的局限性,需要进一步优化其推理机制和逻辑处理能力,以提升在复杂逻辑推理任务中的表现。
(三)可解释性问题
随着人工智能模型在各个领域的广泛应用,其可解释性成为了一个重要的关注点。o1 系模型作为一种基于深度学习的大模型,其推理过程往往具有高度的复杂性和黑箱特性,难以直观地理解和解释模型是如何得出某个答案或推理结果的。这对于一些对可解释性要求较高的应用场景,如数学教育、科学研究中的关键决策等,可能会带来一定的困扰。缺乏可解释性使得用户难以信任模型的输出结果,也不利于模型的进一步优化和改进。因此,如何提高 o1 系模型的可解释性,使其推理过程更加透明、可理解,是未来模型发展需要解决的一个重要问题。
未来展望
通过本次对 o1 系模型的高难度数学测试,我们全面深入地了解了其在数学推理能力方面的表现。o1 系模型在正确率、推理时间以及特殊题目处理等方面展现出了显著的优势,其高效的推理算法、精准的题目理解与分析能力以及灵活的推理策略调整能力使其在众多模型中脱颖而出。然而,模型也存在知识覆盖局限性、复杂逻辑推理挑战以及可解释性问题等不足之处。
展望未来,随着技术的不断发展和研究的深入,我们期待 o1 系模型能够在以下几个方面取得进一步的突破和改进。首先,通过不断学习和更新知识,扩大其知识覆盖范围,提高对各种数学领域和特殊题型的处理能力。其次,优化推理机制,提升复杂逻辑推理能力,使其能够更好地应对具有高度复杂性和抽象性的数学问题。最后,加强对模型可解释性的研究,探索有效的方法和技术,使模型的推理过程更加透明、可理解,增强用户对模型的信任和应用的可靠性。




























