话题背景
最近有道题在厂内热度很高,这是一位来自10年的鹅厂程序员从工作中抽象出来的算法题,来考考大家:
题目是这样的:给定多个已经排序好的数组(从小到大),在每个数组中挑选一个数字,计算这些数字的方差。请找出方差最小的数字组合(可能有多个),并输出方差。举例:[1,3,4,6,7,100 ][28,50,70,102 ][14,76,98 ]
选择的数字组合应该是100,102,98。 方差是2.67,要求性能尽可能的高,避免暴力穷举。
来看看鹅厂工程师们都怎么解这道题吧!

鹅厂工程师的看法

@jk-CDG基础平台负责人▼
PS:简单yy了一个思路,没有验证过,仅供参考方差最小的序列,就是需要所有数离平均值最小,同时,考虑到你这儿的序列都是有序了基本上,可以参考多个有序序列的合并排序思路一样

评论回复:
@bin·IEG
这个移动难度比较大,无法保证向较大的方向移动方差的函数的单调性
@aaron·WXG
如果每次只更新移动一个,且的移动的是ptr_sX值中最小的值的指针,似乎是个好方法? 但是我无法证明这个一定能选到最好的?
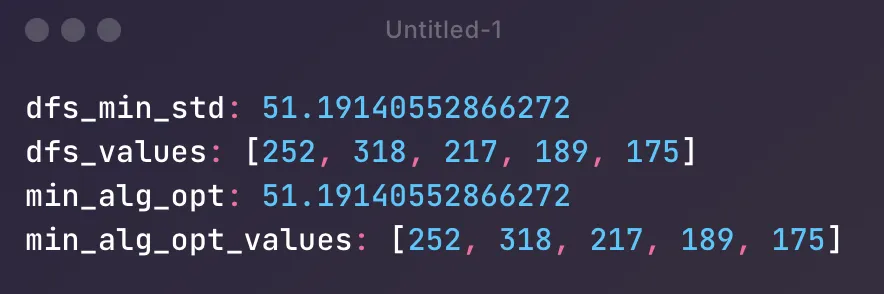
似乎不对,这是反例:
[[252, 638, 754, 848, 887],[318, 384, 533],[31, 81, 105, 123, 203, 213, 217, 298, 536, 562, 603, 605, 624, 651, 850, 855, 918, 921, 950, 951],[189, 474],[175, 348, 416, 419, 525, 743, 807, 986]]
@jk·CDG
这儿每次move不是当前指针的最小值,而是每个指针的下一个值的最小值,这样能保证移动后的平均值影响最小
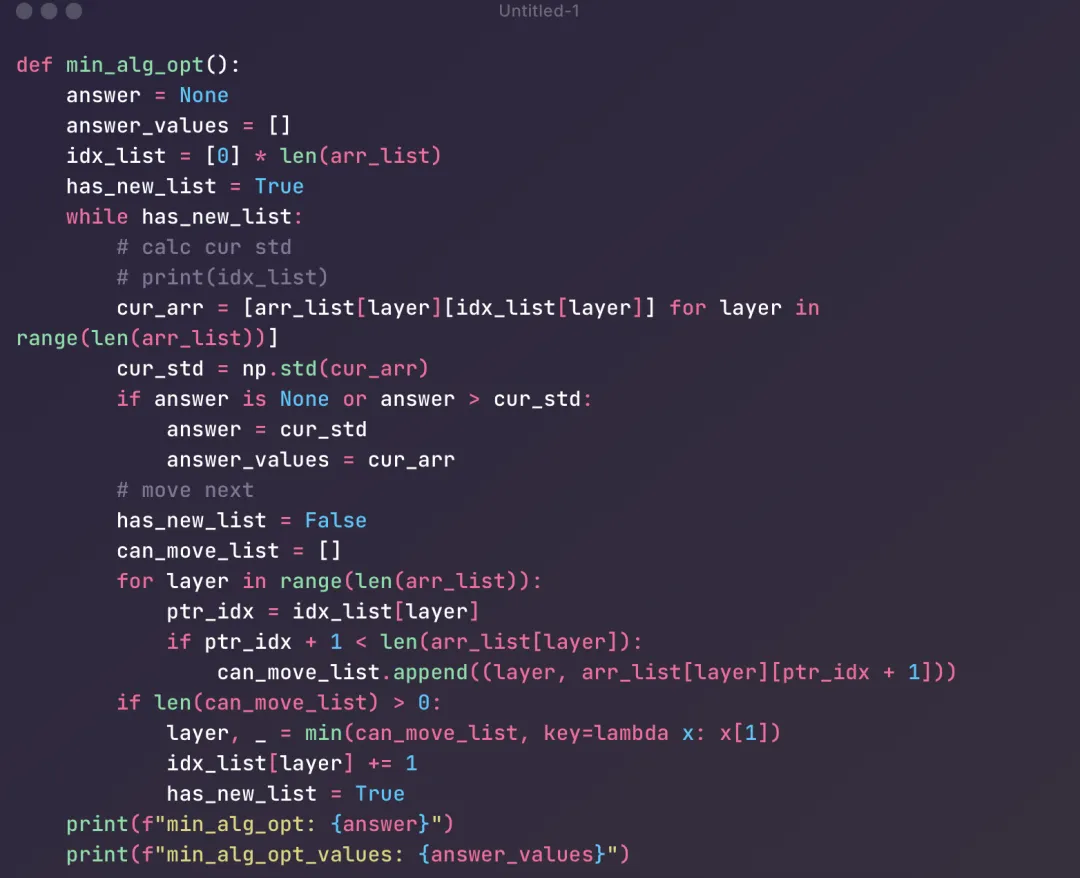
这个case看起来是ok的

@zhenle-IEG开发工程师▼
假如:
- 数组的数量为M
- 数组里面的元素平均个数为N
- 数组里面所有元素的范围为H
两种方式:
第一种:
- 遍历第一个数组的每个元素,对于每个元素通过二分去剩下数组里面找到最接近的元素。
- 还需要对于每个数组进行第1操作。 整体复杂度M^2NLog(N)
第二种:
- 通过计算所有数的最大值和最小值,二分平均数
- 遍历所有数组找最接近平均数的数。整体复杂度Log(H)*Log(N)*M


@rick-IEG应用研究▼
有个想法不知道行不行:
先合并有序数组,O(N),同时纪录合并后有序数组的源数组的index(染色);然后开始滑动窗口,使得窗口内染色数等于数组数,滑的时候更新方差


@mcsh-PCG开发工程师▼
(1) 八皇后问题
- 回溯发遍历取前 N-1 元素求平均 a,算好方差和平均值
- 使用二分查找Arr[N],最左边、最右边、命中,未选中居中选左右两个,更新上面方差和平均值,这部分可优化计算
(2) 楼上 rick 提到滑动窗口法,需要枚举窗口内的组合
如果是10 个数组,每组 10 个元素,按顺序 1-100,滑动窗口滑不动,算法复杂度恶化为穷举


@looker-PCG开发工程师▼
有个二分想法,直接二分方差结果
- 取int_max作为初始方差,遍历每个数组,每个数组取一个接近的数值计算方差
- 后续用这个结果继续二分得到下一个结果,继续遍历每个数组取一个接近的数值重新计算方差
- 重复第二步,退出二分路径


@匿名小伙▼
从网上搜到一个类似的题,题目里只有3个数组。如果是多个,估计就更麻烦了
贴下大致思路:要从三个数组里取x,y,z,使得方差最小,就是找三个离得最近的数。因此我们固定一个数组,去另外两个数组中,一个数组寻找第一个大于等于它的数字,另一个去寻找第一个小于等于它的数字。一共是三个数组,因此一共有六种组合。
以一种组合来举例,假设x<=y<=z,就需要遍历第二个数组(遍历复杂度O(n)),然后在第一个数组里找到比y小的最大值x,在第三个数组里找到比y大的最小值z(二分查找O(logn))。时间复杂度O(nlogn)






























