编辑 | 言征
出品 | 51CTO技术栈(微信号:blog51cto)
Kimi最近太猛了!所有的教育产品感觉都要被颠覆了。
今天,Kimi上线发布一款相当炸裂的AI功能——视觉思考模型k1。可以说颠覆了“K12赛道”的传统搜题解题的产品!
小编惊呼:有了Kimi,学生们还需要手机里安装各种拍照搜题找答案的软件吗?可以预想到,从幼儿园到大学,整个教育赛道恐怕要掀起一股惊涛骇浪!
Kimi,果真越来越“学霸”了!话不多说,直接上干货。
光看这个名字“k1”,就能让大家联想到1个月前kimi推出的对标OpenAI o1系列的 k0-math模型,自然是类o1模型的重大升级。的确是这样,官方介绍道:视觉思考模型k1,同样是强化学习技术打造,但不同的是——
这次的k1模型原生支持端到端图像理解和思维链技术,并将能力扩展到数学之外的更多基础科学领域。
简单理解,这次的k1有两点创新:一是原生支持端到端的图像理解,二是数理化难题全都能拿下了!
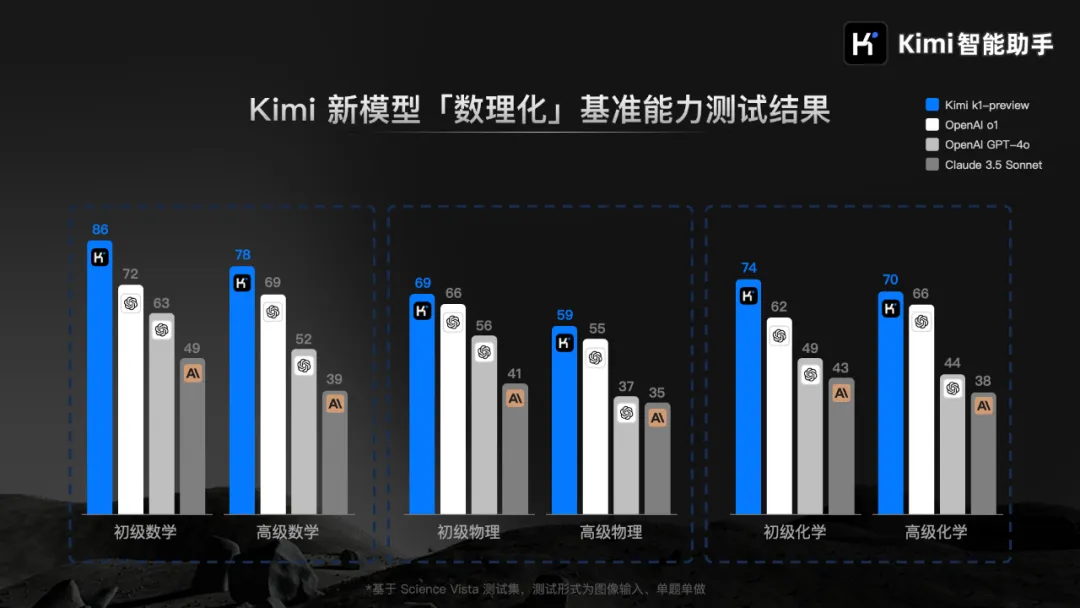
在数学、物理、化学等基础科学学科的基准能力测试中,初代 k1 模型的表现超过了全球标杆模型 OpenAI o1、GPT-4o以及 Claude 3.5 Sonnet。
 图片
图片
1.Kimi实测,当之无愧的大模型学霸
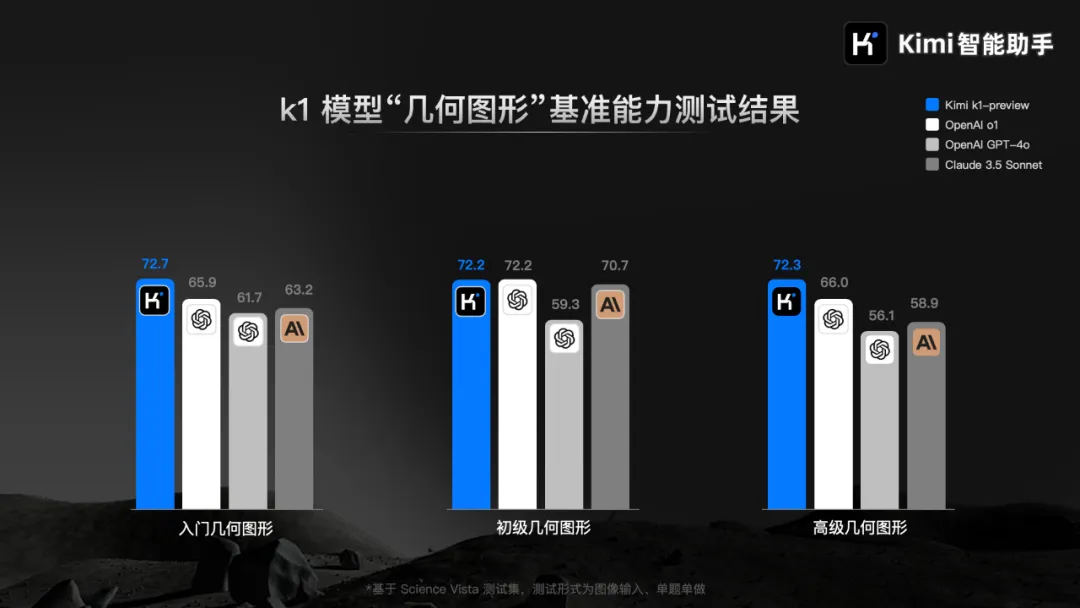
上个月,清华学霸杨植麟冷不防就丢出了k0-math模型,各种奥数级别的难题都可以解决,但也存在不足:由于主要支持LaTeX等格式的文本输入,依赖图形理解能力的部分几何图形题则难以应对。
不过现在,这个问题在k1视觉思考模型就解决了。借助端到端的图像理解能力,解锁了包括几何图形题在内更加全面的数学能力。
 图片
图片
在不同阶段的几何和图形题专项基准能力测试中,k1-preview 成绩追平或超过了 OpenAI 的 o1 模型。
kimi有测试一道普通几何题,
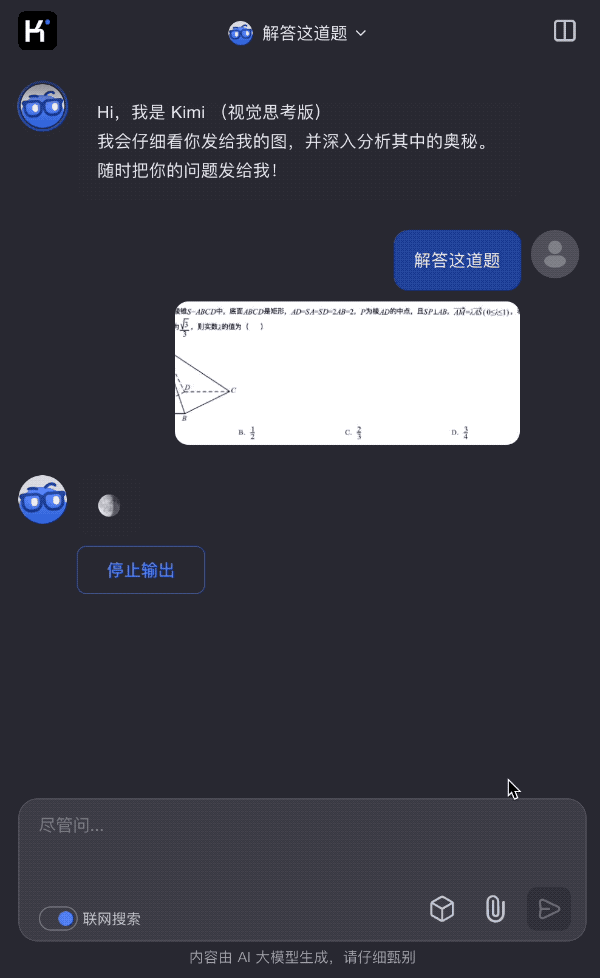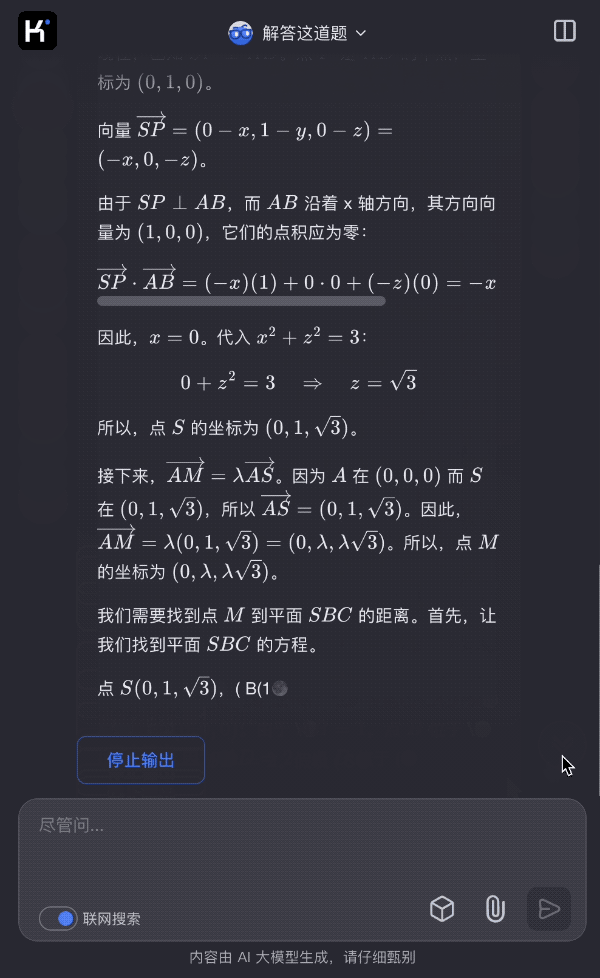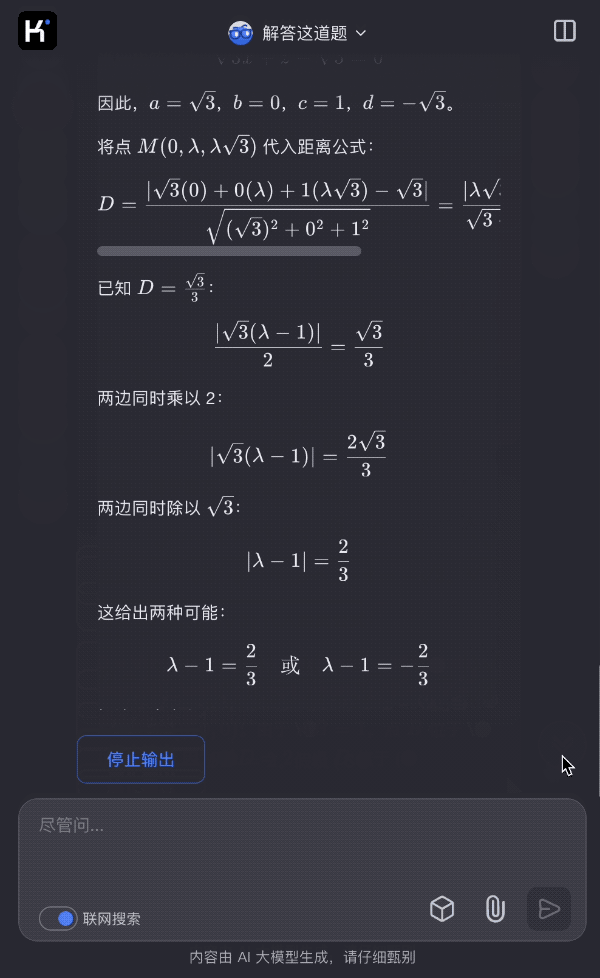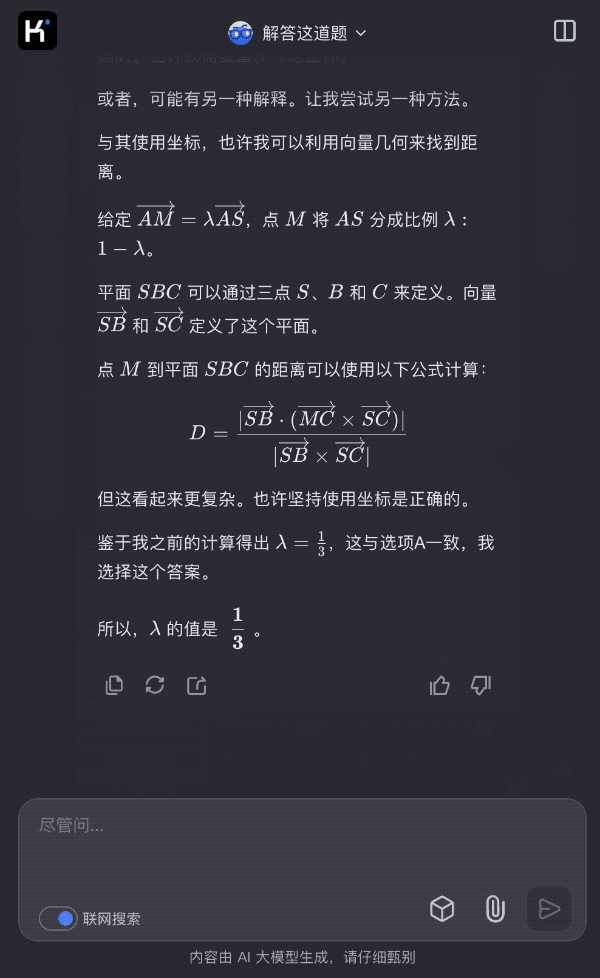 图片
图片
这当然还不算完,除了算几何题,学霸自然是文理全通,数理化都得不在话下。
除了数学能力,k1视觉思考模型将能力扩展到了物理、化学等领域。在基础科学学科教育阶段(这不就是K12嘛)的物理和化学能力测试中,k1 模型的表现同样不输全球领先的玩家 OpenAI 和 Anthropic。
我们来看一道 k1 视觉思考模型解答经典物理电路题的例子:
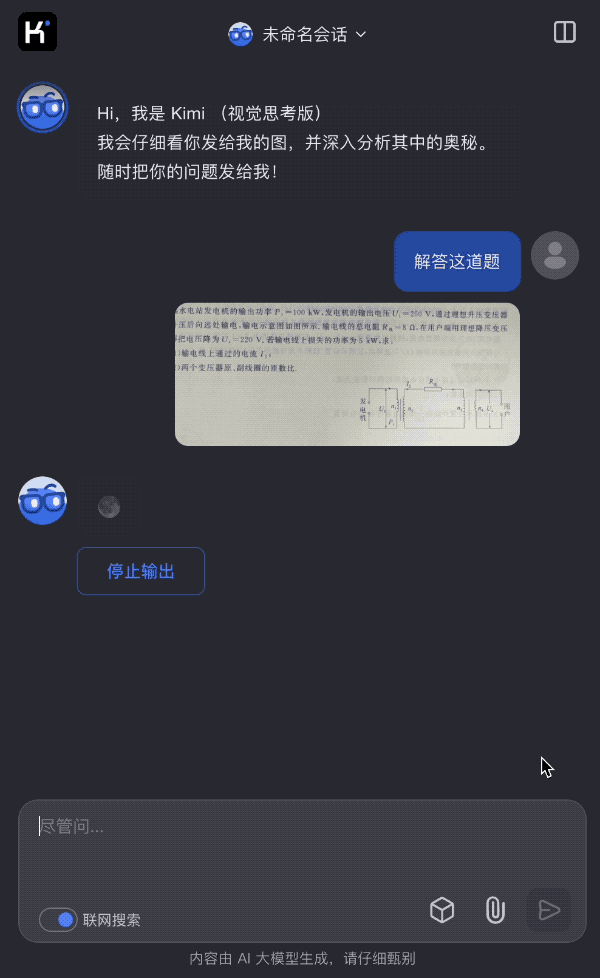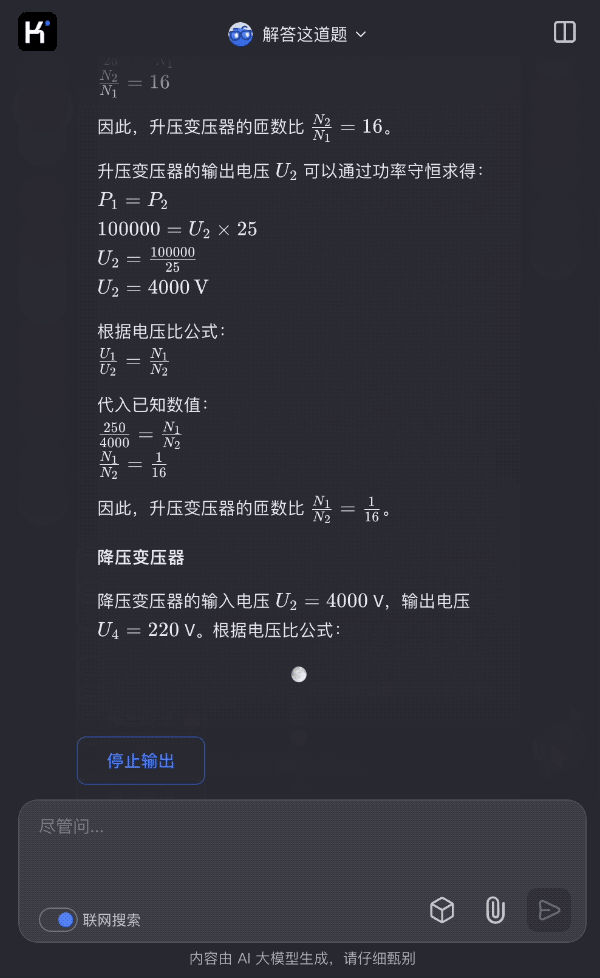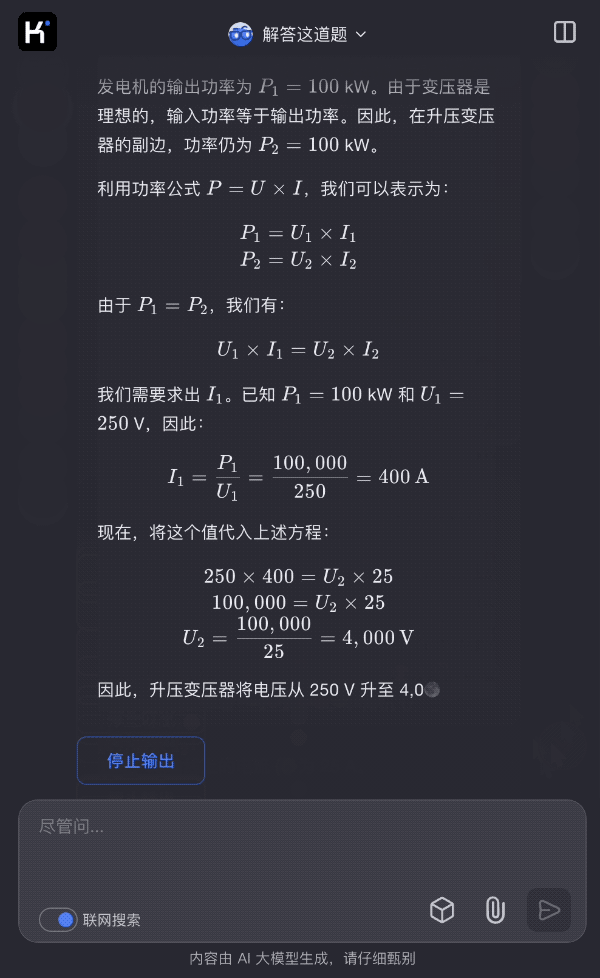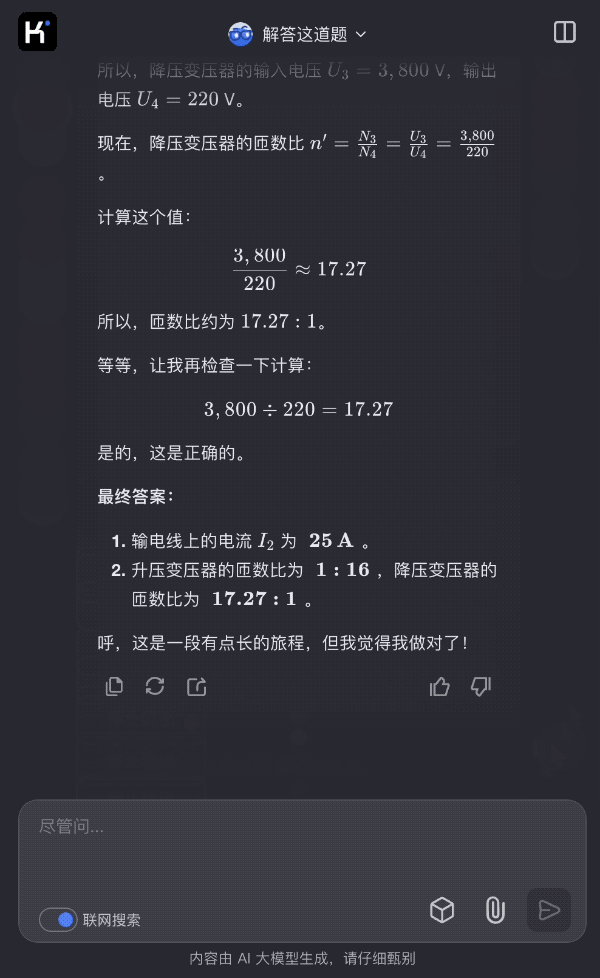 图片
图片
再来个化学题目,kimi的同学将一张曾获得诺贝尔化学奖的技术原理图去掉大部分文字说明,只留下“QD”两个字母,看 k1 是如何一步一步分析出原理图是在讲什么。
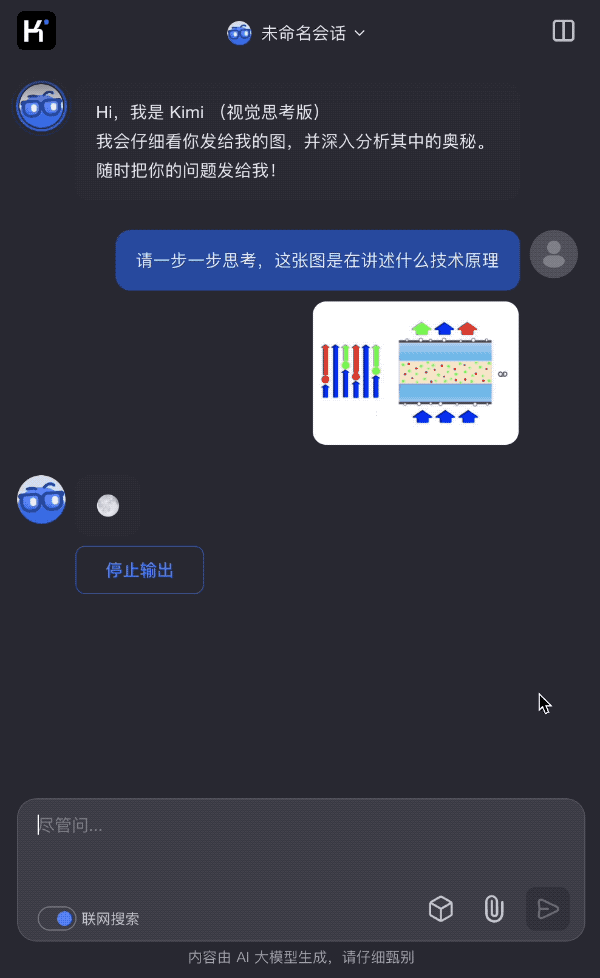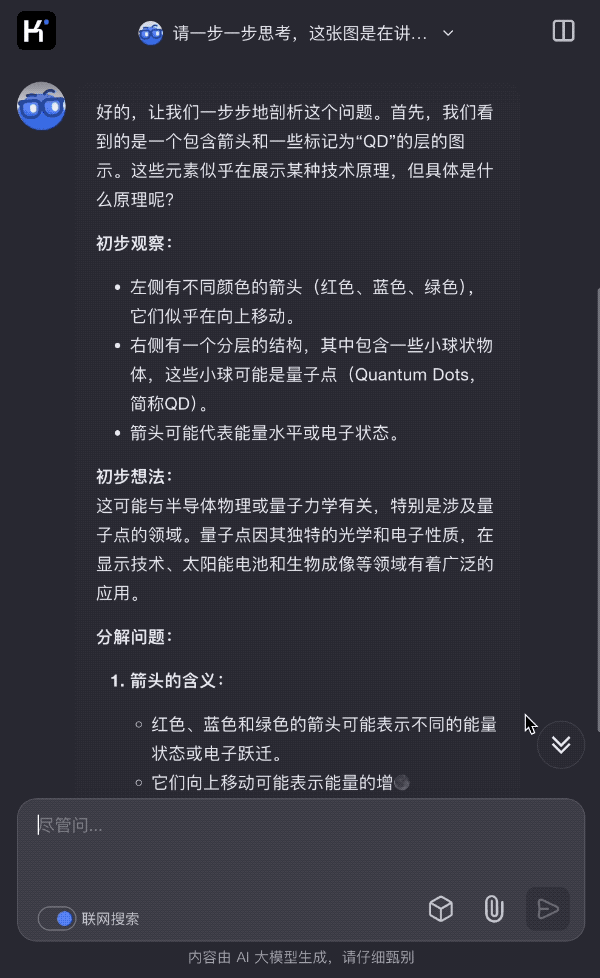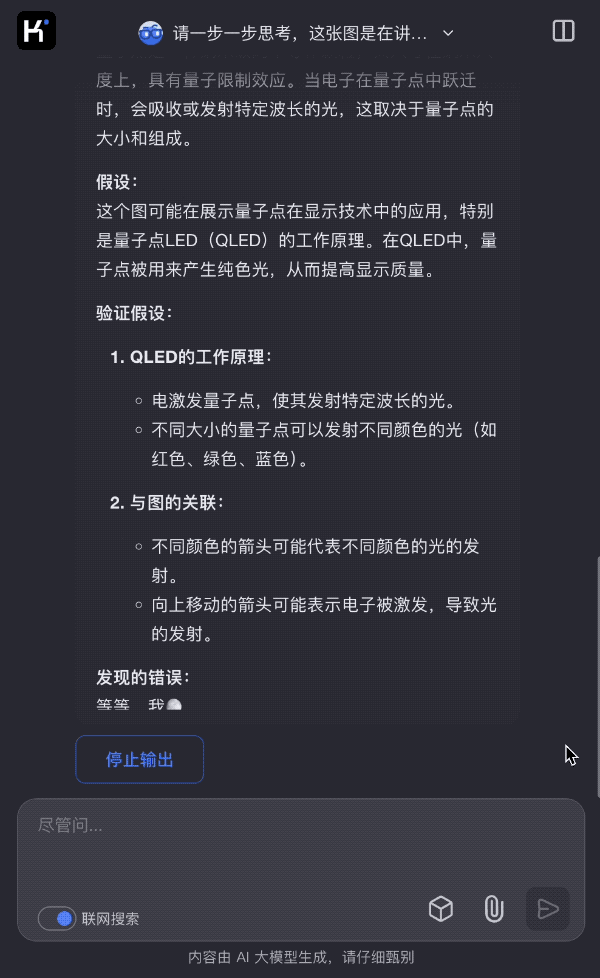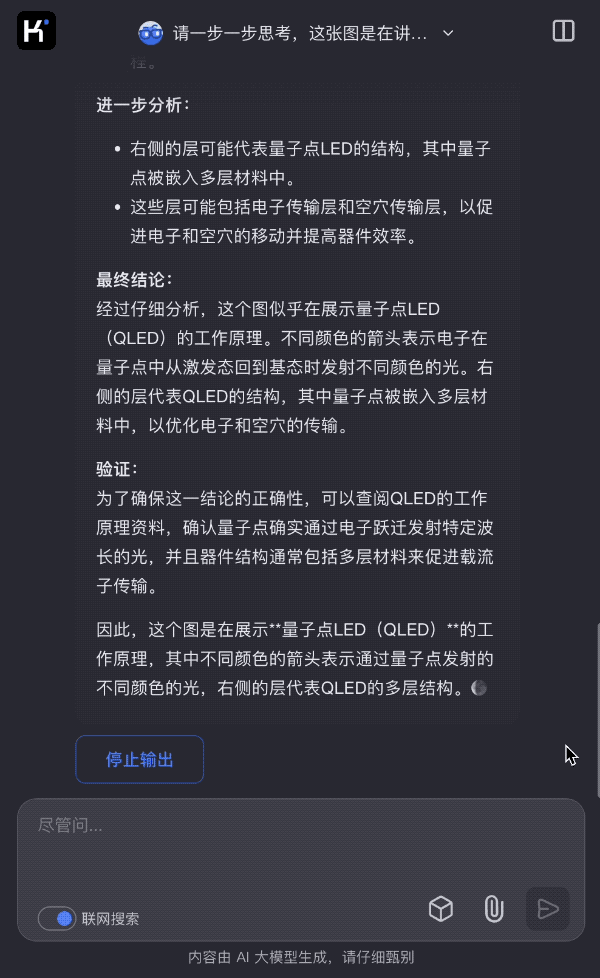 图片
图片
小编实测了下,果真是学霸,大学物理也被Kimi搞定了!一个电荷电场的计算难题——
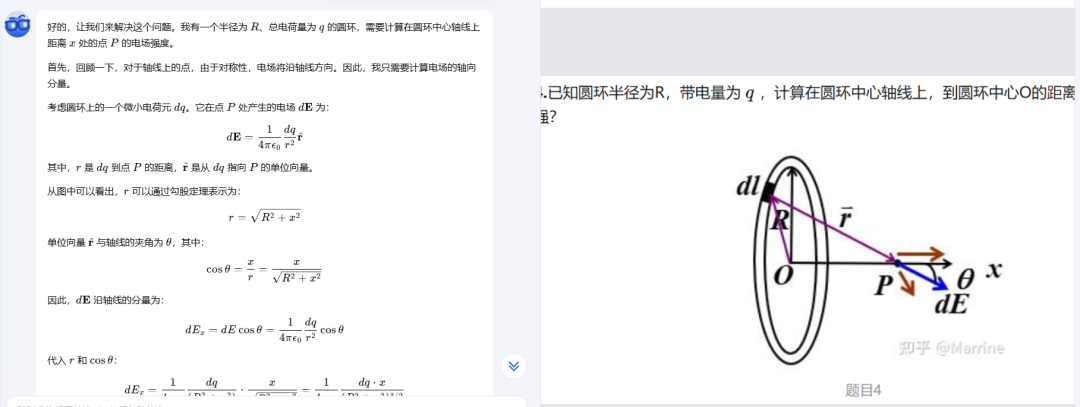 图片
图片
 图片
图片
最后自己被自己感动了,还不失淘气的说:真是令人欣慰呀!
2.大模型理解图像,如何做到的?
之前拍照搜题更多采用的是视觉理解模型,图像分割和图像识别等技术,当然效果也不错,但也存在很多问题。比如,这种技术要求拍照或者照片的内容的质量要足够高,亮度不能太暗,如果是手写,字迹也不能潦草。
但用了k1模型,就不用在顾忌这些了,完全“端到端”的解决!
不用再担心自己拍照技术不够硬、给大模型输入的素材不够清晰!包括照片灰暗、图像模糊、多题一起拍、手写字迹干扰、纯手写的题目、倾斜的拍摄角度等问题,k1这回一下都解决了!
 图片
图片
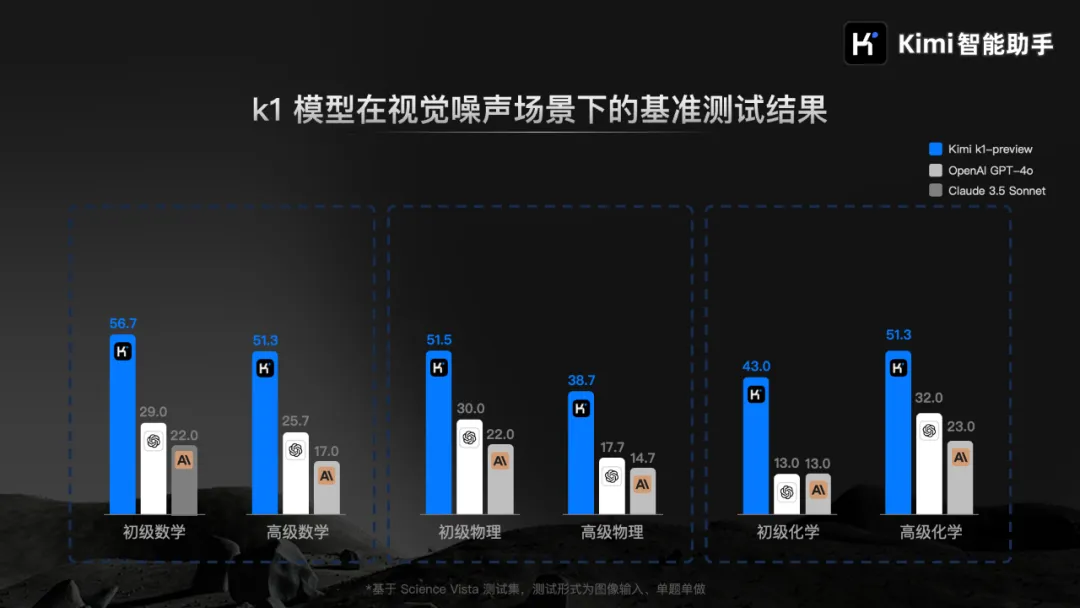
Kimi专门测试了更接近真实使用场景的 k1 模型表现。在“噪声”场景下,多项基准测试数据显示,k1 模型相比OpenAI 和 Anthropic 的视觉语言模型,有更显著的领先优势。
数据显示,其他大部分模型在视觉噪声场景下,能力水平下降了一半多,k1 则依靠超强的视觉识别能力,保持了最低的能力损失幅度。
 图片
图片
我们来看一个例子。
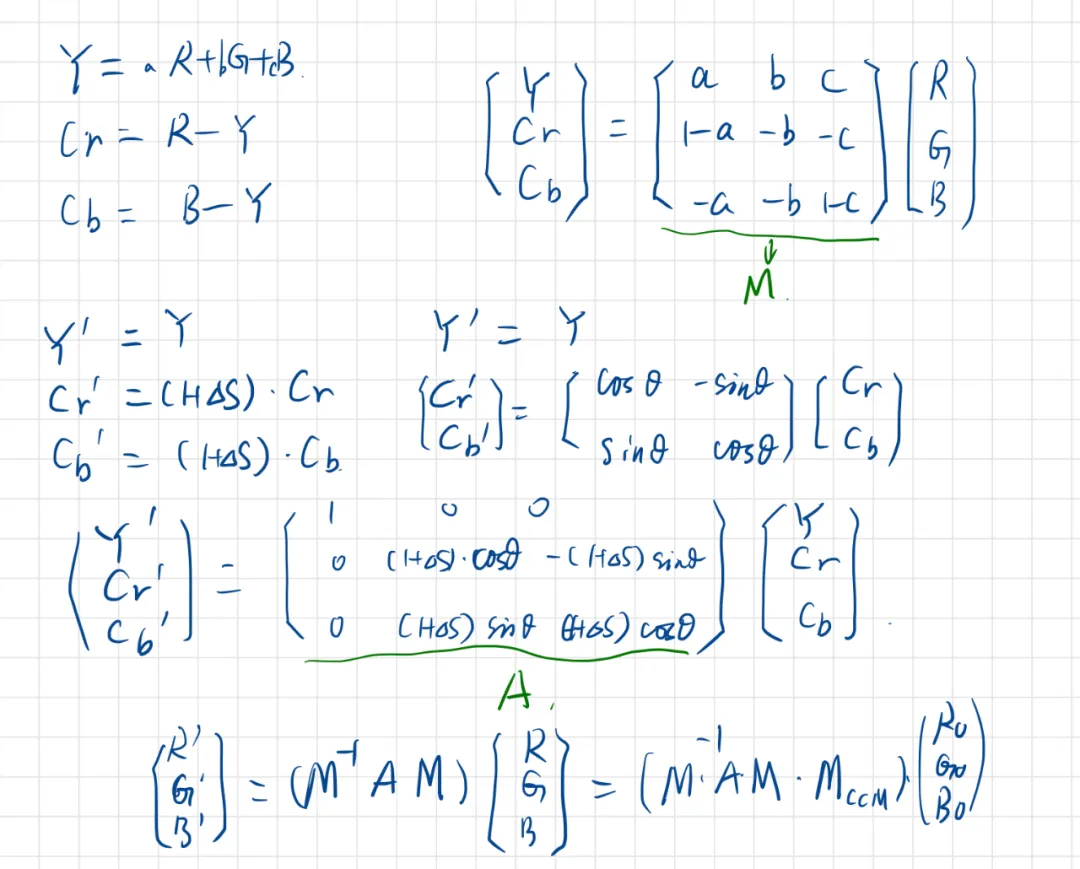
下图是一位月之暗面的同事在平板电脑上手动推演的公式。
 图片
图片
看看 k1 模型是怎么一步一步分析出作者意图的。
 图片
图片
3.实测K1:李永乐线性代数笔记
眼见未必为实,小编自然要实际操练一下,赶紧从网上找了一份自己多年不看的李永乐的线性代数笔记,这笔记的字迹实在是有点让人看不清,不过既然是考验k1,用它最合适。
 图片
图片
kimi,快帮我看看上面都有哪些数学知识点?
 图片
图片
结果果然令人满意,不仅一字不差地给出了笔记照片中的文字内容——
 图片
图片
还梳理了这张手写笔记涉及的数学知识点,包括:
怎么弄判断矩阵排列的奇偶性、如何按排列展开行列式、高阶行列式的计算方法等等。
 图片
图片
可能会有人说,思维链、图像理解的能力,这些并不新鲜,年初就有了。但思维链+端到端的图像理解对于大模型而言,Kimi这次绝对是一个“aha”级别的创新!
4.惊喜——让大模型具备数理化思维回答问题的能力找到《荷马史诗》、《几何原本》的作者
学霸的厉害之处,不仅可以做题拿高分,更重要的是可以用数理化思维和视角去看待和解决和回答生活中遇到的问题,一般人可没这个能力。
据介绍,在发布k0-math时,月之暗面就发现 Kimi 数学版不只会做数学题,它还会用数学思维来解释任何问题。比如你问“一颗心值多少钱”,Kimi 数学版经过一番分析,可能给出让我们惊喜的答案:一颗心是无价的。
这次视觉思考模型k1,在学习了代数、几何、物理、化学、生物等更多基础科学的难题之后,同样涌现出更多通用能力。
小编为此设置了两道难题,来考验k1的数理化思维。
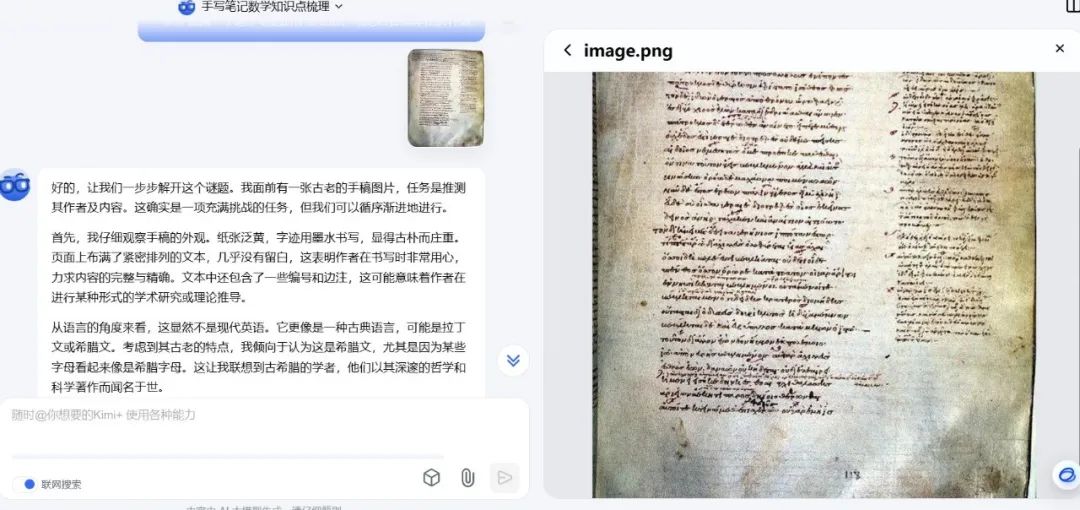
第一个是,识别一张“荷马史诗”的手写残页,然后给出作者和作品是谁。
 图片
图片
可以说想法步骤都没问题,首先看手稿外观、再看语种是希腊语、在进一步分析手稿中的文字里提到的词汇,来判断出可能是在公元前5世纪至公元2世纪之间写成的,最后锁定是亚里士多德的自然哲学或者数学著作。
不过这个结果是错误的,这说明Kimi对于希腊文学的知识储备还需要继续精进一下,当然也存在小编这次的照片实在太过模糊的问题。
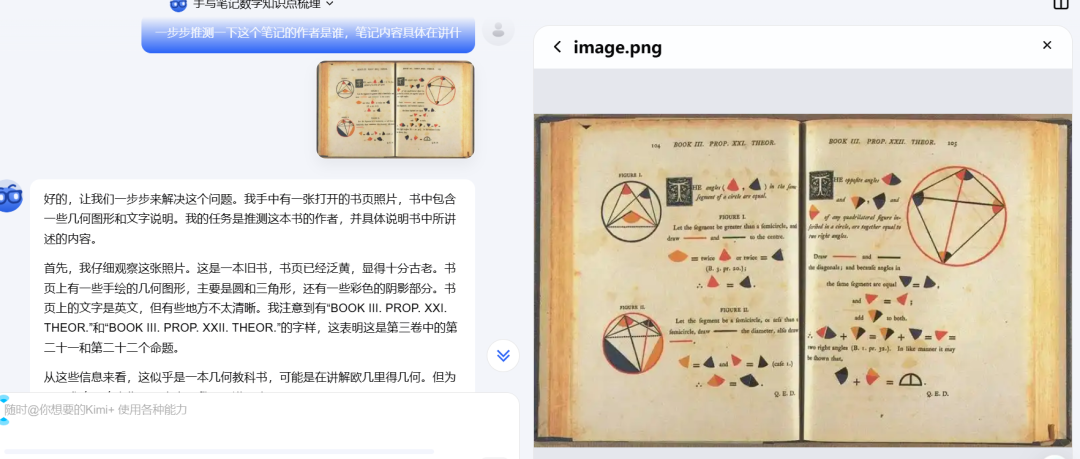
第二个则是几何原本的问题,小编在网上找到一份几何原本的手稿照片,发给 Kimi 视觉思考版,看它如何一步一步,引人入胜地推理,这次不失所望,推理成功!
 图片
图片
 图片
图片
5.写在最后:Kimi也许会颠覆K12赛道
这次k1模型的模型,真的可以说是对于月之暗面来说意义不同寻常。从下半年月之暗面k0-math的发布再到底层推理架构的开源,再到此次k1模型的发布,我们看到了一个从追赶OpenAI的Kimi正在发生新的变化:
Kimi似乎在追赶中找到了很多产品的创新,也找到了更多适合中国土壤的大模型产品的赛道和方向,k0解决数学强化推理、k1解决K12教育的拍照搜题解题的难题,这次实测,也让小编看到了以Kimi为代表的大模型在重构教育互联网产品的极大的可能。
但小编认为,这种能力还可以泛化,因为就在刚刚,我还用k1帮忙读了非常专业的AI技术报告——我在微软刚推出的phi-4模型报告中,找到一个复杂的图表,可以直接丢给Kimi,请帮忙解读。
k1给出了正确的最终结论:
关键token是指那些使成功概率变化≥0.2的token,用方框标出,并带有表示概率变化的下标。它们与低概率token(概率≤0.1,用下划线标出)不同,因为关键token对整体成功有显著影响,而不仅仅是概率低。

所以Kimi的持续创新,带来的想象空间将会越来越大,不止K12的拍照搜题,所有知识类的工具可能都会被k1重塑!
最后,正如网友所说:Kimi,大模型国产之光,加油!