Python 时序预测常用方法代码实现-51CTO.COM

时序预测是根据历史数据来预测未来一段时间内的数据。Python 中常用的时序预测方法包括：移动平均法（Moving Average, MA）、指数平滑法（Exponential Smoothing, ES）、自回归模型（Autoregressive Model, AR）、自回归移动平均模型（Autoregressive Moving Average Model, ARMA）以及自回归积分移动平均模型（Autoregressive Integrated Moving Average Model, ARIMA）。

1. 移动平均法（MA）

移动平均法通过计算一定时间窗口内数据的平均值来进行预测，适用于平稳序列。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.api import SimpleExpSmoothing
# 生成模拟数据
np.random.seed(0)
data = np.random.randn(100).cumsum()
df = pd.DataFrame(data, columns=['value'])
# 检查数据是否平稳
result = adfuller(df['value'])
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {result[1]}')
# 绘制原始数据
df.plot()
plt.title('原始数据')
plt.show()
# 创建移动平均模型
window_size = 5
df['moving_average'] = df['value'].rolling(window=window_size).mean()
# 预测下一轮数据
last_window = df['value'][-window_size:].values
forecast = np.mean(last_window)
print(f"下一个时间点的预测值: {forecast}")
# 绘制预测结果
plt.figure(figsize=(12, 6))
plt.plot(df['value'], label='原始数据')
plt.plot(df['moving_average'], label='移动平均值', color='orange')
plt.axhline(y=forecast, color='red', linestyle='--', label='预测值')
plt.legend()
plt.title('移动平均法预测')
plt.show()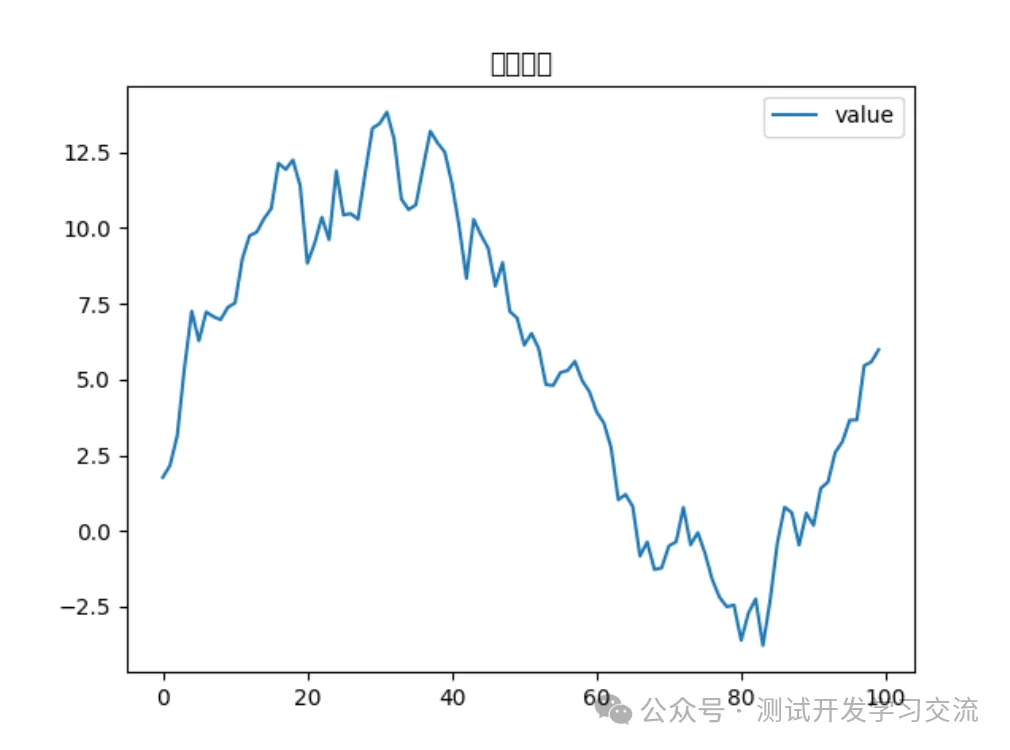

2. 指数平滑法（ES）

指数平滑法通过对历史数据赋予不同的权重，距离预测点越近的数据权重越大，适用于非平稳序列。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.holtwinters import ExponentialSmoothing
# 生成模拟数据：正弦波加上随机噪声


np.random.seed(42)
dates = pd.date_range('20230101', periods=100)
data = np.sin(np.linspace(0, 2 * np.pi, 100)) + np.random.normal(0, 0.1, 100)
df = pd.DataFrame(data, index=dates, columns=['Value'])
# 定义并拟合指数平滑模型
model_es = ExponentialSmoothing(df['Value'], trend='add', seasnotallow='add', seasonal_periods=4)
fit_model_es = model_es.fit()
# 预测下一轮数据
forecast_es = fit_model_es.forecast(5)
# 画图展示原始数据和预测结果
plt.figure(figsize=(12, 6))
plt.plot(df['Value'], label='原始数据')
plt.plot(fit_model_es.fittedvalues, label='拟合值', color='green')
plt.plot(forecast_es, label='预测值', color='red')
plt.legend()
plt.title('指数平滑法预测')
plt.xlabel('日期')
plt.ylabel('值')
plt.grid(True)
plt.show()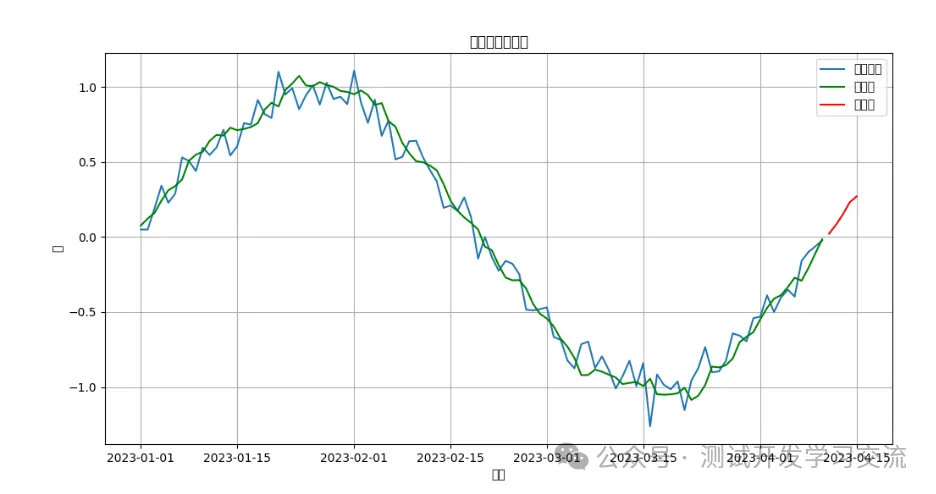

3. 自回归模型（AR）

自回归模型是一种线性预测模型，它使用时间序列的过去值作为未来值的预测因子。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
# 生成自回归过程的模拟数据
from statsmodels.tsa.arima_process import ArmaProcess


np.random.seed(42)
ar_params = [0.8]
arma_process = ArmaProcess(ar=ar_params)
simulated_data = arma_process.generate_sample(nsample=250)
dates = pd.date_range('20230101', periods=250)
df_arma = pd.Series(simulated_data, index=dates)
# 定义ARIMA模型，这里p=1表示一阶自回归
model_ar = ARIMA(df_arma, order=(1, 0, 0))
# 拟合模型
model_ar_fit = model_ar.fit()
# 进行预测，预测未来10个时间点的数据
forecast_ar = model_ar_fit.forecast(steps=10)
# 画图展示原始数据和预测结果
plt.figure(figsize=(12, 6))
plt.plot(df_arma, label='历史数据')
plt.plot(pd.date_range(dates[-1], periods=10, freq='D'), forecast_ar, label='预测值', color='red')
plt.legend()
plt.title('自回归模型预测')
plt.xlabel('日期')
plt.ylabel('值')
plt.grid(True)
plt.show()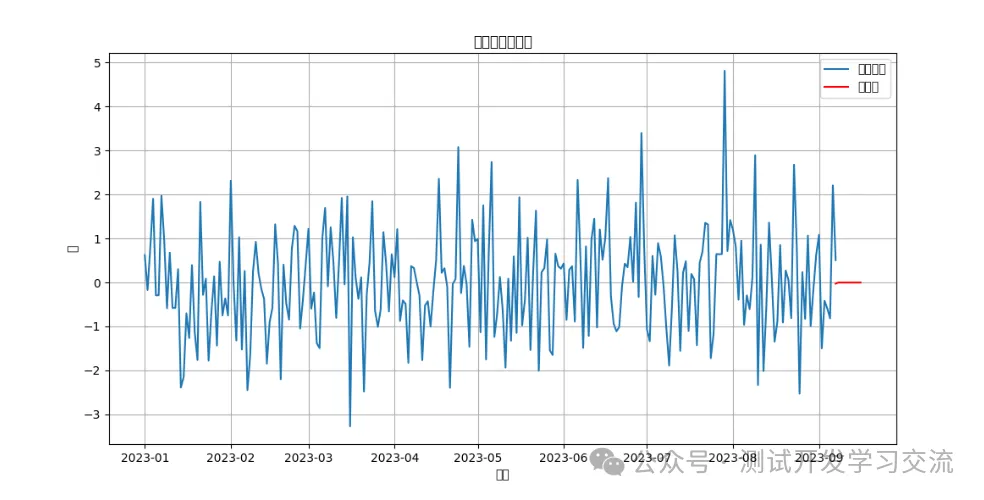

4. 自回归移动平均模型（ARMA）

ARMA模型结合了AR和MA模型的特点，使用时间序列的过去值和误差项的过去值作为未来值的预测因子。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_process import arma_generate_sample
from statsmodels.tsa.arima.model import ARIMA
# 生成ARMA过程的模拟数据
np.random.seed(42)
ar_params = [1, -0.5]
ma_params = [0.7, -0.3]
dates_arma = pd.date_range('20230101', periods=100)
arma_data = arma_generate_sample(nsample=100, ar=ar_params, ma=ma_params)
df_arma = pd.Series(arma_data, index=dates_arma, name='Value_ARMA')
# 定义并拟合ARMA模型
model_arma = ARIMA(df_arma, order=(1, 0, 2))
fit_model_arma = model_arma.fit()
# 预测下一轮数据
forecast_arma = fit_model_arma.predict(start=len(df_arma), end=len(df_arma)+4, typ='levels')
# 画图展示原始数据和ARMA预测结果
plt.figure(figsize=(12, 6))
plt.plot(df_arma, label='原始数据')
plt.plot(forecast_arma, label='预测值', color='purple')
plt.legend()
plt.title('ARMA模型预测')
plt.xlabel('日期')
plt.ylabel('值')
plt.grid(True)
plt.show()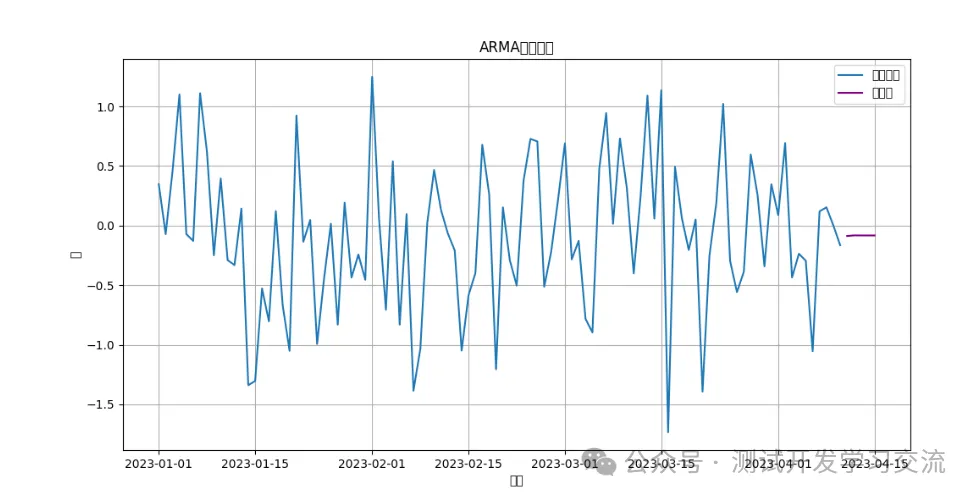

5. 自回归积分移动平均模型（ARIMA）

ARIMA模型是在ARMA模型的基础上增加了差分操作，使得非平稳序列可以通过差分变为平稳序列。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
# 生成非平稳的模拟数据
np.random.seed(42)
data = np.random.randn(100).cumsum()
df = pd.DataFrame(data, columns=['value'])
# 定义ARIMA模型，这里p=1, d=1, q=1
model_arima = ARIMA(df['value'], order=(1, 1, 1))
# 拟合模型
model_arima_fit = model_arima.fit()
# 进行预测，预测未来10个时间点的数据
forecast_arima = model_arima_fit.forecast(steps=10)
# 画图展示原始数据和预测结果
plt.figure(figsize=(12, 6))
plt.plot(df['value'], label='历史数据')
plt.plot(pd.date_range(df.index[-1], periods=10, freq='D'), forecast_arima, label='预测值', color='red')
plt.legend()
plt.title('ARIMA模型预测')
plt.xlabel('日期')
plt.ylabel('值')
plt.grid(True)
plt.show()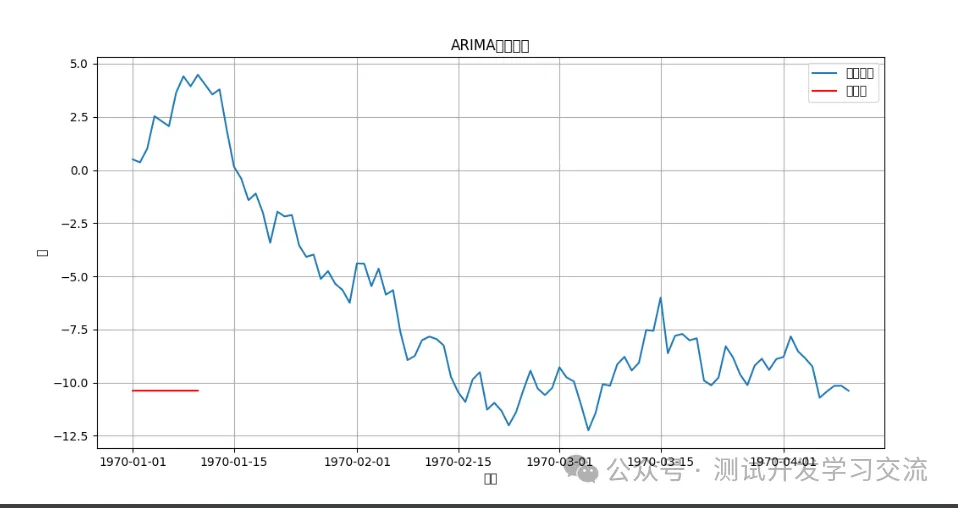

注意事项

选择合适的预测方法：根据数据的特点和需求选择合适的预测方法，如平稳序列可以选择AR、MA或ARMA等，非平稳序列可以选择ARIMA等。

数据预处理：在进行时序预测之前，需要对数据进行预处理，如去除异常值、填充缺失值等。

参数调整：在实际应用中，可能需要调整模型的参数以获得更好的预测效果，如调整移动平均的时间窗口大小、指数平滑的平滑系数、ARIMA模型的阶数等。

模型诊断：通过残差分析、AIC/BIC等指标来评估模型的性能，并进行必要的调整。

总结

时序预测是数据分析中的一个重要领域，Python 提供了丰富的库和工具来实现各种时序预测方法。本文详细介绍了四种常用的时序预测方法及其在 Python 中的实现，希望这些示例能帮助你更好地理解和应用时序预测技术。如果有任何其他问题或需要进一步的解释，请随时提问。