本工作被人工智能顶级会议 NeurIPS 2024 接收。在诸如推荐系统、展示广告等多数实际应用中，所收集的数据往往包含缺失值，并且这些缺失值通常并非随机缺失，这会使模型的预测性能变差。一些现有的估计量和正则化器试图实现无偏估计以提升模型的预测性能。然而，当倾向得分趋于零时，这些方法的方差和泛化误差界通常是无界的，从而损害了它们的稳定性和鲁棒性。在本文中，我们首先从理论上揭示了正则化技术的局限性。此外，我们进一步阐明，对于广义形式的估计器，其无偏性必然会导致方差和泛化误差无界。这些一般性规律启示我们，预估模型的设计并非仅仅关乎消除偏差、减小方差或者简单地实现偏差-方差的权衡。我们基于这些理论发现，从一个全新的视角重新审视对于非随机缺失数据预估建模的本质——偏差和方差的定量联合优化。网商银行智能营销团队提出细粒度动态学习框架来联合优化偏差和方差，该框架能够依据预先定义的目标函数为每个用户-商品对自适应地选择合适的估计器。通过这种操作，模型的泛化误差界和方差降低并从理论层面保证了预估模型方差和泛化误差有界，进一步提高模型在随机缺失数据上的泛化能力。
论文题目：Fine-Grained Dynamic Framework for Bias-Variance Joint Optimization on Data Missing Not at Random
论文连接：https://openreview.net/forum?id=gLoe70Tn8V&referrer=%5BAuthor%20Console%5D(%2Fgroup%3Fid%3DNeurIPS.cc%2F2024%2FConference%2FAuthors%23your-submissions)
一、纠偏推荐背景介绍
在几乎所有的实际应用场景中，我们所收集的数据存在一定概率的部分缺失情况。具有相同缺失概率的特殊情形被称为随机缺失（MAR）。然而，在在线推荐、搜索和展示广告领域，存在大量非随机缺失（MNAR）的点击、转化和评级记录，样本缺失的概率各不相同，即存在倾向性。例如，在推荐系统中，用户通常会点击他们可能购买的物品，而对购买意愿较低的其他物品则予以忽略。因此，所观察到的点击和转化数据属于 MNAR 类型，并非代表性样本。当使用 MNAR 数据来训练模型时，该模型在 MAR 数据上的预测表现通常难以令人接受。这是因为 MNAR 数据给预测模型引入了样本选择偏差。
为了消除样本选择偏差，研究人员提出了许多偏差校正的估计器（如基于误差插补的（EIB）方法、逆倾向加权（IPW/IPS）技术、双重鲁棒（DR）方法等）。然而，在几乎所有的偏差校正方法中，较小的倾向性导致了高方差和泛化误差界。因此，研究者提出了各种方法来降低估计方差并提高模型稳定性。尽管如此，当倾向性趋于零时，它们仍然具有无穷的方差和泛化边误差界，这对于模型的泛化性能会产生较大的影响。对于由小倾向性引起的高方差和泛化边界，一些方法通过牺牲无偏性而采用归一化技术，例如，归一化 IPS（SNIPS），稳定 DR（SDR）。此外，之前的大多数工作只关注通过设计估计器或正则化器来减少方差或消除偏差，而忽视了估计器设计中偏差-方差的关系和本质。
二、正则化技术和目前纠偏估计器的局限性
非随机缺失数据
定义用户集合和商品集合为 U={u_1,u_2,⋯,u_M }和 I={i_1,i_2,⋯,i_N }。所有用户-商品对的集合表示为 D=U×I，标签矩阵和预估矩阵表示为 Y∈R^(M×N)和 Y ̂∈R^(M×N)，其中预测任务包含用户评分预估，点击率（CTR）预估，转化率（CVR）预估等。Y 和 Y ̂ 中的每个元素〖yu,i〗和 y ̂_(u,i)为用户 u 对商品 i 真实标签和预测输出。一般情况下，标签矩阵 Y 不可能被全部观测到。样本被观测的变量表示为 o_(u,i)∈{0,1}，考虑到无缺失样本的情况，则的预测不准确度定义为：
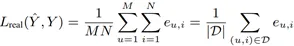
其中，e_(u,i) 为预测误差。预测问题的目标是最小化上述预测不准确度 L_real。事实上，只有观测标签集合 Y^O 能被用于建模。朴素预估方法通过建立模型最小化如下所示的预测不准确度。
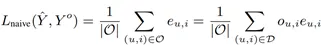
如果每个样本缺失的概率相同，那么上述的朴素预估方法是无偏的。但是，如果使用的样本是 MNAR 的，那么上述估计器是有偏的。
考虑到 MNAR 数据带来的样本选择偏差问题，研究人员提出各种无偏估计方法来克服这个问题，如：EIB，IPS/IPW，DR，以及它们的各种变体。EIB、IPS、DR 估计器的损失函数如下所示：
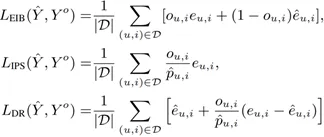
其中，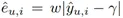
为缺失数据的 MAE 插补误差，
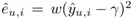为缺失数据的MSE插补误差，w 和 γ 为超参数。p ̂_(u,i) ϵ(0,1) 为倾向性分数。对于朴素估计器、EIB、IPW/IPS、DR 方法的偏差和方差公式由下表给出。
其中，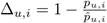
，
。
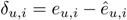通常来说，插补误差预估模型的学习也涉及到 MNAR 问题。一些联合学习算法，如 DR-JL 等，使用倾向模型来克服这个问题。因此，倾向性估计在无偏性和稳健性方面具有关键作用。此外，很难准确估计所有用户-物品对的插补误差，因此很难实现 EIB 估计器的无偏性。如果倾向性估计 p ̂_(u,i) 是准确的，即 p ̂_(u,i)=p_(u,i)，那么 IPS 和 DR 估计器是无偏的。实际应用中，对于一个新的数据集，我们无法事先知道该数据集中倾向概率的范围。因此，一个新的数据集可能会引入极小的倾向概率导致 IPS 和 DR 的方差非常大，这将破坏估计器预估性能的稳定性，尤其是对于较大的数据集。这对于实际工业场景是不可接受的。根据表格中给出的各个估计器偏差方差的表达式，倾向性越小，方差越大。当倾向性分数趋于零时，方差趋于无穷大。同样，其他基于 IPS 和 DR 的无偏估计方法的方差也是无界的。另一方面，虽然在预测误差 e_(u,i) 是有界时，朴素方法和 EIB 方法的方差是有界的，但要实现无偏估计却很困难，甚至是不可能的。
正则化技术和静态估计器的局限性
定义具有正则化的估计器的一般形式为：
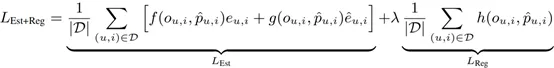
其中，函数 f(∙,∙)≠0 满足 f(0,p ̂_(u,i) )=0，g(∙,∙) 和 h(∙,∙) 是关于 o 和 p ̂_(u,i) 的函数。〖LEst〗和 L_Reg 分别是估计器和正则化器的预测不准确性，对于所有的用户-商品对，它们满足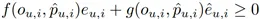
和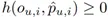
。λ>0 为标量权重。上述表达式给出的估计器的一般形式 L_Est 涵盖了现有的大部分估计器，涉及 EIB、IPS、DR、MRDR、TDR、MIS、IPS/DR-SV 以及其他基于 IPS 和 DR 方法的估计器。另一方面，几乎所有现有的正则化设计，包括 SV、MIS、BMSE 等正则化方法，都可以转化为 L_Reg 给出的一般形式。在以前的工作中，正则化技术在一定程度上降低了估计器的方差并改善了泛化性能。然而，它仍然有一些不可避免的局限性（相关理论细节及其证明，参见原论文 3.1 节）：
- 对于具有正则化项的一般估计器 L_(Est+Reg)，在不牺牲无偏性的同时减少方差是不可能的。
- 正则化方法 L_Reg 无法保证估计器方差和泛化误差是有界的。
根据之前的研究工作和本工作得到的理论结果，正则化技术在一定程度上可以减少方差，但不能使估计器具有有界方差和泛化误差界。或者说，正则化技术对改善模型预测和泛化性能的影响是有限的。
对于估计器 L_Est，大量的方法追求无偏估计或者追求估计方差的减少，再或者通过手动设计估计器来实现偏差和方差的简单折衷。本工作我们发现一般形式的估计器存在如下的局限性：
- 对于一般形式的估计器 L_Est，估计器的无偏性将不可避免地导致无界方差和泛化误差界。
这说明，对于广义形式的估计器来说，无偏性和有界方差、泛化误差不可兼得。因此我们认为估计器设计的核心目标不仅仅是消除偏差、减少方差或仅仅实现偏差-方差的简单折衷，而是关于偏差和方差之间的定量联合优化，有必要开发一个动态估计框架来实现定量联合优化，动态估计器能够从用户-商品对的维度选择合适的估计器来实现最小化泛化误差的目的。
三、细粒度动态框架及估计器设计准则
基于 IPS 和基于 DR 的动态学习框架设计如下：
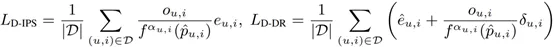
其中，f(∙) 为需要设计的函数，α_(u,i)∈[0,1] 为可优化的参数。当 f(p ̂_(u,i) )=p ̂_(u,i) 且 ∀α_(u,i)=1，D-IPS 和 D-DR 分别等价于原始的 IPS 和 DR 估计器，它们具有无偏性。当 f(p ̂_(u,i) )=p ̂_(u,i) 且 ∀α_(u,i)=0，D-IPS 和 D-DR 分别等价 |O|/D L_naive 和 EIB 方法，它们具有有界方差和泛化误差界。函数 f(p ̂_(u,i) ) 实际上是一个关于倾向性分数的映射，f(p ̂_(u,i) ) 的设计准则总结如下
- （保序性）f(p ̂_(u,i) )>p ̂_(u,i) 单调递增且满足 f(0)=0，f(1)=1。
- （同阶性）lim┬(p ̂_(u,i)→0)〖p ̂_(u,i)/f(p ̂_(u,i) ) 〗=C，其中 C>0 为正常数。
符合上述设计原则的一些具体函数表达式总结如下表所示。
D-IPS 和 D-DR 估计器的偏差和方差表达式如下所示：
偏差表达式：
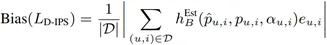
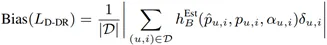
其中，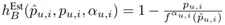
方差表达式：
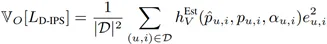
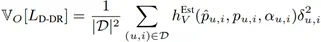
其中，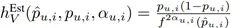
泛化误差界表达式：
其中，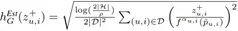
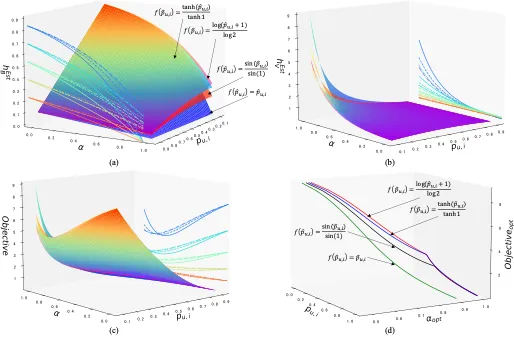
函数 h_B^Est 和 h_V^Est 分别决定了偏差和方差的大小，我们称函数 h_B^Est 和 h_V^Est 为偏差和方差的决定因子，函数 h_B^Est 和 h_V^Est 曲面如下图所示，可以看到，h_B^Est 随着 α_(u,i) 的增大单调递减；h_V^Est 随着 α_(u,i) 的增大单调递增。
四、偏差-方差定量联合优化
根据函数 h_B^Est 和 h_V^Est 的单调性，偏差-方差的折衷问题可以被定量形式化为如下的联合优化问题：
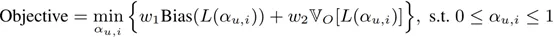
其中，w_1 和 w_2 为偏差和方差的权重。考虑到偏差和方差的决定因子，上述偏差-方差的联合优化问题可以被转换为如下所示的优化问题。
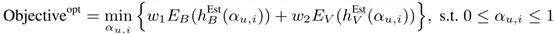
因为 f(p ̂_(u,i) ) 的设计准则，所以有 h_B^Est≥0 和 h_V^Est>0。因此，优化问题可以被进一步简化为：
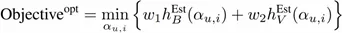
有了这一步的简化，我们就可以直接得到最优参数的解析解，最优参数的表达式如下所示：
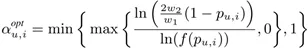
我们通过优化操作可以在不增加计算复杂度的基础上实现偏差和方差的定量优化，同时从理论层面保证方差和泛化误差的有界性。
方差和泛化误差有界性结论
- 如果动态估计器采用 α_(u,i)^opt 作为参数，则对应的方差和泛化误差是有界的。
五、实验结果
性能比较
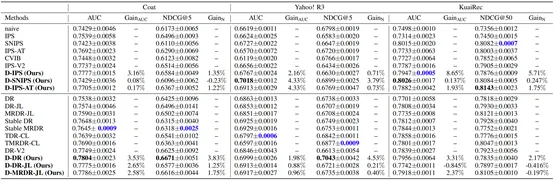
实验使用了三个具有 MNAR 和 MAR 样本的现实数据集，分别是 COAT，包含 290 名用户对 300 件外套的 4,640 个 MAR 和 6,960 个 MNAR 评分；YAHOO! R3，包含 15,400 名用户对 1,000 首歌曲的 54,000 个 MAR 和 311,704 个 MNAR 评分；以及 KUAIREC，包含 1,411 名用户对 3,327 个视频的 4,676,570 条观看比率记录。COAT 和 YAHOO! R3 中的评分分数在大于 3 时被二值化为 1，否则为 0。对于 KUAIREC 数据集，观看率在小于 2 时被二值化为 0，否则为 1。提出的动态估计器和 SOTA 方法的性能对比结果如下表所示。
消融实验
我们通过实验研究不同权重和函数对动态估计器的影响。我们给出了四个具体的函数表达式。我们将这四个动态估计器的权重设置为 w1=1 和 w2=[0.02, 0.04, 0.06, 0.08, 1]，以研究权重对性能和方差的影响。从最优参数方程可知，最优参数由权重比 w2/w1 决定。因此，我们只关注权重比对估计器性能和方差的影响，不同函数下，不同的权重比的模型性能由下图给出。
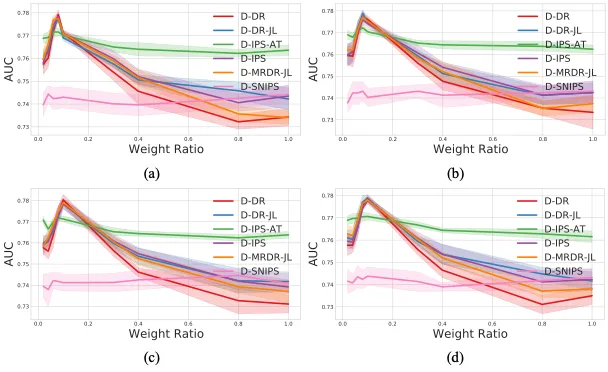
(a)p ̂_(u,i)^α; (b) (sin(p ̂_(u,i) )/sin2 )^α; (c) (log(p ̂_(u,i)+1)/log2 )^α; (d) (tanh(p ̂_(u,i) )/sin2 )^α
从上图可以看出，对于 D-IPS、D-IPS-AT、D-DR、D-DR-JL 和 D-MRDR-JL 方法，性能随着权重比的增加先增加后减小。同时，方差似乎在泛化性能达到最高值时达到最小值。由于权重比越小，动态估计器的偏差越小，上图中的实验结果表明，估计器的无偏性并不完全等价于模型性能。实际上，从给出的泛化误差表达式来看，偏差-方差联合优化可以最小化估计器的泛化误差界，从而进一步提高模型的泛化性能。对于 SNIPS，方差减少的特性可能会导致非直观的性能和方差趋势。
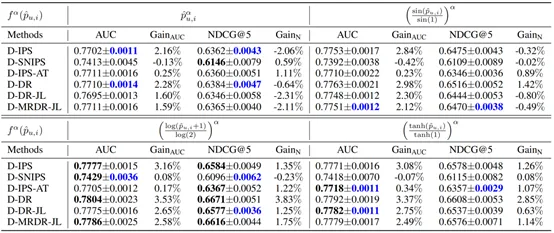
在相同的权重比 w2/w1=0.1 下，我们进一步讨论不同函数对模型性能和方差的效果。从下表可以看出几乎所有具有不同函数表达式的动态估计器性能都优于相应的原始纠偏方法。这进一步证明了所提出的动态学习机制可以极大地提高原始估计器的性能。
六、结语
据我们所知，这是第一个揭示估计器设计本质的工作。该工作指出，估计器设计的本质不仅仅是消除偏差、降低方差或实现简单的偏差-方差权衡，而是同时定量优化偏差和方差。此外，该工作还阐述了通用正则化技术和静态估计器的局限性。基于偏差和方差之间关系的一般规律，我们提出了一种系统的动态学习框架，通过细粒度的偏差-方差联合优化方案，保证了方差和泛化误差界的有界性。大量的实验结果验证了该工作的理论结果和当前动态估计器的性能。在动态估计框架中，对目标函数中权重的搜索以及函数的搜索仍然是一个开放问题，值得进一步探索。
