本篇工作已被 NeurIPS(Conference on Neural Information Processing Systems)2024 会议接收,并被评为 Oral Presentation (72/4553) 。该文章的第一作者陈麒光,目前就读于哈工大赛尔实验室。他的主要研究方向包括大模型思维链、跨语言大模型等。
该研究主要提出了推理边界框架(Reasoning Boundary Framework, RBF),首次尝试量化并优化思维链推理能力。

- 论文链接:https://arxiv.org/abs/2410.05695
- 代码地址:https://github.com/LightChen233/reasoning-boundary
1. 大型语言模型(LLMs)与思维链推理能力
什么是思维链(Chain-of-Thought, CoT)?
近年来,大型语言模型(LLMs) 在处理各种复杂任务中取得了长足进展,从文本生成到问题解答,LLMs 几乎无所不能。然而,面对复杂的推理任务,LLMs 也存在瓶颈 —— 模型往往容易跳过推理的中间步骤,直接生成最终答案,这使得它们在应对复杂问题时容易犯错。
思维链推理(CoT) 是一种让模型分步推理复杂问题的方法。与传统模型的直接生成答案不同,CoT 通过逐步细化问题的每一步,从而得到更准确、更有逻辑的结果。
为什么它如此重要?
为什么 CoT 很重要?因为面对复杂的推理任务,模型往往会因为信息量大、推理路径复杂而犯错。CoT 的逐步推理策略使模型能够处理更具挑战性的任务 —— 从数学题解到现实决策问题,它能帮助模型分解任务,找到每个步骤的最佳解法。
这不仅提升了模型的准确性,还显著增强了它处理复杂任务的能力,使其能够应用于更广泛的实际场景中。
2. 模型推理的困境:复杂任务中的可解释性难题
想象这样一个情景 :你正在处理一个复杂的项目,需要模型综合多种能力,最终通过多步推理找到最优解决方案,那么这些能力和推理能力是如何组合,共同影响并改进最终性能的呢?
为了解决该问题,该文章通过研究以下几个问题来理解和解决这个问题。
2.1 模型在面对复杂推理时,如何对推理能力进行量化?
当前多数研究依赖定性分析,缺乏统一的量化指标来系统比较不同的 CoT 推理方法。这种局限性导致研究者难以精确评估和预测模型在复杂任务中的推理能力上限,阻碍了对 CoT 推理效果的深入理解和科学验证。
为此,研究人员提出推理边界框架(Reasoning Boundary Framework, RBF),定义了模型在不同准确率对于的推理能力边界。并提出了三种推理边界以量化推理能力边界:完全可行推理边界(CFRB);完全不可行推理边界(CIRB); 部分可行推理边界(PFRB)。
2.2 推理能力与不同的其他能力如何组合?
在实际场景中,模型往往需要集成多种能力才能有效地解决某一任务。
为了定量描述如何通过思维链 CoT 机制实现多种能力的协同提升,研究者进一步提出了 “ 推理边界的组合律 ”,并推导并验证了该组合律的具体公式。
2.3 如何基于可解释性框架优化思维链?
虽然已有研究揭示了 CoT 推理的部分机制,但如何系统性地优化 CoT 推理的效率和效果仍缺少明确的策略与方法指导。这一不足限制了 CoT 技术在实际应用中的进一步改进与拓展。
根据推理边界框架,本文提出了最短可接受推理路径(MARP) 优化推理效率。无论是在复杂的数学推理还是多跳推理中,RBF 都能帮助模型在海量信息中找到最优路径,大幅提升推理效果。
3. 概念定义
3.1 推理边界
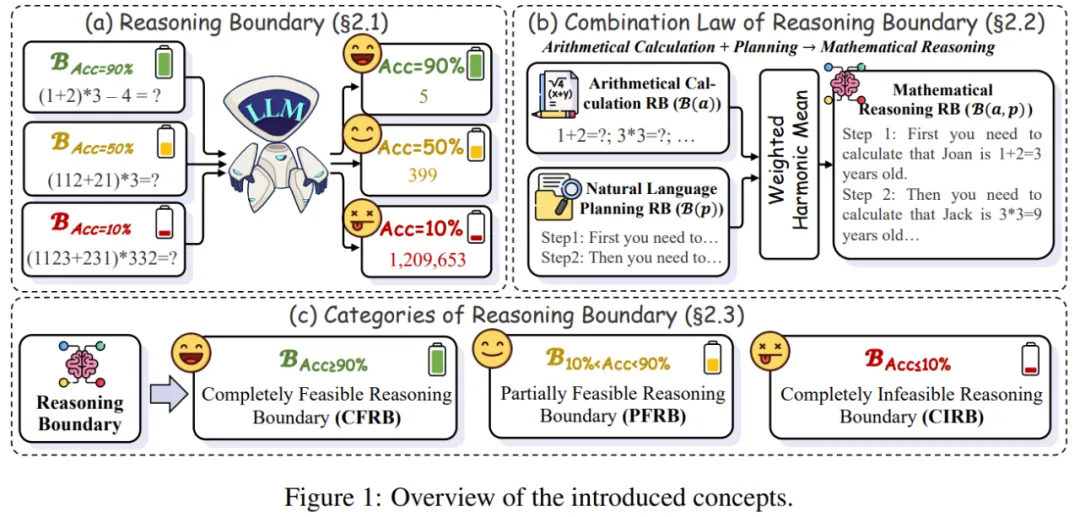
为了量化大型语言模型的复杂推理能力,如图 1 (a) 所示,研究者引入了推理边界(Reasoning Boundary, RB) 的概念,定义了 LLMs 在特定推理过程中能够处理的任务难度上限。
具体而言,RB 被定义为模型 m 和任务 t 作为问题难度 d 的最大值,模型的准确性达到预定义阈值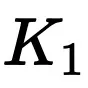 :
:
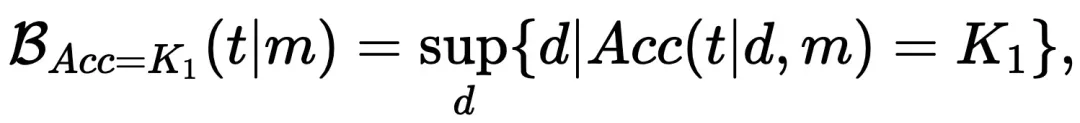
其中 Acc (t|d, m) 表示模型在难度为 d 的任务 t 上的准确率。难度可以通过推理步骤数或计算复杂度等因素来衡量。简而言之,RB 反映了模型在保持一定准确性(accuracy)的前提下,其推理能力的边界。
* 为了简洁起见,在后续文章中将 RB 表示为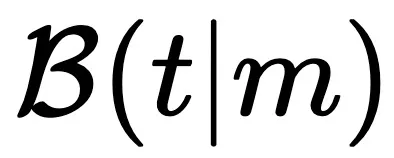 。
。
总结:模型的推理边界是由其针对给定任务难度实现特定准确度的能力来定义的。
3.2 推理边界间的组合律
在实际场景中,模型往往需要集成多种能力才能有效地解决某一任务。
为了定量描述如何通过思维链 CoT 机制实现多种能力的协同提升,研究者提出了“推理边界的组合律”,并推导出 CoT 能力上限的具体公式。
该定律估计模型 m 内 n 个任务的统一推理边界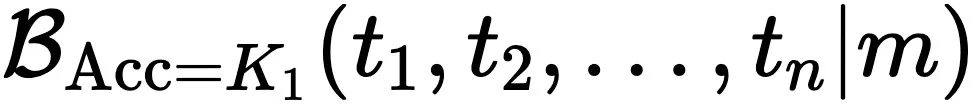 ,即表述为:
,即表述为:
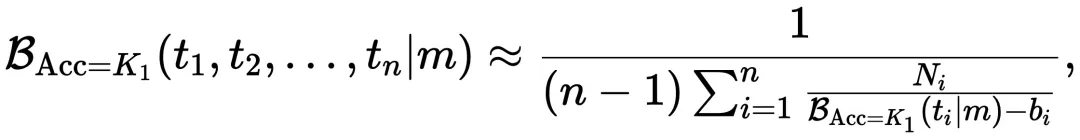
其中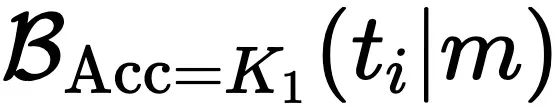 表示任务
表示任务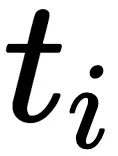 的推理边界。
的推理边界。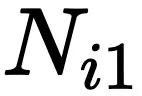 和
和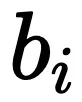 是缩放因子,仅受相关任务影响。如图 1 (b) 所示,该方程提供了一个数学公式来估计独立 RB 的组合,从而可以更深入地了解复杂任务的模型行为。
是缩放因子,仅受相关任务影响。如图 1 (b) 所示,该方程提供了一个数学公式来估计独立 RB 的组合,从而可以更深入地了解复杂任务的模型行为。
总结:推理边界的组合律描述了多个推理能力的协同效应,满足加权调和平均公式,用以估计模型在多个任务上的整体推理能力。
3.3 推理边界划分
此外,为了指导 CoT 的优化和更方便的表达,如图 1 (c) 所示,研究者根据经验准确性定义了以下三类 RB:
- 完全可行的推理边界:研究者定义准确率大于 90% 的部分是完全可行的推理边界 (CFRB=
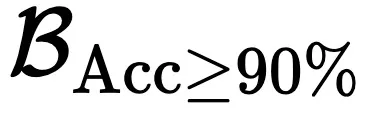 ),这意味着 LLM 可以有效地掌握这部分的表现。
),这意味着 LLM 可以有效地掌握这部分的表现。 - 完全不可行的推理边界:研究者认为准确率小于 10% 的部分是完全不可行的推理边界 (CIRB=
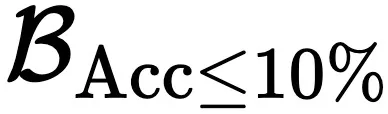 ),这意味着模型永远无法有效掌握这部分的性能。
),这意味着模型永远无法有效掌握这部分的性能。 - 部分可行推理边界:研究者将除 CFRB 和 CIRB 之外的其余部分中的 RB 定义为部分可行推理边界 (PFRB=
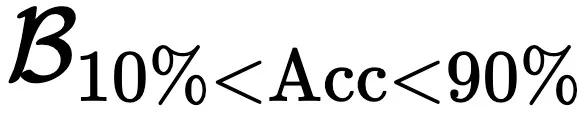 ),这需要模型重复思考或者更清晰的信息来解决问题。
),这需要模型重复思考或者更清晰的信息来解决问题。
研究者通过详细分析了这三类 RB 的性质,进一步结合组合律来优化这三个推理边界,从而为支持未来 CoT 优化提供有效的建议和指导。
4. 实验设置
- 模型设置:研究者们采用了 GPT-3.5-Turbo 作为主要模型,实验还涵盖了多任务场景,包括数学推理、多跳问答和多语言推理等领域,以确保推理边界的全面评估。
- 基准设置:为了更好地评估 LLMs 的推理能力,作者引入了一个新的数据集 ——BigGSM。这个数据集不仅具有较高的计算复杂性,还包含更长的推理链,能够更好地挑战模型的推理上限。
5. 验证性实验
5.1 推理边界存在性验证
研究者们通过实证分析,验证了推理边界在三类任务中的普遍性:
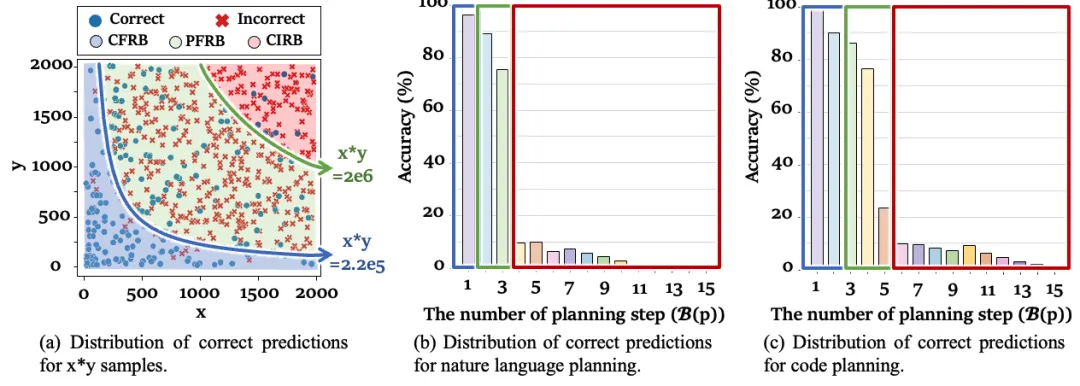
在基础算术运算中,呈现出三种不同的推理边界 (图 2 (a));
在自然语言规划任务中,同样展现出三种不同的推理边界 (图 2 (b));
在代码规划任务中,仍然表现出一致的三种推理边界 (图 2 (c))。
5.2 推理边界组合律验证
在实际应用中,模型通常需要集成多种能力才能高效解决复杂任务。为此,研究者们进一步地验证了实际场景中,推理边界组合律的广泛适用性:
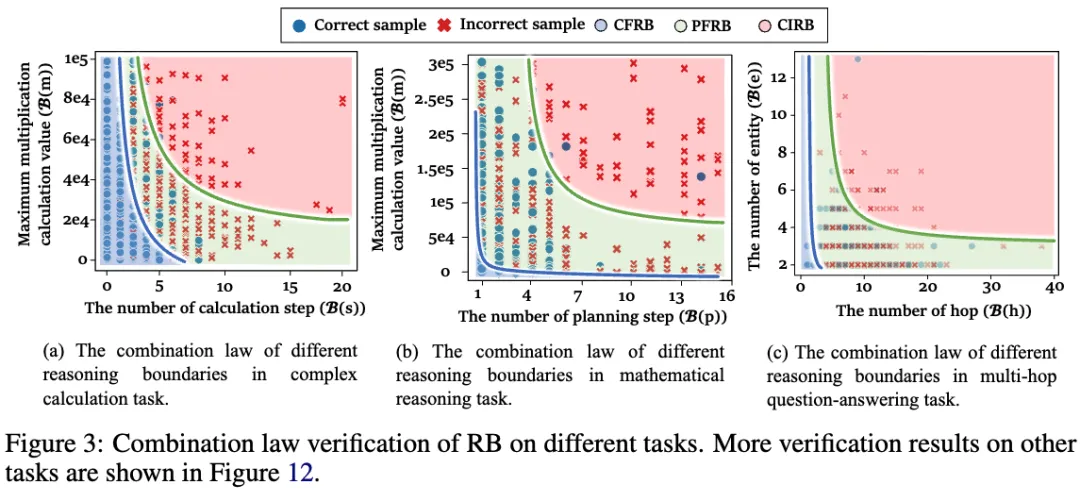
- 复杂多项式计算的推理边界:可视为 ①计算步骤规划 与 ②数学运算 两个推理边界的结合。如图 3 (a) 所示,实验结果显示了三个具有明显边界的推理边界划分区域。
- 复杂小学数学推理的推理边界:可理解为 ①自然语言步骤规划 与 ②数学运算 的结合,图 3 (b) 中同样展示了三个清晰的推理边界划分区域。
- 多跳问答的推理边界:可被视作 ①多跳规划 与 ②实体推理 的结合。正如图 3 (c) 所示,三个推理边界划分的有效区域同样可见。
5.3 不同推理边界的不同性质
研究者验证了不同推理边界在模型中的性质:
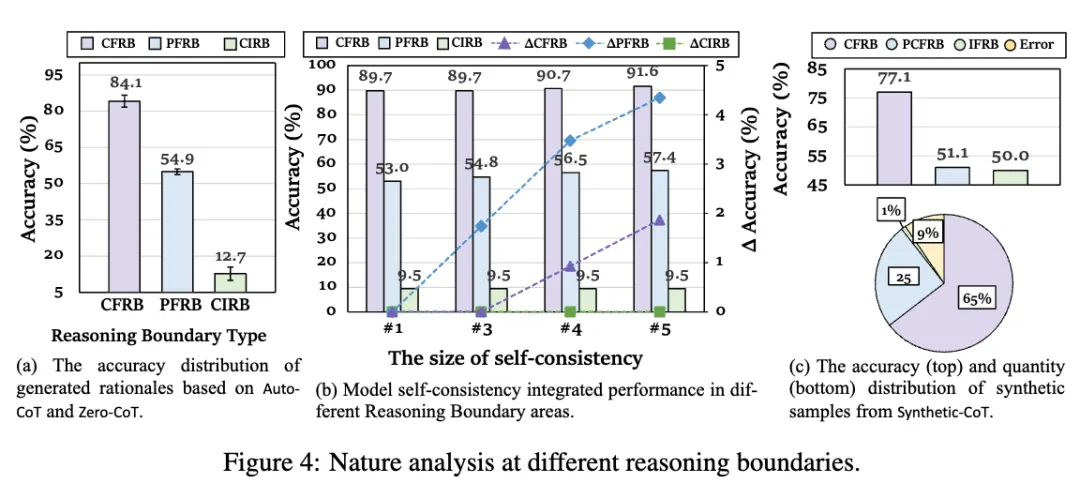
- 完全可行推理边界-->完全掌握:如图 4 (a, b) 所示,在这一边界下,模型即使在没有示例、无需 self-consistency 的情况下也能够高效完成任务。
- 部分可行推理边界-->不完全掌握:在这一推理边界下,如图 4 (b) 所示,模型对任务的掌握程度有限,需要通过多次 Self-consistency 来增强信心,从而提高准确率。
- 完全不可行推理边界-->完全不掌握:在这种边界下,如图 4 (b) 所示,模型的推理表现极其有限,即便采用 Self-consistency,模型的准确率仍难以得到提升。
- 大模型能够自己意识到自己的推理边界:研究还发现,如图 4 (c) 所示,当让模型自行生成 CoT 示例时,模型更倾向于生成符合其推理边界的样本,特别是在完全可行推理边界范围内,而很少生成其完全无法掌握的样本。这表明模型对推理边界具有一定的自我感知能力,能够根据自身能力选择合适的任务进行推理。
6. 基于推理边界的 CoT 优化
为了进一步优化思维链的表现,研究者们提出了基于推理边界优化的多种策略,并对这些策略进行了全面的实验验证,揭示了如何通过调整 RB 提升复杂任务中的推理能力。
6.1 推理边界优化策略
工具使用可以提升大语言模型的推理边界
当模型使用工具时,可以简单地认为模型可以以无限精度执行计算,因此数学计算的推理边界趋向于无穷大,即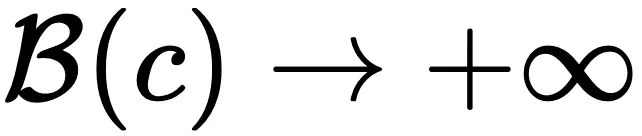 。显然,模型的组合推理边界可以计算为:
。显然,模型的组合推理边界可以计算为:
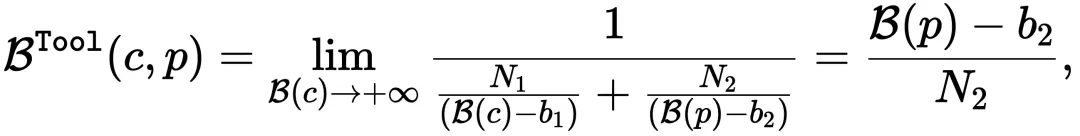
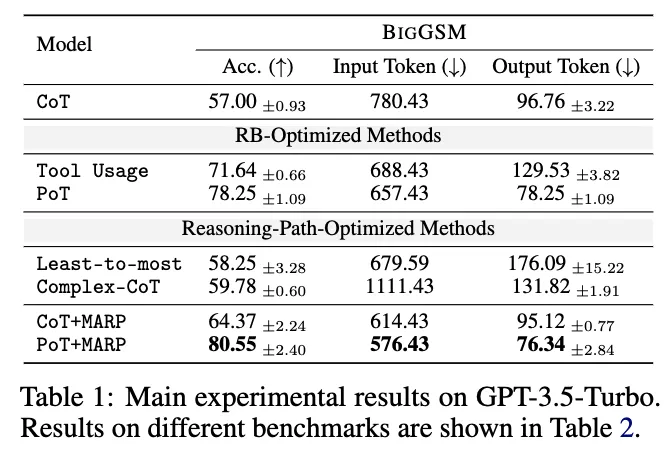
其中,c 表示计算任务,p 表示规划任务。很容易得出,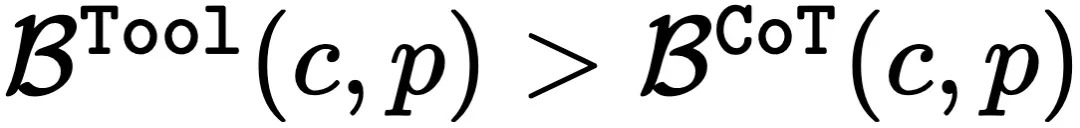 ,这表明工具使用可以提高推理的边界。这解释了为什么工具使用比普通的推理链性能更好(见表 1)。此外,如图 5 所示,理论推理边界与实际推理边界的分布几乎完美重合,这也证明了该假设的可靠性和适用性。
,这表明工具使用可以提高推理的边界。这解释了为什么工具使用比普通的推理链性能更好(见表 1)。此外,如图 5 所示,理论推理边界与实际推理边界的分布几乎完美重合,这也证明了该假设的可靠性和适用性。
程序化思维可以进一步提升大语言模型的推理边界。
由工具使用的组合推理边界计算公式可得,LLM 的推理边界完全取决于其规划能力。由于自然语言可能过于冗长,它会妨碍 LLM 的规划能力。因此,程序化思维(Program-of-Thought,PoT)通过代码提供了更清晰的逻辑表示,使得规划更为清晰(如图 2 (b, c) 所示)。所以,这导致更好的步骤规划推理边界,即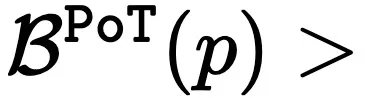
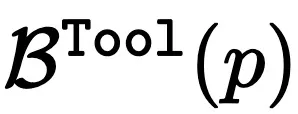 。那么,PoT 的推理边界
。那么,PoT 的推理边界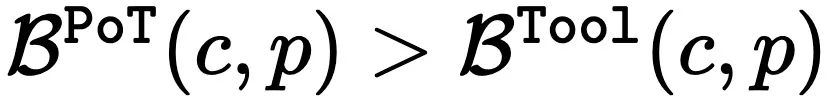 。
。
6.2 推理路径优化策略
对于固定推理方式的模型而言,其推理边界(即能力边界)是相对固定的。因此,关键问题在于如何通过优化策略,提升模型的推理能力,使得优化后的推理边界超越原问题所需的边界。
- Complex CoT 在推理步骤与性能之间的平衡
- 单次计算负荷缓解:研究表明,通过增加推理步骤,可以缓解单次计算的负荷,从而提升模型的计算边界
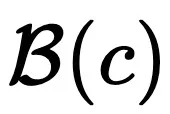 ,这有助于提高整体的推理能力。
,这有助于提高整体的推理能力。 - 规划难度增加:然而,推理步骤的过度增加可能带来负面影响:原问题在准确率较高的边界
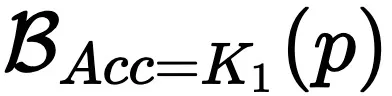 上,经过 Complex CoT,可能落到准确率较低的边界
上,经过 Complex CoT,可能落到准确率较低的边界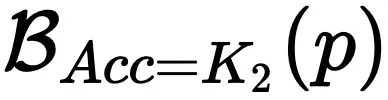 上,其中
上,其中 。这意味着过多的推理步骤可能导致组合推理准确度的下降。
。这意味着过多的推理步骤可能导致组合推理准确度的下降。
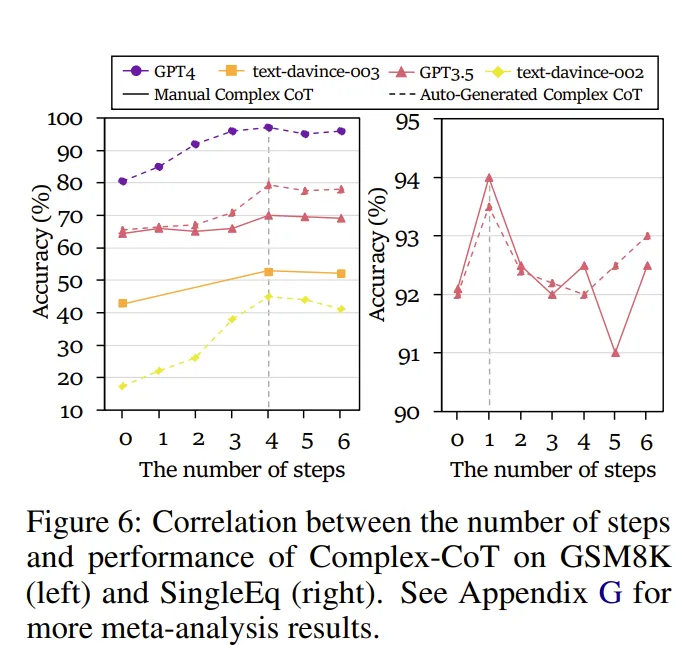
- 在规划与计算负荷之间存在一个平衡:如图 6 所示,随着推理步骤的增加,模型性能在初期显著提高,但当步骤数超过模型的最优推理能力时,性能开始下降。这表明,Complex CoT 在推理步骤数量与计算负荷之间存在一个最佳平衡点。超出这一点,计算负荷的增加会对模型的整体表现产生负面影响。
- Least-to-Most 的分步优化策略
局部规划压力缓解:通过将问题拆解为多个子问题,如图 7 所示,可以有效减少每个步骤内的规划压力,对各种不同计算量的问题都能有一定的性能提升。
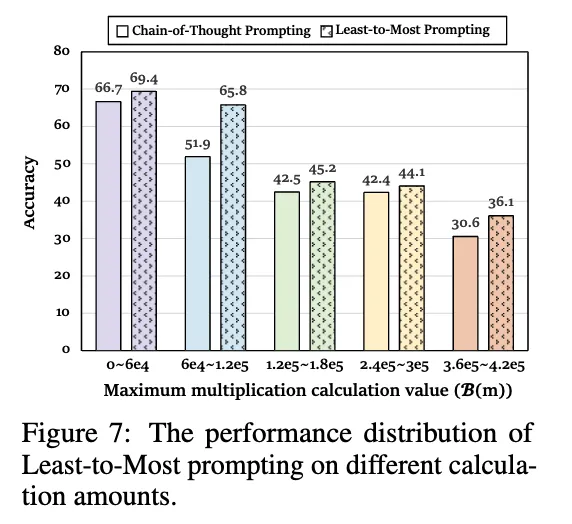
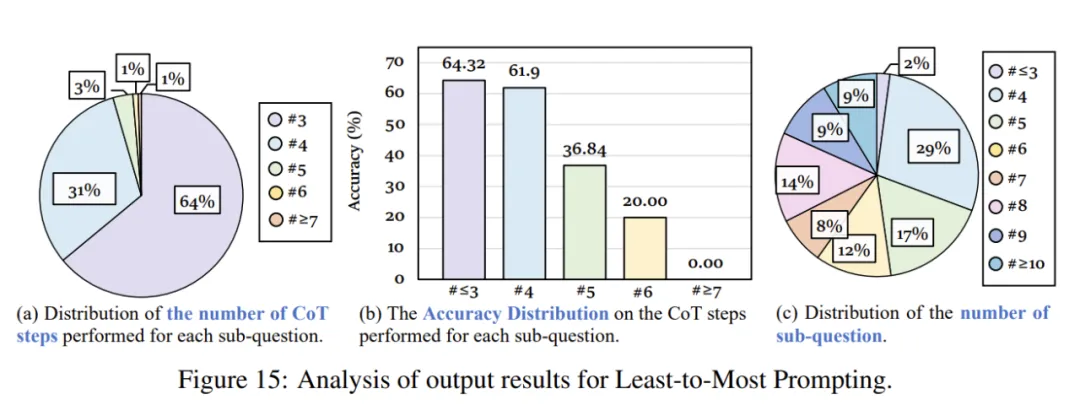
全局规划难度增加:虽然这种策略能够降低局部规划负担,它同时引入了全局分解规划中的额外推理边界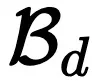 。如图 15 所示,接近 70% 的全局规划数超过了 5 步,严重加大了模型规划难度,从而使实际的组合推理边界对应的准确率下降。
。如图 15 所示,接近 70% 的全局规划数超过了 5 步,严重加大了模型规划难度,从而使实际的组合推理边界对应的准确率下降。
- 最短可接受推理路径提示(MARP)
为了克服上述策略的局限性,研究者提出了最短可接受推理路径提示(MARP)策略。该策略通过提示大模型在每个步骤中尽可能高效地执行计算,同时减少不必要的全局规划,从而降低了模型的计算负担和规划复杂度:
- 最小化推理路径提示:为了减轻与规划相关的认知负担,通过该提示让模型尽可能简洁地回答问题,确保提供简短、清晰和直接的推理路径。
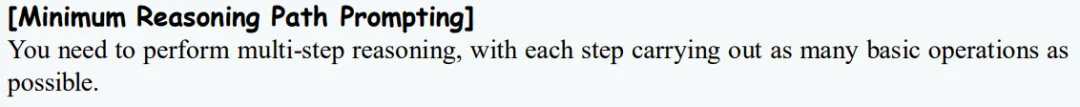
- 可接受推理路径提示:为了更有效地利用推理边界的上限,通过该提示要求模型每一个推理步骤的复杂性在可接受的范围内。

实验结果(见表 1)显示,MARP 显著提高了模型性能,并有效减少了 token 的使用量。
7. 拓展性探索
7.1 模型扩展验证
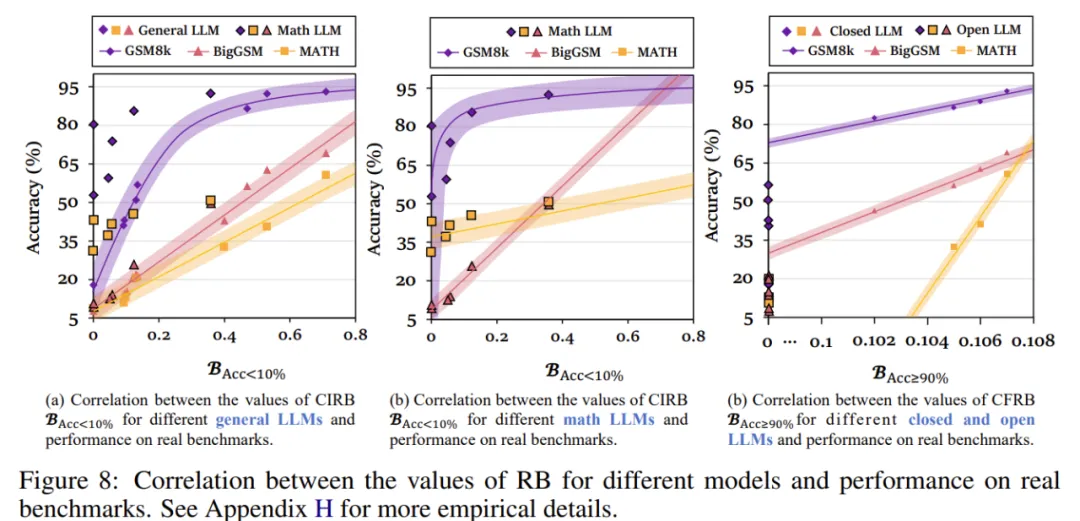
- 推理边界与模型准确率的正相关性:研究者通过对 25 个不同模型的推理边界表现进行分析,发现推理边界与数学任务中的准确率呈现出正相关关系。
- 数学模型与通用模型在推理边界 - 准确率分布上的差异:通过数学数据微调的模型,推理边界 - 准确率分布虽然呈现出正相关,但与通用 LLM 存在显著差异。这可以为未来区分模型是否进行了数学专项训练提供了一个潜在的指标。
- 开源模型在完全可行推理边界上的局限性:开源模型在完全可行推理边界(CFRB)上的表现与闭源模型存在显著差异。几乎所有开源模型的 CFRB 值均为 0,这表明开源模型在高级推理任务上的不足,表明其在未来优化中的潜力。
7.2 任务扩展验证
更进一步地,该研究不仅验证了在数学运算、数学推理和多跳问答任务中的推理边界扩展规律,还进一步探索了在多语言推理和医疗推理任务中的表现。
- 多语言推理:通过将多语言能力、数学计算与推理规划相结合,实验结果表明,这些能力的正交组合后,推理边界依然保持了三类不同的推理边界模式,进一步证实了此方法的普适性和稳定性。
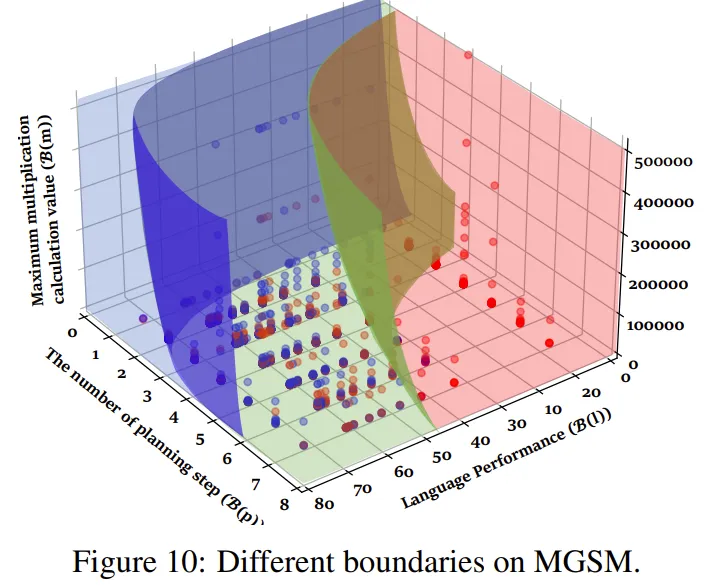
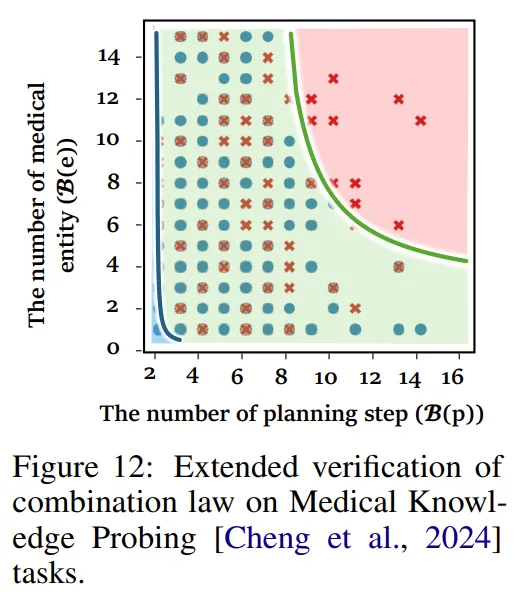
- 医疗推理:类似地,在医疗领域,研究通过将医疗实体推理与多跳推理规划相结合,验证了推理边界在正交组合后仍然保持一致,说明该推理策略同样适用于医疗推理任务。
8. 如何理解 o1 的优异性能?
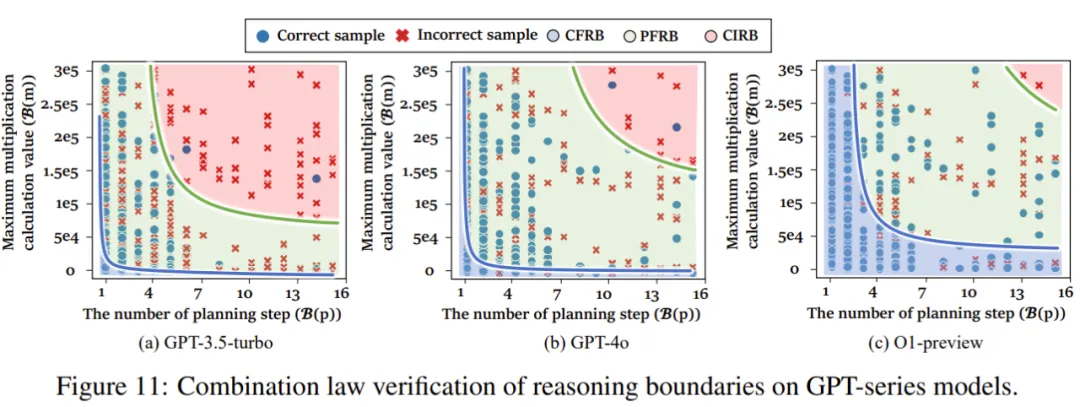
为了深入理解当前最先进的大型语言模型 o1,研究人员利用推理边界框架对 GPT 系列模型进行了全面评估。
如图 11 所示,与早期版本相比,各项推理边界指标均有显著提升,模型性能也随之增强。特别是,尽管 GPT-3.5 与 GPT-4o 之间在 完全不可行推理边界(CIRB) 上的改进幅度较大,但 完全可行推理边界(CFRB) 的提升相对较小。然而,在 GPT-o1 版本中,完全可行推理边界的表现则有了显著改善。
进一步来看,图 14 揭示了 GPT-o1 版本在完全可行推理边界上的卓越表现,提升幅度几乎是其他模型的三倍。
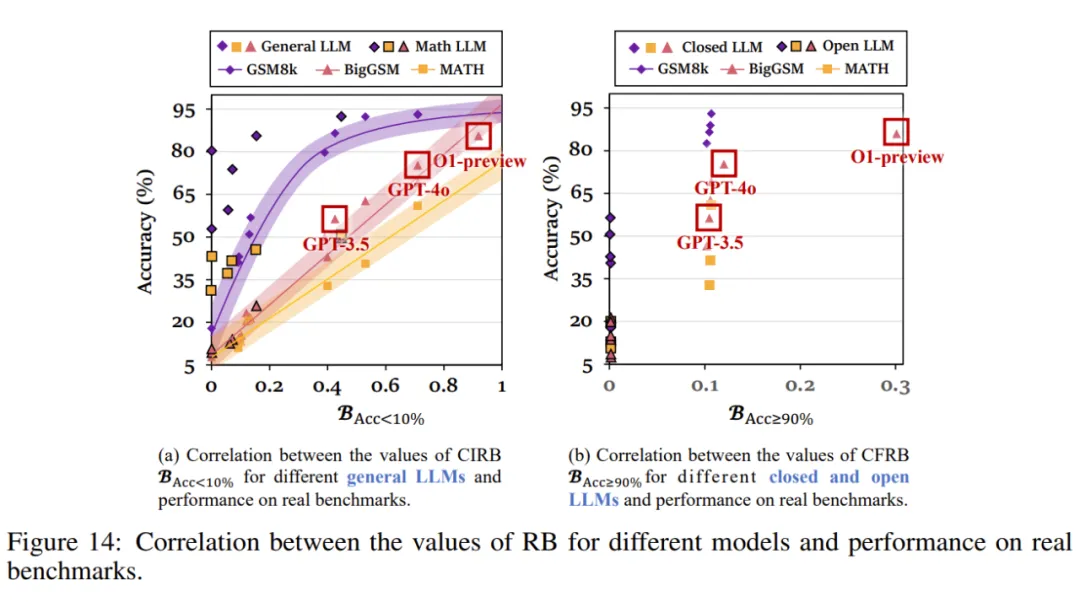
研究人员认为,这一成果主要归功于逻辑强化学习技术的进步和 Inference Scaling Law 策略的优化。这些新策略在提升完全可行推理边界方面起到了关键作用,远远超越了常规的改进路径。这一现象可能为未来研究提供了新的方向和启示。
总结
本研究提出了一个推理边界(RB)框架,系统量化并优化大语言模型(LLMs)在思维链(CoT)任务中的推理能力边界。通过定义推理边界和应用优化策略,合理解释了多个 CoT 策略其在推理性能上的优势。同时,最短可接受推理路径(MARP)策略通过减少不必要的推理步骤,显著提高了不同任务中的推理性能与效率。研究者希望 RB 框架能够为相关研究提供理论基础,推动 LLMs 在复杂推理任务中的发展。











































