消除激活值(outliers)，大语言模型低比特量化有新招了——
自动化所、清华、港城大团队最近有一篇论文入选了NeurIPS 2024（Oral Presentation），他们针对LLM权重激活量化提出了两种正交变换，有效降低了outliers现象，达到了4-bit的新SOTA。
简单理解，在大语言模型（LLM）中，有一些中间层输出的数值（激活值 Activation）会变得非常大，它们被称为“outliers（离群值）”，这些 outliers给模型量化带来了挑战。
补充一下，量化可以将模型中的数值从浮点数转换为整数，以减少模型的大小和计算需求。
而一旦在量化过程中存在大量outliers，会导致量化后的模型性能下降。
明白了这层道理, 我们再来看他们团队的一项名为DuQuant的新研究。
首先, 他们发现在LLM的前馈网络 (FFN) 模块中的down_proj层, 存在明显的Massive Outliers(非常大的激活值)。
这种outliers不同于以往发现的Normal Outliers，表现为大于绝对值几百的异常值并局限于个别的tokens中——
它们导致现有的量化算法（如SmoothQuant和OmniQuant）在将模型的权重和激活值量化为4位二进制数时表现不佳。
对此，团队提出了一种新的量化方法，叫做DuQuant。
DuQuant通过学习旋转和置换变换矩阵，在Activation矩阵内部将outliers转移到其他通道，最终得到平滑的激活矩阵，从而大幅降低了量化难度。
实验显示，使用DuQuant方法，在4位权重和激活量化的设置下，模型达到了SOTA。
同时，DuQuant的训练非常快速，可以在50s内完成7B模型的量化过程，即插即用。
背景
在每个Transformer块的常见模块中，多头自注意力（MSA）和前馈网络（FFN）基本上都由线性层组成，将其表示为：
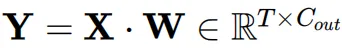
其中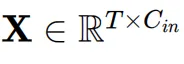
是激活输入，
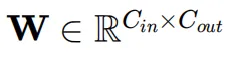表示权重矩阵。
模型量化通过将浮点数（FP16, BF16）表示的模型权重或激活值转换为低位的浮点数或整数来减少内存占用，权重激活量化可以通过使用低比特乘法的算子进一步加快模型推理的速度。
该工作重点关注低比特整型量化，目标是获得更好的硬件支持。
具体来说， 𝖻位量化过程将FP16张量𝐗映射为低位整数𝐗𝗊 ：
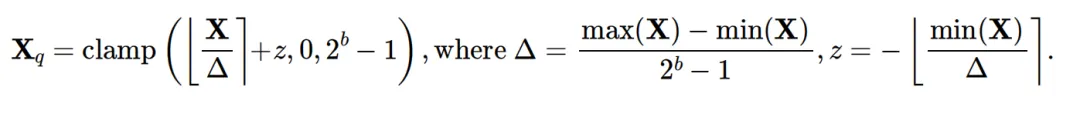
符号⎣ · ⎤表示最接近的舍入操作， ∆是量化步长， 𝑧表示零点。
遵循主流量化方法，作者对激活𝐗采用逐token量化，对权重𝐖采用逐通道量化，这意味着为𝐗的每个token分配不同的步长（ ∆𝐗 ∊ ℝ𝑻x1），为𝐖的每个输出通道分配不同的步长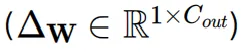
。
动机（Motivation）
据作者介绍，他们首次在实验中发现，LLM FFN模块中的down_proj layer存在明显的Massive Outliers（非常大的激活值），表现为绝对值大于几百的异常值并局限于个别的token中。
PS：先前工作发现Massive Outliers存在于每个transformer block的输出中，DuQuant的作者进一步将其定位在FFN模块中。
论文：https://link.zhihu.com/?target=https%3A//eric-mingjie.github.io/massive-activations/index.html
这些Massive Outliers造成SmoothQuant和OmniQuant等算法在4bit WA量化中表现较差。
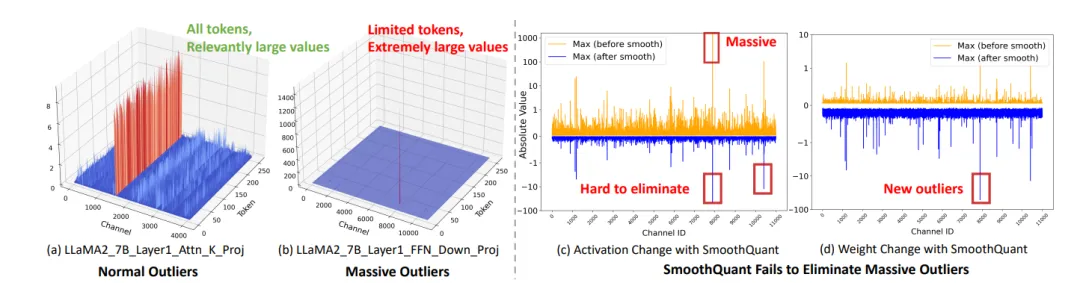△图1：Massive outliers显著加大了低比特权重激活量化的难度
图1(a)(b)对比了普遍常见的Normal Outliers，和在FFN中出现的Massive Outliers。
SmoothQuant通过将激活值除以每通道平滑因子并将其乘回权重矩阵，尝试将量化难度从激活值转移到权重。
具体来说，SmoothQuant使用逐通道的平滑对角矩阵，记为𝞚 ，将原始线性层重新表达为：𝐘=𝐗 · 𝐖=（𝐗 ·𝞚）（𝞚-1 · 𝐖），对角矩阵𝞚中的元素𝞚𝑗 的计算方式为：
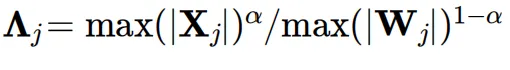
其中α是一个超参数，表示迁移强度。
然而，作者观察到在输入端进行这种转移可能会导致权重矩阵也出现明显的难以量化的outliers（如图1(d)所示），这一问题的根源在于Massive Outliers使平滑因子𝞚𝑗 变得异常大。
此外，极大的outliers还可能导致基于优化的方法出现梯度爆炸的问题，所以基于梯度优化的OmniQuant和AffineQuant等工作会直接跳过down_proj layer，直接退化为SmoothQuant的处理方式。
这些preliminary experiments都表明需要一种更新更好的方式处理两种outliers，特别是平滑掉down_proj输入侧的Massive Outliers。
方法
DuQuant提出通过学习旋转和置换变换矩阵，在Activation矩阵内部将outliers转移到其他通道，最终得到平滑的激活矩阵，从而大幅度降低了量化难度。
(a) 逐步展示了DuQuant算法对Normal outlier的处理过程，(b) DuQuant显著降低了Massive outlier，(c）一个Tony Example说明DuQuant有效降低了激活矩阵的量化难度。
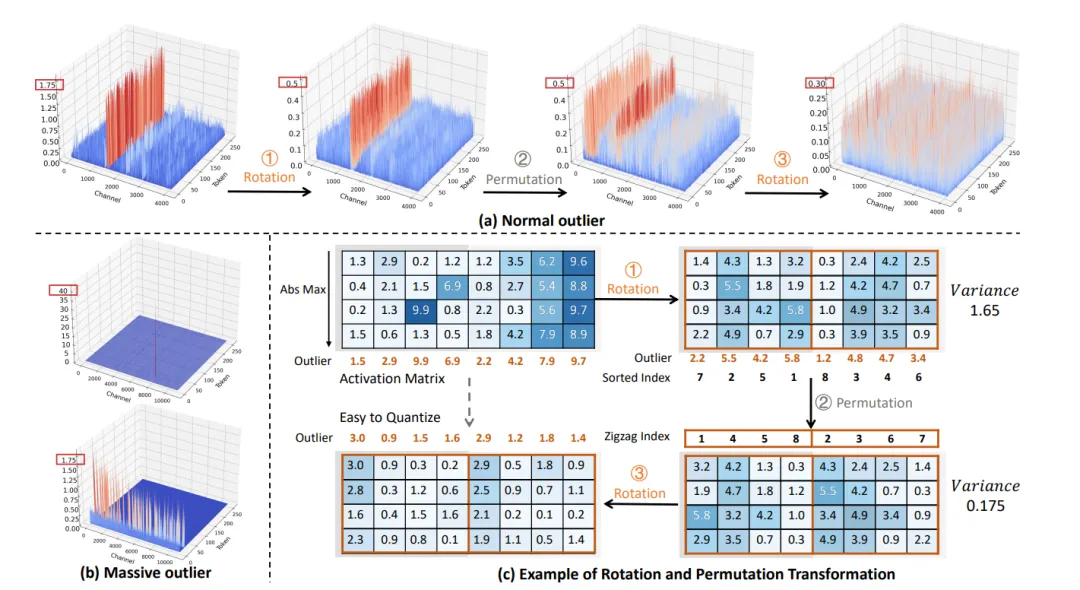△图2：DuQuant算法说明
简单来说，DuQuant算法包含三个步骤：
1）旋转矩阵的构造有效利用了特定outlier channel的位置索引，作者使用了分块对角的旋转矩阵，在每个block内部通过贪心算法将outlier平摊到其他的channels中。
2）由于block size的限制，可能导致某些block在旋转之后组内的平均值大于其他blocks，因此作者进一步使用通道置换技术重新分配activation channel，使用zigzag顺序排列使各组均值的方差大幅减小。
3） 进一步执行一次旋转变换达到更均匀的activation分布，从而大幅降低了量化难度。
旋转矩阵：作者希望应用旋转矩阵𝐑进行行或列变换，减轻Normal Outliers和Massive Outliers的影响。
由于Massive Outliers通常随机分布在激活空间中，直接找到能够通过单次旋转变换减轻outliers的最优旋转矩阵𝐑是具有挑战性的。
为了解决这一问题，作者采用带有先验知识的贪心搜索方法来计算旋转矩阵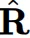
，从而近似理想的旋转矩阵𝐑。
具体来说，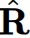
的计算包括以下步骤：
1、识别outliers主要集中的特征维度 ，即：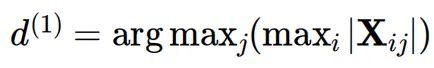
，其中， 𝐗𝑖𝑗表示𝐗中第𝑖行和第𝑗列的元素。
2、基于搜索到的维度，构建旋转矩阵如下：
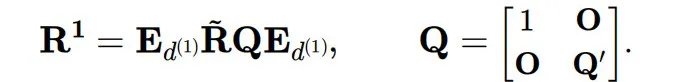
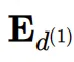是用于交换激活值的第1列和第d(1) 列的交换矩阵，表示一个正交初始化的旋转矩阵，其第一行均匀分布。
这样做的目的是通过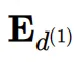
变换后减轻第1列中的outliers。
为了进一步增加随机性，保留减轻outliers后的第1列，并通过与随机正交矩阵𝐐’相乘，随机旋转其他列。
3、设N为贪心搜索的步数，则近似的旋转矩阵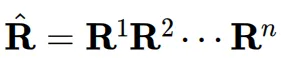
，其中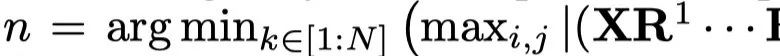
。每个𝐑𝑖 根据公式(2)和识别到的特征维度d(𝑖) 构建。
通过这种构建方式，可以确保近似的最优旋转矩阵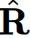
能够有效减轻具有较大幅度的outliers，而不仅仅是使用随机选择的正交旋转矩阵。
然而，直接构建整个旋转矩阵非常耗时，并且会导致大量的内存开销。
为了实现快速矩阵乘法，参考Training Transformer with 4ibts ，作者选择以分块的方式近似旋转矩阵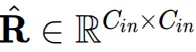
。
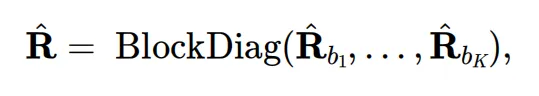
其中，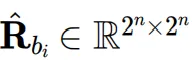
表示第𝑖个块的方阵，该矩阵按照上述三步构建。块的数量K通过K=C𝑖n/2n计算得出。
通道置换矩阵：尽管采用了块对角旋转矩阵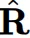
来提高时间和存储效率，但其专注于局部信息的特性带来了进一步减少outliers的潜在限制。
由于在每个小块内进行的旋转变换无法整合跨不同块的信息，一个块中可能有相对较大的outliers，而另一个块中则有较小的outliers，导致不同块之间存在较高的方差。
因此，作者提出利用通道置换矩阵平衡不同blocks之间outliers的幅度。
具体来说，在每个小块中，将维度d𝑗中最大的outlier记为O𝑗。
同时， Mb𝑖表示第𝑖个块中所有O𝑗的平均值，其中𝑖=1，2，……，K ，各个块之间激活幅度的方差可以表示为：
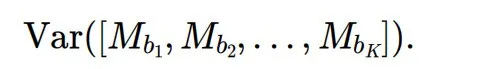
作者引入了之字形置换矩阵P 。
具体来说，通过生成一个之字形序列，首先将激活值最高的通道分配给第一个块，接着，将激活值次高的通道按递减顺序分配到后续的块，直到第K个块。
在到达最后一个块后，顺序反转，从下一个激活值最高的通道开始，按递增顺序分配。
这个往复模式贯穿所有块，确保没有单个块持续接收最高或最低激活值的通道。
通过使用之字形置换，DuQuant实现了不同块之间outliers的均衡分布，从而能够使用额外的旋转变换进一步平滑outliers，如图2所示。
需要注意的是：
1、通道置换其实是非常重要的一步，也很简单快速（对于推理效率的影响很小，可见后面实验部分），既可以避免像SpinQuant那样复杂的训练流程，也比QuaRot的Hadamard旋转性能表现更好。
2、旋转矩阵和置换变换矩阵都是正交矩阵，保证了𝐗𝐖输出的不变性，作者还通过严谨的理论推导了证明了两种变换有效降低了量化误差，具体证明可以阅读Paper里面的Appendix。
实验
在4-bit setting下达到了SOTA的效果，DuQuant验证了LLaMA、Vicuna、Mistral系列模型，在PPL、QA、MMLU和MT-Bench等任务上都明显提升了量化模型的性能。
此外作者还在LongBench评测了量化模型长文本生成的能力，DuQuant同样大幅超过了baselines。
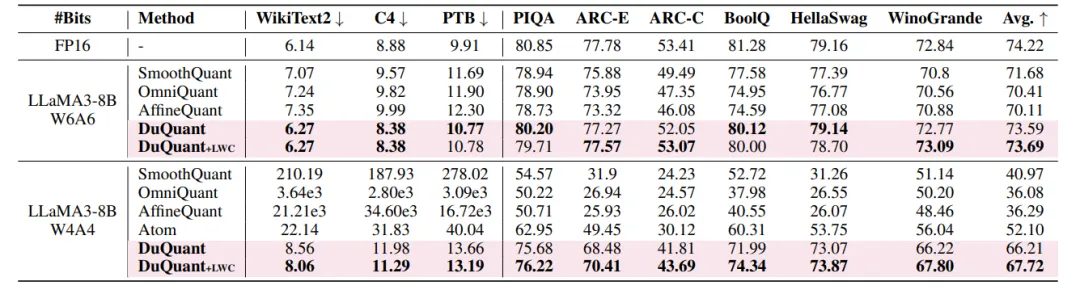△DuQuant在LLaMA3-8B的低比特量化中显著超过了基线方法
上面是DuQuant在LLaMA3模型的量化效果，更多的模型和task上的表现可以参见论文。
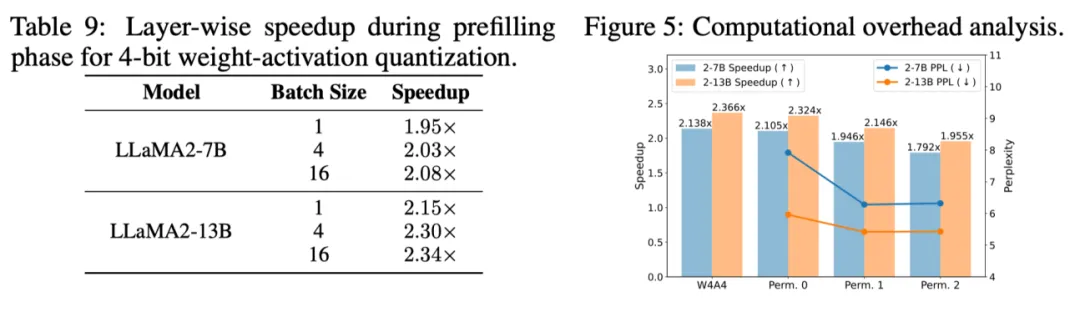
硬件测速也证明了DuQuant在pre-filing阶段可以达到2.08倍的加速比，在decoding阶段有效降低了3.50倍内存开销。
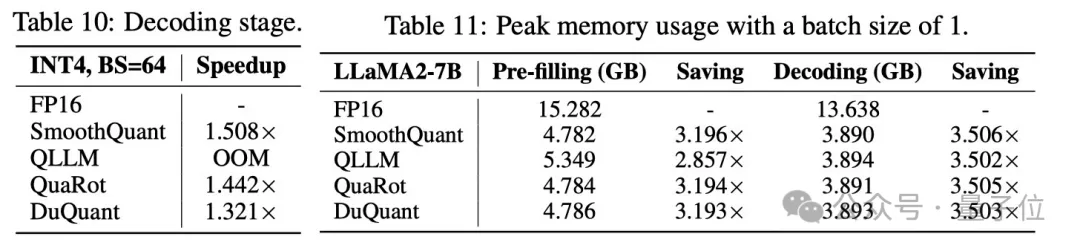
同时如右图所示，DuQuant相比INT4推理带来额外的10%左右速度开销，微高于QuaRot，但带来更多性能提升。
此外，DuQuant与使用Hadamard旋转矩阵的QuaRot主要有以下两点不同：
1、DuQuant构造的旋转矩阵利用了先验知识（具体的outlier channel索引），因此它可以比QuaRot更好地平滑激活空间，如下图展示了DuQuant单次旋转和Hadamard旋转对LLaMA2-7B Attention Key_proj输入的变换效果。
2、QuaRot依赖于耗时的GPTQ算法来提升性能，而作者引入的通道置换矩阵可以帮助DuQuant在极短时间内进一步平衡outliers的分布，两种正交变换可以同时平滑权重矩阵的空间，降低权重矩阵的量化难度，从而取得更好效果。
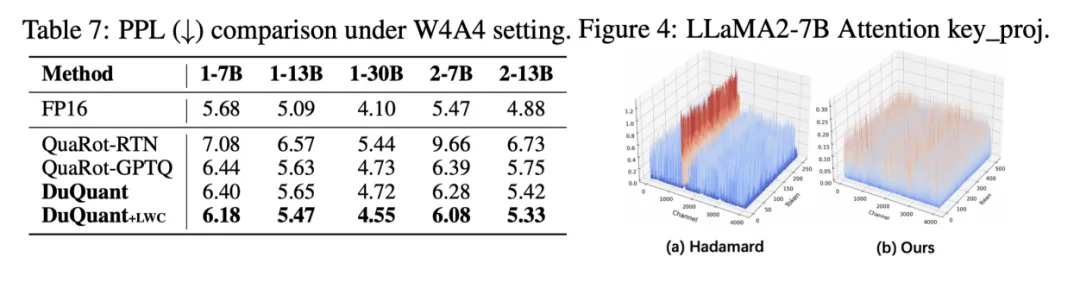
小结一下，DuQuant通过两种正交变换，利用activation激活值的先验知识达到了比QuaRot中Hadamard旋转更好的量化效果。
该工作获得了审稿人一致的高度评价，并最终被选为Oral Presentation，录取率0.4%。
更多细节欢迎查阅原论文。
项目主页：https://duquant.github.io/
论文：https://arxiv.org/abs/2406.01721
代码：https://github.com/Hsu1023/DuQuant
