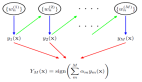
自从 ResNet 提出后，残差连接已成为深度学习模型的基础组成部分。其主要作用是 —— 缓解梯度消失问题，使得网络的训练更加稳定。
但是，现有残差连接变体在梯度消失和表示崩溃之间存在一种 “跷跷板式” 的权衡，无法同时解决。
为此，字节豆包大模型 Foundation 团队于近日提出超连接（Hyper-Connections），针对上述 “跷跷板式” 困境，实现了显著提升。
该方法适用于大规模语言模型（LLMs）的预训练，在面向 Dense 模型和 MoE 模型的实验中，展示了显著性能提升效果，使预训练收敛速度最高可加速 80%。
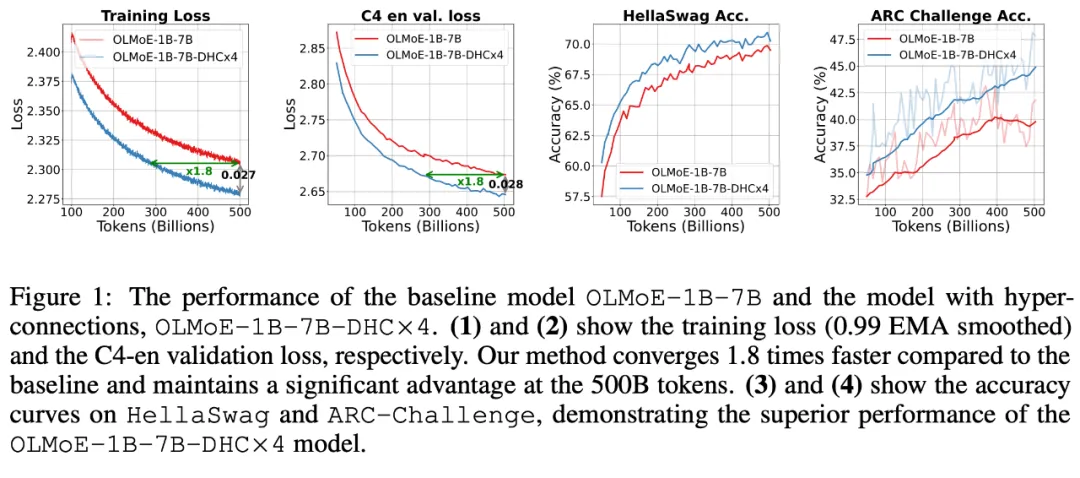
研究团队还发现，超连接在两个小型的视觉任务中表现同样优异，这表明，该方法在多个领域有广泛的应用前景。
- 论文标题：Hyper-Connections
- 论文链接：https://arxiv.org/pdf/2409.19606
1. 超连接的核心思想
前文提及，残差连接的两种主要变体 Pre-Norm 和 Post-Norm 各自都有其局限性，具体体现如下：
- Pre-Norm：在每个残差块之前进行归一化操作，可有效减少梯度消失问题。然而，Pre-Norm 在较深网络中容易导致表示崩溃，即深层隐藏表示过于相似，从而削弱了模型学习能力。
- Post-Norm：在残差块之后进行归一化操作，有助于减少表示崩溃问题，但也重新引入梯度消失问题。在 LLM 中，通常不会采用此方法。
超连接的核心思路在于 —— 引入可学习的深度连接（Depth-connections）和宽度连接（Width-connections）。
从理论上，这使得模型不仅能够动态调整不同层之间的连接强度，甚至能重新排列网络层次结构，弥补了残差连接在梯度消失和表示崩溃（Representation Collapse）之间的权衡困境。
深度连接与宽度连接
起初，该方法会将网络输入扩展为 n 个隐向量（n 称作 Expansion rate）。之后每一层的输入都会是 n 个隐向量，超连接会对这些隐向量建立以下两类连接：
- 深度连接（Depth-Connections）：这些连接类似于残差连接，只为输入与输出之间的连接分配权重，允许网络学习不同层之间的连接强度。
- 宽度连接（Width-Connections）：这些连接使得每一层多个隐藏向量之间可进行信息交换，从而提高模型表示能力。
静态与动态超连接
超连接可以是静态的，也可以是动态的。
其中，静态超连接（Static Hyper-Connections, SHC）意味着连接权重在训练结束后固定不变。而动态超连接（Dynamic Hyper-Connections, DHC）则对应连接权重可根据输入动态调整。实验表明，动态超连接效果更好。
2. 技术细节
超连接（Hyper-connections）
首先，考虑第 k 层的输入隐藏向量
，网络的初始输入为
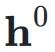，并将其复制 n 次，形成初始的超隐藏矩阵（Hyper Hidden Matrix）：
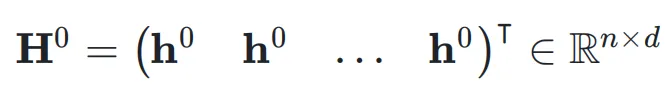
这里，n 称为扩展率（Expansion Rate）。在第 k 层，输入是上一层的超隐藏矩阵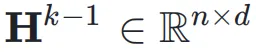
，即：
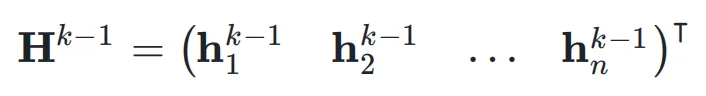
对最后一层的超隐藏矩阵逐行求和，得到所需的隐藏向量，并通过一个投影层输出网络最终的结果（在 Transformer 中即为归一化层和解嵌入层）。
为了简化后续分析的符号表示，作者省略层索引，直接将超隐藏矩阵表示为：
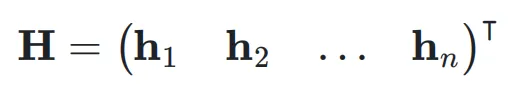
超连接可以用一个矩阵来表示，对于扩展率为 n 的情况，超连接矩阵 HC 如下：
考虑一层网络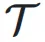
，它可能是 Transformer 中的 attention 层或者是 FFN 层。超连接的输出 
可以简单地表示为：
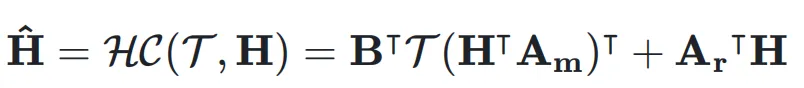
也就是说，用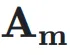 
作为权重对输入 
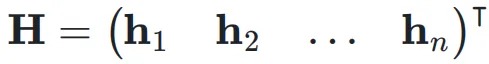进行加权求和，得到当前层的输入
：
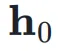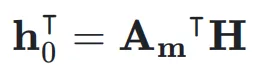
同时，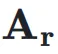
用于将 
映射到残差超隐藏矩阵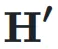
，表示如下：
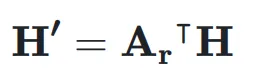
最终的输出表达式为：
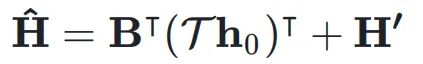
伪代码如下:
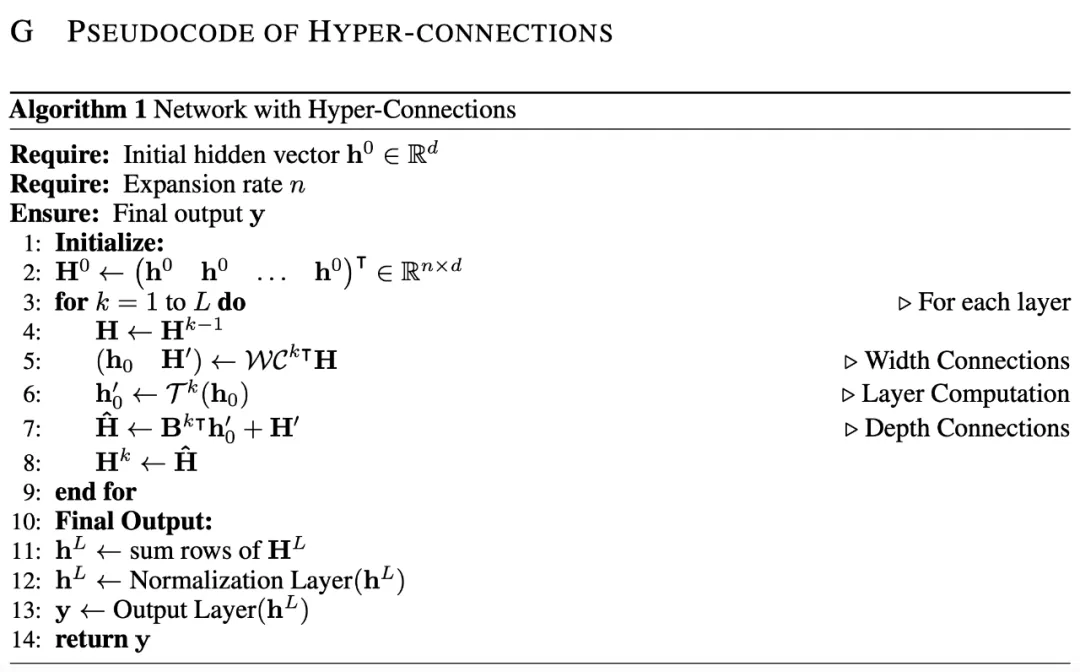
动态超连接的实现
超连接矩阵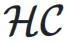 
的元素可以动态依赖于输入 
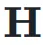，动态超连接的矩阵表示为：
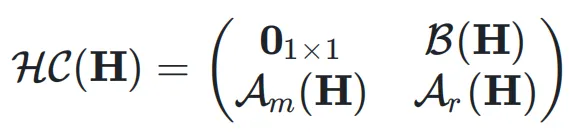
同样，给定层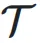 
和输入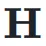
，可以得到动态超连接的输出：
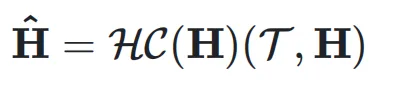
在实际操作中，团队结合了静态和动态矩阵来实现动态超连接，动态参数通过线性变换获得。
为了稳定训练过程，团队在线性变换前引入归一化，并在其后应用 tanh 激活函数，通过一个可学习的小因子进行缩放。动态参数的计算公式如下：
实验表明，动态超连接在语言建模任务中优于静态超连接。
3. 为什么使用超连接（Hyper-Connections）
研究团队认为，残差连接的两种变体，即前归一化（Pre-Norm）和后归一化（Post-Norm），可以被视为不可训练的超连接。
随后，团队引入了顺序 - 并行二象性概念，展示了超连接如何动态优化层的排列以提升网络性能。
残差连接是不可训练的超连接
前归一化和后归一化的残差连接可以表示为以下扩展率为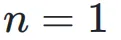 
的超连接矩阵：
其中，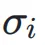
和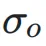 
分别表示神经网络层输入和输出的标准差，
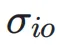表示它们之间的协方差。
对于 Pre-Norm，其超连接矩阵是一个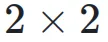 
的矩阵，右下三角部分填充为 1，其余部分为占位符 0。对于 Post-Norm，权重依赖于输入和输出的方差及协方差，形成一个 
的矩阵。因此，它们的超连接矩阵是不可训练的。
而本工作提出的方法的超连接矩阵是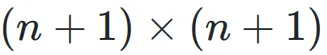 
矩阵，且权重是可训练的，甚至可以基于输入进行动态预测。
顺序 - 并行二象性
给定一系列神经网络模块，我们可以将它们顺序排列或并行排列。作者认为，超连接可以学习如何将这些层重新排列，形成顺序和并行配置的混合。
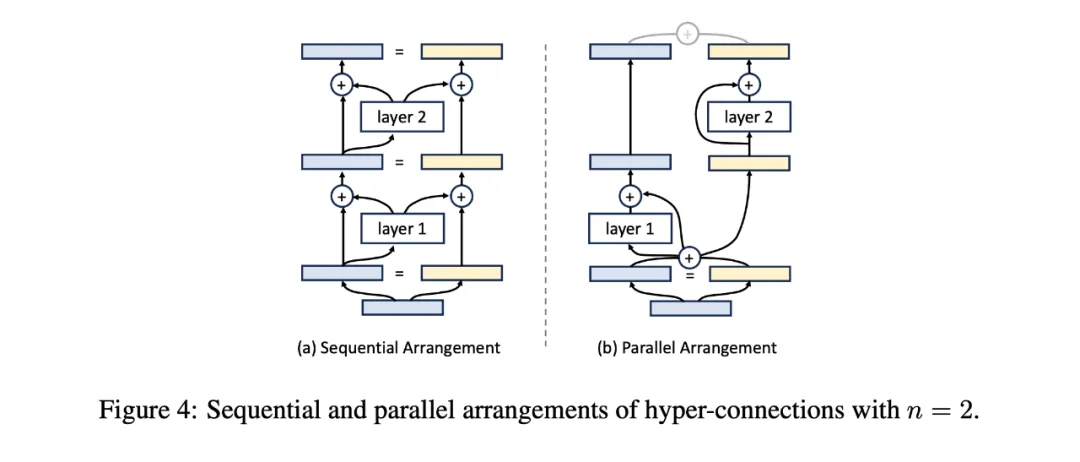
在不失一般性的情况下，可以将扩展率设置为 n=2。如果超连接以如下矩阵形式学习，神经网络将被顺序排列：
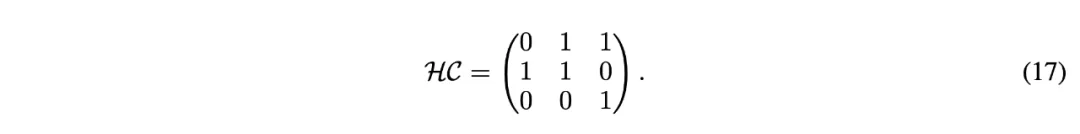
在这种情况下，深度连接退化为残差连接，如图 (a) 所示。
当奇数层和偶数层的超连接矩阵分别定义为以下形式时，神经网络每两层将被并行排列，类似于 Transformer 中的 parallel transformer block 的排列方式，如图 (b) 所示。
因此，通过学习不同形式的超连接矩阵，网络层的排列可以超越传统的顺序和并行配置，形成软混合甚至动态排列。对于静态超连接，网络中的层排列在训练后保持固定；而对于动态超连接，排列可以根据每个输入动态调整。
4. 实验结果
实验主要集中在大规模语言模型的预训练上，涵盖了 Dense 模型和 MoE 模型。
实验结果表明，使用超连接的模型显著优于使用残差连接的模型。
1B Dense 模型实验
只要扩展率 > 1，效果就十分显著，且训练更稳定，消掉了训练 loss 的 spikes。
7B Dense 模型实验
团队甚至 Scale 到了 7B 模型，效果也十分亮眼，同时可以看到有超连接的网络训练更稳定。
7B 候选激活 1.3B 的 MoE 模型实验
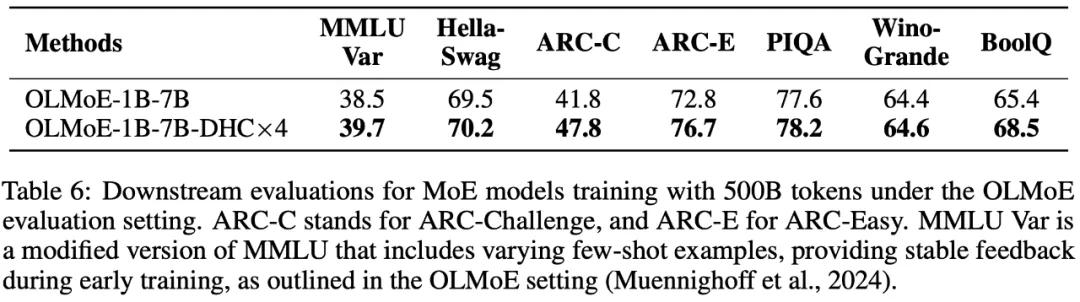
可以看到，下游指标全涨，在 ARC-Challenge 上甚至涨了 6 个百分点。
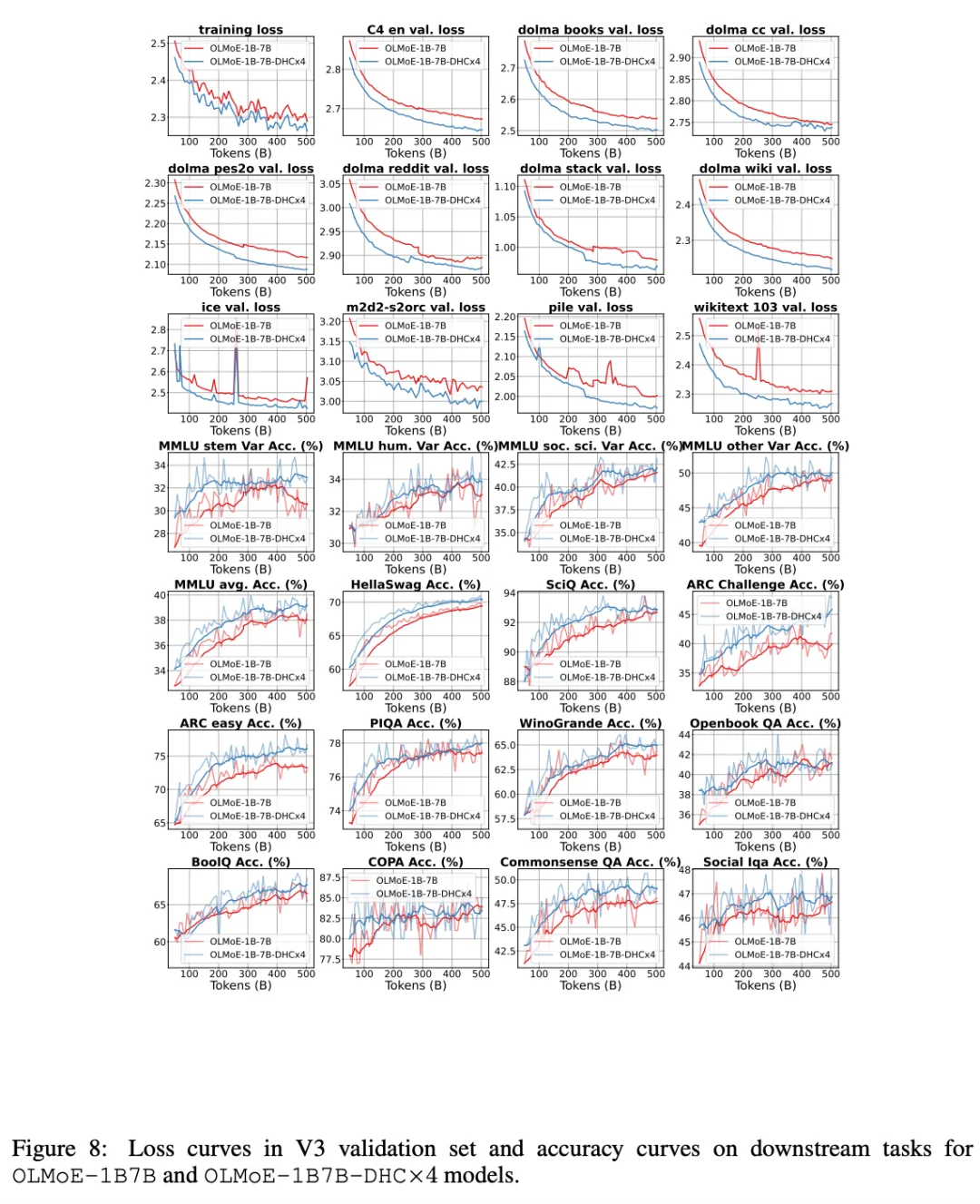
综上，研究团队介绍了超连接（Hyper-Connections），它解决了残差连接在梯度消失和表示崩溃之间的权衡问题。实验结果表明，超连接在大规模语言模型的预训练以及视觉任务中都表现出显著的性能提升。
值得注意的是，超连接的引入几乎不增加额外的计算开销或参数量，团队认为，该成果具有广泛的应用潜力，可以推广到文音视图模态的不同任务上，包括多模态理解、生成基座模型等。
5. 写在最后
团队关注底层问题，尤其在 LLMs 和多模态方面，期望实现更多突破。
更多团队技术研究进展，可以进入「豆包大模型团队」技术解读栏目了解。
