 1. Mean Squared Error (MSE)
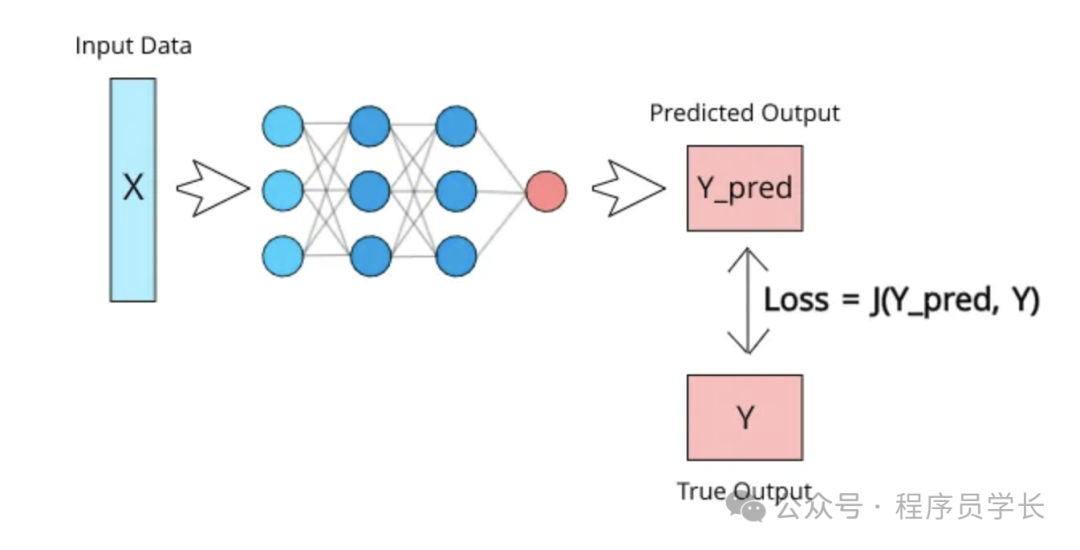
1. Mean Squared Error (MSE)
MSE 是回归任务中最常用的损失函数之一。
它衡量模型预测值与实际值之间的平均平方误差。
公式:
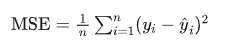
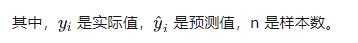
特点:
- 对于大的误差,MSE 会给出更大的惩罚,因为误差被平方。
- 对于异常值较为敏感。
import tensorflow as tf
import matplotlib.pyplot as plt
class MeanSquaredError_Loss:
"""
This class provides two methods to calculate Mean Squared Error Loss.
"""
def __init__(self):
pass
@staticmethod
def mean_squared_error_manual(y_true, y_pred):
squared_difference = tf.square(y_true - y_pred)
loss = tf.reduce_mean(squared_difference)
return loss
@staticmethod
def mean_squared_error_tf(y_true, y_pred):
mse = tf.keras.losses.MeanSquaredError()
loss = mse(y_true, y_pred)
return loss
if __name__ == "__main__":
def mean_squared_error_test(N=10, C=10):
# Generate random data
y_true = tf.random.uniform(shape=(N, ), minval=-C, maxval=C, dtype=tf.float32)
y_pred = tf.random.uniform(shape=(N, ), minval=-C, maxval=C, dtype=tf.float32)
# Test the MeanSquaredError_Loss class
mse_manual = MeanSquaredError_Loss.mean_squared_error_manual(y_true, y_pred)
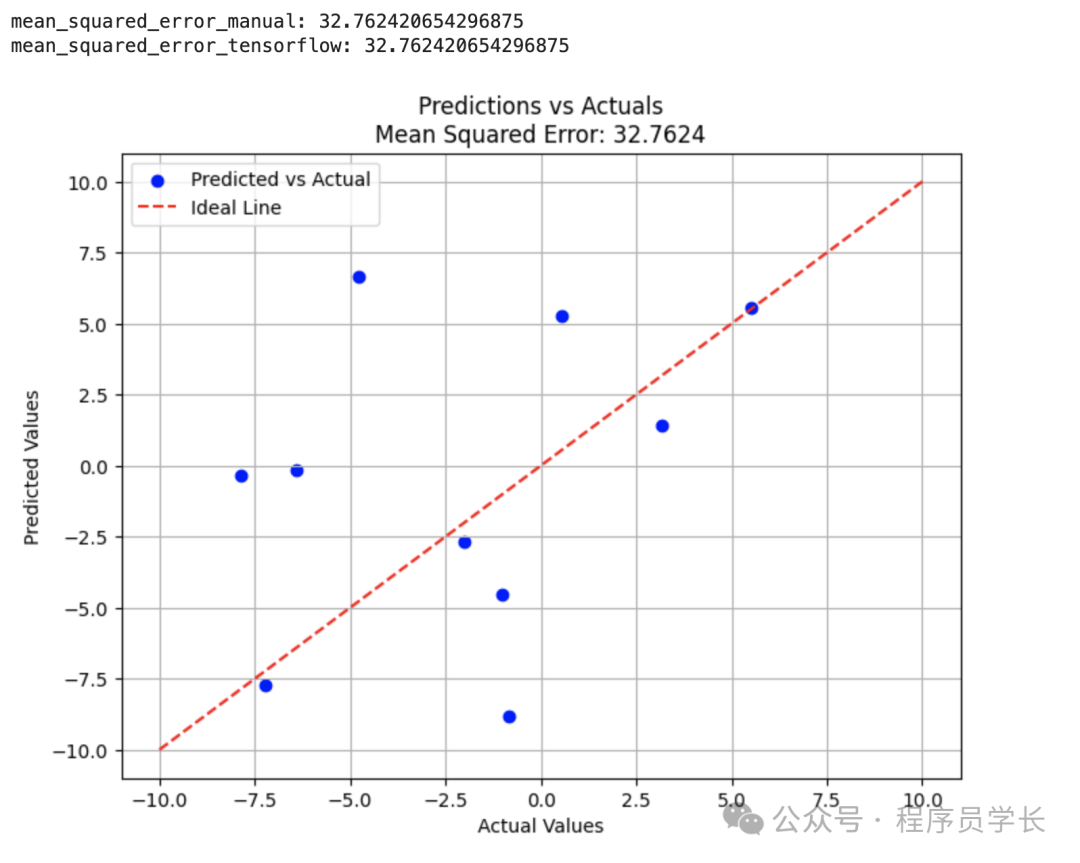
print(f"mean_squared_error_manual: {mse_manual}")
mse_tf = MeanSquaredError_Loss.mean_squared_error_tf(y_true, y_pred)
print(f"mean_squared_error_tensorflow: {mse_tf}")
print()
# Plot the points on a graph
plt.figure(figsize=(8, 6))
plt.scatter(y_true.numpy(), y_pred.numpy(), color='blue', label='Predicted vs Actual')
plt.plot([-C, C], [-C, C], 'r--', label='Ideal Line') # Diagonal line representing ideal predictions
plt.title(f"Predictions vs Actuals\nMean Squared Error: {mse_manual.numpy():.4f}")
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.grid(True)
plt.show()
mean_squared_error_test()- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
 图片
图片
2. Mean Absolute Error (MAE)
MAE 也是用于回归任务的损失函数,它计算的是预测值与实际值之间误差的绝对值的平均值。
公式:
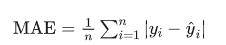
特点:
- MAE 不像 MSE 那样对异常值敏感,因为它没有平方误差。
- 更加直观,直接反映了误差的平均大小。
import tensorflow as tf
import matplotlib.pyplot as plt
class MeanAbsoluteError_Loss:
"""
This class provides two methods to calculate Mean Absolute Error Loss.
"""
def __init__(self):
pass
@staticmethod
def mean_absolute_error_manual(y_true, y_pred):
absolute_difference = tf.math.abs(y_true - y_pred)
loss = tf.reduce_mean(absolute_difference)
return loss
@staticmethod
def mean_absolute_error_tf(y_true, y_pred):
mae = tf.keras.losses.MeanAbsoluteError()
loss = mae(y_true, y_pred)
return loss
if __name__ == "__main__":
def mean_absolute_error_test(N=10, C=10):
# Generate random data
y_true = tf.random.uniform(shape=(N, ), minval=-C, maxval=C, dtype=tf.float32)
y_pred = tf.random.uniform(shape=(N, ), minval=-C, maxval=C, dtype=tf.float32)
# Test the MeanabsoluteError_Loss class
mae_manual = MeanAbsoluteError_Loss.mean_absolute_error_manual(y_true, y_pred)
print(f"mean_absolute_error_manual: {mae_manual}")
mae_tf = MeanAbsoluteError_Loss.mean_absolute_error_tf(y_true, y_pred)
print(f"mean_absolute_error_tensorflow: {mae_tf}")
print()
# Plot the points on a graph
plt.figure(figsize=(8, 6))
plt.scatter(y_true.numpy(), y_pred.numpy(), color='blue', label='Predicted vs Actual')
plt.plot([-C, C], [-C, C], 'r--', label='Ideal Line') # Diagonal line representing ideal predictions
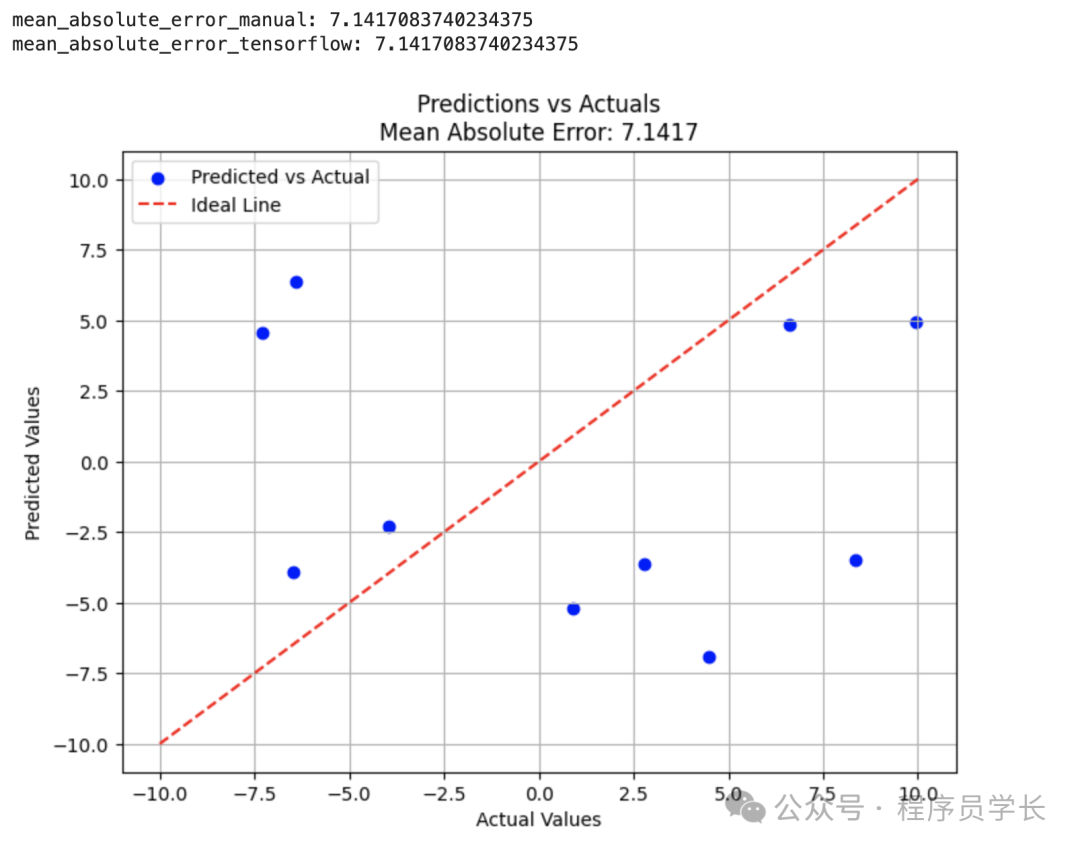
plt.title(f"Predictions vs Actuals\nMean Absolute Error: {mae_manual.numpy():.4f}")
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.grid(True)
plt.show()
mean_absolute_error_test()- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
 图片
图片
3. Huber Loss
Huber Loss 是介于 MSE 和 MAE 之间的一种损失函数,当误差较小时,它像 MSE 一样处理,而当误差较大时,它像 MAE 一样处理。
这样可以在处理异常值时更稳定。
公式:
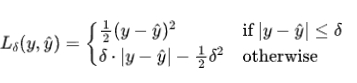

特点:
- 对异常值更具有鲁棒性,同时保留了误差较小时的敏感性。
import tensorflow as tf
import matplotlib.pyplot as plt
class Huber_Loss:
"""
This class provides two methods to calculate Huber Loss.
"""
def __init__(self, delta = 1.0):
self.delta = delta
def huber_loss_manual(self, y_true, y_pred):
error = tf.math.abs(y_true - y_pred)
is_small_error = tf.math.less_equal(error, self.delta)
small_error_loss = tf.math.square(error) / 2
large_error_loss = self.delta * (error - (0.5 * self.delta))
loss = tf.where(is_small_error, small_error_loss, large_error_loss)
loss = tf.reduce_mean(loss)
return loss
def huber_loss_tf(self, y_true, y_pred):
huber_loss = tf.keras.losses.Huber(delta = self.delta)(y_true, y_pred)
return huber_loss
if __name__ == "__main__":
def huber_loss_test(N=10, C=10):
# Generate random data
y_true = tf.random.uniform(shape=(N, ), minval=-C, maxval=C, dtype=tf.float32)
y_pred = tf.random.uniform(shape=(N, ), minval=-C, maxval=C, dtype=tf.float32)
# Test the Huber_Loss class
huber = Huber_Loss()
hl_manual = huber.huber_loss_manual(y_true, y_pred)
print(f"huber_loss_manual: {hl_manual}")
hl_tf = huber.huber_loss_tf(y_true, y_pred)
print(f"huber_loss_tensorflow: {hl_tf}")
print()
# Plot the points on a graph
plt.figure(figsize=(8, 6))
plt.scatter(y_true.numpy(), y_pred.numpy(), color='blue', label='Predicted vs Actual')
plt.plot([-C, C], [-C, C], 'r--', label='Ideal Line') # Diagonal line representing ideal predictions
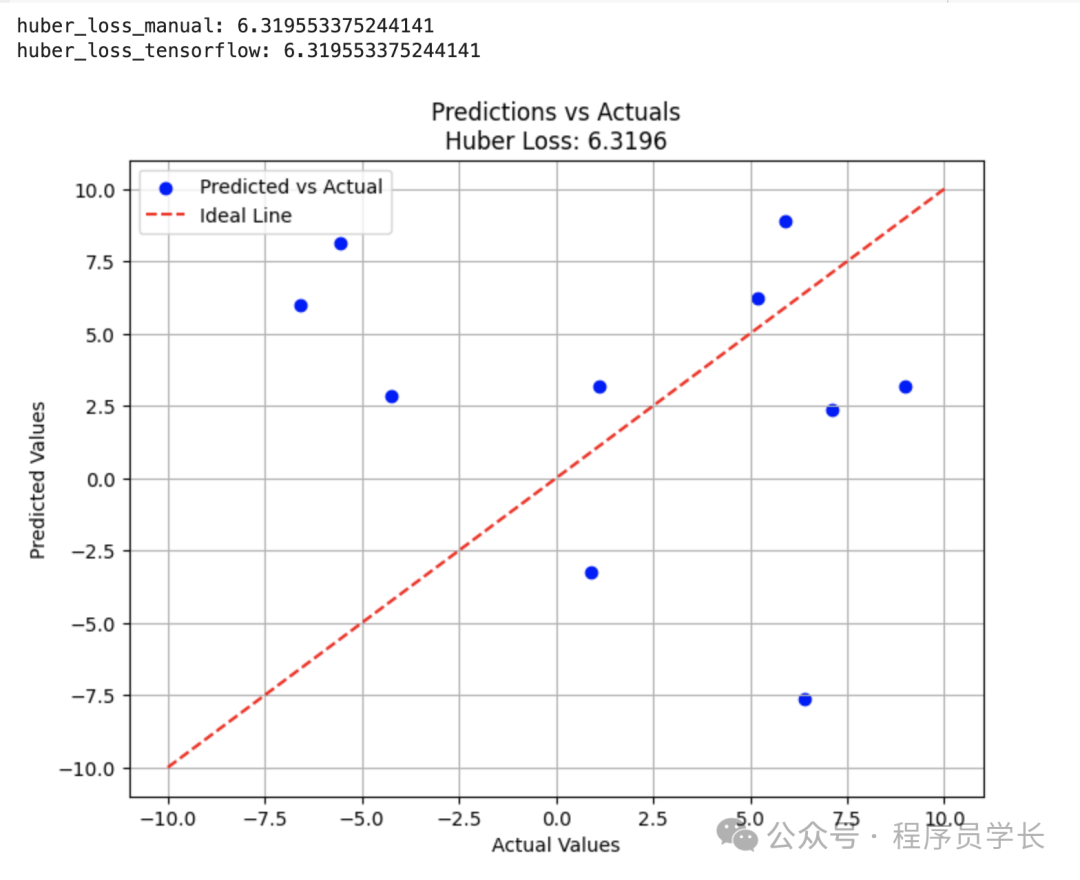
plt.title(f"Predictions vs Actuals\nHuber Loss: {hl_manual.numpy():.4f}")
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.grid(True)
plt.show()
huber_loss_test()- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
 图片
图片
4. Cross-Entropy Loss
Cross-Entropy Loss 是分类任务中广泛使用的损失函数,尤其是在二分类和多分类问题中。
它衡量的是模型输出的概率分布与实际类别的分布之间的差异。
公式:
对于二分类问题:
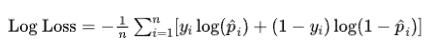

特点:
- 当预测概率与实际标签匹配时,损失较低;否则损失较高。
- 对于分类问题的优化尤为有效。
import tensorflow as tf
import matplotlib.pyplot as plt
class Cross_Entropy_Loss:
"""
This class provides two methods to calculate Cross-Entropy Loss.
"""
def __init__(self):
pass
def cross_entropy_loss_manual(self, y_true, y_pred):
y_pred /= tf.reduce_sum(y_pred)
epsilon = tf.keras.backend.epsilon()
y_pred_new = tf.clip_by_value(y_pred, epsilon, 1.)
loss = - tf.reduce_sum(y_true * tf.math.log(y_pred_new))
return loss
def cross_entropy_loss_tf(self, y_true, y_pred):
loss = tf.keras.losses.categorical_crossentropy(y_true, y_pred)
return loss
if __name__ == "__main__":
def cross_entropy_loss_test(N=10, C=1):
# Generate random data
y_true = tf.random.uniform(shape=(N, ), minval=-C, maxval=C, dtype=tf.float32)
y_pred = tf.random.uniform(shape=(N, ), minval=-C, maxval=C, dtype=tf.float32)
# Test the Cross-Entropy_Loss class
cross_entropy = Cross_Entropy_Loss()
ce_manual = cross_entropy.cross_entropy_loss_manual(y_true, y_pred)
print(f"cross_entropy_loss_manual: {ce_manual}")
ce_tf = cross_entropy.cross_entropy_loss_tf(y_true, y_pred)
print(f"cross_entropy_loss_tensorflow: {ce_tf}")
print()
# Plot the points on a graph
plt.figure(figsize=(8, 6))
plt.scatter(y_true.numpy(), y_pred.numpy(), color='blue', label='Predicted vs Actual')
plt.plot([-C, C], [-C, C], 'r--', label='Ideal Line') # Diagonal line representing ideal predictions
plt.title(f"Predictions vs Actuals\nCross-Entropy Loss: {ce_manual.numpy():.4f}")
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.grid(True)
plt.show()
cross_entropy_loss_test()- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
5. Hinge Loss
Hinge Loss 通常用于支持向量机(SVM)中。
它鼓励模型使得正确类别的得分高于错误类别至少一个边距(通常是1)。
公式:
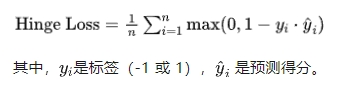
特点:
- 强制模型为正确类别创造一个“边距”,使得分类更加鲁棒。
- 适用于线性分类器的优化。
import tensorflow as tf
import matplotlib.pyplot as plt
class Hinge_Loss:
"""
This class provides two methods to calculate Hinge Loss.
"""
def __init__(self):
pass
def hinge_loss_manual(self, y_true, y_pred):
pos = tf.reduce_sum(y_true * y_pred, axis=-1)
neg = tf.reduce_max((1 - y_true) * y_pred, axis=-1)
loss = tf.maximum(0, neg - pos + 1)
return loss
def hinge_loss_tf(self, y_true, y_pred):
loss = tf.keras.losses.CategoricalHinge()(y_true, y_pred)
return loss
if __name__ == "__main__":
def hinge_loss_test(N=10, C=10):
# Generate random data
y_true = tf.random.uniform(shape=(N, ), minval=-C, maxval=C, dtype=tf.int32)
y_pred = tf.random.uniform(shape=(N, ), minval=-C, maxval=C, dtype=tf.int32)
# Test the Hinge_Loss class
cross_entropy = Hinge_Loss()
hl_manual = cross_entropy.hinge_loss_manual(y_true, y_pred)
print(f"hinge_loss_manual: {hl_manual}")
hl_tf = cross_entropy.hinge_loss_tf(y_true, y_pred)
print(f"hinge_loss_tensorflow: {hl_tf}")
print()
# Plot the points on a graph
plt.figure(figsize=(8, 6))
plt.scatter(y_true.numpy(), y_pred.numpy(), color='blue', label='Predicted vs Actual')
plt.plot([-C, C], [-C, C], 'r--', label='Ideal Line') # Diagonal line representing ideal predictions
plt.title(f"Predictions vs Actuals\nHinge Loss: {hl_manual.numpy()}")
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.grid(True)
plt.show()
hinge_loss_test()- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
6. Intersection Over Union (IoU)
IoU 通常用于目标检测任务中,衡量预测的边界框与实际边界框之间的重叠程度。
公式:

特点:
- 值域在0到1之间,1表示完美重叠,0表示没有重叠。
- 用于评估边界框预测的准确性。
import tensorflow as tf
import matplotlib.pyplot as plt
class IOU:
def __init__(self):
pass
def IOU_manual(self, y_true, y_pred):
intersection = tf.reduce_sum(tf.cast(tf.logical_and(tf.equal(y_true, 1), tf.equal(y_pred, 1)), dtype=tf.float32))
union = tf.reduce_sum(tf.cast(tf.logical_or(tf.equal(y_true, 1), tf.equal(y_pred, 1)), dtype=tf.float32))
iou = intersection / union
return iou
def IOU_tf(self, y_true, y_pred):
iou_metric = tf.keras.metrics.IoU(num_classes=2, target_class_ids=[1])
iou_metric.update_state(y_true, y_pred)
iou = iou_metric.result()
return iou
if __name__ == "__main__":
def IOU_test(N=10, C=10):
# Generate random data
y_true = tf.random.uniform(shape=(N, ), minval=-C, maxval=C, dtype=tf.int32)
y_pred = tf.random.uniform(shape=(N, ), minval=-C, maxval=C, dtype=tf.int32)
y_true = tf.constant([[0, 1, 1, 0],
[0, 1, 1, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=tf.float32) # Example binary mask (ground truth)
y_pred = tf.constant([[0, 1, 1, 0],
[1, 1, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=tf.float32) # Example binary mask (prediction)
iou = IOU()
iou_manual = iou.IOU_manual(y_true, y_pred)
print(f"IOU_manual: {iou_manual}")
iou_tf = iou.IOU_tf(y_true, y_pred)
print(f"IOU_tensorflow: {iou_tf}")
IOU_test()- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
7. Kullback-Leibler (KL) Divergence
KL 散度是一种衡量两个概率分布之间差异的非对称性度量,通常用于生成模型和变分自编码器中。
公式:

特点:
- 当 P 和 Q 完全相同时,KL 散度为0。
- 适用于评估模型预测的概率分布与目标概率分布之间的差异。
import tensorflow as tf
import matplotlib.pyplot as plt
class Kullback_Leibler:
"""
This class provides two methods to calculate Kullback-Leibler Loss.
"""
def __init__(self):
pass
def kullback_leibler_manual(self, y_true, y_pred):
epsilon = tf.keras.backend.epsilon()
y_true = tf.clip_by_value(y_true, epsilon, 1)
y_pred = tf.clip_by_value(y_pred, epsilon, 1)
loss = tf.reduce_sum(y_true * tf.math.log(y_true / y_pred), axis=-1)
return loss
def kullback_leibler_tf(self, y_true, y_pred):
loss = tf.reduce_sum(tf.keras.losses.KLDivergence()(y_true, y_pred))
return loss
if __name__ == "__main__":
def kullback_leibler_test(N=5, C=1):
# Generate random data
y_true = tf.random.uniform(shape=(N, ), minval=0, maxval=C, dtype=tf.float32)
y_pred = tf.random.uniform(shape=(N, ), minval=0, maxval=C, dtype=tf.float32)
#converting them to probabilities
y_true /= tf.reduce_sum(y_true)
y_pred /= tf.reduce_sum(y_pred)
# Test the kullback_leibler class
kl = Kullback_Leibler()
kl_manual = kl.kullback_leibler_manual(y_true, y_pred)
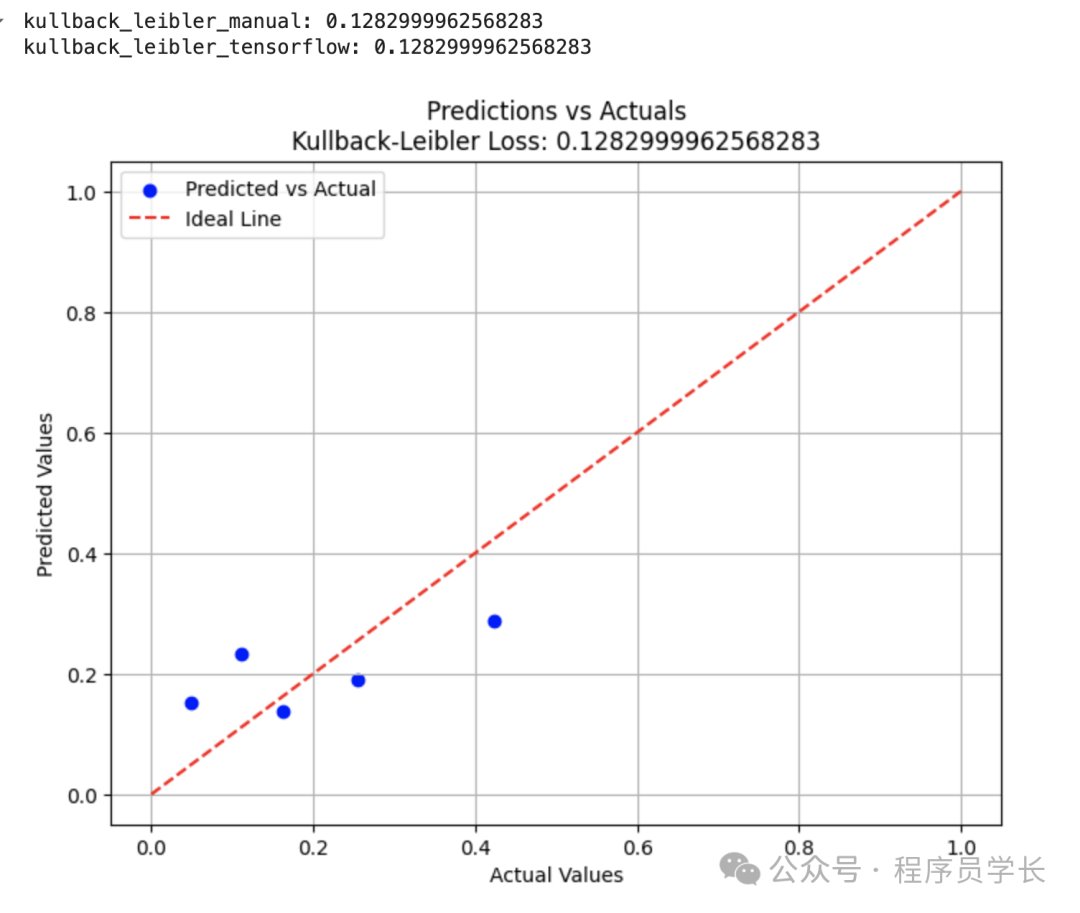
print(f"kullback_leibler_manual: {kl_manual}")
kl_tf = kl.kullback_leibler_tf(y_true, y_pred)
print(f"kullback_leibler_tensorflow: {kl_tf}")
print()
# Plot the points on a graph
plt.figure(figsize=(8, 6))
plt.scatter(y_true.numpy(), y_pred.numpy(), color='blue', label='Predicted vs Actual')
plt.plot([0, C], [0, C], 'r--', label='Ideal Line') # Diagonal line representing ideal predictions
plt.title(f"Predictions vs Actuals\nKullback-Leibler Loss: {kl_manual.numpy()}")
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.grid(True)
plt.show()
kullback_leibler_test()- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
 图片
图片












































