一种高效的顺序划分算法——循环划分算法

译者 | 朱先忠

审校 | 重楼

摘要：本文将详细介绍一种新颖高效的顺序划分算法——循环划分算法，它能够对普通类型值数据进行最小次数的重新排列。

1.导言

顺序划分是计算机编程中一种基本且常用的算法。给定一个数字序列“A”和一个称为基准值的值“p”，划分算法的目的是以这种方式重新排列“A”中的数字，使所有小于“p”的数字排在第一位，然后是其余的数字。

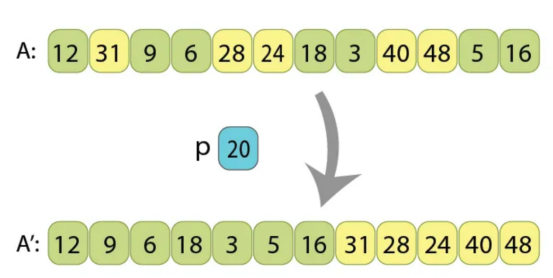
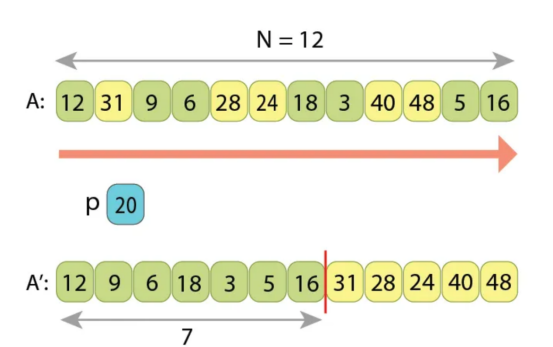
按基准值“p=20”划分前后的序列示例。应用算法后，所有小于20的值（浅绿色）显示在其他值之前（黄色）。

划分算法有不同的应用，但最受欢迎的应用包括：

• 快速排序（QuickSort）——一种划分算法，在给定数组的不同子数组上通过递归多次调用，直到最终完成排序。
• 找到给定序列的中值——利用划分来有效地缩小搜索范围，并最终在预期的线性时间内找到中值。

对序列进行排序是在大量数据上实现更快导航的重要步骤。在两种常见的搜索算法中——线性搜索和二分查找——后者只有在数组中的数据被排序时才能使用。找到中位数或k阶统计量对于理解给定未排序数据中的值分布至关重要。

目前已经存在不同的划分算法（也称为划分方案），但最著名的要算是“Lomuto方案”和“Hoare方案”。Lomuto方案通常直观上更容易理解，而Hoare方案在给定数组内的重排次数较少，这就是它在实践中通常更受欢迎的原因。

在本文中，我要推荐的是一种新的划分方案，称为“循环划分”，它类似于Hoare方案，但数组内的重新排列（值赋值）要少1.5倍。因此，正如稍后将显示的那样，值赋值的数量几乎等于最初“不在原位”的值的数量，并且应该以某种方式移动。这一事实让我认为这个新的划分方案几乎是最优的。

接下来的内容按以下方式组织：

• 在第2节中，我们将回顾什么是就地划分（一种属性，它使得划分操作不那么繁杂）
• 在第3节中，我们将回顾广泛使用的Hoare划分方案
• 在第4节中，我将介绍“循环赋值”，我们将了解为什么序列的某些重排可能需要比同一序列的其他重排更多的值赋值
• 第5节将利用“赋值循环”的一些性质，推导出新的“循环划分”方案，作为Hoare方案的优化变体
• 最后，第6节将对小数据类型和大数据类型的数组进行Hoare方案和循环划分的实验比较。

请注意，GitHub上已经提供了基于C++语言的循环划分的实现，以及它与当前标准Hoare方案的基准测试，详见本文末尾的引用文献。

2.原地顺序划分回顾

如果输入和输出序列位于计算机内存中的2个不同数组中，则对序列进行划分将不是一项艰巨的任务。如果情况是这样的话，那么其中一种方法可能是：

• 计算“A”中有多少值小于“p”（这将给出输出序列左半部分的最终长度）
• 从左到右扫描输入数组“A”，并将每个当前值“A[i]”附加到左侧或右侧，具体取决于它是否小于“p”。

以下是运行此类算法的几个状态：

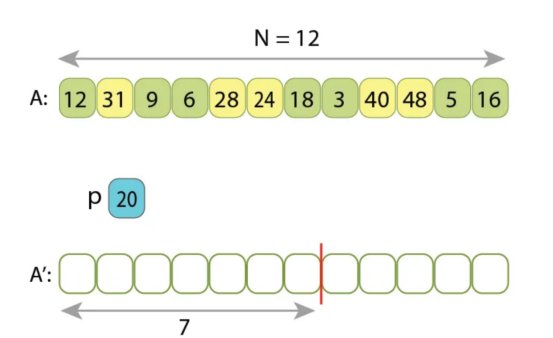
在第一阶段，我们计算出只有7个值小于“p=20”（浅绿色的值），因此我们准备从索引7开始将较大的值写入输出序列。

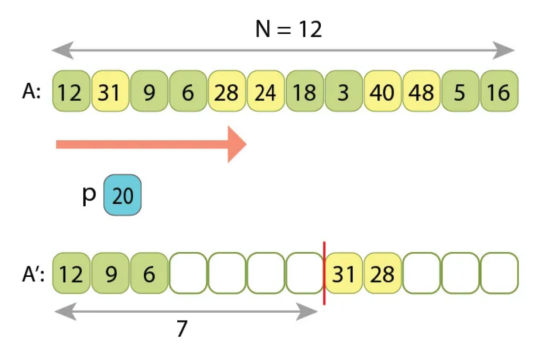
在第二阶段扫描输入序列的5个值之后，我们将其中的3个附加到输出序列的左侧部分，另两个在其右侧。

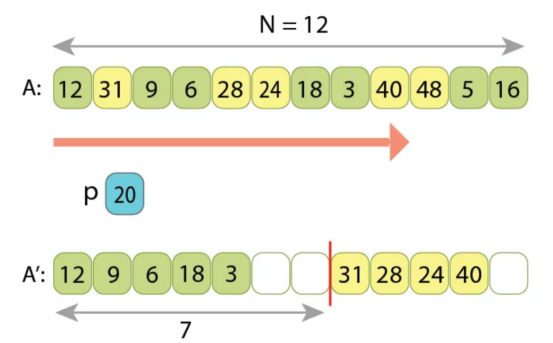
继续第二阶段，我们现在从输入序列中扫描了9个值，将其中5个放置在输出序列的左侧，将另外4个放置在其右侧。

算法完成（现在，输出序列的两个部分都已正确填充到末尾）

注意，这里保留了左边部分或右边部分中数值的相对顺序（根据它们最初在输入数组中的写入方式）。

当然，还有其他更简短的解决方案，比如代码中只有一个循环的解决方案。

现在，当我们不想使用任何额外的内存时，困难就来了。因此，只需在唯一的数组中移动值，输入序列就会被转换为划分后的输出序列。顺便说一句，这种不使用额外内存的算法称为就地算法。

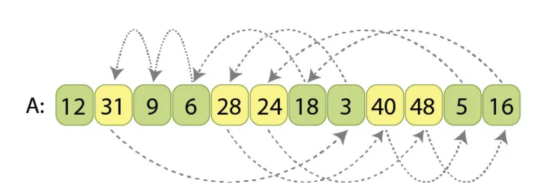
用相同的基准值“p=20”对相同的输入序列“A”进行划分

这里显示的值顺序对应于序列的输入状态，每个值都显示箭头——如果应该将该值移动到某处，以便对整个序列进行划分。

在介绍我的划分方案之前，让我们首先来回顾一下现有的和常用的就地划分解决方案。

3.目前使用的划分方案

在观察了各种编程语言的标准库中排序的一些实现后，看起来使用最广泛的划分算法是Hoare方案。我发现它被用于例如：

• C++STL中的“std::sort()”实现
• JDK for Java中用于原始数据类型的“Arrays.sort()”实现

在基于Hoare方案的划分中，我们从两端向彼此同时扫描序列，在左侧部分搜索大于或等于'p'的a[i]值，在右侧部分搜索小于'p'的a[j]值。一旦找到，我们就知道这两个值A[i]和A[j]都属于“不在它们的正确位置”（记住，划分序列应该先有小于'p'的值，然后才有大于或等于'p'所有其他值），所以我们只需要交换A[i]与A[j]。交换后，我们继续以同样的方式，同时扫描索引为i和j的数组“A”，直到它们相等。一旦完成，划分就完成了。

让我们在另一个例子中观察Hoare方案：

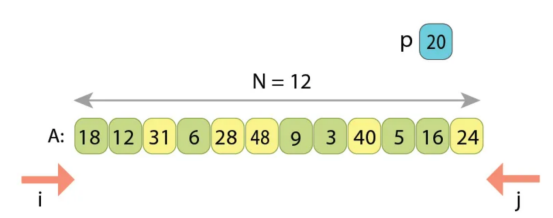
长度为'N'的输入序列“A”，应按基准值“p=20”进行划分

索引i从0开始向上扫描，索引j从“N-1”开始向下扫描。

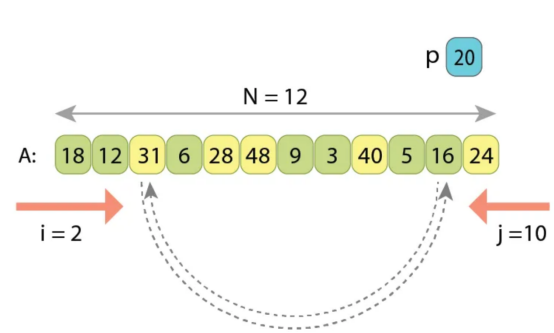
当增加索引i时，我们会遇到值“A[2]=31”，它大于“p”。然后，在减小索引j之后，我们遇到另一个值“A[10]=16”，它小于'p'。这两个将被交换。

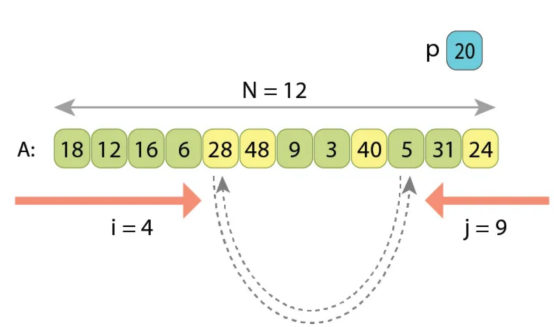
在交换“A[2]”和“A[10]”之后，我们继续从2增加i，从10减少j。索引i将在大于'p'的值“A[4]=28”时停止，索引j将在小于'p]的值“A[9]=5”时停止。这两个也将被交换。

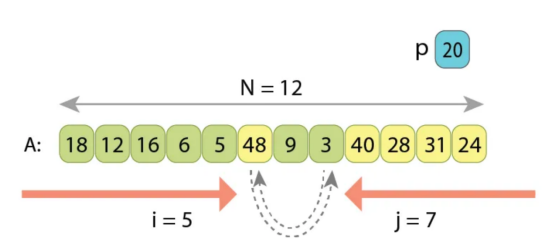
算法以同样的方式继续，数字“A[5]=48”和“A[7]=3”也将被交换。

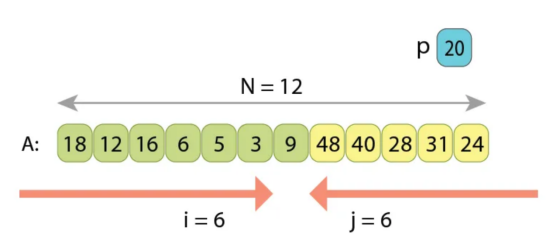
之后，索引“i”和“j”将彼此相等。至此，划分算法完成。

如果用Hoare方案编写划分的伪代码，我们将得到以下内容：

// 对序列A[0..N)进行划分，使用基准值 'p' 
// 根据Hoare方案，并返回结果右边部分第一个值的索引。
function partition_hoare( A[0..N) : Array of Integers, p: Integer ) : Integer
 i := 0
 j := N-1
 while true
 // 根据需要向左移动索引“i”
 while i < j and A[i] < p
 i := i+1
 // 根据需要向右移动索引“j”
 while i < j and A[j] >= p
 j := j-1
 // Check for completion
 if i >= j
 if i == j and A[i] < p
 return i+1 // "A[i]" 指向左边部分
 else
 return i // "A[i]"指向右边部分 
//交换"A[i]"和"A[j]"
 tmp := A[i]
 A[i] := A[j]
 A[j] := tmp
 //'i'和'j'各自加1
 i := i+1
 j := j-1

在第5行和第6行中，我们为2次扫描设置了开始索引。

第8-10行从左侧搜索这样一个值，该值在划分后应属于右侧。

同样，第11-13行从右侧搜索这样一个值，它应该属于左侧。

第15-19行检查扫描是否完成。一旦索引'i'和'j'相遇，就有两种情况：“A[i]”属于左部分或右部分。根据这一点，我们返回“i”或“i+1”，因为函数的返回值应该是右侧部分的开始索引。

接下来，如果扫描尚未完成，第20-23行会交换那些不在正确位置的2个值。

最后，第24-26行各自把这两个索引加1，以便不重新检查已经交换的值。

该算法的时间复杂度为O（N），无论两次扫描在哪里相遇，因为它们总是一起扫描N个值。

这里有一个重要的注意事项，如果数组“A”的'L'值“不在它们的位置”，并且应该被交换，那么按照Hoare方案，我们将进行“3*L/2”赋值，因为交换2个值需要3个赋值：

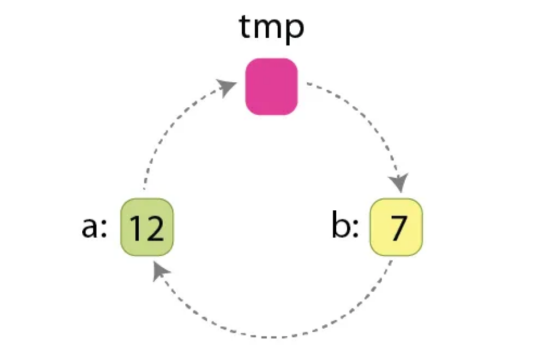
交换2个变量“a”和“b”的值，需要在“tmp”变量的帮助下进行3次赋值。

这些任务是：

tmp := a

a := b

b := tmp

需要强调一下，“L”总是偶数。这是因为对于最初位于左侧区域的每个值“A[i]>=p”，都有另一个值“A[j]<p”最初位于右侧区域，这些值正在被交换。因此，每次交换都会重新排列2个这样的值，Hoare方案中的所有重新排列都是通过交换完成的。这就是为什么“L”——要重新排列的值的总数——总是偶数。

4.循环赋值

本节内容可能看起来与本文主题有所偏离，但实际上并非如此，因为在优化Hoare划分方案时，我们需要在下一节中了解循环赋值的知识。

假设我们想以某种方式重新排列给定序列“A”中的值的顺序。这不一定是划分，而是任何形式的重新排列。让我来证明一下，一些重排列需要比其他一些排列更多的赋值操作。

情形1：序列的循环左移

如果我们想将序列“A”循环左移1个位置，应该完成多少个赋值操作？

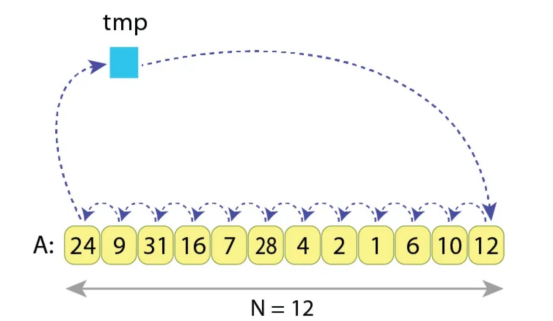
长度为N=12的序列“A”的循环左移示例

我们看到所需的赋值操作数量为N+1=13，因为我们需要：

1）将“A[0]”存储在临时变量“tmp”中，然后

2）“N-1”次将右相邻值赋值给当前值，最后

3）将“tmp”赋值给序列“A[N-1]”的最后一个值。

要做到这一点，所需的操作是：

tmp := A[0]
A[0] := A[1]
A[1] := A[2]
...
A[9] := A[10]
A[10] := A[11]
A[11] := tmp

……这导致了13次赋值操作。

情形2：循环左移3个位置

在下一个例子中，我们仍然想对同一序列进行循环左移，但现在向左移动3个位置：

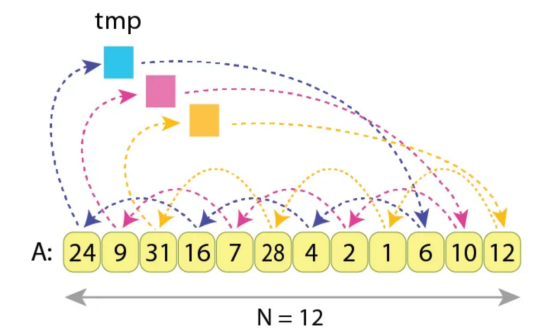序列“A”的循环左移3的示例，长度N=12

我们看到值A[0]、A[3]、A[6]和A[9]正在相互交换（蓝色箭头）

以及值A[1]、A[4]、A[7]和A[10]（粉红色箭头）

并且由于值A[2]、A[5]、A[8]和A[11]仅在彼此之间交换（黄色箭头）。

“tmp”变量被赋值和读取了3次。

这里我们有3个独立的赋值链/循环，每个长度为4。

为了在A[0]、A[3]、A[6]和A[9]之间正确交换值，需要采取以下行动：

tmp := A[0]
A[0] := A[3]
A[3] := A[6]
A[6] := A[9]
A[9] := tmp

……这里进行了5次赋值。同样，在组（A[1]，A[4]，A[7]，A[10]）和（A[2]，A[5]，A[8]，A[11]）内交换值将需要分别进行5次赋值。将所有这些加在一起，得到了将序列“A”循环左移3所需的5*3=15个赋值，其中N=12个值。

情形3：颠倒顺序

当反转长度为“N”的序列“A”时，执行的操作是：

• 将其第一个值与最后一个值交换，然后
• 将第二个值与右侧的第二个进行交换，
• 将第三个值与右侧的第三个进行交换，
• ……等等。

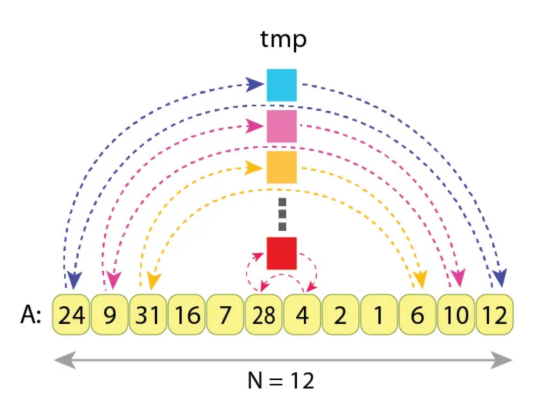反转数组“A”的示例，其中N=12个值

我们看到成对的值（A[0]，A[11]），（A[1]，A[10]），（A[2]，A[9]）等正在相互独立地交换。变量“tmp”被赋值和读取6次。

由于每个交换都需要3次赋值，而对于反转整个序列“A”，我们需要进行N/2交换，因此赋值的总数为：

3*N/2=3*12/2=3*6=18

与“A”相反的赋值的确切顺序是：

tmp := A[0] // 循环1
A[0] := A[11]
A[11] := tmp
tmp := A[1] // 循环2
A[1] := A[10]
A[10] := tmp

...

tmp := A[5] // 循环6
A[5] := A[6]
A[6] := tmp

小结

我们已经看到，重新排列相同序列“A”的值可能需要不同数量的赋值，具体取决于重新排列值的确切方式。

在所提供的3个示例中，序列的长度始终为N=12，但所需分配的数量不同：

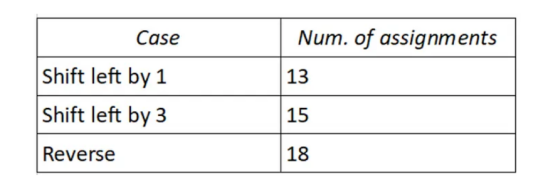
更确切地说，赋值次数等于N+C，其中“C”是重排过程中产生的循环次数。在这里，我所说的“循环”是指“a”的变量子集，其值在彼此之间旋转。

在我们的例子1（左移1）中，我们只有C=1个赋值循环，“A”的所有变量都参与了这个周期。这就是为什么赋值总数是：

N+C=12+1=13。

在情形2（左移3）中，我们有C=3个赋值循环，其中：

变量内的第一个循环（A[0]、A[3]、A[6]、A[9]）

第二个循环应用于变量（A[1]、A[4]、A[7]、A[10]）

第三个循环应用于变量（A[2]，A[5]，A[8]，A[11]）。

这就是为什么赋值总数是：

N+C=12+3=15。

在我们的情形3（反转）中，我们有⌊N/2⌋=12/2=6个周期。这些都是最短的可能循环，并应用于配对（A[0]，A[11]），（A[1]，A[10]），…等等。这就是为什么赋值的总数是：

N+C=12+6=18。

当然，在所提供的示例中，赋值数量的绝对差异非常小，在编写高性能代码时不会起任何作用。但这是因为我们考虑了一个长度为“N=12”的非常短的数组。对于较长的数组，赋值数量的差异将与N成比例增长。

在结束本节时，让我们记住，重新排列序列所需的赋值数量会随着这种重新排列所引入的循环数量而增长。如果我们想更快地重新排列，我们应该尝试通过这样一个方案来实现，该方案具有尽可能少的赋值循环。

5.优化Hoare划分方案

现在，让我们再次观察Hoare划分方案，这次要注意它引入了多少个赋值循环。

假设我们有一个长度为N的相同数组“A”，以及一个必须根据其进行划分的基准值“p”。另外，让我们假设数组中有'L'值，应该以某种方式重新排列，以便将“A”带入划分状态。事实证明，Hoare划分方案以最慢的方式重新排列这些“L”值，因为它引入了最大可能的赋值循环数，每个循环仅由2个值组成。

给定基准值“p=20”，应重新排列的“L=8”值是朝箭头方向（或离开箭头方向）。

Hoare划分方案引入了“L/2=4”个赋值循环，每个循环只作用于2个值。

在长度为2的循环中移动2个值，本质上就是交换它们，需要3次赋值。因此，Hoare划分方案的值赋值总数为“3*L/2”。

我将要描述的优化背后的想法来自这样一个事实，即在对序列进行划分后，我们通常对值“a[I]<p”的相对顺序不感兴趣，这些值应该在划分序列的左侧结束，我们也不关心值的相对顺序，这些值应在右侧结束。我们唯一感兴趣的是，所有小于“p”的值都排在其他值之前。这一事实允许我们改变Hoare方案中的赋值循环，并只产生一个赋值循环，其中包含所有的“L”值，这些值应该以某种方式重新排列。

让我先借助下图描述一下更改后的划分方案：

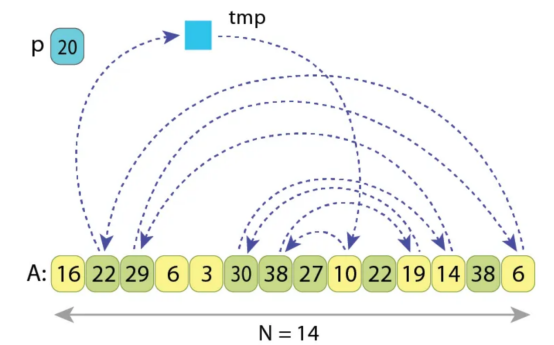更改后的划分方案，应用于相同的序列“A”

由于基准值“p=20”没有改变，因此应重新排列的“L=8”值也相同。

所有箭头代表新方案中唯一的赋值循环。

在将所有“L”值移动到它上面之后，我们将得到一个替代的划分序列。

那么，我们在这里干什么呢？

• 与原始Hoare方案一样，首先我们从左侧扫描并找到这样的值“A[i]>=p”，它应该位于右侧。但是，我们没有用其他值交换它，而是记住它：“tmp:=A[i]”。
• 接下来，我们从右侧扫描，找到这样的值“A[j]<p”，它应该位于左侧。我们只需执行赋值“A[i]:=A[j]”，而不会丢失“A[i]”的值，因为它已经存储在“tmp”中。
• 接下来，我们从左侧继续扫描，找到这样的值“A[i]>=p”，它也应该转到右侧。因此，我们进行赋值“A[j]：=A[i]”，而不会丢失值“A[j]”，因为它已经被赋值给了'i'的前一个位置。
• 这种模式继续下去，一旦索引i和j相遇，仍然需要将大于'p'的值放置在“A[j]”中，我们只需执行“A[j]：=tmp”，因为最初变量“tmp”保存了从左起的第一个值，大于'p’。划分完成。

正如我们所看到的，这里我们只有一个遍历所有“L”值的赋值循环，为了正确地重新排列它们，与Hoare方案的“3*L/2”赋值相比，只需要“L+1”值赋值。

我更喜欢将这种新的划分方案称为“循环划分”，因为所有应该以某种方式重新排列的“L”值现在都位于一个赋值循环中。

下面给出的是循环划分算法的伪代码。与Hoare方案的伪代码相比，这些变化微不足道，但现在我们将少做1.5倍的任务。

// 通过“循环划分”方案将序列A[0..N）与枢轴值'p'进行划分，
//并返回结果右侧部分的第一个值的索引。
function partition_cyclic( A[0..N) : Array of Integers, p: Integer ) : Integer
 i := 0
 j := N-1
 // 找到左边第一个不在其位置的值
 while i < N and A[i] < p
 i := i+1
 if i == N
 return N // 所有N值都移到左侧
 //下面开始循环赋值
 tmp := A[i] // 唯一一次写向变量'tmp'
 while true
 // 根据需要向右移动索引“j”
 while i < j and A[j] >= p
 j := j-1
 if i == j // 检查扫描是否完成
 break
 //循环中的下一个赋值
 A[i] := A[j]
 i := i+1
 //根据需要向左移动索引“i”
 while i < j and A[i] < p
 i := i+1
 if i == j // 检查扫描是否完成
 break
 // 循环中的下一个赋值
 A[j] := A[i]
 j := j-1
 // 扫描已经完成
 A[j] := tmp // 唯一一次读变量'tmp'
 return j

上面代码中，第5行和第6行设置了两次扫描的开始索引（'i'从左到右，'j'从右到左）。

第7-9行从左侧搜索这样的值“a[i]”，该值应位于右侧。如果事实证明没有这样的值，并且所有N个项目都属于左侧部分，则第10行和第11行会报告这一点并完成算法。

否则，如果找到了这样的值，在第13行，我们会将其记在“tmp”变量中，从而在索引“i”处打开一个空位，用于在那里放置另一个值。

第15-19行从右侧搜索这样的值“a[j]”，该值应移动到左侧。一旦找到，第20-22行将其放入索引“i”处的空位中，之后索引“j”处的位置变为空，并等待另一个值。

同样，第23-27行从左侧搜索这样的值“a[i]”，该值应移动到右侧。一旦找到，第28-30行将其放入索引“j”处的空位中，之后索引“i”处的位置再次变空，并等待另一个值。

这种模式在算法的主循环中继续，在第14-30行。

一旦索引'i'和'j'相遇，我们就会在那里有一个空位，第31行和第32行将'tmp'变量中最初记忆的值赋值给那里，因此索引'j'成为第一个保存属于右侧部分的值的索引。

最后一行返回该索引。

这样我们就可以在循环体中一起编写循环的2个赋值，因为正如第3节所证明的那样，“L”总是偶数。

该算法的时间复杂度也是O（N），因为我们仍然从两端扫描序列。它只会减少1.5倍的值赋值，因此加速仅反映在常数因子中。

注意：GitHub网站上提供了C++语言中循环划分的实现，且在本文末尾引文中也有提供。

我还想证明，无论我们使用什么划分方案，Hoare方案中的值“L”都不能降低。假设划分后，左部分的长度为“left _n”，右部分的长度也为“right _n”。现在，如果查看原始未划分数组的左对齐“left_n”长区域，我们会在那里找到一些“t1”值，这些值不在它们的最终位置。因此，这些值大于或等于“p”，无论如何都应该移动到右侧。

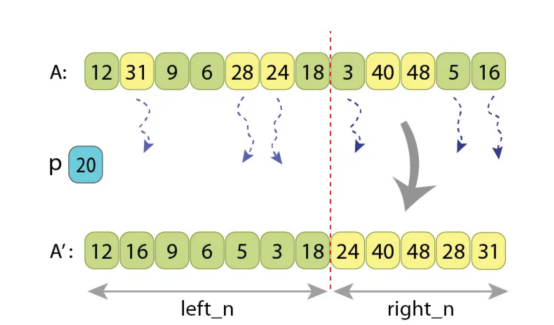划分前后顺序的图示

左侧部分的长度为“left_n=7”，右侧部分的长度是“right_n=5”。

在未划分序列的前7个值中，有“t1=3”

它们大于“p=20”（黄色），应该以某种方式移动到右侧。

在未划分序列的最后5个值中，有“t2=3”

它们小于“p”（浅绿色的），应该以某种方式移动到左侧。

同样，如果查看原始未划分数组的右侧的“right_n”长度范围，我们会在那里找到一些't2'值，这些值也不在它们的最终位置。这些值小于'p'，应该移到左边。我们不能从左向右移动小于“t1”的值，也不能从右向左移动小于“t2”的值。

在Hoare划分方案中，“t1”和“t2”值是相互交换的值。所以我们有：

t1 = t2 = L/2,

或者：

t1 + t2 = L.

这意味着，“L”实际上是应该以某种方式重新排列的最小数量的值，以便对序列进行划分。循环划分算法仅通过“L+1”赋值重新排列它们。这就是我允许自己将这种新的划分方案称为“近乎最优”的原因。

6.实验结果

已经证明，新的划分方案执行的值赋值更少，因此我们可以预期它运行得更快。然而，在发布算法之前，我也想以实验的方式收集结果。

我比较了使用Hoare方案和循环划分进行划分时的运行时间。所有实验都是在随机乱序的数组中进行的。

实验中，使用的不同的参数有：

• N——数组的长度，
• “left_part_percent”——划分后左部分长度的百分比（N时）
• 在原始数据类型变量（32位整数）的数组上运行，与在某种大型对象的数组（256个16位整数的长静态数组）上运行相比。我想澄清为什么我发现有必要在原始数据类型的数组和大型对象的数组上运行划分。在这里，我所说的“大对象”是指与原始数据类型相比占用更多内存的值。在对原始数据类型进行划分时，将一个变量分配给另一个变量的速度将与这两种算法中使用的几乎所有其他指令一样快（例如递增索引或检查循环条件）。同时，在对大型对象进行划分时，与其他使用的指令相比，将一个这样的对象分配给另一个对象将花费更多的时间，而此时我们有兴趣尽可能减少值赋值的总数。
  我将在本节稍后解释为什么我决定用不同的“left_part_percent”值进行不同的实验。
  实验是在以下系统下使用Google Benchmark性能测试工具进行的：
• CPU：英特尔酷睿i7–11800H@2.30GHz
• 内存：16.0 GB
• 操作系统：Windows 11家庭版，64位
• 编译器：MSVC 2022（/O2/Ob2/MD/GR/Gd）

对原始数据类型的数组进行划分

以下是对原始数据类型（32位整数）的数组运行划分算法的结果：

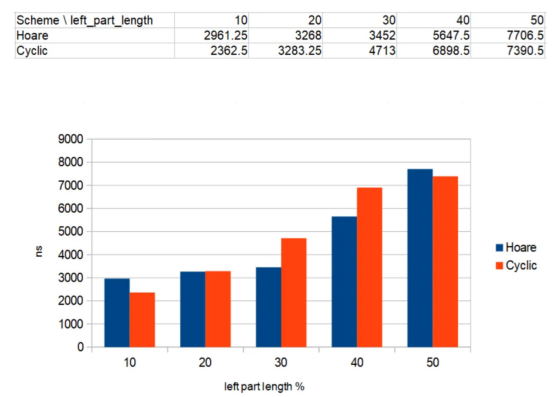在长度为N=10000的32位整数数组上划分算法的运行时间

蓝色条对应于Hoare方案的划分，而红色条对应于循环划分算法。

划分算法针对5种不同的情况运行，基于“left_part_percent”——划分后出现的数组左半部分的百分比（N）。时间以纳秒为单位。

我们观察到，“left_part_percent”的值与两种算法运行时间的相对差异之间没有明显的相关性。这种行为是意料之中的。

对“大型对象”数组进行划分

以下是在所谓的“大对象”数组上运行2个划分算法的结果，每个对象都是一个256长度的16位随机整数静态数组。

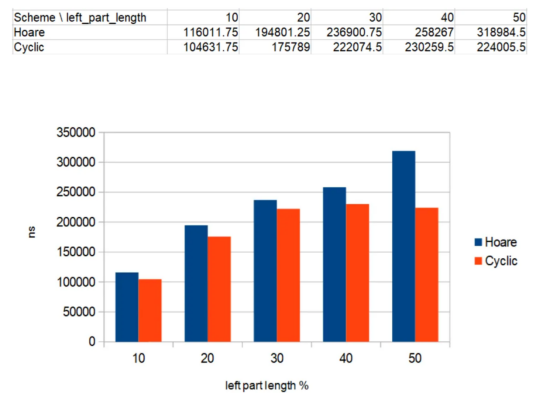
大对象数组上划分算法的运行时间（256个随机16位整数的长静态数组），长度N=10000

其中，蓝色条对应于Hoare方案的划分，而红色条对应于循环划分算法。

划分算法针对5种不同的情况运行，基于“left_part_percent”——划分后出现的数组左半部分的百分比（N）。时间以纳秒为单位。

现在，我们看到了一个明显的相关性：循环划分比Hoare方案表现得更好，因为“left_part_percent”接近50%。换句话说，当划分后数组的左右部分看起来长度更近时，循环划分的工作速度相对更快。这也是一种预期的行为。

实验结果说明

第一个问题：为什么当“left_part_percent”接近50%时，划分通常需要更长的时间呢？

让我们想象一下一个极端情况——划分后几乎所有值都出现在左（或右）部分。这意味着，数组的几乎所有值都小于（或大于）基准值。这意味着，在扫描过程中，所有这些值都被认为已经处于最终位置，并且执行的值赋值很少。如果试着想象另一种情况——当划分后左右部分的长度几乎相等时，这意味着执行了大量的值赋值（因为最初所有值在数组中都是随机混洗的）。

第二个问题：在查看“大型对象”的划分时，为什么当“left_part_percent”接近50%时，两种算法的运行时间差异会变得更大？

前面的解释表明，当“left_part_percent”接近50%时，需要在数组中进行更多的值赋值。在前面的几节中，我们还表明，与Hoare方案相比，循环划分总是使值赋值减少1.5倍。因此，当我们通常需要对数组中的值进行更多重新排列时，1.5倍的差异对整体运行时间的影响更大。

第三个问题：为什么对“大对象”进行划分时的绝对时间（以纳秒为单位）比对32位整数进行划分时大？

这个方法很简单——因为将一个“大对象”分配给另一个对象比将一个原始数据类型分配给其他类型需要更多的时间。

此外，我还对不同长度的数组进行了所有实验，但总体情况没有改变。

7.结论

在本文中，我介绍了一种经过修改的划分方案，称为“循环划分”。与目前使用的Hoare划分方案相比，它总是能够减少1.5倍的值赋值。

当然，在对序列进行划分时，值赋值并不是唯一执行的操作类型。除此之外，划分算法检查输入序列“A”的值是否小于或大于基准值“p”，以及它们对“A”上的索引进行递增和递减。比较、增量和减量的数量不会受到引入“循环划分”的影响，因此我们不能指望它的运行速度快1.5倍。然而，当对复杂数据类型的数组进行划分时，其中值赋值比简单地递增或递减索引要耗时得多，整个算法的运行速度实际上可以快1.5倍。

划分过程是快速排序算法的主要程序，也是查找未排序数组中值或查找其k阶统计量的算法的主要例程。因此，在处理复杂数据类型时，我们还可以预期这些算法的性能提高1.5倍。

除非另有说明，本文中所有使用的图像均按作者本人要求而设计。

参考文献

【1】——C++中循环划分的实现：https://github.com/tigranh/cyclic_partition。

译者介绍

朱先忠，51CTO社区编辑，51CTO专家博客、讲师，潍坊一所高校计算机教师，自由编程界老兵一枚。

原文标题：Cyclic Partition: An Up to 1.5x Faster Partitioning Algorithm，作者：Tigran Hayrapetyan