大家好,我是小寒
今天给大家分享机器学习中的一个关键概念,交叉验证
交叉验证是机器学习中用于评估模型泛化能力的一种方法,用于衡量模型在训练集之外的新数据上的表现。
它的核心思想是将数据集划分为多个子集,模型在不同的子集上交替进行训练和测试,从而减少模型在某一特定数据分割上的偏差。交叉验证能够有效地降低模型过拟合的风险,从而提高模型评估的稳定性和可靠性。
交叉验证的作用
- 提升模型稳定性
通过在不同数据组合上测试模型,可以减少由于数据集单一划分引起的偏差。 - 防止过拟合
在多个验证集上验证模型,可以有效评估模型在新数据上的表现,从而降低过拟合的风险。 - 更客观的评估
交叉验证提供了一种系统性、可重复的方法,使模型评估更为准确和客观。
交叉验证的工作流程
- 数据划分
将数据集随机划分为多个子集(通常称为“折”)。 - 循环训练和验证
在每次循环中,选择一个子集作为验证集,剩下的子集作为训练集,用训练集训练模型,然后在验证集上测试模型的性能。 - 计算平均性能
每次验证的结果都记录下来,最后对这些结果求平均值,得到模型的总体性能评估。
常见的交叉验证方法
1.K 折交叉验证方法
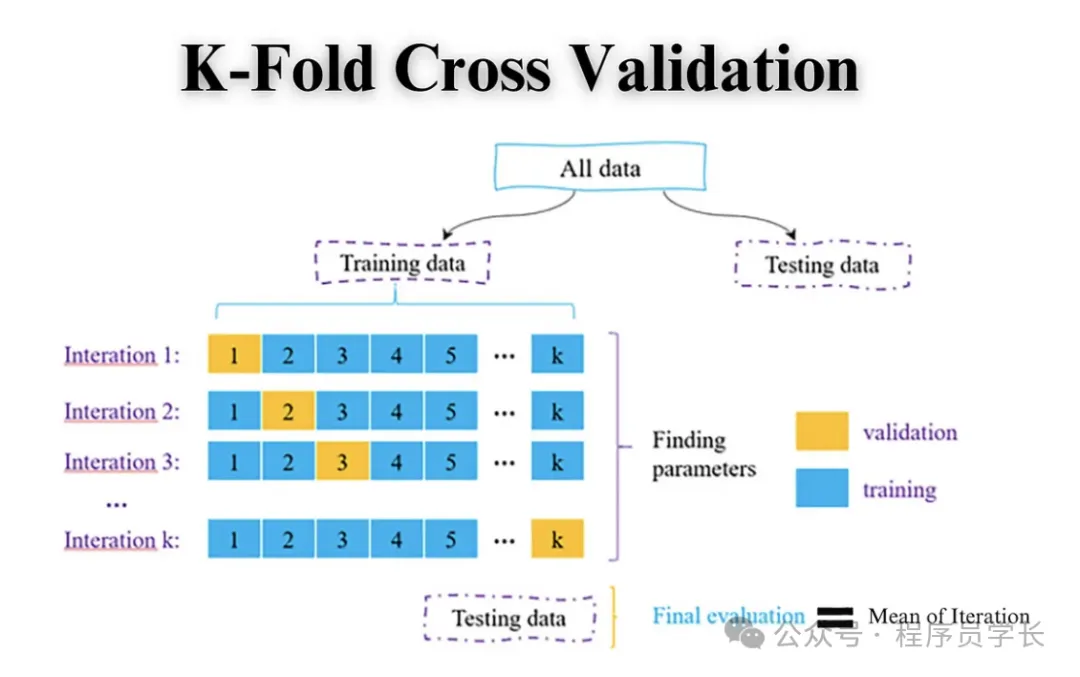
K 折交叉验证将数据集分成 K 个不重叠的子集(折),每次将其中一个子集(折)作为测试集,其余 K-1 个折作为训练集。
重复这个过程 K 次,每次用不同的折作为测试集,最终将 K 次测试的结果平均,以得到模型的总体性能。
 图片
图片
优点
- 每个数据点都能作为测试集的一部分,且每个折都被用于训练和测试。
- 适合数据量较小的情况。
缺点
- 计算开销较大,特别是当 K 较大时。
- 对于时间序列等具有时间依赖性的数据,不适用。
from sklearn.model_selection import KFold, cross_val_score
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
# 加载数据
data = load_iris()
X, y = data.data, data.target
# 设置K折交叉验证
kf = KFold(n_splits=5)
model = RandomForestClassifier()
# 使用交叉验证评分
scores = cross_val_score(model, X, y, cv=kf)
print("K-Fold Cross-Validation Scores:", scores)
print("Mean Score:", scores.mean())2.留一交叉验证
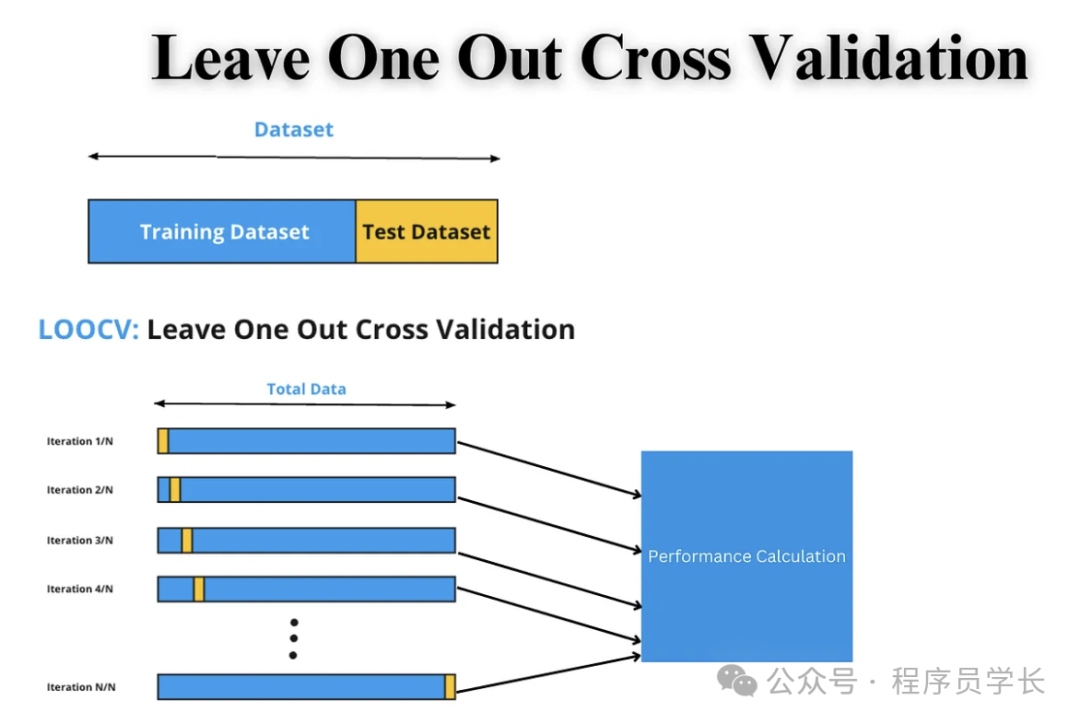
留一交叉验证是 K 折交叉验证的极端形式,其中 K 等于样本总数 N。
每次选取一个样本作为测试集,其余 N-1 个样本作为训练集,重复该过程 N 次,最后计算平均误差。
 图片
图片
优点
- 使用了几乎所有的数据进行训练,模型训练效果较好。
- 适合数据集极小的情况。
缺点
- 计算成本高,特别是当数据量很大时。
- 当数据包含噪声时,结果容易受到单个异常值的影响。
from sklearn.model_selection import LeaveOneOut
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
# 加载数据
data = load_iris()
X, y = data.data, data.target
# 设置留一交叉验证
loo = LeaveOneOut()
model = RandomForestClassifier()
# 使用交叉验证评分
scores = cross_val_score(model, X, y, cv=loo)
print("Leave-One-Out Cross-Validation Scores:", scores)
print("Mean Score:", scores.mean())3.引导法
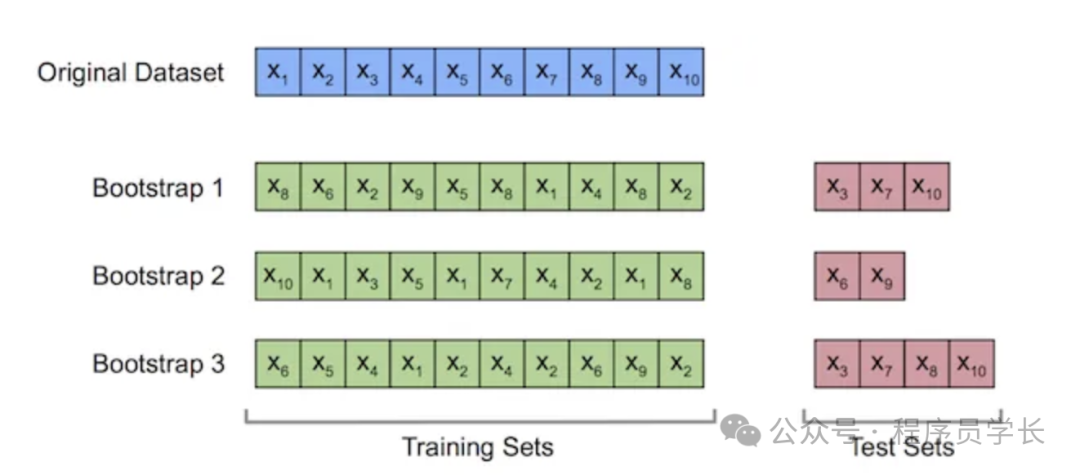
引导法通过有放回地从原始数据集中抽取样本,生成多个子样本(通常与原始数据集大小相同)。
每次从生成的样本中训练模型,未被抽中的样本(称为“包外样本”)作为测试集。
重复该过程多次,并对多次测试结果进行平均。
 图片
图片
优点
- 包外样本可以很好地代表未见数据,从而提供较好的泛化误差估计。
- 数据集中的每个样本有可能在不同的抽样中多次被使用,从而增加数据利用率。
缺点:
- 由于样本是有放回地抽取,导致可能有一些样本被过多地抽取,而有些样本未被抽中。
- 计算复杂度较高。
import numpy as np
from sklearn.utils import resample
from sklearn.metrics import accuracy_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
# 加载数据
data = load_iris()
X, y = data.data, data.target
# 设置引导验证
n_iterations = 100 # 100次引导采样
model = RandomForestClassifier()
bootstrapped_scores = []
for _ in range(n_iterations):
# 使用引导法抽样
X_train, y_train = resample(X, y, replace=True, n_samples=len(y))
X_test = np.array([x for x in X if x.tolist() not in X_train.tolist()])
y_test = np.array([y[i] for i, x in enumerate(X) if x.tolist() not in X_train.tolist()])
# 训练模型并计算准确率
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
score = accuracy_score(y_test, y_pred)
bootstrapped_scores.append(score)
print("Bootstrap Validation Scores:", bootstrapped_scores)
print("Mean Score:", np.mean(bootstrapped_scores))4.嵌套交叉验证
嵌套交叉验证主要用于模型选择和超参数优化。
外层交叉验证用于评估模型的性能,内层交叉验证用于选择模型的最佳超参数。
具体来说,外层将数据分成多个折,每个折作为验证集,剩余部分作为训练集;而在每个外层折的训练集中,又使用内层交叉验证进行超参数搜索。
优点
- 有效防止数据泄漏,是超参数调优的标准方法。
- 提供可靠的模型评估结果,适合用于复杂模型的选择。
缺点
- 计算成本非常高,特别是数据集较大或超参数网格较大时。
from sklearn.model_selection import GridSearchCV, cross_val_score, KFold
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
# 加载数据
data = load_iris()
X, y = data.data, data.target
# 设置参数网格
param_grid = {
'n_estimators': [10, 50, 100],
'max_depth': [3, 5, None]
}
# 设置嵌套交叉验证
outer_cv = KFold(n_splits=5)
inner_cv = KFold(n_splits=3)
# 设置网格搜索和嵌套交叉验证
model = RandomForestClassifier()
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=inner_cv)
nested_scores = cross_val_score(grid_search, X, y, cv=outer_cv)
print("Nested Cross-Validation Scores:", nested_scores)
print("Mean Score:", nested_scores.mean())5.分层交叉验证
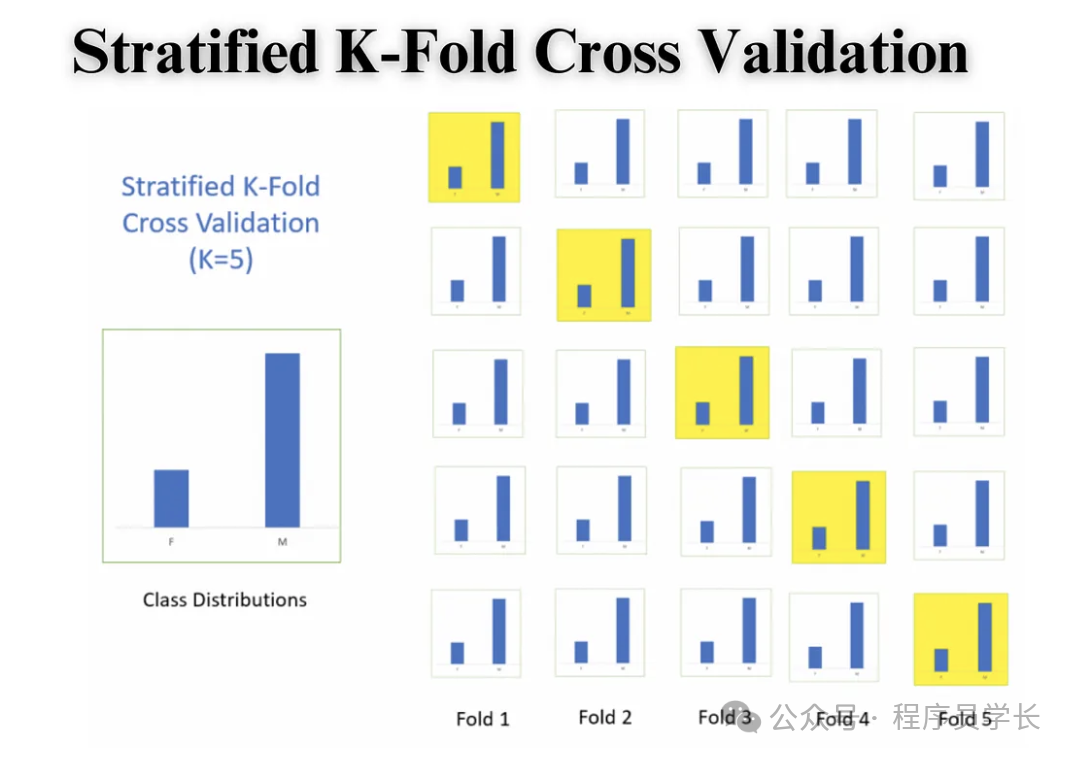
分层交叉验证是一种特殊的交叉验证方法,特别适用于分类任务。
在分层交叉验证中,每个折内的类别分布与整个数据集的类别分布相同,从而在不同折中保持相对一致的标签分布,避免模型评估因为类别失衡而产生偏差。
 图片
图片
优点
- 对于类别不均衡的数据特别有效,能够提供更准确的评估。
- 避免因随机划分导致某些折中类别分布严重偏斜。
缺点
- 仅适用于分类任务,不适用于回归或时间序列任务。
from sklearn.model_selection import StratifiedKFold, cross_val_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
# 加载数据集
data = load_iris()
X, y = data.data, data.target
# 使用分层交叉验证
skf = StratifiedKFold(n_splits=5)
model = RandomForestClassifier()
# 计算交叉验证分数
scores = cross_val_score(model, X, y, cv=skf)
print("Stratified Cross-Validation Scores:", scores)
print("Mean Score:", scores.mean())6.时间序列交叉验证
时间序列交叉验证是一种专门用于时间序列数据的模型评估方法。与传统交叉验证方法(如 K 折交叉验证)不同,时间序列交叉验证遵循时间的自然顺序,从过去到未来逐步划分数据。这种方法适用于时间序列预测任务,能够避免将未来的数据泄漏到模型训练过程中,从而保证模型的真实性能评估。
时间序列交叉验证的常用方法
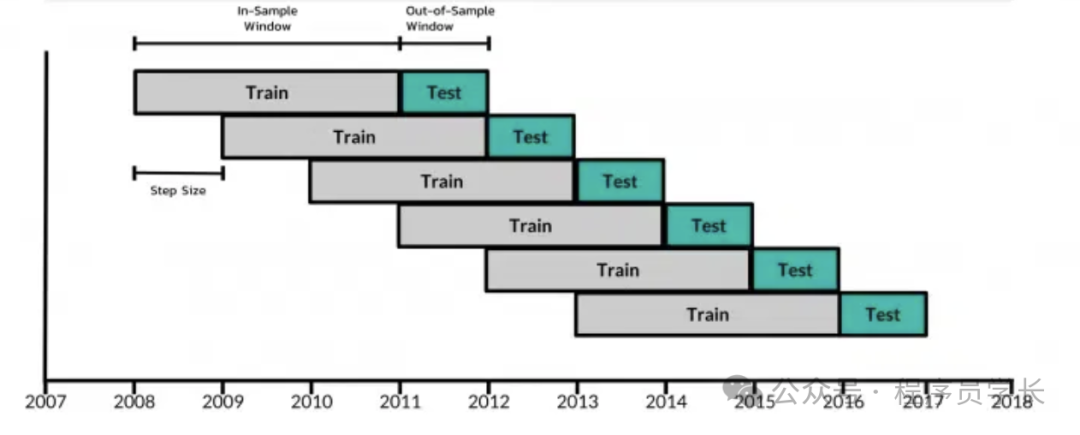
滚动预测法
在滚动预测法中,每次划分训练和测试集时,训练集的大小保持不变,仅在时间上向前滚动。每次只使用最新的训练集数据来预测未来的测试集数据。适合模拟模型实时滚动预测的情况。
 图片
图片
优缺点:
- 优点:模拟真实的预测过程,能更好地反映模型在动态预测中的表现。
- 缺点:每次训练数据有限,模型难以利用更多的历史数据,可能导致不稳定性。
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# 创建时间序列数据
X = np.arange(1, 101).reshape(-1, 1) # 1到100的时间序列
y = X.flatten() + np.random.normal(scale=5, size=X.shape[0]) # 添加噪声
# 定义滚动窗口的大小
window_size = 20 # 每次训练的窗口大小
# 初始化模型
model = LinearRegression()
# 存储预测结果和误差
predictions = []
errors = []
# 滚动窗口法进行预测
for i in range(len(X) - window_size - 1):
# 定义训练集和测试集
X_train = X[i : i + window_size]
y_train = y[i : i + window_size]
X_test = X[i + window_size : i + window_size + 1]
y_test = y[i + window_size : i + window_size + 1]
# 训练模型
model.fit(X_train, y_train)
# 进行预测
y_pred = model.predict(X_test)
# 记录预测和误差
predictions.append(y_pred[0])
mse = mean_squared_error(y_test, y_pred)
errors.append(mse)
print(f"Window {i+1}: Predicted = {y_pred[0]:.2f}, Actual = {y_test[0]:.2f}, MSE = {mse:.2f}")
# 计算平均误差
average_mse = np.mean(errors)
print(f"\nAverage MSE over all windows: {average_mse:.2f}")扩展窗口法
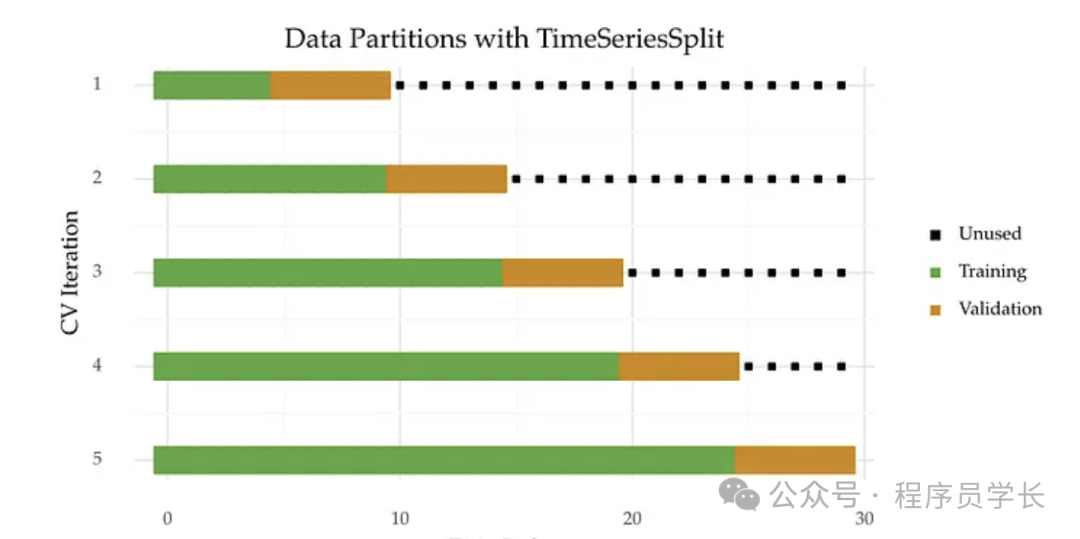
在扩展窗口法中,训练集会随着时间不断扩大,即每次训练时,训练集包含更长时间段的数据,而测试集仍为后续的一小部分数据。这种方法能让模型在预测时利用更多历史数据。
 图片
图片
优缺点
- 优点:通过逐渐扩大训练集,模型可以利用更多的历史信息,提升预测稳定性。
- 缺点:计算开销较大,特别是在训练集不断增大时。
from sklearn.model_selection import TimeSeriesSplit
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import numpy as np
# 创建时间序列数据
X = np.arange(1, 101).reshape(-1, 1)
y = X.flatten() + np.random.normal(scale=5, size=X.shape[0])
# 使用TimeSeriesSplit实现滚动预测法
tscv = TimeSeriesSplit(n_splits=5)
model = LinearRegression()
for train_index, test_index in tscv.split(X):
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print("Test MSE:", mean_squared_error(y_test, y_pred)











































