特征工程是机器学习中的重要步骤之一,其目的是通过对原始数据进行处理、变换或生成新的特征,以增强模型的学习能力和预测性能。


特征工程直接影响机器学习模型的表现,因为模型的效果很大程度上取决于输入数据的质量和特征的选择。
下面,我们来分享10个常用的特征工程技术。
1.插补
插补是处理数据集中的缺失值的一种常用方法。
大多数机器学习算法无法直接处理缺失值,因此在特征工程中必须解决这个问题。
插补方法根据已有的数据推测或生成合理的替代值,以填补缺失的数据。
常见插补方法:
- 均值插补,将缺失值用该特征的均值替代,适用于数值型数据。
- 中位数插补,用中位数替代缺失值,适用于具有异常值的数值数据,因为中位数对极端值不敏感。
- 众数插补,对于类别型数据,使用该特征的众数(最常出现的值)进行插补。
- K近邻插补,基于 K 最近邻算法,用与缺失值最近的 K 个相似样本的平均值进行插补。
- 插值,对时间序列或连续数据,可以使用线性插值或多项式插值方法进行插补。
优缺点
- 插补可以让数据集保持完整,但如果插补策略不当,可能会引入偏差或噪声,影响模型的性能。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import gensim.downloader as api
from gensim.models import Word2Vec
from sklearn.pipeline import Pipeline
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from sklearn.impute import SimpleImputer
from sklearn.compose import ColumnTransformer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.preprocessing import MinMaxScaler, StandardScaler
data = pd.DataFrame({
'doors': [2, np.nan, 2, np.nan, 4],
'topspeed': [100, np.nan, 150, 200, np.nan],
'model': ['Daihatsu', 'Toyota', 'Suzuki', 'BYD','Wuling']
})
doors_imputer = Pipeline(steps=[
('imputer', SimpleImputer(strategy='constant', fill_value=0))
])
topspeed_imputer = Pipeline(steps=[
('imputer', SimpleImputer(strategy='median'))
])
pipeline = ColumnTransformer(
transformers=[
('doors_imputer', doors_imputer, ['doors']),
('topspeed_imputer', topspeed_imputer, ['topspeed'])
],
remainder='passthrough'
)
transformed = pipeline.fit_transform(data)
transformed_df = pd.DataFrame(transformed, columns=['doors', 'topspeed', 'model'])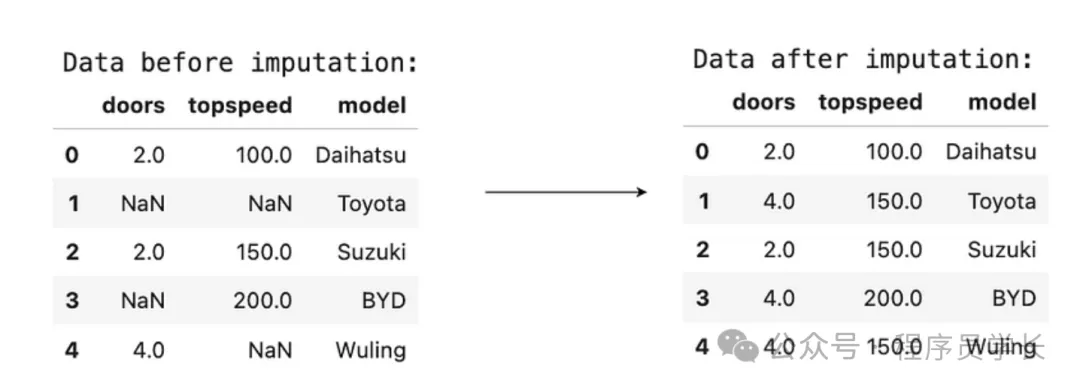
2.分箱
分箱是将连续型数值特征离散化的过程,通过将数值范围划分为多个区间或“箱”,将原始数值转换为离散的类别。
常见的分箱方法
- 等宽分箱,将数值区间按等宽度分成若干个区间,适合均匀分布的数据。
- 等频分箱,将数值按频数分箱,每个箱中的样本数大致相同,适用于不均匀分布的数据。
- 自定义分箱,根据业务逻辑或数据特点,自定义分箱的边界。
应用场景
- 在信用评分等领域,通过分箱处理连续型变量,可以减少数据的噪声,增加模型的稳健性。
np.random.seed(42)
data = pd.DataFrame({'age' : np.random.randint(0, 100, 100)})
data['category'] = pd.cut(data['age'], [0, 2, 11, 18, 65, 101], labels = ['infants', 'children', 'teenagers', 'adults', 'elders'])
print(data)
print(data['category'].value_counts())
data['category'].value_counts().plot(kind='bar')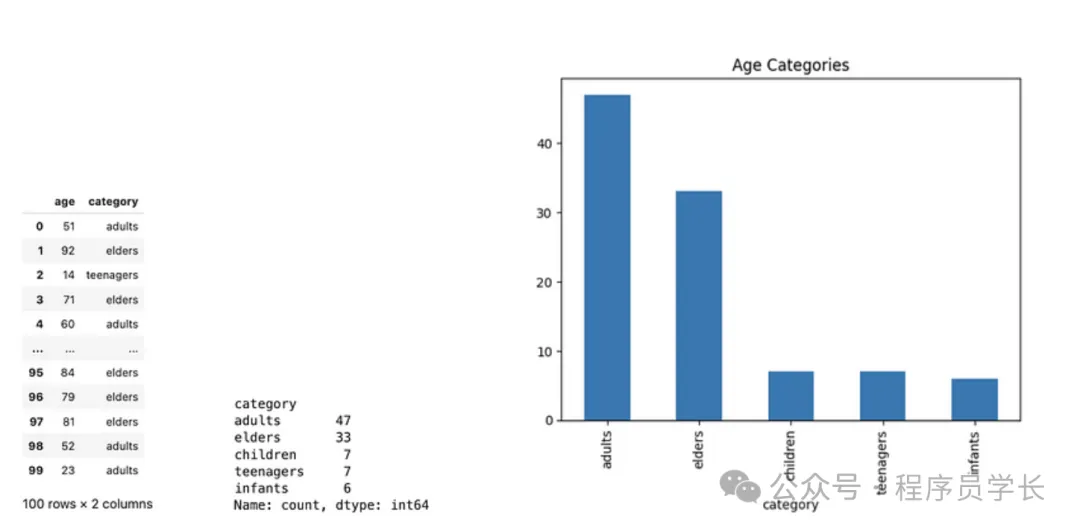
3.对数变换
对数变换是一种数值转换方法,用于处理数据中呈现偏态分布的特征,将其转换为更接近正态分布的数据形式。
对数变换可以减小大值的影响,压缩特征的数值范围。
应用场景
- 处理右偏分布的特征,如收入、价格等数据。
- 适用于减少数据中极大值的影响,避免模型对大值的过度关注。
rskew_data = np.random.exponential(scale=2, size=100)
log_data = np.log(rskew_data)
plt.title('Right Skewed Data')
plt.hist(rskew_data, bins=10)
plt.show()
plt.title('Log Transformed Data')
plt.hist(log_data, bins=20)
plt.show()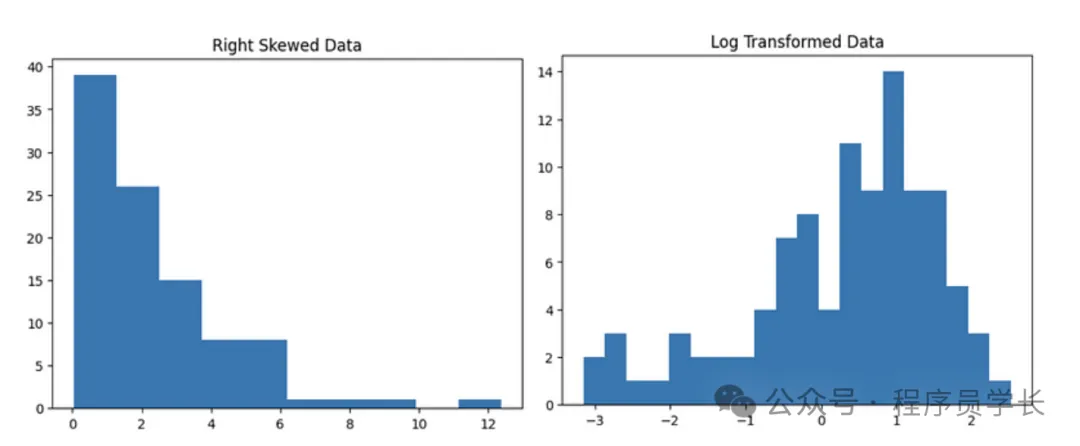
4.缩放
缩放是将特征的数值范围转换到某一固定区间内的过程。
常见的缩放方法
- 标准化将特征值缩放为均值为 0,标准差为1的标准正态分布。公式为:
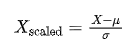
其中,μ是均值,σ是标准差。
- 归一化
将特征缩放到 [0, 1] 范围内。
公式为:
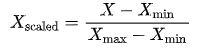
应用场景
- 缩放对于基于距离的算法(如KNN、SVM)和梯度下降优化的算法特别重要,因为特征值的尺度会影响模型的性能。
data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]).reshape(-1, 1)
scaler = MinMaxScaler()
minmax = scaler.fit_transform(data)
scaler = StandardScaler()
standard = scaler.fit_transform(data)
df = pd.DataFrame({'original':data.flatten(),'Min-Max Scaling':minmax.flatten(),'Standard Scaling':standard.flatten()})
df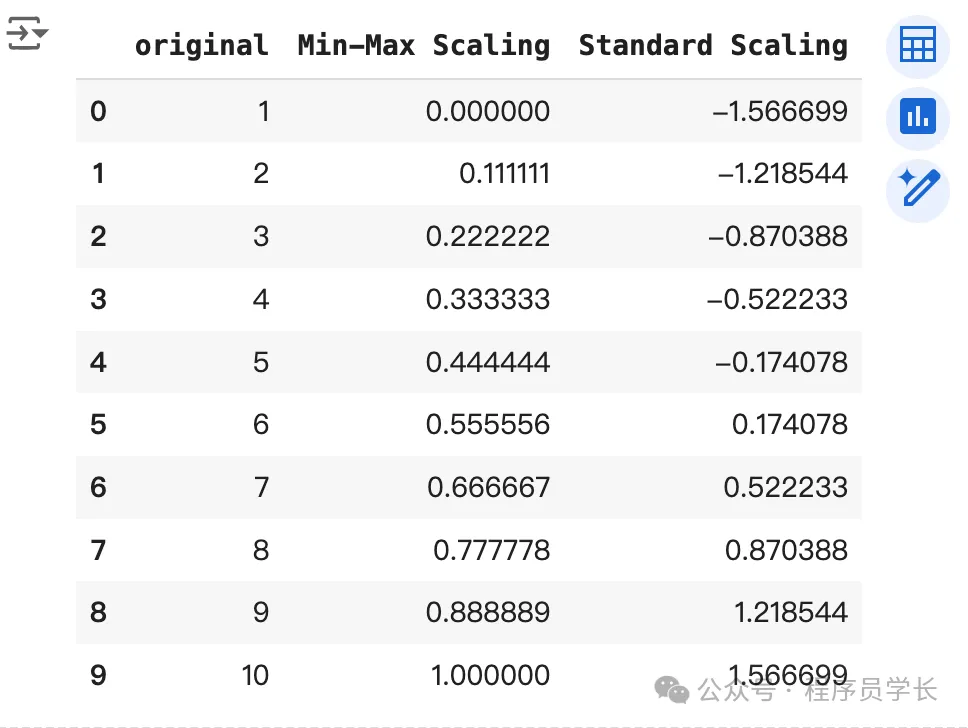
5.独热编码
独热编码是一种将类别型变量转换为二进制特征的编码方式。
每个类别值被转换为一个独立的二进制特征,这些特征值为0或1,表示该样本是否属于对应的类别。
举例
对于类别型特征 “颜色” = {红,蓝,绿},独热编码会将其转换为三个新特征
- 红:1, 0, 0
- 蓝:0, 1, 0
- 绿:0, 0, 1
应用场景
- 独热编码适用于无序的类别型数据,如国家、城市、产品种类等。
- 适用于不具备自然排序关系的特征。
优缺点
- 优点:可以避免类别之间的错误关系,适合没有顺序的分类变量。
- 缺点:当类别数过多时,会导致维度爆炸
data = pd.DataFrame({'models':['toyota','ferrari','byd','lamborghini','honda','tesla'],
'speed':['slow','fast','medium','fast','slow','medium']})
data = pd.concat([data, pd.get_dummies(data['speed'], prefix='speed')],axis=1)
data
6.目标编码
目标编码是一种处理类别型变量的编码方式,通过用该类别与目标变量的统计信息(如均值、概率)来替代类别值。
通常用于高基数的类别变量,避免独热编码导致维度过高的问题。
举例
假设目标是二分类问题,对于类别型特征“城市”,可以用每个城市对应的目标变量均值来替换原始的类别值。
例如,城市A的目标变量均值为0.7,城市B的均值为0.3,城市C的均值为0.5。
应用场景
- 适用于高基数类别型变量(如用户ID、产品ID等),特别是在类别与目标变量有显著关系时。
注意事项
- 为了避免数据泄露(即使用目标值信息),需要对训练集和测试集分别进行编码,或者使用交叉验证技术。
fruits = ['banana','apple','durian','durian','apple','banana']
price = [120,100,110,150,140,160]
data = pd.DataFrame({
'fruit': fruits,
'price': price
})
data['encoded_fruits'] = data.groupby('fruit')['price'].transform('mean')
data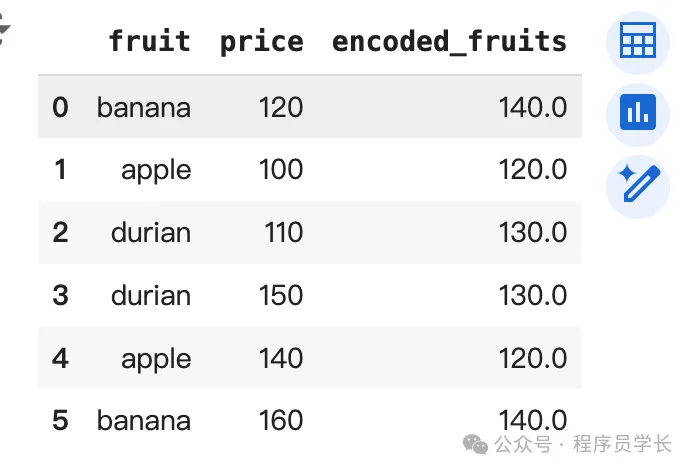
7.主成分分析
PCA 是一种线性降维方法,通过将高维数据投影到一个低维空间,同时尽量保留原始数据的方差信息。
PCA 通过计算数据的协方差矩阵,找到数据的主成分(特征向量),然后选择前几个主成分作为新的特征。
步骤
- 标准化数据。
- 计算协方差矩阵。
- 计算协方差矩阵的特征值和特征向量。
- 根据特征值大小选择前K个特征向量作为主成分。
- 将原始数据投影到新的主成分上。
应用场景
- PCA常用于高维数据集的降维,如图像、基因数据,目的是减少特征数量,降低计算复杂度,同时保留最重要的信息。
iris_data = load_iris()
features = iris_data.data
targets = iris_data.target
pca = PCA(n_compnotallow=2)
pca_features = pca.fit_transform(features)
for point in set(targets):
plt.scatter(pca_features[targets == point, 0], pca_features[targets == point,1], label=iris_data.target_names[point])
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.title('PCA on Iris Dataset')
plt.legend()
plt.show()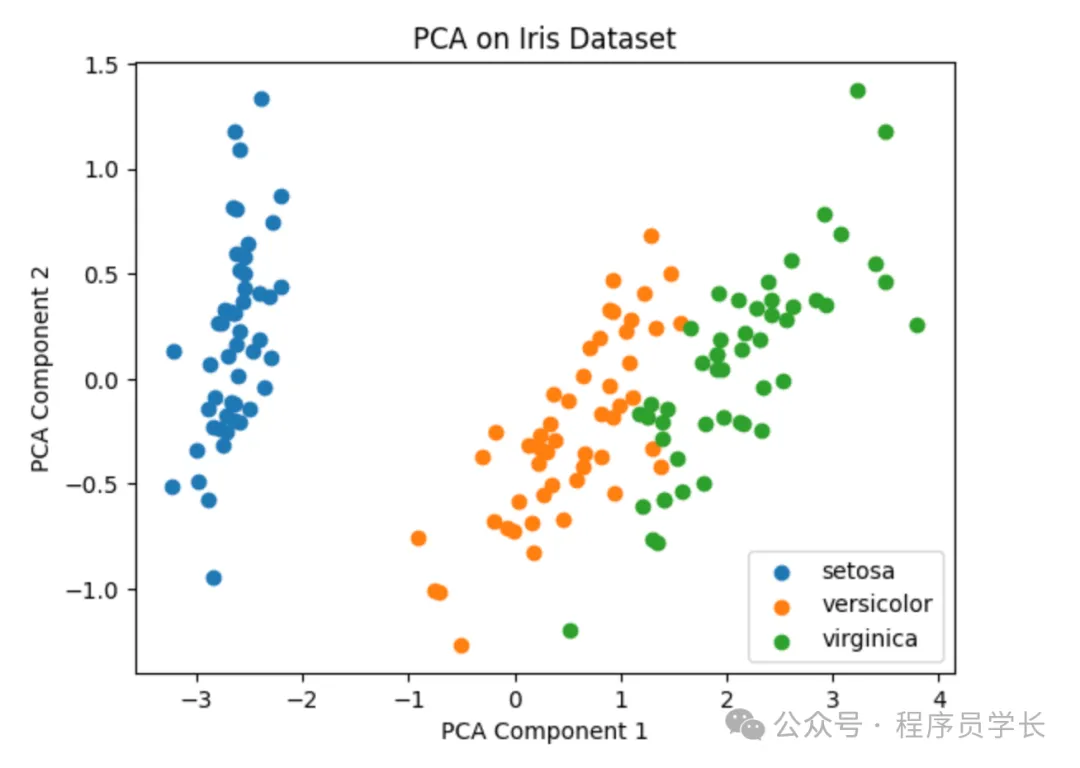
8.特征聚合
特征聚合是一种通过聚合现有特征来生成新特征的技术。
聚合可以通过多种方式实现,如计算平均值、总和、最大值、最小值等。
特征聚合特别适合处理时间序列数据或分组数据。
应用场景
- 在时间序列数据中,可以对某一特征在多个时间窗口上计算统计量,如移动平均、累计总和等。
- 在分组数据中,可以对每个用户的购买记录进行聚合,生成新的特征(如总购买金额、平均购买频率等)。
quarter = ['Q1','Q2','Q3','Q4']
car_sales = [10000,9850,13000,20000]
motorbike_sales = [14000,18000,9000,11000]
sparepart_sales = [5000, 7000,3000, 10000]
data = pd.DataFrame({'car':car_sales,
'motorbike':motorbike_sales,
'sparepart':sparepart_sales}, index=quarter)
data['avg_sales'] = data[['car','motorbike','sparepart']].mean(axis=1).astype(int)
data['total_sales'] = data[['car','motorbike','sparepart']].sum(axis=1).astype(int)
data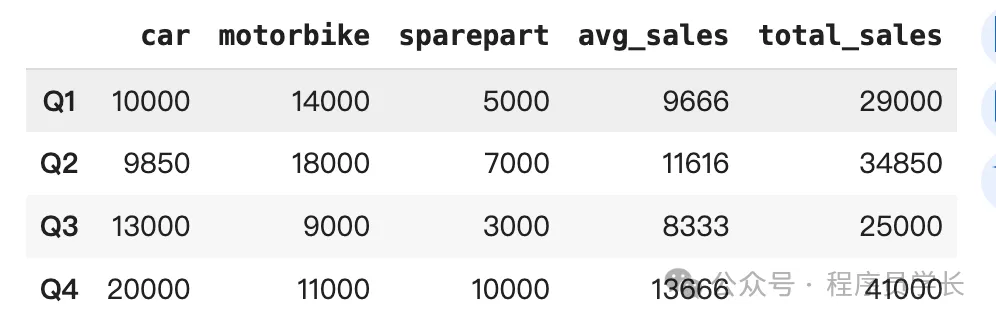
9.TF-IDF
TF-IDF 是一种衡量文本中词汇重要性的特征工程技术,广泛应用于自然语言处理(NLP)任务。
它通过计算词频(TF)和逆文档频率(IDF)来评估某个词在文本中的重要性:
- 词频(TF),某个词在文档中出现的频率。
- 逆文档频率(IDF),表示词在所有文档中出现的稀有程度,常见词会被削弱。
TF-IDF 公式:
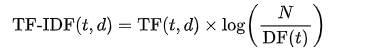
其中 N 是文档总数, 是词 t 出现在多少个文档中的次数。
texts = ["I eat rice with eggs.",
"I also love to eat fried rice. Rice is the most delicious food in the world"]
vectorizer = TfidfVectorizer()
tfidfmatrix = vectorizer.fit_transform(texts)
features = vectorizer.get_feature_names_out()
data = pd.DataFrame(tfidfmatrix.toarray(), columns=features)
print("TF-IDF matrix")
data
10.文本嵌入
文本嵌入是将文本数据转化为数值向量的技术,目的是将语义信息保留在低维向量空间中,使其能够被机器学习模型处理。
常见的文本嵌入方法有:
- Word2Vec,将词映射为向量,类似语义的词会在向量空间中更接近。
- GloVe,基于共现矩阵生成词向量,保持词语之间的全局关系。
- BERT,上下文感知的词向量模型,能够捕捉词在不同上下文中的含义。
文本嵌入可以捕捉文本中的语义信息,使模型能够理解文本间的关系。
corpus = api.load('text8')
model = Word2Vec(corpus)
dog = model.wv['dog']
print("Embedding vector for 'dog':\n", dog)












































