近年来,大语言模型已经在多种任务上表现出来出色的能力,然而,由于缺乏事实性信息,当前的LLM经常出现严重的幻觉现象;此外,LLM中的知识是通过其参数进行编码记忆,这意味着要融入新知识需要进一步的微调,消耗大量的时间与计算资源。因此,通过结合外部检索器来增强LLM的性能,已经成为了主流的方案。
尽管RAG在现代LLM中被广泛采用,但对于RAG如何辅助推理的深入理解仍然是一个未解的问题。目前,大多数研究人员主要将RAG视为提供领域特定知识的方法,并常常试图通过RAG使LLM适应特定子领域。然而,RAG在增强推理能力方面的影响尚未得到深入研究。
近日,来自中国人民大学的学者指出,RAG可以帮助LLM提升其推理能力,但其提升有限,并且由于retriever中的噪声,RAG甚至可能造成推理能力的下降。
 图片
图片
论文地址:https://export.arxiv.org/abs/2410.02338
背景与动机
我们可以将LLM视为计算 𝑝(𝑦∣𝑞),其中q 代表问题query,𝑦是相应的答案。
在这种情况下,检索增强生成(RAG)可以表示为 𝑝(𝑦∣𝑞,𝑑1,𝑑2,…,𝑑𝑘),其中 𝑑𝑖 是基于query 𝑞检索到的第 𝑖 个文档。
此外,众所周知的prompt方法「思维链」(CoT)显著增强了LLMs的推理能力,它可以表示为 𝑝(𝑦∣𝑞,𝑥1,𝑥2,…,𝑥𝑘),其中 𝑥𝑖 表示逐步推理的结果。CoT和RAG都旨在将额外的信息融入到输入中,以获得更好的性能。理论上和实验上都已证明,CoT能够有效提升LLMs的推理能力。那么问题是:RAG是否也能增强LLMs的推理能力?
由于LLM的层数有限,其推理能力局限于固定深度。当将推理路径概念化为一棵树时,其最大深度保持不变。思维链(Chain of Thought, CoT)通过逐步推理或解释来生成答案,而不是直接提供答案,其形式化表达为 𝑥1=𝑓(𝑥), 𝑥2=𝑓(𝑥,𝑥1),…,𝑦=𝑓(𝑥,𝑥1,…,𝑥𝑘)。
这一过程允许CoT通过多次执行𝑓来有效扩展推理深度,随着CoT步骤的增加,潜在地达到无限深度。
相比之下,检索增强生成(RAG)并不支持多次推理;它检索现有的相关信息来生成答案,因此无法堆叠transformer层数。
虽然RAG不能通过堆叠LLM层数来增强推理能力,但检索到的文档可能包含中间推理结果,从而减少了推理所需的层数,使LLM能够处理更复杂的问题,进而帮助提升其推理能力。
树形推理结构
对于一个具有 𝐿层的推理树 𝑇,令第 𝑖 层的节点数量为 𝑛𝑖,并将第 𝑖 层的第 𝑗 个节点表示为 𝑢𝑖,𝑗。检索到的文档 𝑑 包含的相关信息可以用来替换某些推理节点的内容。
例如,考虑query「Who is the actor playing Jason on General Hospital?」。
在这种情况下,可能存在一个节点 𝑢𝑖,𝑗,它表示关于「what is General Hospital?」的信息。如果我们提供一个包含「General Hospital」详细信息的文档,那么 𝑢𝑖,𝑗 的计算就可以通过从该文档中提取相关信息来有效替代。
该文档不仅简化了 𝑢𝑖,𝑗 的计算,还消除了所有仅与 𝑢𝑖,𝑗 相连的节点。这些节点只对 𝑢𝑖,𝑗 的推理有贡献,既然 𝑢𝑖,𝑗 的信息可以直接从文档中得出,那么它们的推理就变得不必要了。因此,检索到与节点 𝑢𝑖,𝑗 相关的单个文档可能会减少多个下层节点的存在。这一过程类似于核武器中的裂变反应,减少一个节点会触发其他多个节点的减少。
因此,如果某一层 𝑙′ 的所有节点都通过检索增强生成(RAG)方法被简化,任何 𝑙≤𝑙′ 的层都可以被消除,从而有效降低整体的推理深度。
 图片
图片
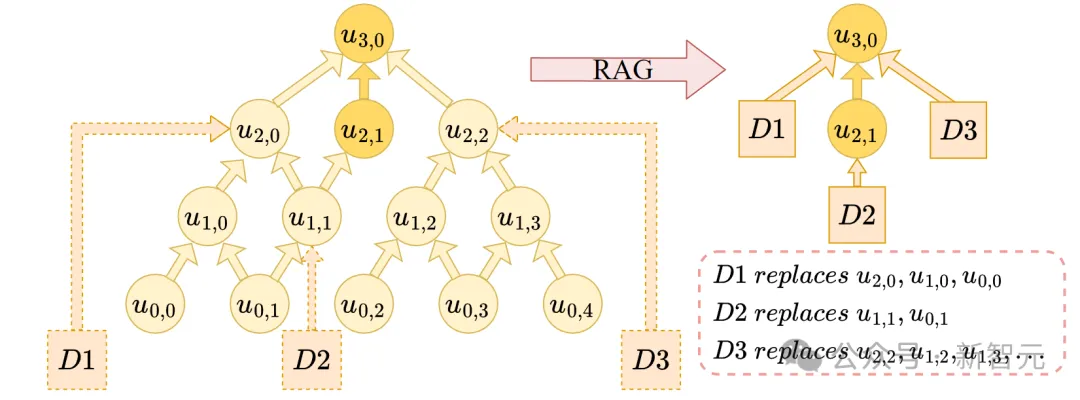
如上图所示,推理树由4层组成,我们检索到了3个文档 𝐷1, 𝐷2, 𝐷3,分别为节点 𝑢2,0、𝑢1,1 和 𝑢2,2 提供了信息。
通过文档 𝐷1,节点 𝑢1,0 也可以被移除,因为它只对 𝑢2,0 有贡献;通过文档 𝐷2,𝑢0,1 也不再需要;由于文档 𝐷3,节点 𝑢1,2 和 𝑢1,3也可以呗移除。
因此,第一层的所有4个节点都可以通过文档信息消除,这意味着第一层和第零层的所有节点都是不必要的。这样,推理深度从4层减少到了2层。因此,借助相关文档,RAG可以有效降低问题的推理复杂度,使LLM能够解决更复杂的问题。
我们可以观察到,消除单个节点会显著影响较浅层中的许多节点,类似于裂变反应。如果这种裂变过程能够无限扩展,RAG可能会大大增强LLMs的推理能力。
然而,如果裂变反应在某个阈值处停止,其效果可能会受到限制。因此,为了评估RAG能够减少多少层,关键在于确定这一类似裂变的过程是否会终止。理解这一动态对于评估RAG如何提升推理能力以及LLMs在复杂问题求解中的整体效率至关重要。
显然,针对第𝑙层,该层节点被erase的概率由两个部分组成,一是由于上层节点的推理不再需要,二是某个文档中包含该节点的信息,假设某个文档中包含该节点的信息的概率为一个常数𝑝
p,并且在第𝑙+1层中有𝑡𝑙+1%被消除,那么第𝑙层节点被消除的概率可以是𝑡𝑙=𝑓(𝑡𝑙+1)=𝑓(𝑡).
令 𝑔(𝑡)=𝑓(𝑡)−𝑡,表示第 𝑙 层的增长,可以考虑在 (0,1) 区间内存在一个点 𝑡^,使得 𝑔(𝑡^)=0。
如果在 𝑡>𝑡^时,𝑔(𝑡)<0,表明被消除的节点数预期会比前一层更少,意味着裂变反应不会无限传播,而是会达到一个临界阈值。超过这一点后,下一层被消除的节点数预计会比当前层减少,从而限制裂变反应的扩展。
 图片
图片
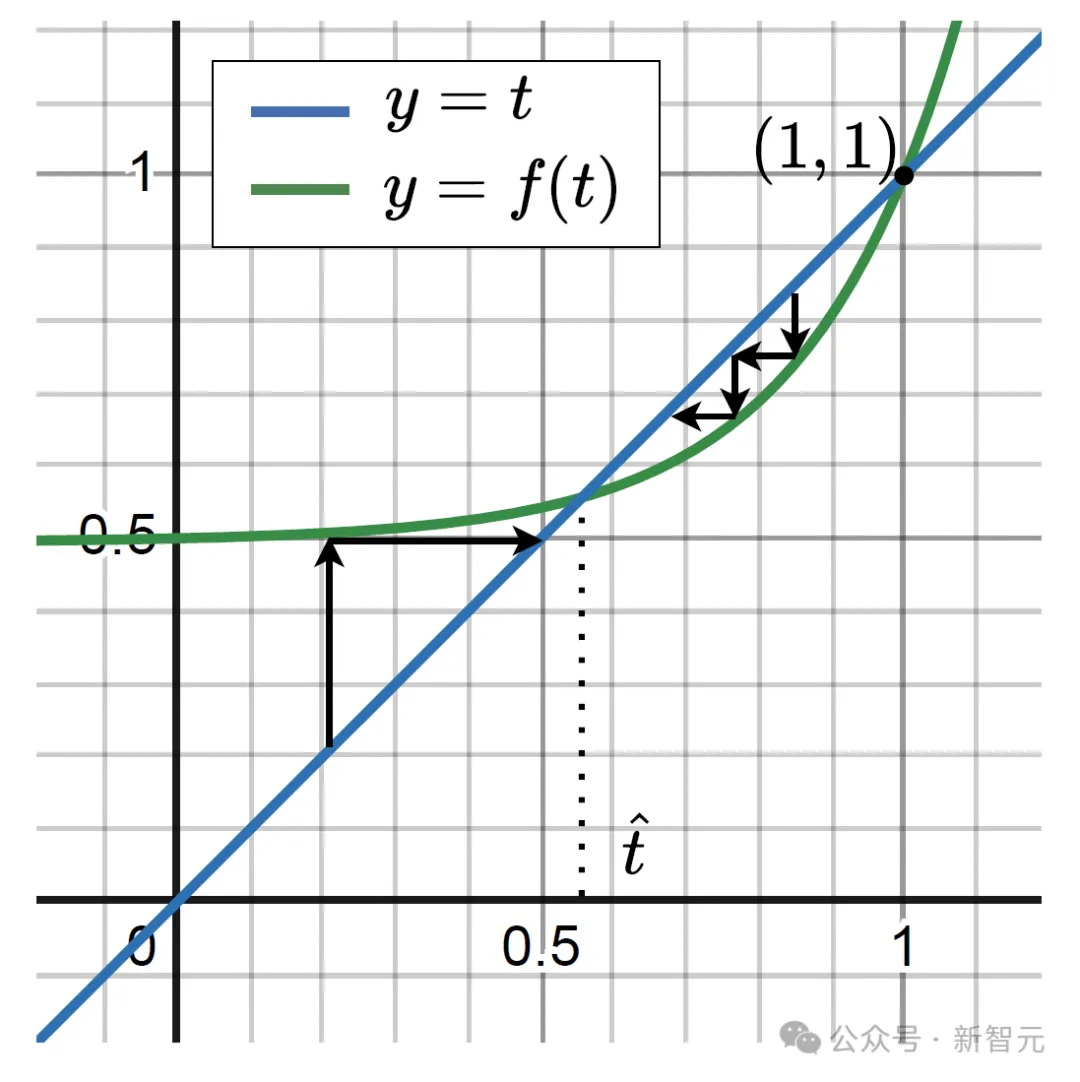
由上图可见,当 𝑡^存在时,节点被erase的概率会逐渐收敛到 𝑡^,无法无限扩张下去,同时 𝑡^的位置取决于层与层之间连接的系数程度和某个文档中包含节点的信息的概率。当层与层之间连接十分稀疏时或者retriever的性能很强,那么就可以使 𝑡^>1,那么节点被erase的概率就会收敛到1,即可erase一整个layer从而降低问题所需的推理深度,使LLM可以解决更复杂的问题。
文档噪声
然而,在实际的RAG场景中,从文档中检索到的信息并不总是可以直接使用,通常需要进一步处理,因为文档可能包含噪声信息,而且有些文档甚至可能包含错误的答案。这些噪声和干扰文档会对性能产生负面影响。
虽然一些研究尝试微调模型以过滤噪声和干扰文档,但该方法使LLM先完成过滤再进行推理,降低了推理能力。此外,一些研究训练另一个过滤模型,但这种方法会导致额外的推理成本,并且无法消除文档中内涵的固有噪声。
因此,出现了一个关键问题:过滤无关文档是否困难,我们能否在有限的层数内有效解决它? 如果过滤噪声所需的成本甚至超过了RAG带来的帮助,那么RAG将无法提升推理能力。
令 𝑟 表示标记的相关性,𝑟𝑖=0 表示标记 第 𝑖个token 𝑥𝑖是噪声,否则该token是相关的。
令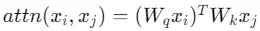 表示LLM的原始注意力层。我们假设期望的自注意力函数为:
表示LLM的原始注意力层。我们假设期望的自注意力函数为:
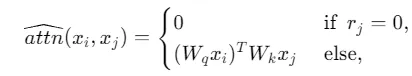 图片
图片
对模型的微调可以表示为
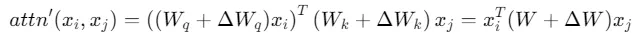 图片
图片
其中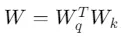 ,ΔW 表示其余项。
,ΔW 表示其余项。
在这种情况下,如果我们需要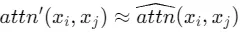 , 我们需要对于所有的相关的token 𝑥𝑗,有
, 我们需要对于所有的相关的token 𝑥𝑗,有
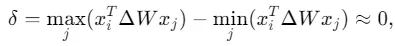
因此,需要对于所有的相关token,有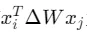 为一个常数,才可以使得
为一个常数,才可以使得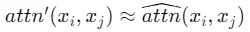 。
。
Triple-Wise Problem
对于输入序列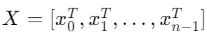 , 𝑟 表示每个token的相关性。
, 𝑟 表示每个token的相关性。
具体来说,对于每个token 𝑥𝑖,相关性得分 𝑟𝑖=0 表示该标记与查询无关。
需要注意的是,计算 𝑟𝑖不仅仅依赖于该token 𝑥𝑖和query;相反,它可能需要涉及三个或更多token。
例如,假设输入为「Alice is exhausted, but Bob is still very excited, showing no signs of fatigue. How does Bob feel?」,单词「exhausted」是一个噪声token,应在推理过程中排除。
然而,确定该token的相关性需要考虑query中的「Bob」以及「exhausted」的主语「Alice」。因此,识别一个标记的相关性需要来自多个token的信息,而自注意力机制仅在成对之间计算关系,这使得在单个transformer层内解决此问题变得困难。
在检索增强生成(RAG)场景中,我们可以简化这个triple wise problem。通过预先计算文档中的信息,并将这些汇总信息表示为一个或几个额外的token(virtual token),我们可以仅使用来自token本身、query和virtual token的信息来评估标记的相关性。在这种情况下,使triple wise problem变为了pair-wise problem。
在判断token 𝑥𝑖是否相关时,不再需要遍历所有的输入token 𝑥𝑗以寻找和query的冲突,仅需遍历所有的virtual token即可。
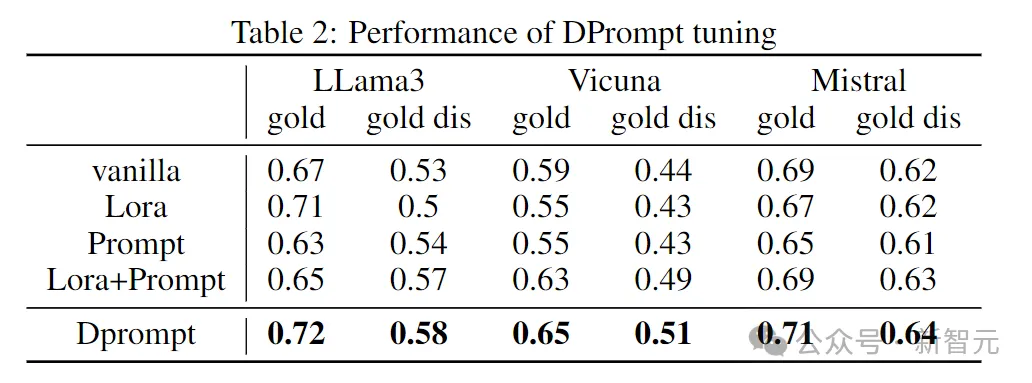
我们微调一个bert模型以获取文档的表征,并通过MLP将其映射到合适的维度,将其作为virtual token插入到模型的输入prompt中进行微调,实验结果如下
 图片
图片
其中gold代表document中只包含一个文档,该文档直接包含了query的答案,但该文档中仍然存在一定的噪声;gold dis代表文档中包含gold文档以及distracting文档,distracting文档中包含错误的答案。由上图可见,DPrompt tuning有效提升了LLM在面对噪声时的性能。
参考资料:
https://arxiv.org/html/2410.02338v2









































