聚类是任何数据科学家必备的技能集,因为它对现实世界问题的实用性和灵活性。本文概述了聚类和不同类型的聚类算法。

什么是聚类?
聚类是一种流行的无监督学习技术,旨在根据对象或观测值之间的相似性将它们分组。聚类有许多有用的应用,如市场细分、推荐系统、探索性分析等。

虽然聚类是数据科学领域众所周知且广泛使用的技术,但有些人可能不了解不同类型的聚类算法。虽然只有少数几种,但理解这些算法及其工作原理对于获得最佳结果至关重要。
基于质心的聚类
当谈到聚类时,大多数人想到的是基于质心的聚类。这是通过使用定义好的质心(中心)数量,根据数据点到每个质心的距离来对数据点进行分组的“传统”方式。质心最终成为其分配的数据点的均值。虽然基于质心的聚类功能强大,但它对异常值不鲁棒,因为异常值需要被分配到某个簇中。
K-Means
K-Means是最广泛使用的聚类算法,很可能是你作为数据科学家首先学习的第一个算法。如上所述,目标是最小化数据点与聚类质心之间的距离之和,以确定每个数据点应该属于的正确组。它的工作原理如下:
- 在未标记数据的向量空间中随机放置定义好的质心数量(初始化)。
- 每个数据点测量自己到每个质心的距离(通常使用欧几里得距离),并将自己分配给最近的质心。
- 质心重新定位到其分配的数据点的均值。
- 重复步骤2-3,直到产生“最优”聚类。

from sklearn.cluster import KMeans
import numpy as np
#sample data
X = np.array([[1, 2], [1, 4], [1, 0],
[10, 2], [10, 4], [10, 0]])
#create k-means model
kmeans = KMeans(n_clusters = 2, random_state = 0, n_init = "auto").fit(X)
#print the results, use to predict, and print centers
kmeans.labels_
kmeans.predict([[0, 0], [12, 3]])
kmeans.cluster_centers_K-Means ++
K-Means ++是对K-Means初始化步骤的改进。由于质心是随机放置的,因此有可能多个质心可能会初始化到同一个聚类中,导致结果不佳。
然而,K-Means ++通过随机分配第一个质心来解决这个问题,这个质心最终将找到最大的聚类。然后,其他质心被放置在初始聚类一定距离之外。K-Means ++的目标是尽可能将质心彼此推得尽可能远。这会产生高质量、独特且定义明确的聚类。
from sklearn.cluster import KMeans
import numpy as np
#sample data
X = np.array([[1, 2], [1, 4], [1, 0],
[10, 2], [10, 4], [10, 0]])
#create k-means model
kmeans = KMeans(n_clusters = 2, random_state = 0, n_init = "k-means++").fit(X)
#print the results, use to predict, and print centers
kmeans.labels_
kmeans.predict([[0, 0], [12, 3]])
kmeans.cluster_centers_基于密度的聚类
基于密度的算法也是一种流行的聚类形式。然而,它们不是从随机放置的质心测量,而是通过识别数据中的高密度区域来创建聚类。基于密度的算法不需要定义聚类的数量,因此优化工作较少。
虽然基于质心的算法在球形聚类中表现更好,但基于密度的算法可以采取任意形状,更加灵活。它们也不将异常值包含在聚类中,因此是鲁棒的。然而,它们可能难以处理密度不一和高维数据。
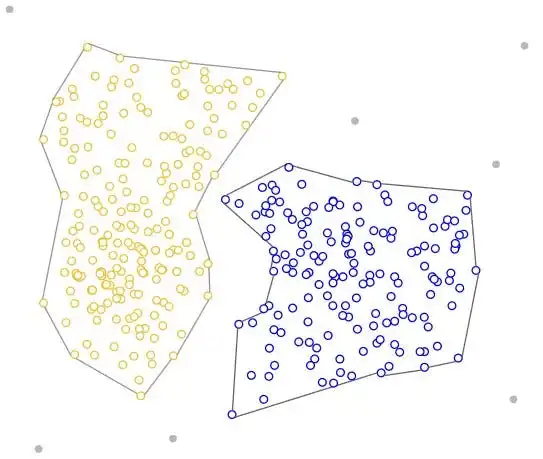
DBSCAN
DBSCAN是最受欢迎的基于密度的算法。DBSCAN的工作原理如下:
- DBSCAN随机选择一个数据点,并检查它在指定半径内是否有足够的邻居。
- 如果该点有足够的邻居,它被标记为聚类的一部分。
- DBSCAN递归检查邻居是否也在半径内有足够的邻居,直到聚类中的所有点都被访问过。
- 重复步骤1-3,直到剩余的数据点在半径内没有足够的邻居。
- 剩余的数据点被标记为异常值。
from sklearn.cluster import DBSCAN
import numpy as np
#sample data
X = np.array([[1, 2], [2, 2], [2, 3],
[8, 7], [8, 8], [25, 80]])
#create model
clustering = DBSCAN(eps=3, min_samples=2).fit(X)
#print results
clustering.labels_层次聚类
接下来,我们有层次聚类。这种方法首先从原始数据计算距离矩阵。这个距离矩阵最好通过树状图(见下文)来可视化。数据点通过找到最近的邻居一个接一个地连接在一起,最终形成一个巨大的聚类。因此,通过停止所有数据点的连接来识别聚类的截止点。
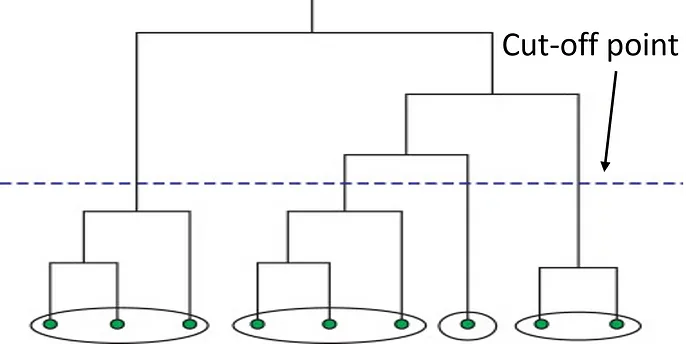
通过使用这种方法,数据科学家可以通过定义异常值并在其他聚类中排除它们来构建一个鲁棒的模型。这种方法非常适合层次数据,如分类学。聚类的数量取决于深度参数,可以从1-n。
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import fcluster
#create distance matrix
linkage_data = linkage(data, method = 'ward', metric = 'euclidean', optimal_ordering = True)
#view dendrogram
dendrogram(linkage_data)
plt.title('Hierarchical Clustering Dendrogram')
plt.xlabel('Data point')
plt.ylabel('Distance')
plt.show()
#assign depth and clusters
clusters = fcluster(linkage_data, 2.5, criterion = 'inconsistent', depth = 5)基于分布的聚类
最后,基于分布的聚类考虑了除距离和密度之外的另一种度量,即概率。基于分布的聚类假设数据由概率分布组成,如正态分布。算法创建代表置信区间的“带”。一个数据点离聚类中心越远,我们就越不确定该数据点属于该聚类。

由于它所做的假设,基于分布的聚类很难实现。除非已经进行了严格的分析来确认其结果,否则通常不建议使用。例如,使用它来识别营销数据集中的客户细分,并确认这些细分遵循分布。这也是一种很好的探索性分析方法,不仅可以了解聚类的中心由什么组成,还可以了解边缘和异常值。
结论
聚类是一种无监督机器学习技术,在许多领域具有日益增长的实用性。它可以用于支持数据分析、细分项目、推荐系统等。在上面,我们已经探讨了它们的工作原理、优缺点、代码示例,甚至一些用例。我认为,由于聚类算法的实用性和灵活性,数据科学家必须具备聚类算法的经验。









































