扩散模型很成功，但也有一块重大短板：采样速度非常慢，生成一个样本往往需要执行成百上千步采样。为此，研究社区已经提出了多种扩展蒸馏（diffusion distillation）技术，包括直接蒸馏、对抗蒸馏、渐进式蒸馏和变分分数蒸馏（VSD）。但是，这些方法也有自己的问题，包括成本高、复杂性高、多样性有限等。
一致性模型（CM）在解决这些问题方面具有巨大的优势。这又进一步分为离散时间 CM 和连续时间 CM。其中离散时间 CM 会引入离散化误差，并且需要仔细调度时间步长网格，这可能会导致样本质量不佳。而连续时间 CM 虽可避免这些问题，但也会有训练不稳定的问题。
近日，OpenAI 的研究科学家路橙（Cheng Lu）与战略探索团队负责人宋飏（Yang Song）发布了一篇研究论文，提出了一些可简化、稳定化和扩展连续时间一致性模型的技术。值得一提的是，这两位作者都是清华校友，师从朱军教授，在扩散概率模型领域做出过代表性工作。
- 论文标题：Simplifying, Stabilizing & Scaling Continuous-Time Consistency Models
- 论文地址：https://arxiv.org/pdf/2410.11081v1
他们的贡献包括：
- TrigFlow，一个将 EDM（arXiv:2206.00364）与流匹配（Flow Matching）统一起来的公式，其能极大简化扩展模型、相关的概率流 ODE 和一致性模型（CM。
- 在此基础上，他们分析了一致性模型训练不稳定的根本原因，并提出了一种完整的缓解方案。他们的方法包括改进网络架构中的时间调节和自适应分组归一化。
- 此外，他们还重新构建了连续时间 CM 的训练目标，其中整合了关键项的自适应加权和归一化以及渐进退火，以实现稳定且可扩展的训练。
简化连续时间一致性模型
作为前提，这里先给出离散时间和连续时间一致性模型的公式：
离散时间 CM：
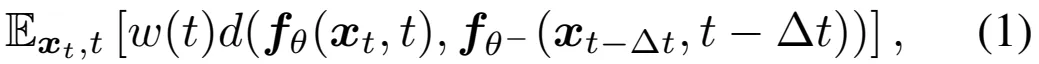
连续时间 CM：
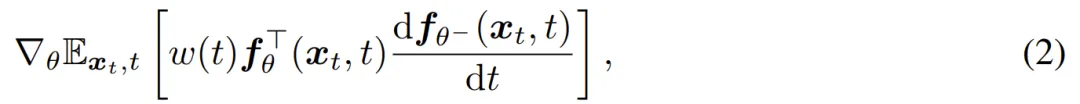
此前的一致性模型采用了 EDM 中的模型参数化和扩散过程。具体来说，一致性模型会被参数化以下形式：
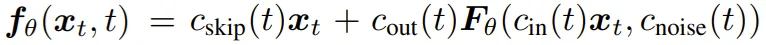
其中，F 是一个神经网络，θ 是其参数；c_skip、c_out、c_in 都是固定的系数，用以确保在所有时间步骤上初始化时扩散目标的方差相等；c_noise 是对 t 的一个变换运算，以便更好地实现时间调节。
由于在 EDM 扩散过程中，方差会爆炸式增长，也就意味着 x_t = x_0 + tz_t，基于此可以推导出下面三式：
虽然这些系数对于训练效率很重要，但由于它们与 t 和 σ_d 之间存在复杂的算术关系，因此会使得对一致性模型的理论分析变得复杂。
为了简化 EDM 及随之的一致性模型，他们提出了 TrigFlow。这种扩散模型形式保留了 EDM 性质，但满足 c_skip (t) = cos (t)、c_out (t) = sin (t)、c_in (t) ≡ 1/σ_d。
TrigFlow 是流匹配（也称为随机插值或整流）和 v 预测参数化的一种特例。它与之前一些研究团队提出的三角插值非常相似，但经过修改从而纳入了对数据分布 p_d 的标准差 σ_d 的考量。
由于 TrigFlow 是流匹配的一个特例，同时满足 EDM 原理，因此其集两者之长，同时还让扩散过程、扩散模型参数化、PF-ODE、扩散训练目标和一致性模型参数化全都变得更简单了。
让连续时间一致性模型变得稳定
连续时间 CM 的训练一直都高度不稳定。因此，它们的表现一直不及之前研究中的离散时间 CM。
为了解决这个问题，该团队在 TrigFlow 框架的基础上，引入了几项基于理论研究的改进措施，其中重点关注的是参数化、网络架构和训练目标。
参数化和网络架构
连续时间 CM 的训练的关键是 (2) 式，其取决于正切函数
，而在 TrigFlow 框架下，该正切函数由以下公式给出：
其中 
表示 PF-ODE，其要么在一致性蒸馏中使用预训练的扩散模型估计得出，要么就在一致性训练中使用从噪声和干净样本计算得到的无偏估计器估计得出。
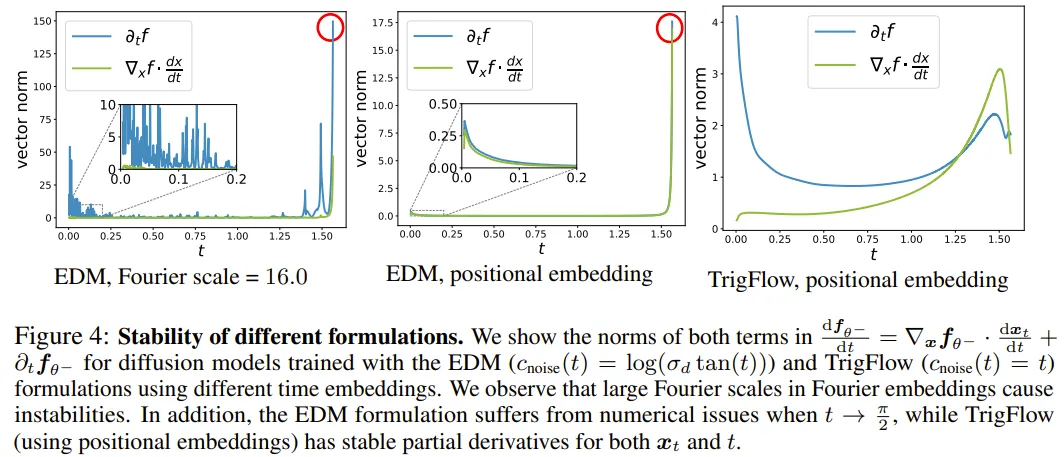
为了让训练过程稳定下来，必须确保 (6) 式中的正切函数在不同时间步骤中保持稳定。该团队在实践中发现 σ_dF_θ、PF-ODE 和噪声样本 x_t 能保持相对稳定。进一步分析后，他们发现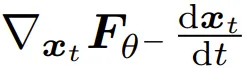
通常经过良好调节。因此不稳定的来源是时间导数 
，而其可被分解为：
其中，emb (・) 是指时间嵌入，通常以位置嵌入或傅里叶嵌入的形式出现在扩散模型和 CM 的相关文献中。
该团队稳定 (7) 中每个元素的方法包括恒等时间变换（c_noise (t) = t）、位置时间嵌入和自适应双重归一化。详见原论文。
图 4 可视化地展示了在 CIFAR-10 上训练 CM 时稳定时间导数的情况。研究表明，这些改进可在不损害扩散模型训练的前提下稳定 CM 的训练动态。
训练目标
使用 TrigFlow 和前述的优化技术，(2) 式中连续时间 CM 训练的梯度就会变为：
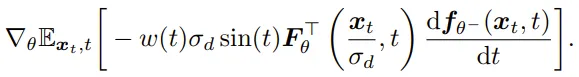
之后，该团队又使用了另外一些技术来显式地控制该梯度，以提升稳定性，其中包括正切归一化、自适应加权、扩散微调和正切预热。详见原论文。
有了这些技术，离散时间和连续时间 CM 训练的稳定性都能得到显著改善。
该团队在相同的设置下训练了连续时间 CM 和离散时间 CM。如图 5 (c) 所示，增加离散时间 CM 中的离散化步骤数 N 可提高样本质量，原因是这样做可减少离散化误差来；但一旦 N 变得太大（N > 1024 之后），样本质量就会降低，这是因为会出现数值精度问题。
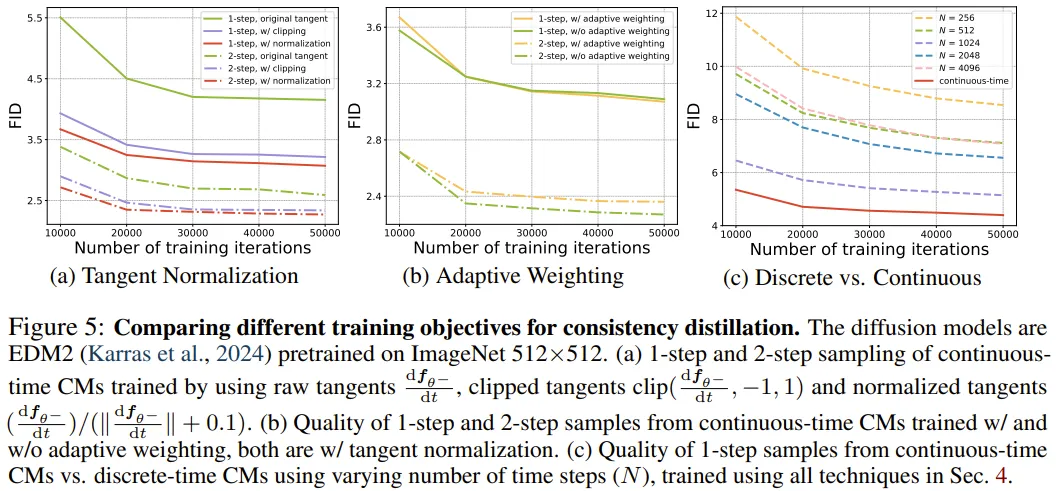
相较之下，在所有 N 值上，连续时间 CM 的表现都显著优于离散时间 CM。这能为我们提供选择连续时间 CM 的强有力依据。
该团队将他们的模型称为 sCM，其中 s 代表 simple、stable、scalable，即简单、稳定和可扩展。下面是 sCM 训练的详细伪代码。
扩展连续时间一致性模型
在这部分，研究者通过在各种具有挑战性的数据集上训练大规模 sCM 来测试上述内容中提出的所有改进措施。
大规模模型中的正切计算
训练大规模扩散模型的常见设置包括使用半精度（FP16）和 Flash Attention。由于训练连续时间 CM 需要精确计算正切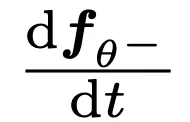 
，我们需要提高数值精度，同时支持高效记忆注意力计算，详情如下。
计算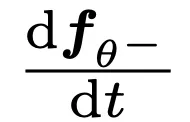
时，需要计算 
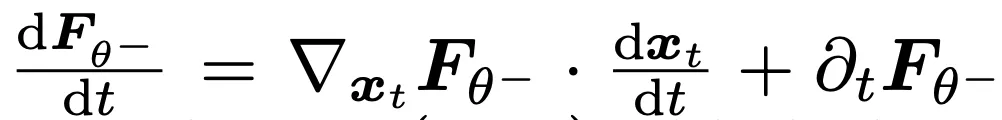，这可通过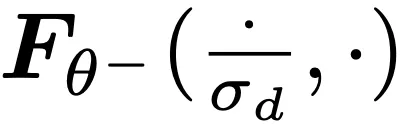
与输入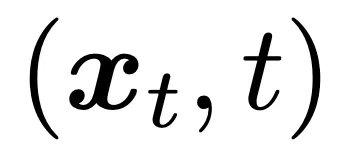向量 
和正切向量 
的雅可比向量积（JVP）高效获得。然而根据经验，当 t 接近 0 或 π/2 时，正切可能会在中间层溢出。为了提高数值精度，研究者认为应该重新安排正切的计算。
具体来说，由于公式 (8) 中的目标函数包含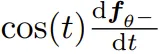
，而 
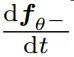与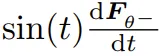 
成正比，因此可以这样计算 JVP：
即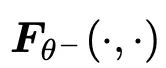
的 JVP，输入为
，正切为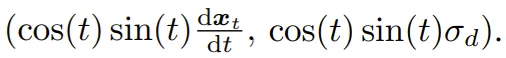
这种重新排列大大缓解了中间层的溢出问题，使 FP16 的训练更加稳定。
Flash Attention 被广泛用于大规模模型训练中的注意力计算，既能节省 GPU 内存，又能加快训练速度。然而，Flash Attention 并不计算雅可比向量积（JVP）。为了填补这一空白，研究者提出了一种类似的算法，它能以 Flash Attention 的风格在一次前向传递中高效计算 softmax 自注意力及其 JVP，从而显著减少注意力层中 JVP 计算所需的 GPU 内存用量。
实验
sCM 的训练计算。研究者在所有数据集上使用与教师扩散模型相同的批大小。sCD 每次训练迭代的有效计算量大约是教师模型的两倍。他们观察到，sCD 的两步采样质量收敛很快，只用了不到教师模型 20% 的训练计算量，就获得了与教师扩散模型相当的结果。在实践中，只需使用 sCD 进行 20k 次微调迭代，就能获得高质量的样本。
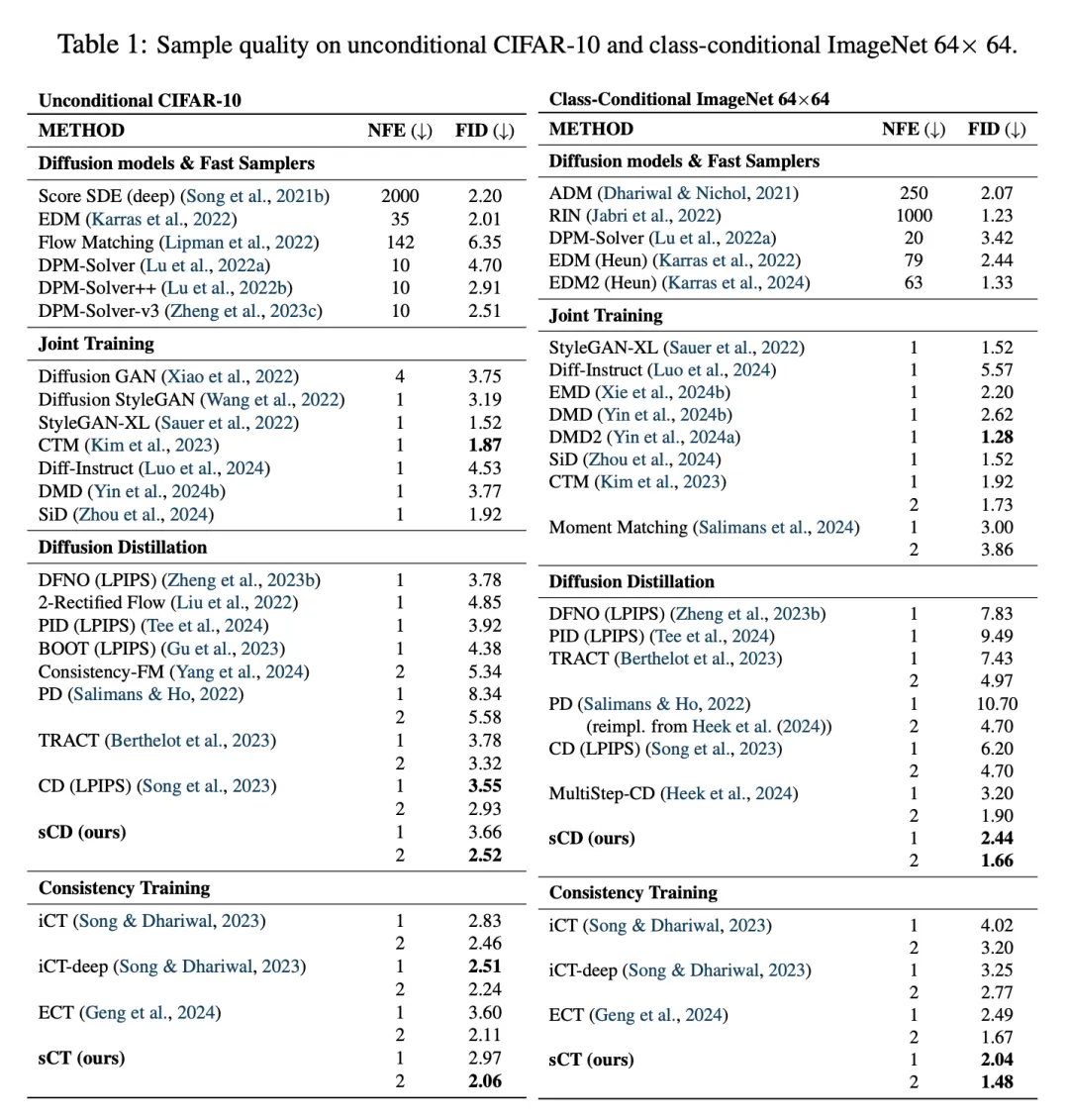
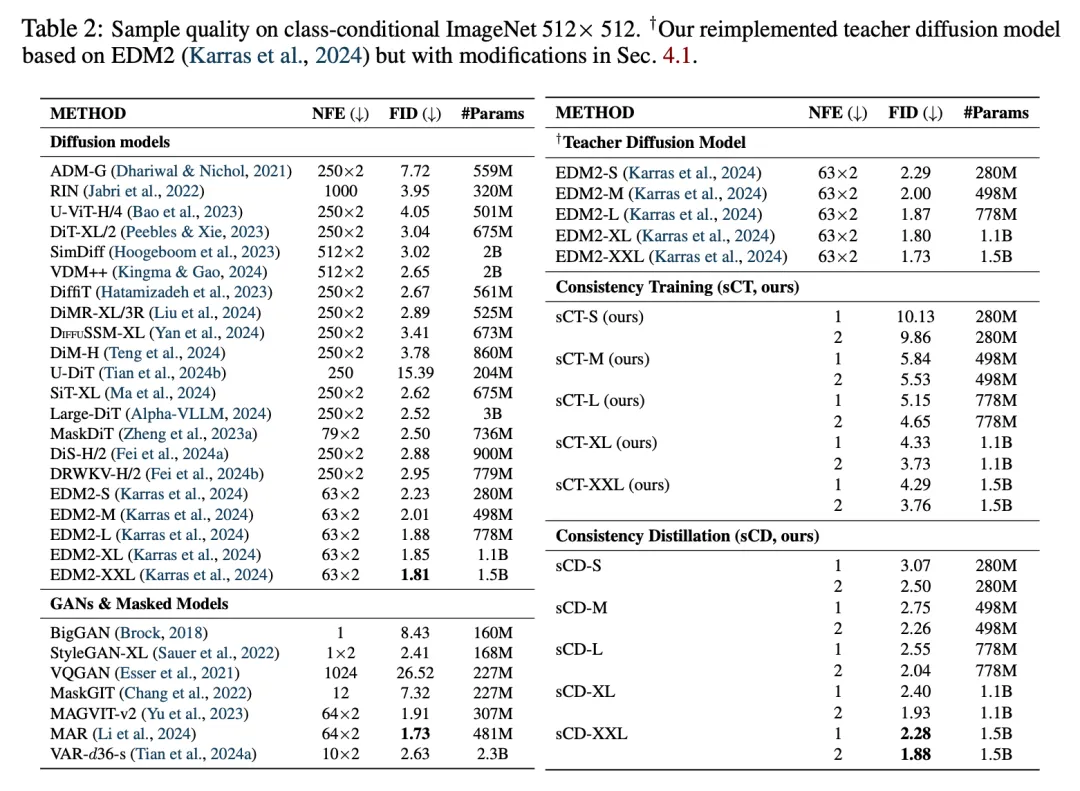
基准。在表 1 和表 2 中，研究者通过 FID 和函数评估次数（NFE）的基准，将本文结果与之前的方法进行了比较。首先，sCM 优于之前所有不依赖与其他网络联合训练的几步式方法，与对抗训练取得的最佳结果相当，甚至超越。值得注意的是，sCD-XXL 在 ImageNet 512×512 上的一步 FID 超过了 StyleGAN-XL 和 VAR。此外，sCD-XXL 的两步 FID 性能优于除扩散模型外的所有生成模型，可与需要 63 个连续步骤的最佳扩散模型相媲美。其次，两步式 sCM 模型将与教师扩散模型的 FID 差距显著缩小到 10% 以内。此外，sCT 在较小的扩展上更有效，但在较大扩展上的方差会增大，而 sCD 在小型扩展和大型扩展上都表现出一致的性能。
Scaling 研究。如图 6 所示，首先，随着模型 FLOPs 的增加，sCT 和 sCD 的样本质量都有所提高，这表明这两种方法都能从 Scaling 中获益。其次，与 sCD 相比，sCT 在较小分辨率下的计算效率更高，但在较大分辨率下的效率较低。第三，对于给定的数据集，sCD 的 Scaling 是可预测的，在不同大小的模型中，FID 的相对差异保持一致。这表明，sCD 的 FID 下降速度与教师扩散模型相同，因此，sCD 与教师扩散模型一样具有可扩展性。随着教师扩散模型的 FID 随规模的扩大而减小，sCD 与教师模型之间 FID 的绝对差异也随之减小。最后，FID 的相对差异随着采样步骤的增加而减小，两步式 sCD 的采样质量与教师扩散模型相当。
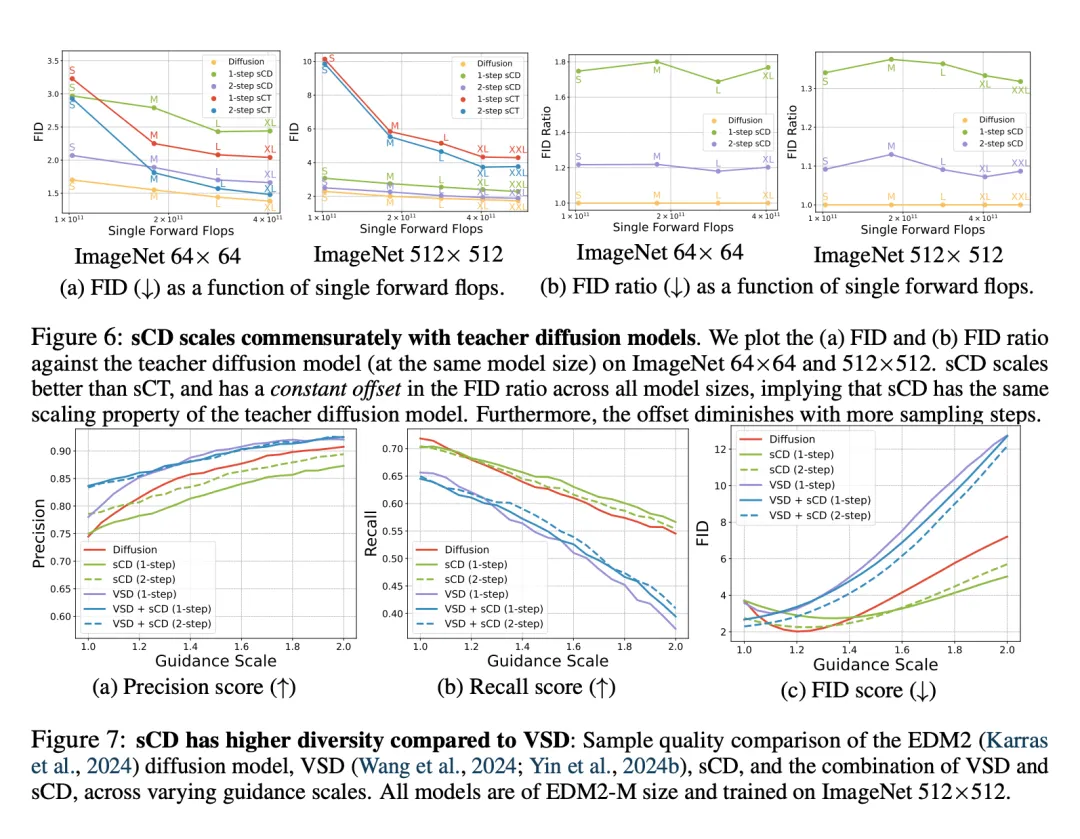
与 VSD 的对比。如图 7 所示，研究者对比了 sCD、VSD、sCD 和 VSD 的组合等（通过简单地将两种损失相加）并观察到，VSD 具有与扩散模型中应用大 guidance scale 类似的人工效应：它提高了保真度（表现为更高的精确度分数），同时降低了多样性（表现为更低的召回分数）。这种效应随着 guidance scale 的增加而变得更加明显，最终导致严重的模式崩溃。相比之下，两步式 sCD 的精确度和召回分数与教师扩散模型相当，因此 FID 分数比 VSD 更高。
更多研究细节，可参考原论文。
