神经网络算法是一种模拟人脑神经元结构和信息处理方式的机器学习模型，其核心思想是通过对输入信息进行分层处理，逐层提取数据特征，进而完成分类、回归等任务。
神经网络算法作为深度学习的基础模型之一，已经在图像识别、自然语言处理、时间序列预测等多个领域取得了显著的成功。
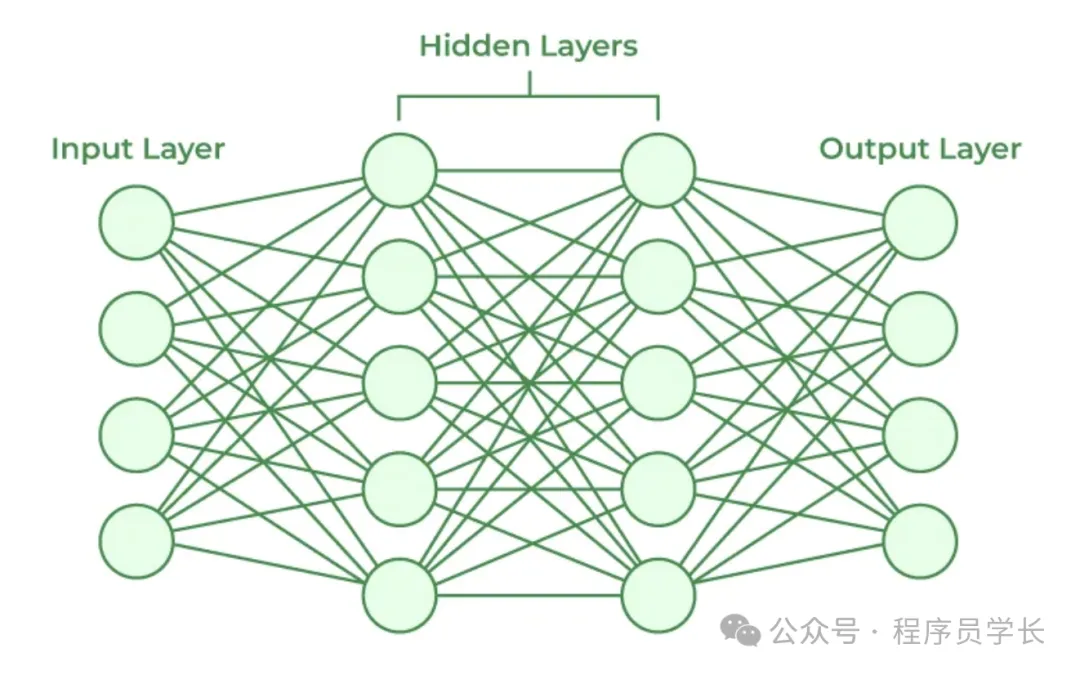
神经网络算法的基本结构
神经网络算法由输入层、隐藏层和输出层组成，每个层包含若干神经元。
- 输入层
输入层负责接收输入数据，每个神经元代表输入数据的一个特征。 - 隐藏层
隐藏层位于输入层和输出层之间，用于对数据进行复杂的非线性转换。
隐藏层的数量和神经元的数量是网络性能的重要参数。 - 输出层
输出层是神经网络的最后一层，它将隐藏层的计算结果转换为最终的输出。
输出层的神经元数量取决于具体任务。对于分类问题，输出层的神经元数量通常等于类别数；对于回归问题，输出层通常只有一个神经元。
神经元的工作原理
每个神经元接收来自上一层的输入值，这些输入值与神经元的权重相乘并累加得到一个加权和。然后，这个加权和通过一个非线性激活函数进行处理，得到该神经元的输出。
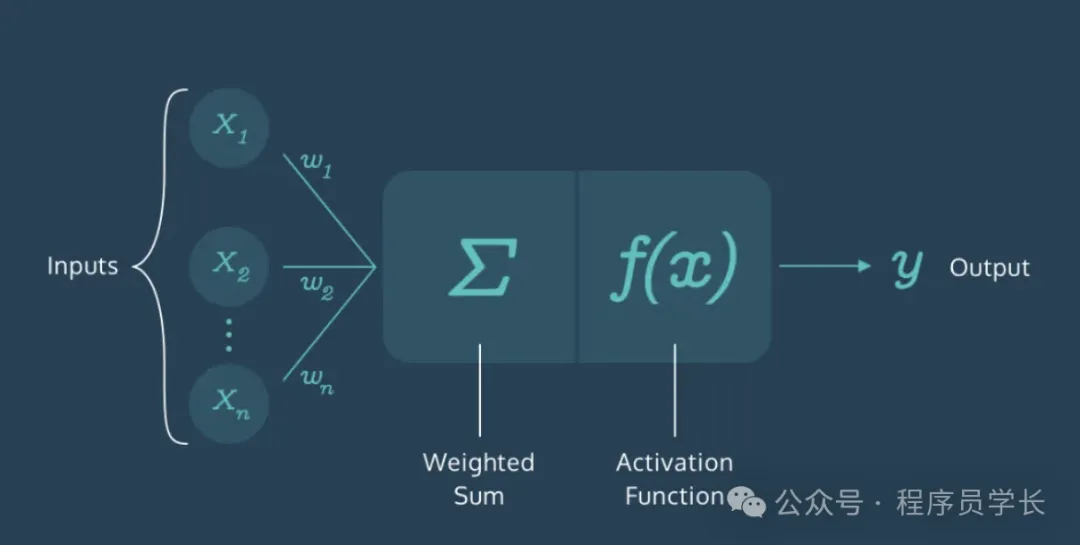
神经元的计算过程可以用以下公式表示：
其中， 是输入， 是对应的权重， 是偏置项， 是加权和。
加权和经过激活函数 后，得到神经元的输出：
激活函数
激活函数用于引入了非线性，从而让神经网络能够处理复杂的非线性关系。
常见的激活函数包括
- Sigmoid
输出范围为 0 到 1，常用于二分类问题。 - Tanh
输出范围为 −1 到 1 - ReLU
输出为正值时保持不变，负值时输出为零。
由于其计算简单且效果较好，ReLU 是最常用的激活函数之一。 - Softmax
常用于多分类问题，用于计算每个类的概率分布。
神经网络的工作过程
神经网络的工作过程可以概括为以下几个关键步骤：前向传播、损失计算、反向传播和权重更新。
通过这些步骤，神经网络从输入数据中学习，并调整权重以提高预测的准确性。
接下来，我们逐步详细解释每一个过程。
前向传播
前向传播是神经网络的预测过程，即从输入数据开始，一层一层地传递计算，最终得到输出结果。
具体步骤
- 输入层
将输入数据直接传递给第一层的神经元，每个输入对应一个神经元。 - 隐藏层计算
对于每一层的神经元，将上一层输出的值与当前层的权重 w 和偏置 b 进行线性组合，然后应用激活函数进行非线性转换。
数学表达为：其中， 是第 l 层的线性组合结果， 是第 l 层的权重矩阵， 是上一层的输出， 是偏置向量。
接下来通过激活函数 进行非线性变换
这里 是第 l 层的输出。 - 输出层计算
当传递到输出层时，网络的最终输出 会根据设计的任务有所不同。
损失函数
损失函数用于衡量神经网络输出（预测值）与实际目标值之间的差异。不同任务通常使用不同的损失函数。
- 对于回归问题，常用的损失函数是均方误差（MSE）其中， 是预测值， 是真实值， 是样本数。
- 对于分类问题，常用的损失函数是交叉熵损失（Cross-Entropy Loss）其中， 是真实标签（0或1）， 是预测概率。
损失函数的输出是一个标量，它代表整个网络对当前数据集的预测误差。
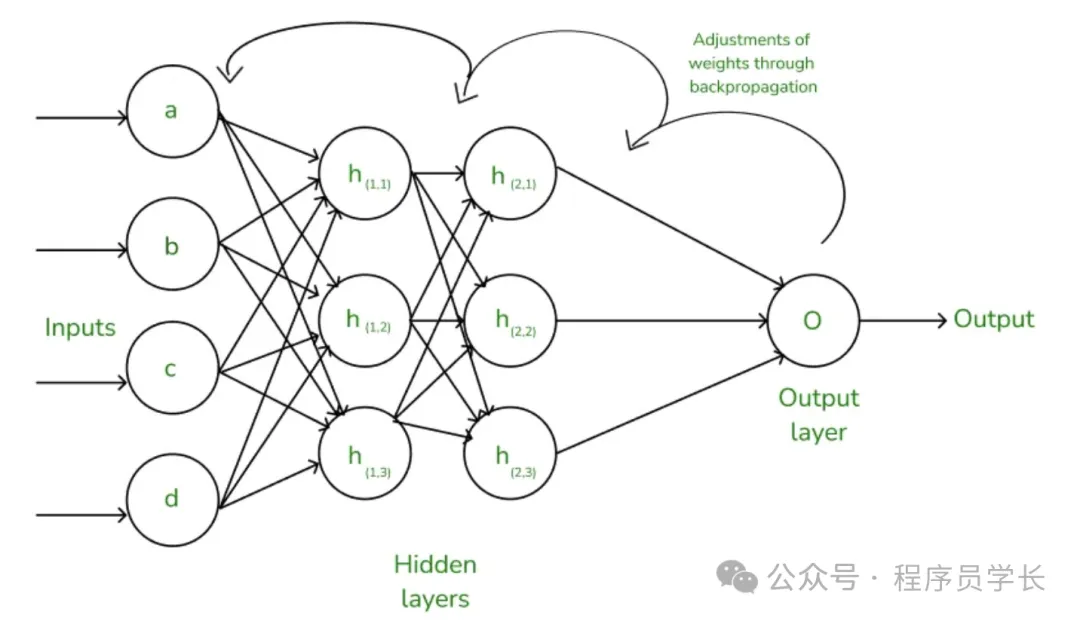
反向传播
反向传播用于计算损失函数对网络中各个参数（权重和偏置）的梯度。
这个过程利用了链式法则，将误差从输出层逐层传播回去，从而更新每一层的参数。
反向传播步骤
- 输出层误差
首先计算输出层的误差，即损失函数对输出层激活值的偏导数其中， 表示输出层的误差， 是激活函数的导数。 - 隐藏层误差
对于隐藏层的神经元，误差由上一层传播过来，通过链式法则计算。
对于第 l 层，误差为：这里， 是第 层的误差， 是第 层的权重转置矩阵， 是激活函数的导数。 - 梯度计算
反向传播中，我们计算每一层的权重和偏置的梯度
- 权重梯度
- 偏置梯度
权重更新
通过反向传播计算得到每一层权重和偏置的梯度后，使用优化算法来更新参数。
其更新公式如下
- 权重更新
- 偏置更新
其中， 是学习率，控制每次更新的步长。
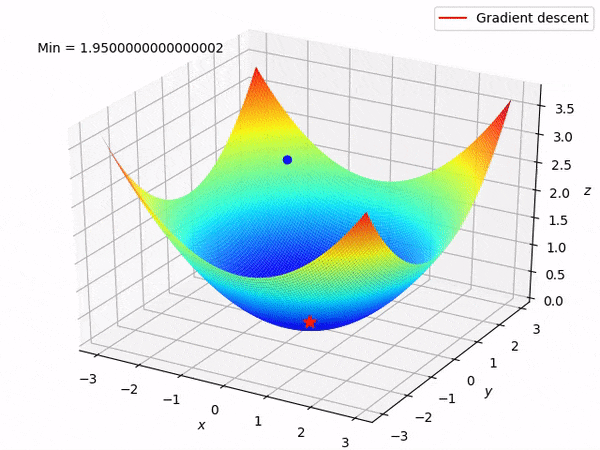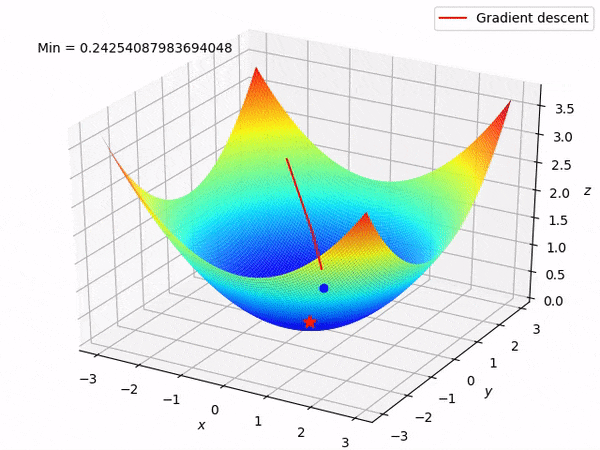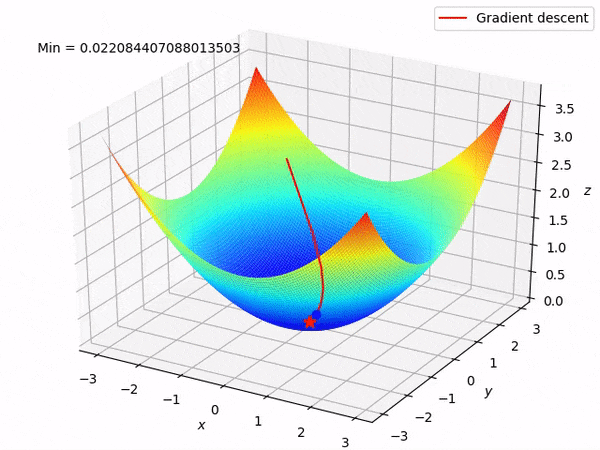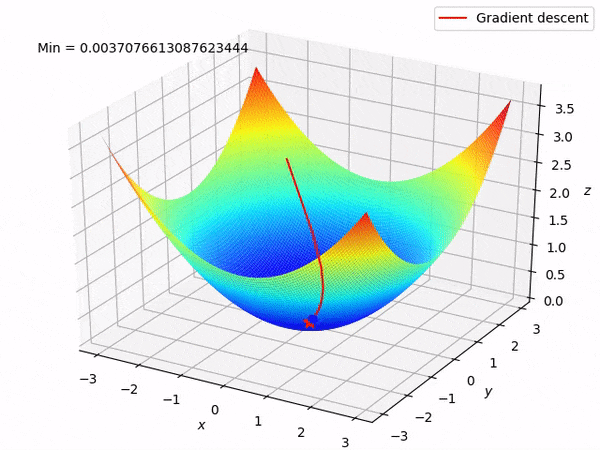
案例分享
下面是一个使用神经网络对鸢尾花数据集进行分类的示例代码。
import numpy as np
import tensorflow as tf
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
# 加载鸢尾花数据集
data = load_iris()
X = data.data
y = data.target.reshape(-1, 1)
encoder = OneHotEncoder()
y_onehot = encoder.fit_transform(y).toarray()
X_train, X_test, y_train, y_test = train_test_split(X, y_onehot, test_size=0.2, random_state=42)
# 构建神经网络模型
model = Sequential([
Dense(10, input_shape=(4,), activatinotallow='relu'), # 输入层，4个输入特征，10个神经元
Dense(10, activatinotallow='relu'), # 隐藏层，10个神经元
Dense(3, activatinotallow='softmax') # 输出层，3个输出类别
])
model.compile(optimizer=Adam(learning_rate=0.01), loss='categorical_crossentropy', metrics=['accuracy'])
# 训练模型
model.fit(X_train, y_train, epochs=100, batch_size=10, verbose=1)
# 评估模型
loss, accuracy = model.evaluate(X_test, y_test, verbose=0)
print(f'Test Loss: {loss:.3f}, Test Accuracy: {accuracy:.3f}')
