你好,我是看山。
布隆过滤器的基本思想
布隆过滤器(Bloom Filter)是1970年由伯顿·霍华德·布隆(Burton Howard Bloom)提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。
布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率和删除困难。
如果想判断一个元素是不是在一个集合里,一般想到的是将集合中所有元素保存起来,然后通过比较确定。链表、树、散列表(又叫哈希表,Hash Table)等等数据结构都是这种思路。但是随着集合中元素的增加,我们需要的存储空间越来越大。同时检索速度也越来越慢,上述三种结构的检索时间复杂度分别为O(n)、O(logn)、O(1)。
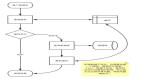
布隆过滤器的原理是,当一个元素被加入集合时,通过K个散列函数将这个元素映射成一个位数组中的K个点,把它们置为1。
 图片
图片
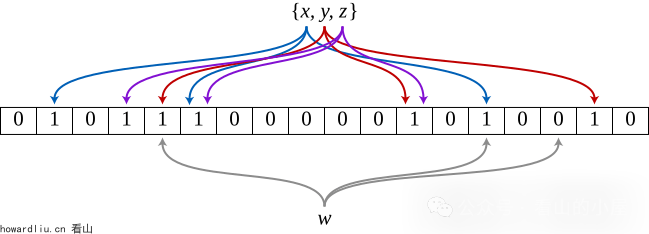
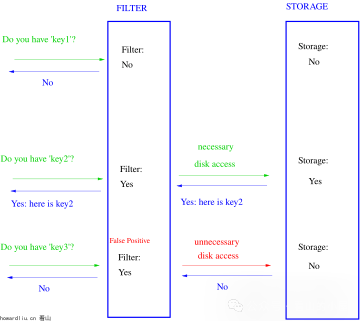
检索时,我们只要看看这些点是不是都是1就(大约)知道集合中有没有它了:如果这些点有任何一个0,则被检元素一定不在;如果都是1,则被检元素很可能在。
 图片
图片
布隆过滤器家族
基于上面的基本思想,结合布隆过滤器算法的优缺点,又衍生出了很多有特殊能力的布隆过滤器,也就是布隆过滤器家族(Bloom Filter Family)。
布隆过滤器(Bloom Filter)
实现逻辑
一种空间效率很高的数据结构,用于判断一个元素是否在一个集合中。实现原理如前文所述。
运行过程
- 插入元素:元素经过多个哈希函数(这里假设为3个,即Hash1、Hash2、Hash3)映射到位数组中的不同位置。例如,元素X经过Hash1映射到位置3,经过Hash2映射到位置7,经过Hash3映射到位置12,然后将这些位置的值设为1。
- 查询元素:当查询元素X时,检查位置3、7、12是否都为1。如果都为1,则认为元素X可能在集合中(存在误报可能);如果有任何一个位置为0,则确定元素X不在集合中。
解决的问题
高效判断元素是否在集合中,在牺牲一定准确性(存在误报)的情况下,大大节省内存空间,提高查询效率,适用于对内存要求苛刻且对少量误报可容忍的场景。
应用场景
在网络、数据库等领域有广泛应用,比如:
- 判断一个数据项是否已经在缓存中,避免不必要的数据库查询,提高系统的响应速度。
- 作为数据库索引的辅助结构,快速确定某个键值是否可能存在于数据库中,辅助索引的精确查找过程;
- 在网络路由中,判断一个IP地址是否属于某个特定的路由区域,快速筛选出可能匹配的路由条目,减少精确查找的范围;
- 用于识别网络流量中的某些特征模式,例如判断一个数据包是否属于某类特定的应用流量(如视频流、音频流等),以便进行针对性的处理(如流量整形、优先级设置等)。
在网络、数据库等领域有广泛应用,例如在缓存系统中判断一个数据项是否已经在缓存中,在网络路由中判断一个IP地址是否属于某个特定的路由区域等。
设计权衡
涉及内存、计算和误报性能之间的权衡。通过调整哈希函数的数量和位数组的大小,可以在不同程度上平衡这些因素。
计数布隆过滤器(Counting Bloom Filter,CBF)
改进点
将布隆过滤器中的1位单元扩展为c位计数器。
运行过程
- 插入元素:元素经过哈希函数映射到位数组中的位置,对应位置的计数器增加。例如,元素X第一次插入时,对应位置的计数器从0变为1。如果再次插入相同元素,计数器继续增加。
- 删除元素:当删除元素X时,对应位置的计数器减1。当计数器为0时,表示该元素已被删除。例如,计数器为2时,删除一次变为1,再删除一次变为0,表示元素已从“可能存在集合中”变为“确定不在集合中”。
解决的问题
解决布隆过滤器无法直接支持元素删除的问题,但引入了较高的内存消耗问题,需要在内存使用和删除功能之间进行权衡。
缺点
c倍地减少了实际可用的位空间(通常为3或4位以避免计数器溢出),导致内存消耗过高,例如在片上内存等资源受限的环境中不太适用。
应用场景
- 在数据库事务中,用于记录某个数据项被操作(如插入、更新、删除)的次数。例如,在一个支持多版本并发控制(MVCC)的数据库系统中,CBF可以用来跟踪每个数据项的不同版本的使用情况,以便在事务提交或回滚时进行正确的处理。
- 用于统计网络中某个源IP地址或某个应用协议的流量出现的次数,帮助网络管理员了解网络流量的分布和使用情况,以便进行网络资源的合理配置和优化。
d-left计数布隆过滤器(d-left CBF,dlCBF)
改进点
基于d-left哈希和元素指纹,通过特定的哈希算法将元素映射到相应位置,利用元素指纹信息进行优化,减少位空间需求。对于给定的目标误报率(fpr),它所需的位空间约为4位CBF的一半。
运行过程
- 插入元素:元素经过d - left哈希和基于元素指纹的处理后,映射到相应位置,计数器增加(原理同CBF,但映射方式更优化)。
- 查询元素:根据优化后的映射关系查询元素对应的计数器值,判断元素是否可能在集合中以及相关操作(如删除时的计数器减1判断)。
解决的问题
在一定程度上解决了CBF内存消耗大的问题,提高了空间效率,同时保持对元素删除的支持,使其更适用于对空间有一定要求的应用场景。
局限性
当目标误报率要与标准布隆过滤器(SBF)相当时,构造所需的空间仍然较大,可能无法满足某些应用的需求。
应用场景
- 分布式系统中的成员资格判断:在分布式系统中,如分布式文件系统或分布式数据库系统,用于判断一个节点是否属于某个特定的集群或组。由于其相对节省空间的特点,在大规模分布式系统中可以有效地减少内存占用,同时保持一定的准确性。
- 内容分发网络(CDN):在CDN中,用于判断一个内容是否已经在某个边缘服务器上缓存。当用户请求一个内容时,首先通过dlCBF快速判断该内容是否可能在本地边缘服务器上,如果可能存在,则进一步精确查找,提高内容分发的效率。
带有变长签名的布隆过滤器(Bloom filter with variable - length signatures,VLF)
改进点
通过只重置k位中的一部分来处理元素删除操作,在插入和查询操作的基础上增加了对部分位重置的逻辑。
运行过程
- 插入元素:元素经过哈希函数映射到位数组中的位置,同时记录相关变长签名信息(图中未详细体现)。
- 删除元素:根据变长签名信息,只重置部分相关位(假设为k位中的一部分)。例如,对于元素X,只重置位置3和7中的部分信息(不是完全重置整个k位),然后更新相关状态以反映元素的删除情况。
解决的问题
尝试解决布隆过滤器的删除问题,但带来了假阴性的风险,需要在删除功能和准确性之间进行平衡。
缺点
存在假阴性问题,即可能错误地判断元素不在集合中,不符合一些应用对准确性的要求。
应用场景
- 数据挖掘中的关联规则挖掘:在数据挖掘中,当挖掘关联规则时,用于快速筛选出可能存在关联关系的数据集。由于其能够处理部分位的重置,在一些需要动态调整关联规则的场景中具有一定优势,例如在市场分析中,根据消费者行为的变化动态调整商品关联规则。
- 文本处理中的关键词过滤:在文本处理中,用于快速过滤出可能包含某些关键词的文档。例如,在搜索引擎中,对大量文档进行预处理时,使用VLF快速筛选出可能与用户搜索关键词相关的文档,然后再进行更精确的文本匹配和排名。
可删除布隆过滤器(Deletable Bloom Filter,DlBF)
改进点
继承了布隆过滤器的简洁性,通过记录插入元素时位碰撞的位置,对可删除位的区域进行紧凑编码(使用部分过滤器内存)。只有一个元素设置的位可以安全删除,若一个元素至少有一个位被重置,则该元素可被有效删除。
运行过程
- 插入元素:元素经过哈希函数映射到位数组中的位置,同时记录位碰撞区域信息。如果发生碰撞,标记相应区域不可删除。例如,元素X插入时,在位置3和7发生碰撞,标记这两个位置所在区域不可删除,其他未碰撞位置所在区域可删除。
- 查询元素:检查元素对应的位置是否都为1来判断是否可能在集合中。
- 删除元素:只清除位于可删除区域的位。例如,对于元素X,如果位置12未发生碰撞且在可删除区域,删除时只重置位置12的值,避免误报的同时实现元素删除。
解决的问题
实现无假阴性的元素删除操作,同时通过合理的设计和参数调整,控制误报率和内存消耗,使其适用于对删除操作有需求且对误报率和内存有一定要求的场景。
性能特点
元素可删除概率与划分的区域数量(r)和过滤器密度(m/n)等因素有关。随着(r)增大,可删除元素的比例增加;随着插入元素增多,删除能力降低。
误报概率的增加是可控的,且与标准布隆过滤器相当。通过实验评估,可删除率与理论预测相符但值相对较低,误报率在元素删除前有可接受的增加,删除元素位后可能会改善。
应用场景示例
在LIPSIN中可用于删除已处理的单向链路标识符,避免环路和删除特殊链路标识;在数据中心环境中可紧凑表示数据包需要经过的一系列中间盒服务,根据匹配情况透明转发数据包并删除服务标识。
- 网络路由中的链路状态维护:在网络路由协议中,如在LIPSIN中,用于删除已处理的单向链路标识符,避免环路的形成,同时可以删除特殊的链路标识(如多跳虚拟链路或控制消息),保持路由信息的准确性和有效性。
- 数据中心的服务链处理:在数据中心环境中,用于紧凑表示数据包需要经过的一系列中间盒服务(如防火墙、负载 balancer、DPI)。当数据包经过中间盒时,根据DlBF的匹配情况透明转发数据包,并在离开中间盒时删除服务标识,提高数据中心网络的处理效率。
压缩布隆过滤器(Compressed Bloom Filter)
改进点
通过使用压缩算法对布隆过滤器的位阵列进行压缩存储,以减少内存占用。
在查询时,需要先解压缩位阵列再进行判断操作。
运行过程
- 插入元素:元素经过哈希函数映射到位数组中的位置,然后对整个位阵列进行压缩存储。
- 查询元素:先解压缩位阵列,再按照布隆过滤器的常规查询方式检查元素是否可能在集合中。
解决的问题
解决布隆过滤器在内存受限环境下的应用问题,通过压缩减少内存占用,但增加了查询时的计算开销,需要在内存和计算效率之间进行权衡。
应用场景
适用于对内存空间要求极为苛刻的环境,例如在一些嵌入式设备或内存受限的传感器网络中,同时对误报率有一定容忍度的场景。
- 嵌入式设备中的数据处理:在嵌入式设备(如智能家居设备、传感器节点等)中,由于内存资源有限,使用压缩布隆过滤器可以在有限的内存空间内实现对数据的快速判断。例如,在智能家居系统中,判断某个设备状态是否已经被记录,以便决定是否需要进一步处理。
- 传感器网络中的事件检测:在传感器网络中,用于快速检测某些特定事件的发生。例如,在环境监测传感器网络中,判断是否出现了某种特定的环境变化(如温度超过阈值、湿度异常等),通过压缩布隆过滤器快速筛选出可能发生事件的传感器节点,然后进行更精确的检测。
分层布隆过滤器(Hierarchical Bloom Filter)
改进点
构建多层的布隆过滤器结构。
通常,上层的布隆过滤器具有较低的精度(较高的误报率)但占用较少的内存,用于快速筛选出可能存在于集合中的元素;下层的布隆过滤器则具有较高的精度(较低的误报率),用于对上层筛选出的元素进行进一步的精确判断。
运行过程
- 插入元素:元素首先进入上层布隆过滤器,上层过滤器具有较低精度(较高误报率),快速筛选出可能存在于集合中的元素。例如,元素X在上层过滤器中被判断为可能存在。
- 查询元素:如果上层判断为可能存在,元素进入下层布隆过滤器进行更精确的判断。下层过滤器具有较高精度(较低误报率),最终确定元素是否在集合中。
解决的问题
提高在大规模数据集上的查找效率,通过分层的方式快速排除大量不可能的元素,减少精确查找的工作量,适用于对查找速度有较高要求的大规模数据应用场景。
应用场景
在大规模数据集的快速查找场景中较为适用。比如:
- 大规模数据库查询优化:在大型数据库的索引结构中,先使用上层的分层布隆过滤器快速排除大量不可能存在的数据项,然后使用下层的过滤器进行更精确的查找,从而提高整体查询效率,减少查询时间。
- 网络搜索中的网页筛选:在网络搜索中,用于筛选海量网页中的相关网页。上层的分层布隆过滤器根据用户搜索关键词快速筛选出可能相关的网页类别,下层的过滤器对这些类别中的网页进行更精确的筛选和排名,提高搜索结果的质量和相关性。
动态布隆过滤器(Dynamic Bloom Filter)
改进点
能够根据数据集的动态变化(如元素的插入和删除频率)自动调整自身的参数,如哈希函数的数量、位阵列的大小等。通常会设置一些阈值和自适应算法来实现这种动态调整。
运行过程
- 插入元素:元素进入动态布隆过滤器,过滤器根据当前的插入和删除频率等动态信息调整自身参数(如哈希函数数量、位阵列大小等),然后按照调整后的规则将元素插入(例如通过新的哈希函数映射到新的位置)。
- 查询元素:按照调整后的参数和规则查询元素是否可能在集合中。
解决的问题
适应数据的动态变化,保持布隆过滤器在不同数据流量和操作频率下的性能,解决固定参数布隆过滤器在动态环境下性能下降的问题。
应用场景
在数据流量不稳定的网络环境中,比如:
- 云计算环境中的资源管理:在云计算环境中,用于动态判断资源是否已被分配(元素是否在集合中)。例如,判断某个虚拟机是否已经被分配了特定的存储资源或网络资源,根据数据流量和资源使用情况动态调整自身参数,提高资源利用效率。
- 移动互联网中的用户行为分析:在移动互联网中,用于分析用户行为模式。根据用户的操作行为(如打开应用、点击链接等)动态调整布隆过滤器的参数,快速判断用户是否执行过某些特定行为,以便为用户提供更个性化的服务和推荐。
布谷鸟布隆过滤器(Cuckoo Bloom Filter)
原理
结合了布隆过滤器和布谷鸟哈希(Cuckoo Hashing)的思想。
它使用多个哈希函数将元素映射到多个桶中,并且在发生冲突时采用类似布谷鸟哈希的方式来处理,即尝试将元素“踢出”已占用的桶并重新放置到其他桶中,同时通过一定的机制来记录这些操作,以支持元素的删除和准确判断元素是否在集合中。
运行过程
- 插入元素:元素经过多个哈希函数映射到多个桶中(假设为两个桶,桶1和桶2)。例如,元素X经过Hash1映射到桶1,经过Hash2映射到桶2。如果桶1已经被占用,按照布谷鸟哈希的方式,将桶1中的元素“踢出”,重新放置到其他桶(可能需要多次尝试和记录相关操作),直到元素X成功插入。
- 查询元素:根据元素映射到的桶以及相关记录的操作信息判断元素是否在集合中。
- 删除元素:根据记录的操作信息,准确删除元素X,例如,如果元素X是通过替换桶1中的元素Y插入的,当删除X时,需要将Y还原到桶1中(或者根据具体的删除逻辑进行正确处理)。
解决的问题
高效处理冲突并支持元素删除,在保证准确性的同时提高数据插入、删除和查询的效率,适用于对操作效率有较高要求且需要处理冲突和支持删除的场景。
应用场景
在需要高效处理冲突且支持元素删除的场景中较为适用,例如:
- 实时数据处理系统中的数据管理:在实时数据处理系统中,用于高效处理数据的插入、删除和查询操作。例如,在一个工业自动化控制系统中,对实时采集的数据进行管理,判断某个数据值是否已经存在于系统中,同时支持数据的插入和删除操作,保证系统的高效运行。
- 内存数据库中的数据存储:在内存数据库中,用于存储和管理数据。由于其结合了布谷鸟哈希的冲突处理机制,在内存有限的情况下,可以高效地利用内存空间,同时保证数据的准确性和可操作性。
文末总结
布隆过滤器为什么这么重要,那是因为有下面四个特点:
- 空间效率:布隆过滤器可以使用相对较少的内存来表示大量元素。
- 快速成员测试:布隆过滤器可以快速确定某个元素是否可能存在于集合中,而无需访问实际的集合数据。
- 可扩展性:布隆过滤器可以处理大量元素,并且无论集合大小如何,都能为成员资格测试提供恒定时间的性能。
- 误报率控制:Bloom Filter 的空间效率的权衡就是误报率的控制。通过调整哈希函数的数量和位数组的大小,可以降低或增加误报率以满足特定要求。
所以,虽然TA有这样那么小毛病,但是我们总有办法适应TA。