本文经自动驾驶之心公众号授权转载,转载请联系出处。
Neural Radiance Fields也就是NeRF,是一种新颖的view synthesis方法,通过优化一个MLP,并使用volumetric ray-marching方法实现了3D场景的隐式表示,但该方法要求costly训练和渲染才能得到较高质量的结果。
3D Gaussian Splatting的出现解决了NeRF的问题,并且同为Radiance Field,3D Gaussian实现了更快的训练和渲染并且能够保证渲染图象的质量(equal or better quality than the previous implicit radiance field approaches)。这个方法在某些数据集上实现了state-of-art质量的结果以及real-time rendering
3D Gaussian
首先需要着重理解3D Gaussian是什么
在光栅化方法中,我们会将点组装为一个个基本图元,其中最常用的图元就是三角形,也就是场景都是由多个三角形面片组成,我们通过光栅化方法将多个三角形画到屏幕上。
但在3DGS算法中,渲染的基本图元变为了3D Gaussian(想象成一个三维空间的椭球体)

多个3D Gaussian会组合重叠
物体表面法线对于场景渲染十分关键,传统的3D重建方法在使用稀疏数据估计物体表面法线上面临挑战,而使用3D Gaussian来表示场景时,可以不需要法线就可以捕获场景的结构。
3D Gaussian的简单公式表示是:
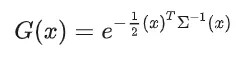
3D高斯函数的形式就是一个椭球体:
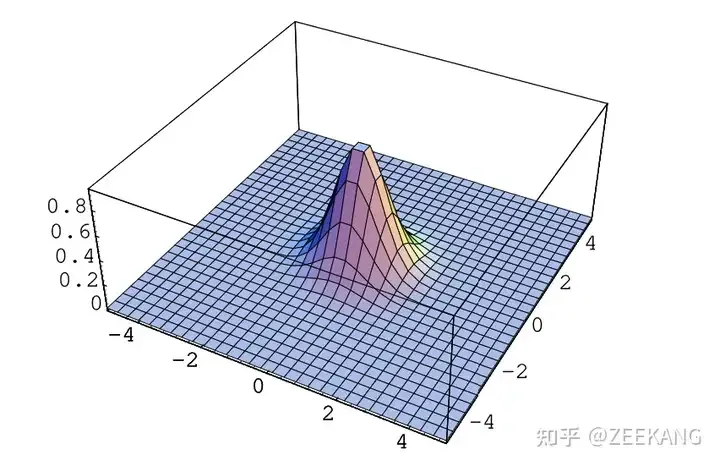
3D 高斯函数的中心点由 均值向量(mean vector)决定(上面的公式中默认均值是0,所以没有显示),椭球体的三个主轴对应着高斯分布的协方差矩阵的特征向量,而主轴的长度则对应着特征值的平方根。这也就是说,协方差矩阵决定了高斯分布在 3D 空间中的形状、大小以及方向。我们再给这个椭球颜色与透明度,来让多个3D Gaussian的组合能够形成高质量图像。然后我们就得到了3DGS算法中定义一个3D Gaussian的参数:
- Position (Mean μ): location (XYZ)
- Covariance Matrix (Σ): rotation and scaling
- Opacity ( ): Transparency,这个参数会在alpha blending阶段时与相乘
- Color (RGB) or Spherical Harmonics (SH) coefficients
3D Gaussian中,协方差矩阵只有在正半定时才有物理意义(或者说协方差矩阵必须是正半定的才行),但传统梯度下降方法很难去对矩阵施加此类约束,可能优化过程中打破了协方差矩阵的正半定性,所以不能用传统梯度下降法。或者说不能将协方差矩阵作为一个优化参数直接优化。
还有一点是,我们能够通过三维空间中的三个点定义任意的三角形一样,我们想要通过某种方式获取任意的椭球形状。
协方差矩阵的几何意义是,表示这个椭圆球在空间中的形状(缩放)和方向(旋转)。协方差矩阵是一个正定矩阵,可以通过某种方式进行矩阵分解。而3D Gaussian中有一种特征值分解,具体形式为:
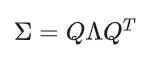
- 协方差矩阵是一个3 X 3 矩阵
- Q是由特征向量组成的正交矩阵(旋转矩阵)。

上面提到过,主轴的长度则对应着特征值的平方根,也就是说可以进一步分解,那么就得到了3DGS原论文中的形式:
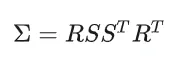

- R是四元数表示的旋转矩阵(此矩阵要保持normalization)
那么不直接对协方差矩阵优化,而是将R,S作为优化参数优化,就可以保持协方差矩阵的正半定。
通过定义R,S以及location(也就是均值),我们可以得到三维空间中所有形式的3D Gaussian。
NeRF的特点就是,它是一个隐式表达的连续的空间,可以使用神经网络进行优化,但无法完全利用GPU进行rendering的加速;传统的使用三角形等Mesh进行的渲染,是显式的离散的空间,可以利用GPU的并行计算来加速渲染,但无法使用神经网络进行优化。而对于3DGS来说,单个3D Gaussian是连续的,可以使用神经网络优化,多个3D Gaussian可以利用GPU进行并行渲染,在两者之间有一个平衡。
Splatting
3D Gaussian是3D物体,要生成图像(就像常规光栅化渲染一样)就需要将其投影到2D平面上。
我们需要实现某种方式,能够将多个3D Gaussian投影到2D image上来渲染结果。
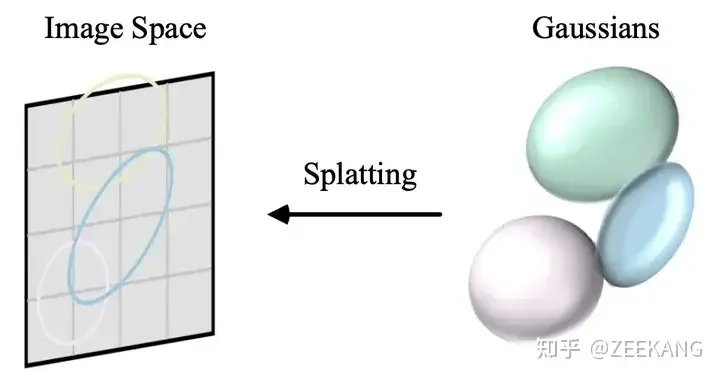
而论文中给出的方式是,替换协方差矩阵为:
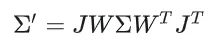
具体来说,仿照渲染管线的流程,假如一个初始的3D Gaussian是在模型空间的话,协方差矩阵就相当于模型变换,将3D Gaussian转换到了世界空间。然后W是View Transform Matrix,将3D Gaussian转换到了相机空间。J是Jocobian Matrix,是用来近似Project Transfor Matrix实现Project Transform。
FAST DIFFERENTIABLE RASTERIZER
假设现在我们已经得到了用于表示整个场景的大量3D Gaussian,现在我们要将其渲染到image上。
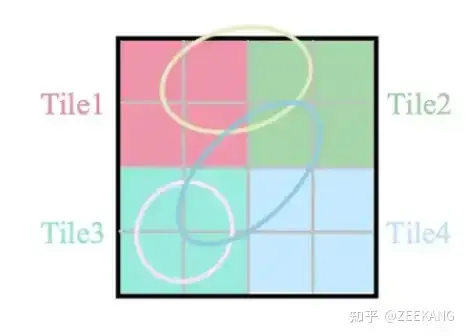
为了加速渲染,3DGS选择使用Tile-based rasterization,将Image切为一个个16 * 16的tile,每个tile像一个小image一样独立计算颜色值,最后多个Tile拼成image的颜色。
考虑到每个3D Gaussian投影到2D image时可能会投影到多个tile,处理方法是如果一个Gaussian投影与多个tile相交,就实例化多次Gaussian,每个Gaussian instance都会得到一个结合view space depth和tile ID得到的key。然后基于这些key,使用single fast GPU Radix sort进行排序。
如下图中,黄色Gaussian投影影响了Tile1和2,其他Guassian投影同理;在另一张图中,我们给出了一个Gaussian投影到多个Tile后,多次实例化以及排序的操作。
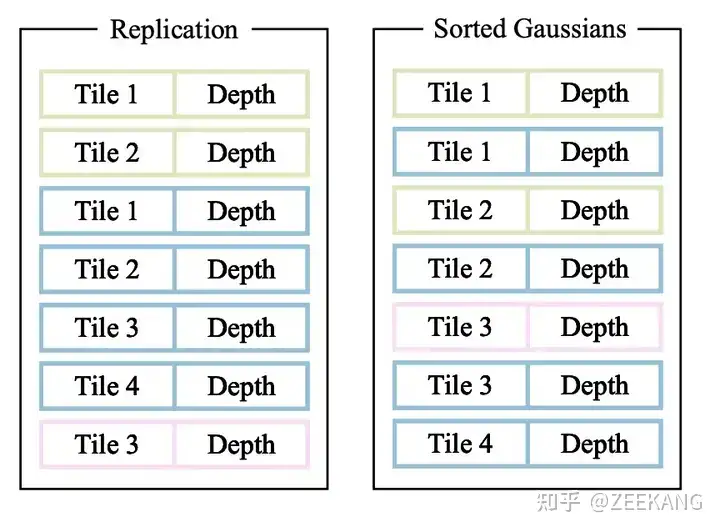
之后,每个Tile分别进行Alpha Blending,计算像素颜色值得到图像。
INITIALIZATION
假如我们已经有方法对3DGS模型进行一步步的优化,那我们要如何开始呢?
在3DGS中,使用的是一种cv算法,Structure from Motion SfM算法来从输入图像中得到一组点云。SfM的基本思路是利用多张包含相同场景不同部分的图像,通过追踪图像中的共同特征,估算出相机的运动路径(即相机的外参,包括位置和平移)以及场景的三维点云结构。而3DGS算法就要利用从SfM算法中得到的初始点云进行初始化。
得到三维点云结构后,算法会将每个点云转换为3D Gaussian,以此为基础训练模型优化。
OPTIMIZATION
Gradient Descent for Parameter OptimizationDesLoss的计算方法很容易想到,就是用同一个视角下,模型生成的图片与实际的训练集图片的对比。
使用随机梯度下降SGD,对Mean、Covariance Matrix、α、Color进行参数优化。
Loss结合了L1和D-SSIM(Structural Dissimilarity Index)。
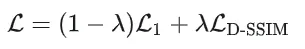
原论文中,=0.2
Adaptive Densification
使用SfM算法初始化了一系列稀疏点之后,adaptive densification方法会动态调整3D Gaussians的数量和密度。

densify简单来说就是,under-reconstructed区域克隆small Gaussians以及在high-variance(我觉得就是Over-reconstructed)区域分离large Gaussian。
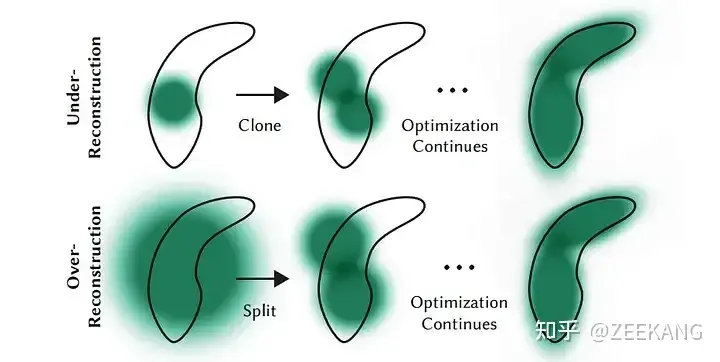
The Process behind 3D Gaussian Splatting
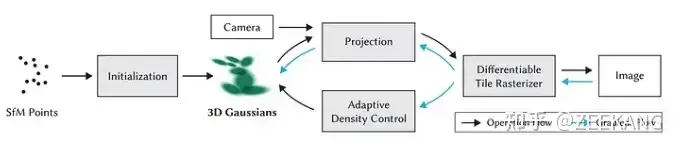
- 使用SfM(Structure from Motion)初步创建一组point cloud
- 将步骤1创建的point cloud转换为3D Gaussian
- 使用SGD训练。训练过程是将3D Gaussian使用differentiable Gaussian rasterization方法rasterize到图像上,通过生成图像与真实图像来计算loss值,调整参数,实现自动densification调整
- Differentiable Gaussian Rasterization
Conclusion
这篇文章对3DGS算法进行了简单的介绍,作为基础简单了解。
下篇文章会深入论文,介绍更多的实现细节。
重要资源
https://github.com/MrNeRF/awesome-3D-gaussian-splatting