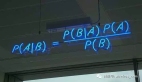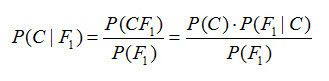贝叶斯概率：从悲剧到喜剧的跌宕历程

在概率论的发展历史上，先后出现过三种定义：经典定义、频率定义和主观定义。

前两种我们在先前文章中有提到，而主观主义指的就是今天这篇文章中要讲的贝叶斯概率。

贝叶斯概率是以发明人的名字命名的。贝叶斯本人是一名牧师，于1761年去世，但贝叶斯定理的正式提出和公开讨论是在1763年，是由贝叶斯的同事代为发表的。

提起贝叶斯概率，在基于统计的机器学习崛起后，它的名字可谓响当当。而且它在概率论三定义中出现又是最晚，有后发优势。

因此，许多同学可能会觉得贝叶斯概率真是含着金钥匙出生、一路顺风顺水的天赐之选啊。

然而，真正了解贝叶斯概率跌宕起伏的经历之后，可能会发出惊叹，算法也如人生啊，人生要经历的磨难算法那里一点也不逊色。

在本篇文章中，我们先简要一下贝叶斯概率的公式，然后列举一个典型的通过贝叶斯概率来解决的邮件分类案例。

接下来，我们再来看一下历史上贝叶斯概率所经历的从悲剧到喜剧的坎坷历程，以及探讨背后的深层次原因。

最后，我们将探讨一下贝叶斯概率在AI中的广泛应用。

1.贝叶斯概率公式

我们先看一下贝叶斯概率的公式：

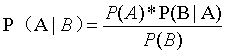
这个公式中包含4项，下面分别说明一下：

先验概率P(A)

主观概率，指的是基于人们主观判断和信念而得出的关于某个随机事件发生可能性大小的估计值。

值得一提的是，贝叶斯概率最开始的悲惨命运，其实主要与P（A）体现出来的主观有关系。

后验概率P(A|B)

后验概率是在观察到某些证据或数据后，对某一事件发生概率的重新评估。

似然函数P(B|A)

似然函数确切来说不是概率，因为是根据已经发生的结果数据来计算。

全（边缘）概率P(B)

全概率公式提供了一种方法，将一个复杂事件的总概率分解为若干个更简单事件的概率的加权和。

似乎每一个都很难懂的样子！先验概率p(A)反而是看着最容易容易的一个。

后验概率P(A|B)和似然函数P(B|A)其实都是条件概率，只是在贝叶斯中所处的位置和作用不同，因此在概念上区分开。

条件概率是指一个事件在另一个事件已经发生的条件下发生的概率。以P(A|B)为例，它表示“在B发生的情况下A发生的概率”。

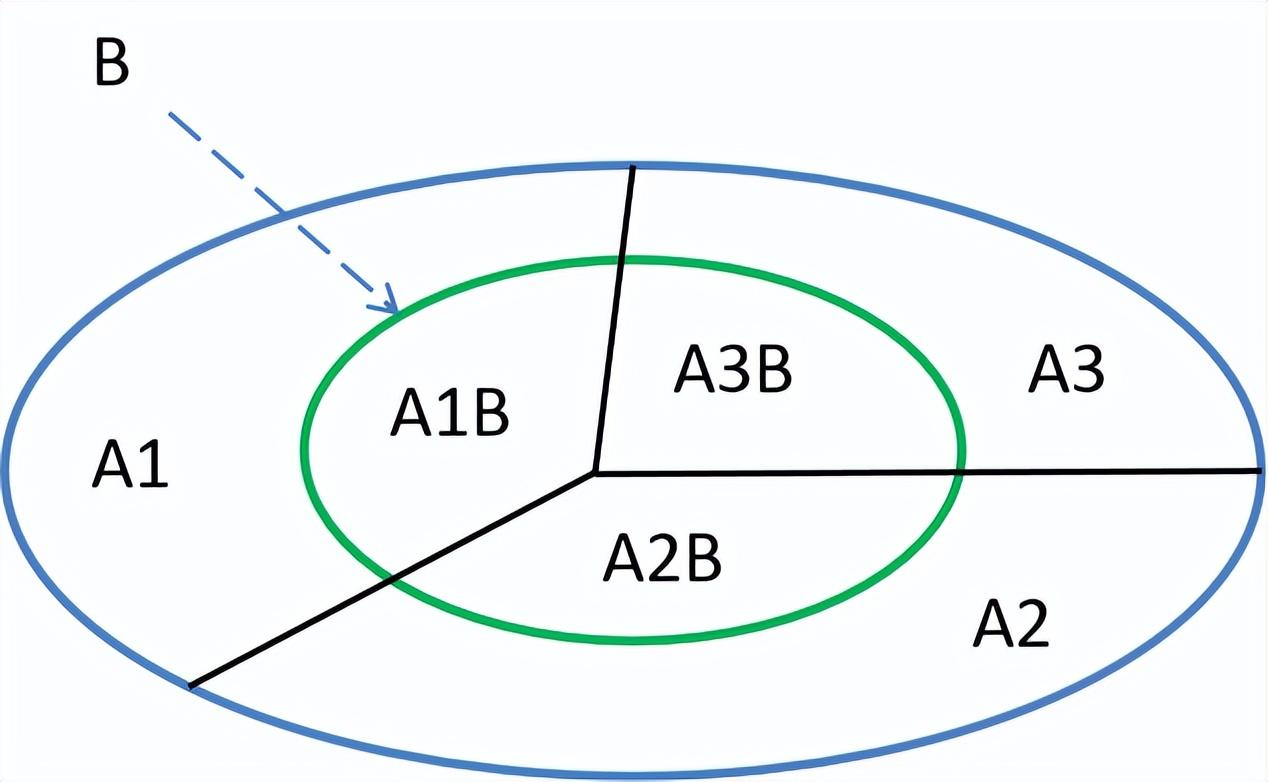
以下面几何图形为例，条件概率计算时，将得到的部分再次设定为整体，并排除掉没有可能性的各个事件之后，重新计算出的比率，如下所示。

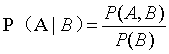
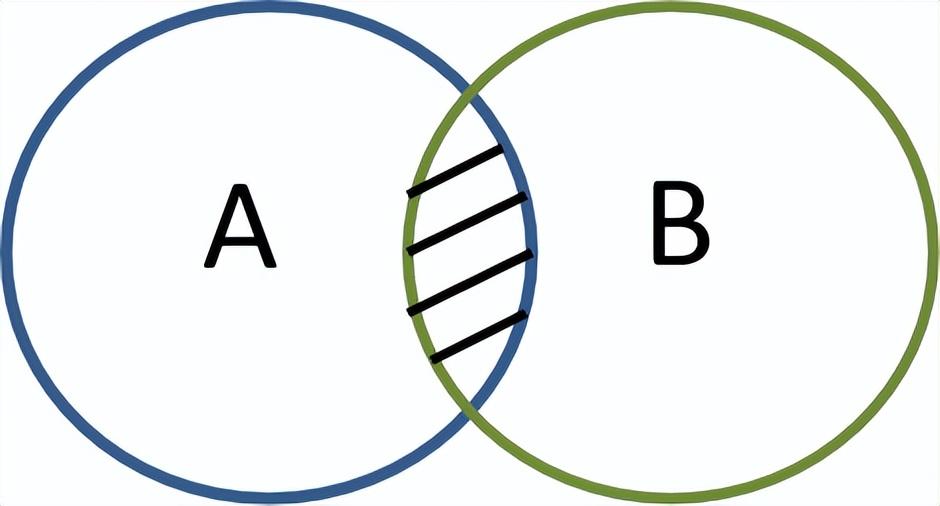
最后，再来看一下全概率或边缘概率，如下几何图形所示。将样本空间B分解为一系列互不相交的事件，并计算这些事件发生的概率之和等于1，计算公式如下。

P(B) = P(A1)*P(B|A1) + P(A2)*P(B|A2) + P(A3)*P(B|A3)

在现实中，全概率往往是最难求解的一项，因为促使样本空间分解的因素往往列不全。

2.垃圾邮件过滤的典型案例

看完上面的数学公式部分之后，相信许多同学记不住。这不能怪你们自己，纯粹的抽象数学公式就是比较反人性的。

有两种方式可以帮忙大家更好地理解贝叶斯概率。一是了解贝叶斯概率的背景和真正目的；另一个是通过具体案例。

先来说第一个。贝叶斯当时为什么要提出这种概率出来呢？他想要解决的问题是什么呢？

实际上，贝叶斯的目的很明确，他想要解决的是逆概率问题。

下面是当时他要求解的问题：“想象一张桌子，上面均匀随机地放着一个白球，而贝叶斯本人背向桌子，对白球位置一无所知。然后，贝叶斯必须从白球位置引出的结果出发，判断这个位置，或者至少给出对应的可能性”。

当然，贝叶斯这个例子不好理解，后面在拉普拉斯那篇文章中，将给出一个更直观的例子。

然而，既然我们知道贝叶斯概率是希望求解逆概率问题。那么，我们可以将上面的数学公式替换一下，这样能帮助大家更好的理解。

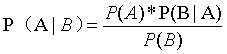
相当于

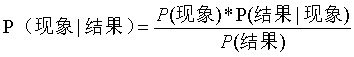
因为，正概率说的是先有现象，然后去推测结果发生的概率。

那么，所谓的逆概率，就是在知道结果的情况下去反推现象（也可以理解成原因）出现的概率。

接下来，我们再通过一个垃圾邮件分类的例子，让大家直观地感受一下贝叶斯概率的应用。

构建邮件数据集

构建一个简化的贝叶斯垃圾邮件过滤数据集。

邮件特征

只考虑两个特征，即邮件中是否包含“免费”、“中奖”这两个词

邮件类别

邮件分为两类，垃圾邮件（Spam）和非垃圾邮件（Not Spam）

先验概率

假设我们从历史数据中得知，垃圾邮件占所有邮件的30%，非垃圾邮件占70%

P(Spam) = 0.3

P(Not Spam) = 0.7

条件概率

假设在垃圾邮件中，包含“免费”的概率是80%，包含“中奖”的概率是70%

P(免费|Spam) = 0.8

P(中奖|Spam) = 0.7

在非垃圾邮件中，包含“免费”的概率是10%，包含“中奖”的概率是5%

P(免费|Not Spam) = 0.1

P(中奖|Not Spam) = 0.05

新邮件特征

假设我们收到一封新邮件，它同时包含“免费”和“中奖”两个词

使用贝叶斯定理计算后验概率

我们需要计算这封邮件是垃圾邮件的概率P(Spam|免费，中奖)和不是垃圾邮件的概率P(Not Spam|免费，中奖)

使用贝叶斯定理，我们可以得到

由于我们假设免费和中奖是独立的，我们可以得到垃圾邮件中的联合概率

P(免费，中奖|Spam) = P(免费|Spam)* P(中奖|Spam) = 0.8*0.7 = 0.56

P(免费，中奖|Not Spam) = P(免费|Not Spam)* P(中奖|Not Spam) = 0.1*0.05 = 0.005

决策

因此，该封邮件是垃圾邮件的概率更大一些。

3.贝叶斯概率从悲剧到喜剧的三段经历

贝叶斯概率从诞生到AI时代的火热，大致经历了以下三个阶段。

第一阶段：从出现到确立

核心事件1：1763年，托马斯贝叶提出贝叶斯定理，求解逆概率问题；

核心事件2：1774年，拉普拉斯发表《论事件原因存在概率》，综合了正、逆概率，贝叶斯正式作为逆概率的标准。

第二阶段：从寒冬到曙光

核心事件1：拉普拉斯方法中的主观置信度（即贝叶斯概率部分）受到强烈批评，如哲学家密尔形容为“心智失常”，“自称是科学，其实是无知”，统计学家费希尔“谬误的垃圾”；

核心事件2：20世纪初，数理统计学科出现，主流统计学将贝叶斯概率排斥之外；

核心事件3：1933年，安德烈.柯尔莫洛夫，提出概率公理，柯尔莫洛本人是频率学派。

第三阶段：从认可到爆发

核心事件1：20世纪50年代，萨维奇发布《统计学基础》，提出贝叶斯公式是唯一的推理工具；

核心事件2：20世纪60年代，雷所罗门诺夫将图灵的可计算性理论与贝叶斯公式结合起来，这就是人工智能一般性框架的前身；

核心事件3：20世纪80年代，蒙特卡洛模拟方法的出现，特别是马尔科夫链蒙特卡洛方法（MAMC），给贝叶斯公式的实际应用带来了革命。

4.贝叶斯概率坎坷历程的原因剖析

从上面贝尔斯概率的经历中，可以发现贝叶斯概率在历史上大部分时间之内，都处于一种边缘、受排斥的位置上。

它只是一种数学方法而已，原因到底为何呢？

一是计算复杂性，古代没有计算机，计算器也没有.而在贝叶斯定理中，计算后验概率通常需要对所有可能的参数值进行积分，这在数学计算上是比较复杂的。

在计算技术不发达的时代，这种计算上的困难限制了贝叶斯方法的广泛应用。但是，显然这个原因顶多会导致不使用，不至于受排斥。

二是主观性问题，贝叶斯定理依赖于先验概率，即在观察数据之前对事件发生概率的估计。

这种先验概率的设定被认为带有主观性，因为不同的人可能会基于不同的信息或信念设定不同的先验概率。

在科学界，尤其是频率学派的统计学家看来，这种主观性是不可接受的，他们更倾向于基于数据本身来估计概率，而不依赖于任何先验信息。

在我们看来，主观或者客观更多的是的一种认识和利用世界的手段而已，显然还有更深层次的原因。

三是秩序性问题，这才是贝叶斯定律在历史上遭遇冷遇的根本原因。在哲学的理性主义时代，人们普遍认为真理是客观存在的，这种秩序观强调世界的运行遵循固定的、可预测的规律，而这些规律是独立于人的主观意识的。

换句话说，社会中的分层、权威等也是客观决定的，不决定于人主观的意识，否则社会只会变得混乱。

接着，我们再来探讨一下，历史上又是那些因素最终拯救了贝叶斯概率呢？

首先，计算机与马尔科夫链蒙特卡洛（MCMC）方法的出现，从根本上解决了贝叶斯方法在算力和积分计算上的瓶颈。

当然，这不是主要原因，因为如果人们的认知不发生改变的话，再好的工具放在手里都起不到应有的作用。

其次，实用主义哲学的兴起，为贝叶斯概率理论提供了坚实的哲学基础，解决了主观与客观之间的长期争论。

实用主义强调“好不好用”，而不刻意追求所谓的“正不正确”。在这一哲学背景下，贝叶斯方法中先验概率的主观性不再是障碍。

这一观念的转变，最终使得贝叶斯概率理论从边缘走向主流，被广泛接受为处理不确定性问题的有效工具。

5.贝叶斯概率在AI中的应用

贝叶斯概率理论作为统计学与人工智能领域的一颗璀璨明珠，其影响力深远，构成了贝叶斯学习、贝叶斯推理、贝叶斯网络、贝叶斯决策以及贝叶斯优化等一系列核心理论的基石。

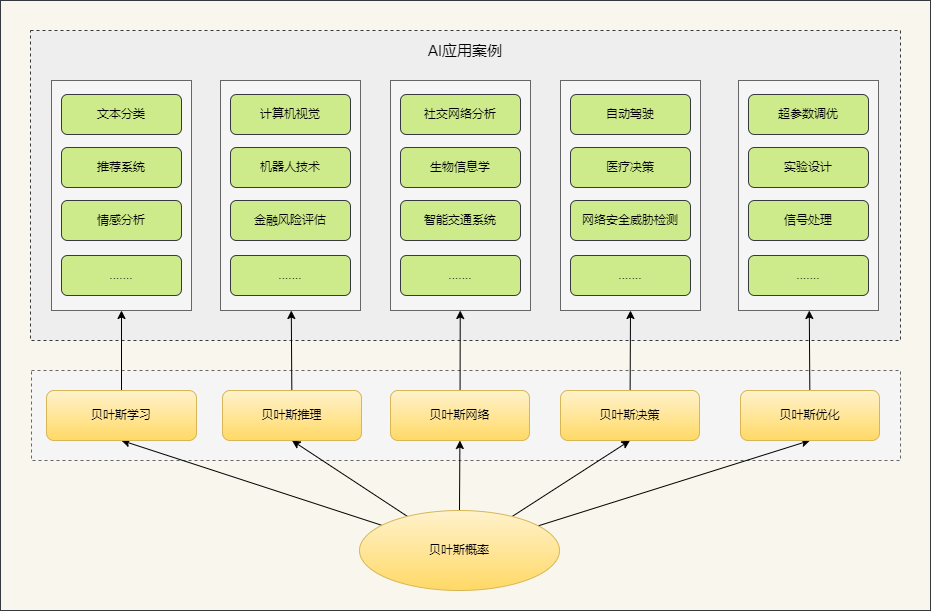
一是贝叶斯学习。它的优势在于其独特的增量学习能力，它允许模型在训练过程中不断更新参数的概率分布。

这种动态调整的能力使得模型能够适应不断变化的数据环境，实现自我优化和提升，特别适合在处理变化数据和在线学习场景中。

二是贝叶斯推理。它作为一种基于贝叶斯定理的统计推理方法，不仅能够提供参数的点估计，更重要的是，它能够提供参数的分布信息，这为理解和量化模型的不确定性提供了有力工具。

在AI领域，贝叶斯推理被广泛应用于不确定性量化、模型选择和模型比较，为决策提供更全面、更可靠的依据。

三是贝叶斯网络。作为一种概率图模型，通过有向无环图（DAG）巧妙地表示变量之间的条件依赖关系，为处理复杂不确定性问题提供了强大的工具。

在知识表示、推理、预测和决策支持系统中，贝叶斯网络的应用无处不在，它能够帮助我们理解和预测复杂系统的动态行为，为决策提供科学依据。

四是贝叶斯决策。它将贝叶斯概率与决策理论完美结合，为在不确定性下做出最优决策提供了系统性的解决方案。

它考虑了决策的后果和不确定性，通过最小化预期损失或最大化预期效用，可以帮助我们在复杂多变的环境中做出更适合的选择。

五是贝叶斯优化。通过构建目标函数的概率模型，贝叶斯优化能够高效地搜索最优解，尤其适用于高维、非凸或计算成本高的优化问题，如超参数调优、神经架构搜索和实验设计等。

6.小结

人生就像是一个大戏台，不同的人在舞台上扮演着不同的角色。同样，算法的世界也是一方广阔的舞台，不同的算法的命运也各不相同。

像贝叶斯算法，尽管生不逢时，但正如金子早晚会发光，贝叶斯算法也在人类文明逐步走向数字化、智能化的路途中，发展成为一个举足轻重的算法。

并且，贝叶斯概率，如今也已经超越了其最初的数学领域，成为了一种理解和解释世界的哲学。