十分钟了解UV统计算法HyperLogLog-51CTO.COM

前段时间产品提了个需求，需要统计APP的各个场景下的UV，如何实现？

1、方案

考虑到上述问题的扩展性，除了统计APP每日的独立用户登录数，还需要统计打开每个页面的独立用户数。

方案一：用Set统计

首先我们想到肯定是通过类似 redis 的 Set，将每个openid添加到对应需要统计的 Set 中，每一种类型用一个 Set，那计算一下，如果存储1亿个key，每个key的大小32个字符，大约存储空间是：

100000000 * 32 * 8 = 23G

以上只是计算一种类型，如果有100种类型，那么这个存储空间线性增长。当然，对于存储多个类型可以通过稀疏矩阵优化，但是实际的存储空间还是比较大。

方案二：用bitmap统计

方案一最大的问题是存储 Set，但是我们需要的信息是存在或者不存在，那么这里其实用 bitmap 位运算0或1就可以解决当前问题，那么存储1亿个key，每个key需要1个bit位，大约存储空间是：

100000000 * 1 / 8 = 12M

如果有100种类型，那么存储空间是1.2G左右，这种方法可以解决内存过大的问题，但是无法扩展。

方案三：概率算法统计

在解决大数据量的情况下，很多实际场景不需要太精确的数据，为了节省内存同时满足大数据的统计需求，衍生了很多概率算法，如：

Linear Counting：定义一个hash函数，function hash(x): -> [0,1,2,…,m-1]，假设该hash函数的hash结果服从均匀分布，接着定义一个长度为m的bit数组，开始每一位上都初始化为0，然后对可重复集合里的每个元素进行hash得到k，如果bitmap[k]为0则置1，最后统计bitmap数组里为0的位数；
LogLog Counting：LogLog Counting优于Linear Counting，也是利用哈希函数将输入元素映射到一个固定大小的位数组中，估算连续数组的位数，时间复杂度为O(1)；
HyperLogLog Counting：是基于LogLog Counting的改进方案，能实现更小的误差，本文重点就介绍HyperLogLog Counting算法；

2、HyperLogLog Counting原理

用一句话概括：我们能找到连续出现的概率与次数的关系，能就能将其转换为数学公式。比如我们有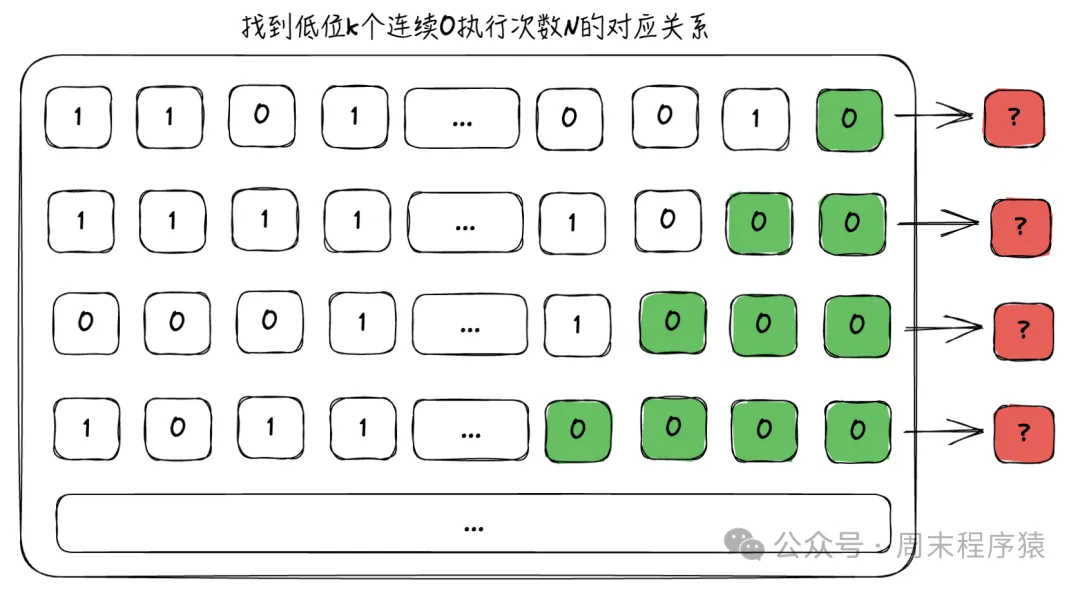数组：

数组

通过上图我们只需要末尾连续0的个数，并统计出执行多少次随机即可，我们用如下代码实验：

import random
import math

class LogLogV1:
    def __init__(self, maxbit: int, tries: int = 10):
        """
            maxbit: int, 连续0的个数
            tries: int, 重复次数
        """
        self.maxbit = maxbit
        self.tries = tries
        self.option = [0, 1]

    def _run_one_round(self):
        rounds = 0
        while True:
            num = 0
            while True:
                result = random.choice(self.option)
                if result == 1:
                    break
                num += 1
                rounds += 1
            if num >= self.maxbit:
                break
        return rounds
    
    def get_rounds(self):
        all_rounds = 0
        for i in range(self.tries):
            all_rounds += self._run_one_round()
        return all_rounds / self.tries

if __name__ == '__main__':
    for i in range(10, 20):
        be = LogLogV1(i)
        rounds = be.get_rounds()
        print(f"{i} rounds: {rounds}, log2: ", math.log(rounds, 2))

以上代码的含义是，获得连续 maxbit = 0，需要执行的次数是多少，这里通过 tries 重复次数来求平均值，最后输出：

10 rounds: 1023.7, log2:  9.99957727351139
11 rounds: 2041.0, log2:  10.995060467032719
12 rounds: 2649.1, log2:  11.371286589215627
13 rounds: 16484.6, log2:  14.008831259883943
14 rounds: 20324.1, log2:  14.31090384726008
15 rounds: 25673.7, log2:  14.648003606393374
16 rounds: 70248.2, log2:  16.10017363855784
17 rounds: 152139.1, log2:  17.2150314501608
18 rounds: 267469.5, log2:  18.029014862371255
19 rounds: 627246.3, log2:  19.258672529927942

可以看到 2^maxbit ≈ rounds，其中误差比较小。

3、HyperLogLog Counting分桶

为什么要分桶？假设上述的tries值比较小，那么会存在估计不准的情况，比如 2^maxbit ~ 2^(maxbit+1) 之间直接按照公式计算，误差会比较大，所以通过求多个值得平均值来解决问题，这样估算的值就比较平滑。

那么redis的HyperLogLog Counting是如何分桶的？代码：https://github.com/redis/redis/blob/unstable/src/hyperloglog.c

2^14个桶，每个桶6bit，总共12KB；
每个输入通过hash算法得出64bit哈希值hashkey；
hashkey的低14位，用来选择桶号（0-2^14-1号）Mi;
hashkey的高50位,用来找K（也就是第一次出现1的位置，或者说0后缀的长度），把K存入Mi；

网上有个模拟演示地址：http://content.research.neustar.biz/blog/hll.html，有兴趣可以看看详细的执行过程。

4、扩展

（1）HyperLogLog能满足产品的需求，但是扩展到其他问题：如何实现长周期存储（一年的存储周期UV统计）；（2）如何实现分布式，本身HyperLogLog是单机算法，如何实现非集中式场景；

参考

https://www.cnblogs.com/wmyskxz/p/12396393.html