布隆过滤器（Bloom Filter）是一种概率型数据结构，用于判断一个元素是否属于一个集合。它特别擅长处理大规模数据的快速查找，具有高效的空间利用率和查询速度。下面是布隆过滤器的工作原理、优缺点和使用场景。
工作原理
(1) 初始化：布隆过滤器初始化时，创建一个长度为m的位数组（bit array），所有位初始化为0，并选择k个独立的哈希函数。
(2) 添加元素：将一个元素添加到布隆过滤器时，使用k个哈希函数对该元素进行哈希运算，得到k个哈希值（位置）。然后，将位数组中这k个位置的值设为1。
(3) 检查元素：要检查一个元素是否在布隆过滤器中，同样使用k个哈希函数对该元素进行哈希运算，得到k个哈希值（位置）。检查位数组中这k个位置的值：
- 如果所有位置的值都是1，则判断该元素可能在集合中。
- 如果有一个位置的值是0，则判断该元素肯定不在集合中。
示例展示
首先，一个空的布隆过滤器是一个 m 位的位数组，所有位都设置为零，如下所示：
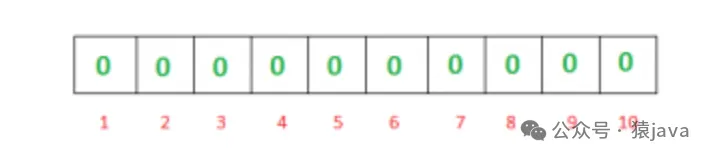
我们需要使用 k个哈希函数来计算给定输入的哈希值。当我们想要将一个项目添加到过滤器中时，会设置索引h1(x)、h2(x)、… hk(x)处的位，其中索引是使用哈希函数计算的。例如，假设我们想要将“java”输入过滤器，我们使用3个哈希函数和一个长度为10的位数组，初始时所有位都设置为0。首先我们将计算哈希值如下：
h1(“java”) % 10 = 1
h2(“java”) % 10 = 4
h3(“java”) % 10 = 7注意：这些输出仅用于解释。然后我们会将索引1、4和7处的位设置为1：
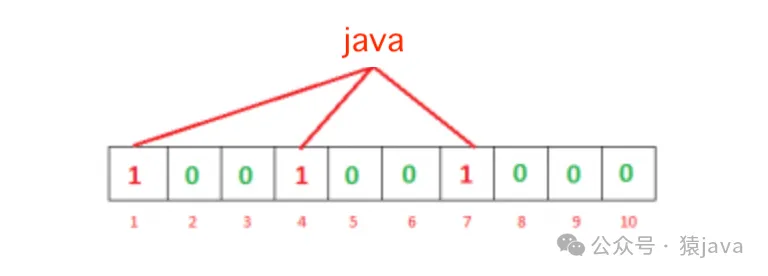
再次，我们想要输入“python”，同样地，我们将计算哈希值：
h1(“python”) % 10 = 3
h2(“python”) % 10 = 5
h3(“python”) % 10 = 4将索引3、5和4处的位设置为1，如下图：
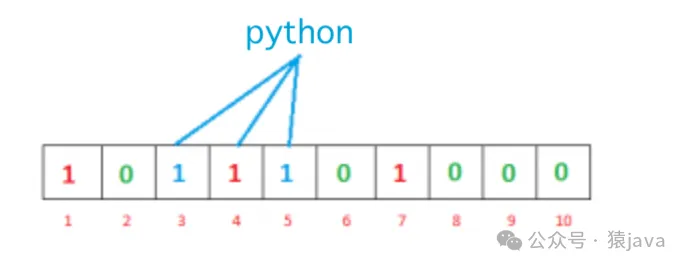
现在，如果我们想要检查“java”是否存在于过滤器中。我们将执行相同的过程，但这次是反向的。我们使用h1、h2和h3计算相应的哈希值并检查这些索引处的所有位是否都设置为1。如果所有位都设置为1，我们可以说“java”可能存在。如果这些索引处的任一位为0，则“java”肯定不存在。
为什么说：如果所有位都设置为1，我们可以说“java”可能存在？为什么有这种不确定性。让我们通过一个例子来理解这一点。假设我们想要检查“rust”是否存在，将使用h1、h2和h3计算哈希值：
h1(“rust”) % 10 = 1
h2(“rust”) % 10 = 3
h3(“rust”) % 10 = 7如果我们检查位数组，这些索引处的位都设置为1，但我们知道“rust”从未被添加到过滤器中。索引1和7处的位是在我们添加“java”时设置的，索引3处的位是在我们添加“rust”时设置的。
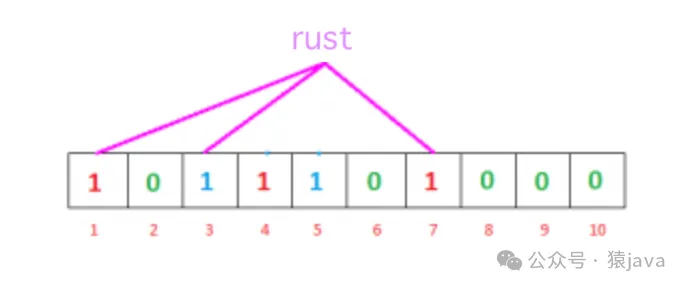
因此，由于计算出的索引处的位已经被其他项目设置，布隆过滤器错误地声称“rust”存在，并生成了一个假阳性结果。根据应用程序的不同，这可能是一个巨大的缺点或者是相对可以接受的。
优缺点
优点：
- 空间效率高：相比其他数据结构如哈希表，布隆过滤器的空间利用率非常高。
- 查询速度快：查询操作只需要进行k次哈希运算和k次数组访问，速度非常快。
- 插入操作高效：插入操作同样只需要进行k次哈希运算和k次数组访问，效率高。
缺点：
- 误判率：布隆过滤器可能会误判，即可能会错误地认为某个元素在集合中（假阳性），但不会出现假阴性（即不存在的元素被误判为存在）。
- 无法删除元素：标准的布隆过滤器不支持删除操作，因为删除操作可能会影响其他元素的查询结果。不过，可以使用计数布隆过滤器（Counting Bloom Filter）来支持删除操作。
- 哈希函数选择：需要选择合适的哈希函数，以保证哈希值均匀分布，避免过多的冲突。
使用场景
- 网页去重：在搜索引擎中，布隆过滤器可以用于判断网页是否已经被抓取过，从而避免重复抓取。
- 缓存系统：在分布式缓存系统中，布隆过滤器可以用于快速判断某个数据是否在缓存中，从而减少对后端数据库的查询压力。
- 垃圾邮件过滤：在邮件系统中，布隆过滤器可以用于快速判断邮件是否为垃圾邮件，提高过滤效率。
- 数据库查询优化：在数据库系统中，布隆过滤器可以用于快速判断某个记录是否存在，从而减少磁盘I/O操作，提高查询效率。
总结
布隆过滤器是一种简单但非常有效的数据结构，特别适用于大规模数据的快速查找和去重等场景。尽管它有一定的误判率，但在很多应用中，这一点点误判是可以接受的。
