本文作者来自香港城市大学和华为诺亚方舟实验室。其中,第一作者姚宇璇是香港城市大学计算机系的二年级博士生,研究方向涉及大模型的复杂推理和生成,师从宋林琦教授。吴涵,郭志江是华为诺亚方舟实验室研究员。
大型语言模型(LLMs)虽然进展很快,很强大,但是它们仍然存在会产生幻觉、生成有害内容和不遵守人类指令等问题。一种流行的解决方案就是基于【自我纠正】,大概就是看自己输出的结果,自己反思一下有没有错,如果有错就自己改正。目前自己纠正还是比较关注于让大模型从错误中进行学习。更多相关内容可以参考这篇 TACL 的 survey [1]。
但是呢,现有的很多自我纠正的方法依赖于复杂的 prompt engineering,人类反馈,或外部工具,但这些方法往往比较麻烦(试 prompt),不稳定(换了个模型 prompt 可能就要修改了),昂贵(人类反馈很贵的),增加时延(要调用不同的外部工具)。为了克服这些限制,本文提出了一种无需 prompt engineering 也无需外部反馈的方法 ——Learning from Correctness(LeCo,是的,作者们是乐高爱好者 XD),我们想倒反天罡,从正确而不是错误中进行学习,让自己变得更强大。

- 论文链接:https://arxiv.org/pdf/2403.19094arxiv.org/pdf/2403.19094
- 代码链接:https://github.com/starrYYxuan/LeCo
一句话总结:LeCo 通过大模型自己生成的推理步骤进行自我纠正,无需人类反馈,手工提示和外部工具。其核心思想就是:模型如果知道更多的正确推理步骤,那他的搜索空间就可以压缩,从而更有高效地找到完整的正确推理路径。LeCo 为每个推理步骤计算置信度分数,通过分数给推理步骤打分,低分的推理步被视为潜在错误,之前的步骤被视为正确。通过将这些正确步骤附加到输入中,模型可以逐步接近正确答案。如下图所示,LeCo 首先得到对当前问题的解(左边 output), 然后我们逐渐去收集正确的推理步骤知道得到最后正确的解。这种渐进式学习方法不仅提高了推理准确性,还减少了 tokens 消耗(穷人友好)和迭代次数(和投票,从错误中学习相比)。
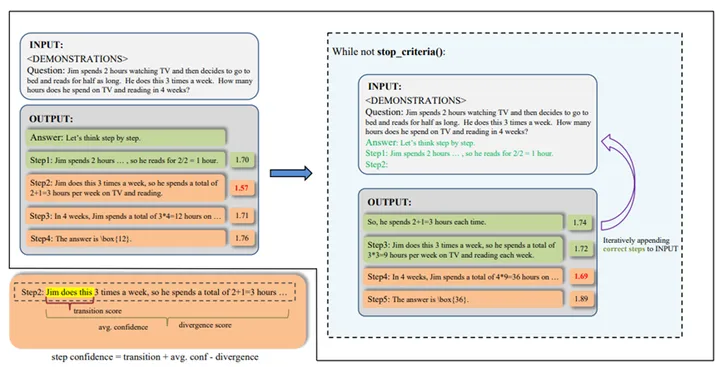
LeCo 方法示意图
如何找出正确的推理步骤?
一些预设知识:在生成任务中,logits 代表候选词被选为下一个词的对数概率。另一方面,置信度指的是模型对其预测的确定性。在推理任务中,我们提出步骤置信度来衡量模型对每个推理步骤的正确性的置信度。于是我们设计了三种基于 logits 的评分,从单步推理步和不同推理步出发,全面评估每个推理步骤的置信度。
方法:为了找出大模型自己生成的正确推理步骤,本文开发了一种基于生成 logits 的高效方法来测量每个推理步骤的置信度,无需额外标注或工具。通过综合考虑每个步骤中的平均置信度、步骤置信度差异和步骤传递概率,LeCo 能识别出近 65% 的错误步骤。具体来讲,我们的置信度设计考虑了 3 个不同的角度:
单步置信度(average token score):一种简单的方法来衡量步骤置信度是平均计算某一步中的 token 概率。这个平均值反映了模型在该步骤中推理的确定性。单步置信度定义为:
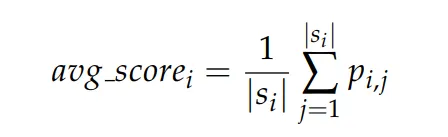
单步散度分数 (step divergence score):虽然平均 token 概率看似直观,但它可能会产生误导。在一个步骤中,大多数 token 通常是常见词汇,具有高置信度分数,但携带的信息很少。相反,对于推理至关重要的 token,例如数学计算,通常置信度较低。这种矛盾导致整个步骤的平均 token 置信度偏高。为了解决这个问题,本文提出了 Step Divergence Score。这个指标测量了步骤中标记概率的分布均匀性。理想情况下,正确的推理步骤 token 概率不仅高,而且在所有 token 之间均匀分布。为此我们定义了 token 概率的归一化分布
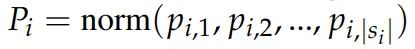
和均匀分布 U 来设计:
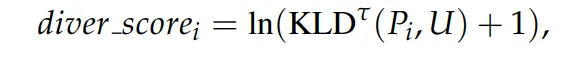
步间转移分数 (Inter-step Transition Score) : 在步骤内部测量之后,我们寻求量化连续步骤之间的转换。初步实验发现了两个关键点:
(1)整体置信度较低的步骤倾向于在初始的几个 tokens(通常是前三个)中具有较低的置信度,更多讨论可以在附录中找到。
(2)这些初始的几个 tokens 也是在不同程序运行中最有可能改变的。基于这些观察,我们建议使用步骤中的开头的借个 tokens 概率来表示该步骤和下一个步骤之间的交叉转换分数。换言之,转换分数:
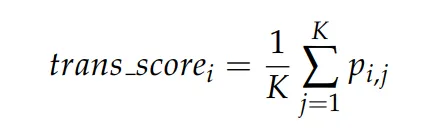
结合以上三个分数,我们可以得到针对每个推理步骤的置信分数:
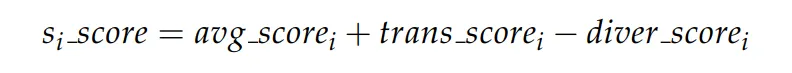
LeCO:从正确的推理步中学习
好了,现在我们已经拥有了衡量推理步置信分数的方法,现在只需要迭代式地收集正确的推理步骤,优化搜索空间去拿到最后的正确推理路径。LeCo 分为两个阶段:
- 初始阶段(Initial Stage):用任何 CoT 的方法生成一个初始的解即可,要求就是需要这个解是有推理步骤的。
- 反思阶段(Rethink Stage):拿到这个解之后,我们用上述方法去计算每个推理步骤。然后选择分数最低的那个步骤作为 “犯错的第一步”。之前的的推理步骤我们都认为是 “正确的步骤”。然后我们将正确的步骤也作为输入给到大模型去进行推理。
LeCo 就是在推理和反思两个阶段交替进行直到达到停止的条件。我们设置的条件有两个:1. 达到最大的迭代次数;2. 连续两次的解都是一致的。
LeCo 算法总结如下:

实验结果
我们使用 LeCo 在推理任务上面进行了验证,包括逻辑推理,常识推理和数学推理。对比的基线系统包括了也是需要多次推理的 Self-Consistency(SC [2]),Adaptive Consistency(ADPSC [3])和 Recursively Criticizes and Improves(RCI [4],从错误中学习):
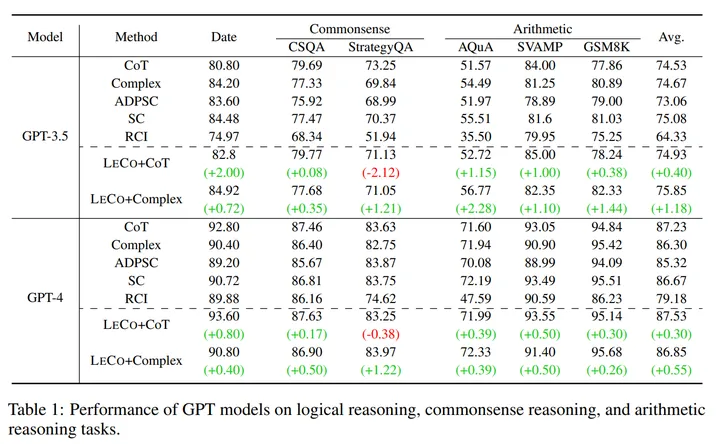
表 1:LeCo 在逻辑,常识和数学推理上面的性能表现
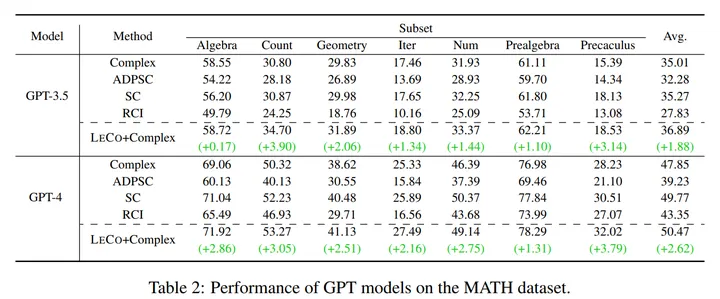
表 2:LeCo 在需要更加复杂的推理 MATH 上的表现
从上面的两个表格中我们可以看到:
- LeCo 的普适性:适用于不同的模型(GPT3.5,GPT4,DeepSeek)和不同的 CoT 方法(Initial Stage 用的);
- LeCo 的性能提升:在不同类型的推理任务上面都有提升,越难的任务,需要越多推理步骤的任务提升越多(比如 MATH);
- LeCo 的效率提升:如下两个表格所示,LeCo 除了在各种任务上对性能有一定提升之外,所消耗的 token 数量更少(如:比 self-consistency 低 80%),并且所需的迭代轮数更低。
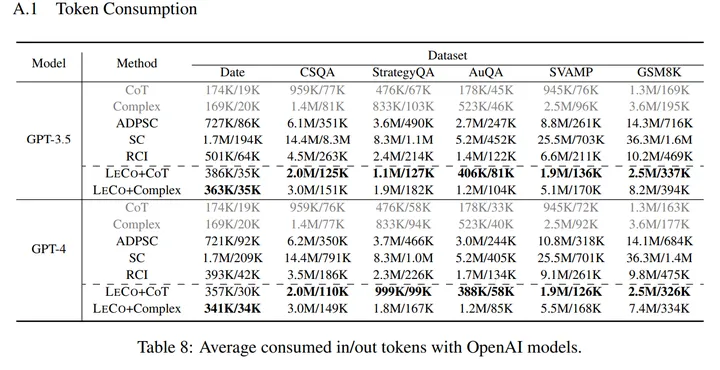
表 3:LeCo 和不同方法的 Token 消耗比较
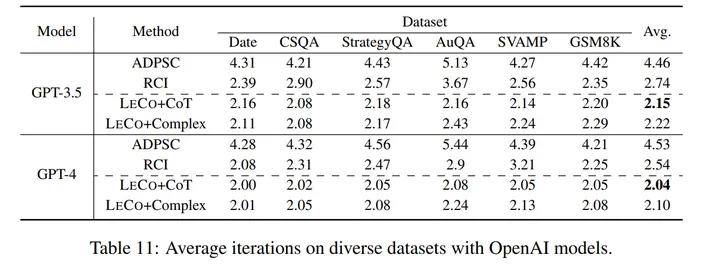
表 4:LeCo 和不同方法的迭代次数比较
人工分析:为了进一步验证 LeCo 是否真的能识别到推理中正确的步骤,本文人工标注了 100 题 GSM8K,找出推理过程中正确和错误的时间步。Exact Correct 表示 LeCo 能精确定位到第一步犯错的步骤,Partial Correct 表示定位在 1 步的误差范围内,Wrong 表示定位误差范围大于 1 步。总体来说,LeCo 可以通过计算置信度的方式而无需外部信息较为准备地找出正确和错误的步骤,不过仍然存在提升空间。
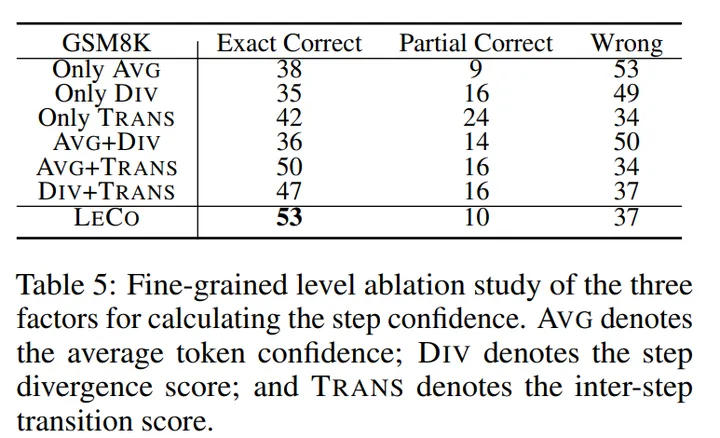
表 5:不同方法计算推理步骤置信度的准确率(人工分析 100 题)
总结
1. 本文提出了一种新的多步推理范式,称为从正确中进行学习(LeCo),通过逐步积累正确步骤接近最终答案;
2. 本文挑战了高质量反馈只能来自外部的观点,并提出了一种仅仅使用模型自身的 confidence score 来近似每个推理步骤的正确性的方法;
3. 无论是开源和闭源模型,都可以在各种多步推理任务中从 LeCo 中获益,同时减少 token 和迭代轮次的消耗。更令人振奋的是,和我们的题目一样,LeCo 消除了 rethink 阶段重新编写 prompt 的需求。





































