在深度学习中,求导几乎是所有优化算法的关键步骤,但是对于单个值的求导比较简单,但是如果对于模型训练过程中每次都需要手动求导就很麻烦,因此深度学习框架都提供了自动导数(自动微分)。

1、PyTorch自动微分
对函数 y = 2X^X 求导(其中X为列向量,这里表示两段列向量做矩阵乘法),其中PyTorch自动微分的代码如下:
import torch
x = torch.arange(4.0)
print("x: ", x)
x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True)
print("x.grad: ", x.grad)
y = 2 * torch.dot(x, x)
print("y: ", y)
y.backward()
print("x.grad: ", x.grad)1、先给x赋值 tensor([0., 1., 2., 3.]) ;2、将x设置为自动微分 ;3、赋值y表达式,计算y的值,结果:tensor(28., grad_fn=<MulBackward0>);4、y.backward() 调用反向传播函数来自动计算y关于x每个分量的梯度,并打印这些梯度;
输出结果:tensor([ 0., 4., 8., 12.]) 和 y = 4X 的导数是一样的。
2、如何自动微分
自动微分开源实现很多,其中类似 PyTorch 的 API 包括 karpathy 开源的 https://github.com/karpathy/micrograd 和 https://github.com/tinygrad/tinygrad,这里为了简单借鉴 micrograd,重写部分代码实现自动微分。
2.1 前向传播
微分需要支持多个基础运算,如+,-,*,/,power等,代码如下:
class Value:
def __init__(self, data, _children=(), _op=''):
self.data = data
self.grad = 0
self._prev = set(_children)
self._op = _op
def __add__(self, other):
other = other if isinstance(other, Value) else Value(other)
out = Value(self.data + other.data, (self, other), '+')
return out
def __mul__(self, other):
other = other if isinstance(other, Value) else Value(other)
out = Value(self.data * other.data, (self, other), '*')
return out
def __pow__(self, other):
assert isinstance(other, (int, float)), "only supporting int/float powers for now"
out = Value(self.data**other, (self,), f'**{other}')
return out
def relu(self):
out = Value(0 if self.data < 0 else self.data, (self,), 'ReLU')
return out
def __neg__(self): # -self
return self * -1
def __radd__(self, other): # other + self
return self + other
def __sub__(self, other): # self - other
return self + (-other)
def __rsub__(self, other): # other - self
return other + (-self)
def __rmul__(self, other): # other * self
return self * other
def __truediv__(self, other): # self / other
return self * other**-1
def __rtruediv__(self, other): # other / self
return other * self**-1
def __repr__(self):
return f"Value(data={self.data}, grad={self.grad})"那么表达式 a * b + c + d**2,按照赋值变量的运行:
a = Value(2.0)
b = Value(-3.0)
c = Value(10.0)
d = Value(2.0)
d = a * b + c
z = d + f**2
print("z: ", z)结果:Value(data=8.0, grad=0),同时按照前向传播路径画图如下:
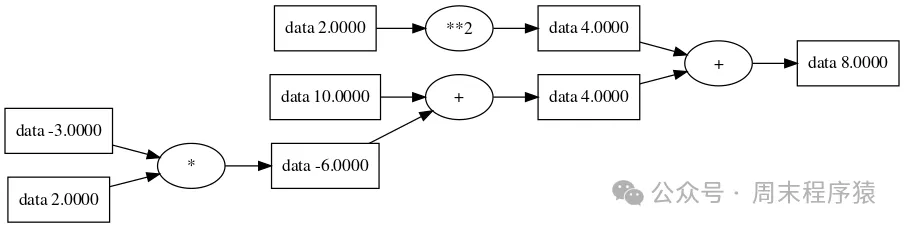 前向传播
前向传播
2.2 反向传播
在反向传播的过程,本质是求网络的每个参数关于最终损失函数的梯度,而该梯度可以成是回传的全局梯度和局部梯度之乘。
其中梯度代表了当前层参数的变化,对最终预测损失的影响(变化率),而该变化率实际取决于当前层参数对下一层输入的影响,以及下一层输入对最终预测损失的影响,两个变化一乘,就是当前层参数对最终预测损失的影响。
那么反向传播的代码实现就是要将每个变量与表达式的结果关联,根据微积分的链式法则(https://zh.wikipedia.org/wiki/%E9%93%BE%E5%BC%8F%E6%B3%95%E5%88%99),如果变量 z 依赖于变量 y,而变量 y 又依赖于变量 x(即 y 和 z 是因变量),那么 z 也通过中间变量 y 来依赖于 x,其中 c = 2 * a; d = c + b; 推倒如下:
c = 2 * a
d = c + b
求导数 dd/da 可以根据微分传递性转换 dd/dc * dc/da
那么 dd/dc = 1(加法的导数是常数),dc/da = 2(乘法的导数对应是2),所以 dd/da = 2根据前向传播的代码添加反向传播:
class Value:
def __init__(self, data, _children=(), _op=''):
self.data = data
self.grad = 0
self._backward = lambda: None
self._prev = set(_children)
self._op = _op
def __add__(self, other):
other = other if isinstance(other, Value) else Value(other)
out = Value(self.data + other.data, (self, other), '+')
def _backward():
self.grad += out.grad
other.grad += out.grad
out._backward = _backward
return out
def __mul__(self, other):
other = other if isinstance(other, Value) else Value(other)
out = Value(self.data * other.data, (self, other), '*')
def _backward():
self.grad += other.data * out.grad
other.grad += self.data * out.grad
out._backward = _backward
return out
def __pow__(self, other):
assert isinstance(other, (int, float)), "only supporting int/float powers for now"
out = Value(self.data**other, (self,), f'**{other}')
def _backward():
self.grad += (other * self.data**(other-1)) * out.grad
out._backward = _backward
return out
def relu(self):
out = Value(0 if self.data < 0 else self.data, (self,), 'ReLU')
def _backward():
self.grad += (out.data > 0) * out.grad
out._backward = _backward
return out
def backward(self):
topo = []
visited = set()
def build_topo(v):
if v not in visited:
visited.add(v)
for child in v._prev:
build_topo(child)
topo.append(v)
build_topo(self)
self.grad = 1
for v in reversed(topo):
v._backward()其中 backward 遍历所有孩子节点,然后 reversed 计算每个_backward,那么表达式 a * b + c + d**2,按照赋值变量的运行:
a = Value(2.0)
b = Value(-3.0)
c = Value(10.0)
f = Value(2.0)
d = a * b + c
z = d + f**2
z.backward()
print("a: ", a.grad)结果:a:-3.0,同时按照反向传播路径画图如下:
 反向传播
反向传播
3、总结
以上就是构造自动微分的代码,功能比较简单,主要是理解梯度的计算方法,并计算各个计算变量在图节点上的关系。