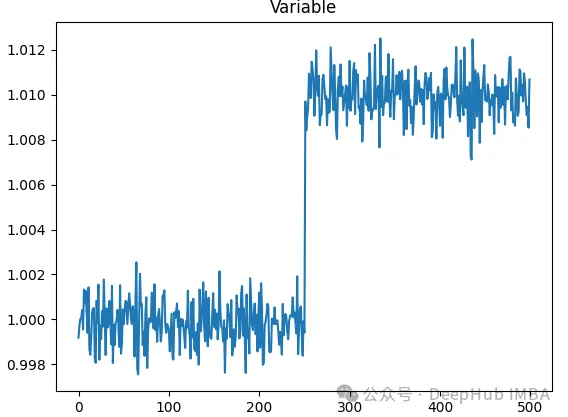
平稳性是时间序列分析与预测的核心概念。在平稳条件下,时间序列的统计特性(如均值)在时间维度上保持不变,仅存在随机波动。
但是实际数据集中很少观察到完全的平稳性。时间序列通常会经历结构性断裂或变化。这些变化会引入非平稳性,从而改变时间序列的整体分布,这些标志着变化开始的时间点被称为变化点。
在时间序列分析和预测中,准确检测结构变化至关重要。新出现的分布模式往往会导致历史数据失去代表性,进而影响基于这些数据训练的模型的有效性。因此需要采用最新数据更新模型或采取其他适当策略。对于历史数据中的变化点,可以通过特征工程方法(如干预分析)进行处理。
但需要注意的是,结构变化与异常值是两个不同的概念。异常值是指与时间序列的基本结构或分布所定义的正常行为显著偏离的观测值。而变化点则是指时间序列的整体结构发生转变,导致分布特性的改变。
接下来,我们首先详细探讨不同类型的结构变化。
结构变化的类型
结构变化可以分为多种类型。深入理解这些变化的性质对于选择适当的处理策略至关重要。
水平变化
水平变化主要体现在序列的均值或方差上。均值的变化表现为平均水平的移动,可以是永久性的,也可以是暂时性的。
永久性水平移动是指序列的平均值永久性地转移到一个新的水平。例如当一家零售企业开设新店时,销售时间序列可能会转移到一个更高的水平,反映出扩大的客户基础。
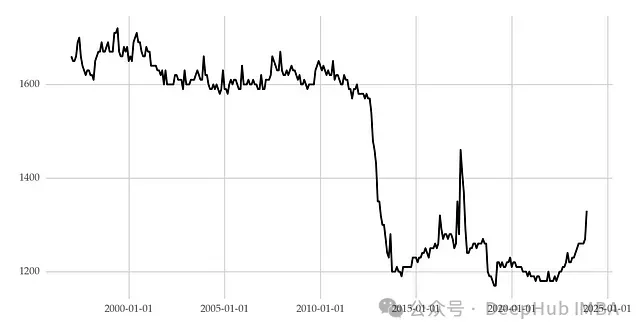
暂时性水平移动是指平均值在一段时间后恢复到原有水平。例如制造工厂的一台机器因维修而临时停机,生产时间序列在维修期间会出现暂时性的低值。一旦机器恢复运行,生产水平预计会回到正常状态。
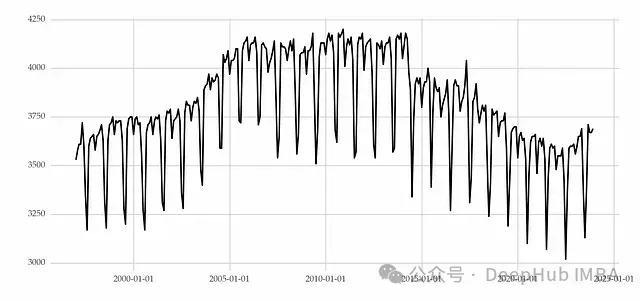
方差变化
方差的变化会导致时间序列离散程度的增加或减少,具有非恒定方差的时间序列通常被称为异方差序列。方差的变化同样可以是永久性的或暂时性的。

方差的周期性变化是波动聚类现象的典型特征。波动聚类指的是时间序列呈现出低方差期和高方差期交替出现的模式。换言之,大(小)幅度变化往往会连续出现。
以下是表示每小时风速变化的时间序列示例,展示了波动聚类现象:
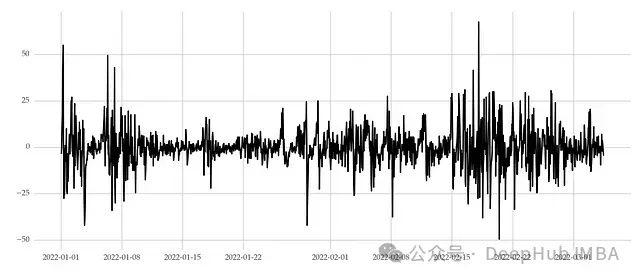
具有波动聚类特征的时间序列示例。
波动聚类在气象学(如风速分析)和金融学(如资产价格研究)等领域中较为常见。
基于Python的变化点检测代码实现
变化点检测算法旨在精确识别时间序列分布发生显著变化的时间点。本节将详细探讨多种变化点检测方法的实际应用。
我们从 datasetsforecast 库中加载一个示例时间序列数据:
from datasetsforecast.m4 import M4
dataset, *_ = M4.load('./data', 'Monthly')
series = dataset.query(f'unique_id=="M1430"').reset_index(drop=True)
series['time'] = pd.date_range(end='2023-12-01', periods=series.shape[0], freq='M')此数据集是非常有名的销量预测比赛M4
利用kats进行变化点检测
kats是Meta开发的一个功能强大的时间序列分析库。它提供了多种变化检测方法,包括CUSUM(累积和)和贝叶斯在线变化点检测等。
kats要求使用特定的数据结构,可以按以下方式进行设置:
from kats.consts import TimeSeriesData
ts = TimeSeriesData(df=series[['time', 'y']])CUSUM(累积和)是一种广泛应用于检测时间序列均值变化的方法。其原理是计算相对于预期值的偏差累积和。如果序列的均值保持稳定,累积和将呈现围绕零的随机波动。累积和的持续正向(或负向)变化则表明均值发生了上升(或下降)移动。
以下代码展示了如何使用kats中的CUSUM方法:
from kats.tests.detectors.test_cusum_detection import CUSUMDetector
model = CUSUMDetector(ts)
change_points = model.detector(direction=['decrease', 'increase'])
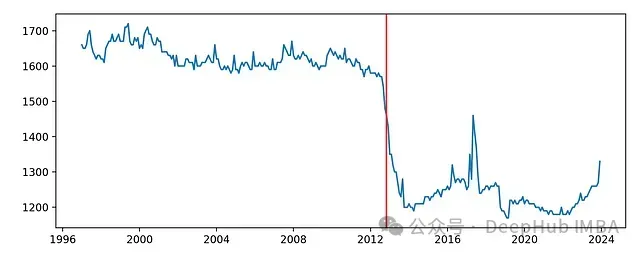
model.plot(change_points)detector方法的 direction 参数用于指定需要监测的变化方向。在本例中我们同时监测序列的上升和下降变化。
CUSUM方法实现了对变化点的准确检测:
另一种与CUSUM相似的方法是在移动平均的基础上计算z分数。kats中的 RobustStatDetector 就采用了这种方法:
from kats.tests.detectors.test_robust_stat_detection import RobustStatDetector
model = RobustStatDetector(ts)
change_points = model.detector(p_value_cutoff=0.001, comparison_window=12)
model.plot(change_points)在这个方法中,我们将p值阈值设置为0.001,窗口大小设置为12(对应于一年的数据,因为该序列是按月收集的)。
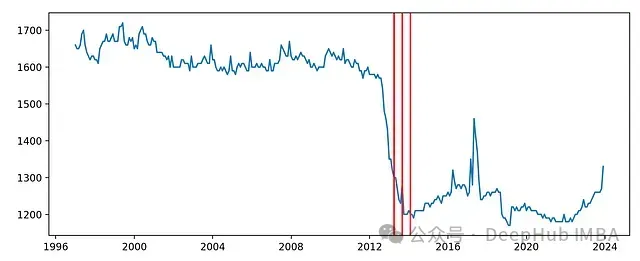
使用kats中的RobustStatDetector检测变化点。RobustStatDetector在这个例子中检测到了几个相互靠近的变化点。
利用ruptures进行变化点检测
ruptures库同样提供了多种变化点检测算法的实现,包括PELT(修剪精确线性时间)、基于核的算法和动态规划算法等。
以下是使用PELT算法检测均值变化的示例:
import ruptures as rpt
# 将时间序列转换为numpy数组
signal = series['y'].values
# 拟合PELT模型
model = rpt.Pelt(model="rbf").fit(signal)
# 获取变化点
result = model.predict(pen=10)PELT算法的核心思想是将时间序列分割成具有不同统计特性(如均值)的多个片段。它通过最小化一个用户定义的成本函数来实现这一目标,该函数的具体形式取决于需要检测的变化类型。在这个例子中我们使用了基于径向基函数的模型(model="rbf")。
以下是PELT模型的检测结果:

变化点的处理策略
在识别出变化点后,下一步就是采取适当的处理措施。以下是几种常用的处理方法:
差分法
对时间序列进行差分是处理均值变化的一种有效方法。这种技术通过计算连续观测值之间的差值来稳定序列的平均水平。
以下是示例序列的一阶差分结果:

差分法能够有效消除许多类型的非平稳性,使得后续的分析和建模工作更加可靠。
虚拟变量法
另一种处理变化点的方法是引入虚拟变量。这种方法在变化点之前赋值为0,之后赋值为1,从而在模型中显式地表示结构变化。
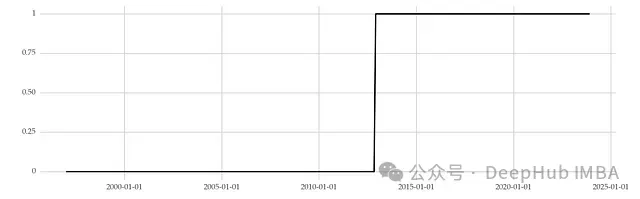
虚拟变量法允许模型捕捉变化前后的不同行为,提高了模型的灵活性和准确性。
区制转换模型
对于暂时性变化,区制转换模型(regime-switching)是一种较为复杂但有效的建模方法。这类模型能够根据当前的状态或区制采用不同的参数设置。
阈值自回归(TAR)模型是区制转换模型的一个典型例子。TAR模型对不同范围的时间序列值采用不同的参数,从而能够捕捉复杂的非线性动态。
总结结论
通过本文的分析,我们可以得出以下几点重要结论:
- 时间序列常常受到结构变化的影响,这些变化会显著改变序列的统计分布特性。
- 结构变化可能发生在均值或方差上,并且可能是永久性的或暂时性的。准确识别变化的性质对于选择适当的处理方法至关重要。
- 现代统计和机器学习提供了多种变化点检测方法,如CUSUM和PELT算法。这些方法在kats和ruptures等Python库中都有实现,为实践应用提供了便利。
- 对于检测到的变化点,可以采用多种处理策略。差分法和引入虚拟变量是处理均值变化的常用方法,而对于更复杂的情况,可以考虑使用区制转换模型。
- 数据预处理在处理结构变化中扮演着关键角色。合适的预处理不仅可以稳定序列的方差,还能为后续的建模工作奠定基础。
通过深入理解时间序列的结构变化,并灵活运用各种检测和处理方法,分析人员可以显著提高时间序列模型的准确性和可靠性,为决策提供更有力的支持。