今天给大家分享机器学习中常用的评估指标。

机器学习的评估指标是用于衡量模型在特定任务中的性能,帮助我们判断模型是否在测试集上有效,并指导模型的优化和调整。
评估指标因任务的不同而有所区别,常见的任务包括分类、回归等。
分类问题评估指标
分类问题是指将输入样本分类为某个离散标签的任务。
常见的评估指标有以下几种。
1.混淆矩阵
顾名思义,混淆矩阵给出一个 N*N 矩阵作为输出,其中 N 是目标类的数量。
混淆矩阵是分类器做出的正确和错误预测数量的表格总结。
该矩阵将实际值与机器学习模型的预测值进行比较。
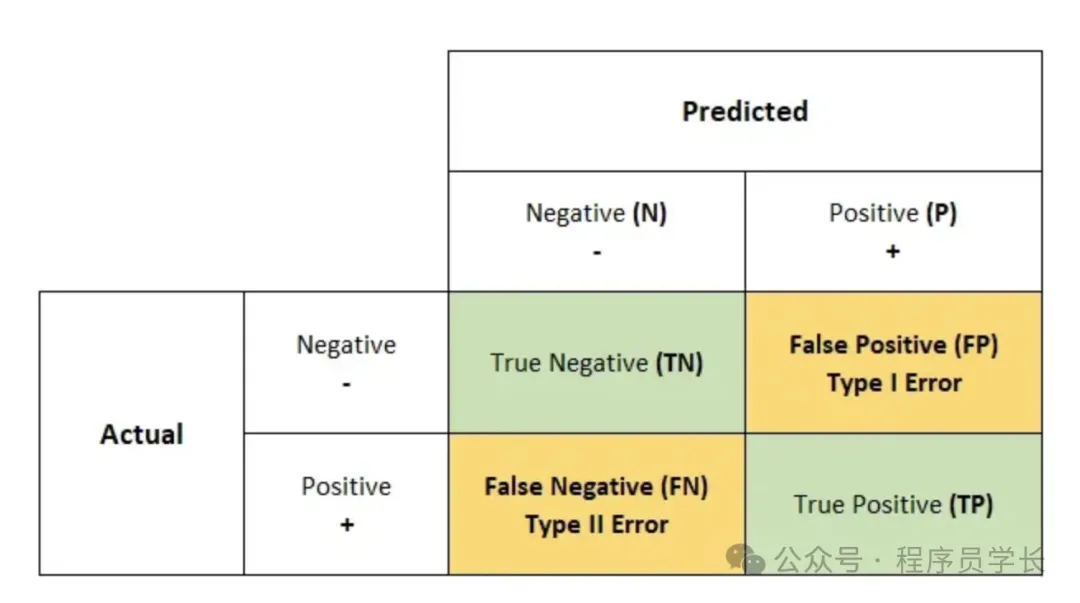
- 真正例(True Positive, TP):模型正确预测为正例的数量。
- 假正例(False Positive, FP):模型错误预测为正例的数量。
- 真负例(True Negative, TN):模型正确预测为负例的数量。
- 假负例(False Negative, FN):模型错误预测为负例的数量。
2.准确率 (Accuracy)
准确率是指模型预测正确的样本数占总样本数的比例。
公式
适用场景
当各类别样本数量较为均衡时,准确率是一个好的评估指标。
from sklearn.metrics import accuracy_score
y_true = [0, 1, 0, 1]
y_pred = [0, 0, 0, 1]
accuracy = accuracy_score(y_true, y_pred)
print("Accuracy:", accuracy)3.精确率 (Precision)
精确率是指被模型预测为正类的样本中,真正为正类的比例。
公式
适用场景
当误将负类预测为正类的代价较高时(如垃圾邮件分类)。
from sklearn.metrics import precision_score
y_true = [0, 1, 0, 1]
y_pred = [0, 0, 0, 1]
precision = precision_score(y_true, y_pred)
print("Precision:", precision)4.召回率 (Recall)
召回率是指正类样本中被模型正确预测为正类的比例。
公式
适用场景
当误将正类预测为负类的代价较高时(如疾病检测)。
from sklearn.metrics import recall_score
y_true = [0, 1, 0, 1]
y_pred = [0, 0, 0, 1]
recall = recall_score(y_true, y_pred)
print("Recall:", recall)5.特异性
特异性是分类模型对负类样本的识别能力的度量,它表示所有真实为负类的样本中,模型正确识别为负类的比例。
公式
from sklearn.metrics import confusion_matrix
y_true = [0, 1, 0, 1]
y_pred = [0, 0, 0, 1]
tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel()
specificity = tn / (tn + fp)
print("Specificity:", specificity)6.F1-Score
F1-Score 是精确率和召回率的调和平均,用于平衡两者之间的影响。
适用场景
当需要在精确率和召回率之间找到平衡点时,使用 F1-Score。
from sklearn.metrics import f1_score
y_true = [0, 1, 0, 1]
y_pred = [0, 0, 0, 1]
f1 = f1_score(y_true, y_pred)
print("F1 Score:", f1)7.AUC-ROC
AUC (Area Under the Curve) 表示 ROC 曲线下的面积,AUC 越高,模型越好。下图显示了 ROC 曲线,y 轴为 TPR(真阳性率),x 轴为 FPR(假阳性率)。

回归问题评估指标
回归问题的目标是预测连续值,常见的评估指标有以下几种。
1.均方误差 (MSE)
MSE 是预测值与真实值之间差异的平方的平均值,常用于衡量模型的预测误差。
适用场景
对大误差比较敏感的场景,因为误差平方放大了大的偏差。
from sklearn.metrics import mean_squared_error
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
mse = mean_squared_error(y_true, y_pred)
print("Mean Squared Error (MSE):", mse)2. 均方根误差 (RMSE)
RMSE是 MSE 的平方根,用于衡量预测误差的平均幅度。
RMSE 的单位与原始预测变量相同,因此便于理解。
from sklearn.metrics import mean_squared_error
import numpy as np
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
mse = mean_squared_error(y_true, y_pred)
rmse = np.sqrt(mse)
print("Root Mean Squared Error (RMSE):", rmse)3. 平均绝对误差 (MAE)
MAE 是预测值与真实值之间差异的绝对值的平均值,衡量模型预测误差的平均大小。
适用场景
对所有误差同等看待的场景。
from sklearn.metrics import mean_absolute_error
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
mae = mean_absolute_error(y_true, y_pred)
print("Mean Absolute Error (MAE):", mae)4. R方值
R² 表示模型解释了目标变量总变异的比例,取值范围为 0到1,数值越大表示模型越好。
适用场景
适用于评估回归模型的整体性能。
from sklearn.metrics import r2_score
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
r2 = r2_score(y_true, y_pred)
print("R-squared (R^2):", r2)5.调整后的 R²
调整后的 是在 的基础上引入了对模型复杂度的惩罚,考虑了模型中自变量的数量。
其公式为
其中:
- n 是样本数量。
- p 是模型中的自变量(特征)数量。
from sklearn.metrics import r2_score
def adjusted_r2(r2, n, k):
return 1 - (1 - r2) * (n - 1) / (n - k - 1)
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
r2 = r2_score(y_true, y_pred)
n = len(y_true) # Number of observations
k = 1 # Number of predictors
adj_r2 = adjusted_r2(r2, n, k)
print("Adjusted R-squared:", adj_r2)






































