特征重要性是解释机器学习模型最常用的工具。这导致我们常常认为特征重要性等同于特征好坏。
事实并非如此。
当一个特征很重要时，它仅仅意味着模型发现它在训练集中很有用。但是，这并不能说明该特征在新数据上的泛化能力！。
为了说明这一点，我们需要区分两个概念：
- 预测贡献：变量在模型预测中的权重。这是由模型在训练集中发现的模式决定的。这相当于特征重要性。
- 错误贡献：模型在暂存数据集上的错误中，变量所占的权重。这可以更好地反映特征在新数据上的表现。
在本文中，我将解释在分类模型中计算这两个量背后的逻辑。我还将举例说明在特征选择中使用 "误差贡献 "比使用 "预测贡献" 会得到更好的结果。
假设我们有一个分类问题，想要预测一个人的收入是低于还是高于 10k。还假设我们已经有了模型的预测结果：
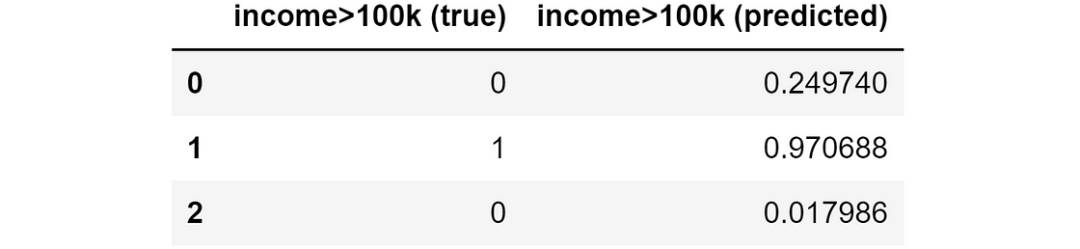实际值和模型预测
预测和误差贡献的计算主要基于模型对每个个体的误差以及每个个体的 SHAP 值。因此，我们必须花一点时间来讨论两个相关问题：
- 分类模型应该使用哪种 "误差"？
- 我们应该如何管理分类模型中的 SHAP 值？
我将在接下来的两段中讨论这些问题。
在分类模型中使用哪种 "误差"？
我们的主要目标是计算模型中每个特征的误差贡献（Error Contribution）。因此，最重要的问题是：如何定义分类模型中的 "误差"？
请注意，我们需要一个可以在个体水平上计算的误差，然后将其汇总到整个样本中，得到一个 "平均误差"（回归模型的绝对误差请看👉颠覆认知！这个特征很重要，但不是个好特征！）。
分类模型最常用的损失函数是对数损失（又名交叉熵）。它是否适合我们。
下面是对数损失的数学公式：
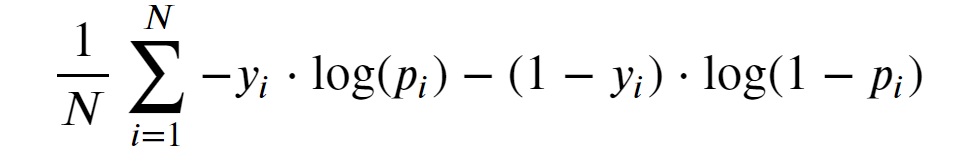图片
对数损失似乎是最佳选择，因为
- 公式的外部部分只是一个简单的平均值；
- "损失"，顾名思义意思是越小越好（就像 "误差"）。
试着理解一下，为什么我们可以称它为 "误差"。为了简单起见，把注意力集中在和里面的数量上：
图片
这是单个个体对全局对数损失的贡献，因此我们可以称之为 "个体对数损失"。
这个公式看起来仍然很吓人，但如果我们考虑到，在二元分类问题中，y只能是 0 或 1，我们就可以得到一个更简单的版本：
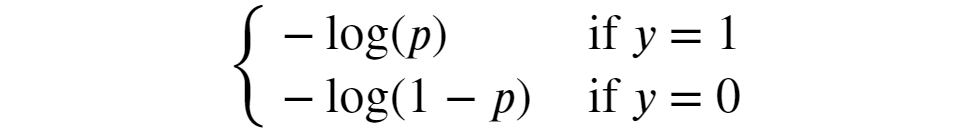图片
一图胜千言，现在就很容易理解对数损失背后的主要思想了。
图片
预测概率与真实值（无论是 0 还是 1）相差越远，损失就越大。此外，如果预测值与真实值相差很远（例如，p=.2，y=1 或 p=.8，y=0），那么损失就会比比例损失更严重。现在我们应该更清楚为什么对数损失实际上是一种误差了。
我们准备将单个对数损失公式转化为一个 Python 函数。
为了避免处理无限值（当 y_pred 恰好为 0 或 1 时会出现这种情况），我们将使用一个小技巧：如果 y_pred 与 0 或 1 的距离小于 ε，我们将其分别设置为 ε 或 1-ε。对于 ε，我们将使用 1^-15（这也是 Scikit-learn 使用的默认值）。
def individual_log_loss(y_true, y_pred, eps=1e-15):
"""Compute log-loss for each individual of the sample."""
y_pred = np.clip(y_pred, eps, 1 - eps)
return - y_true * np.log(y_pred) - (1 - y_true) * np.log(1 - y_pred)我们可以使用该函数计算数据集中每一行的单个对数损失：
目标变量、模型预测以及由此产生的个体对数损失
可以看出，个体 1 和个体 2 的对数损失（或误差）非常小，因为预测值都非常接近实际观测值，而个体 0 的对数损失较高。
如何管理分类模型中的 SHAP 值？
最流行的模型是基于树的模型，如 XGBoost、LightGBM 和 Catboost。在数据集上获取基于树的分类器的 SHAP 值非常简单：
from shap import TreeExplainer
shap_explainer = TreeExplainer(model)
shap_values = shap_explainer.shap_values(X)
# 可以定义一个函数来获取
def get_preds_shaps(df, features, target, ix_trn):
"""Get predictions (predicted probabilities) and SHAP values for a dataset."""
model = LGBMClassifier().fit(df.loc[ix_trn, features], df.loc[ix_trn, target])
preds = pd.Series(model.predict_proba(df[features])[:,1], index=df.index)
shap_explainer = TreeExplainer(model)
shap_expected_value = shap_explainer.expected_value[-1]
shaps = pd.DataFrame(
data=shap_explainer.shap_values(df[features])[1],
index=df.index,
columns=features)
return preds, shaps, shap_expected_value例如，我们计算了该问题的 SHAP 值，得到了如下结果：
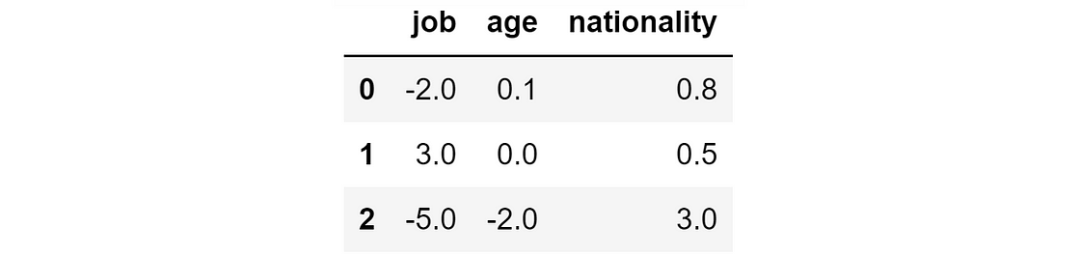模型预测的 SHAP 值
不过，就本文而言，只要知道以下几点就足够了：
- SHAP 正值：该特征导致该个体的概率增加；
- SHAP 负值：该特征导致该个体的概率降低。
因此，很明显，个体的 SHAP 值总和与模型的预测之间存在直接关系。
然而，由于 SHAP 值可以是任何实际值（正值或负值），我们不能期望它等于对该个体的预测概率（即介于 0 和 1 之间的数字）。那么，SHAP 值总和与预测概率之间的关系是什么呢？
由于 SHAP 值可以是任何负值或正值，因此我们需要一个函数来将 SHAP 和转化为概率。这个函数必须具备两个特性
- 它应将任何实数值 "挤入" 区间 [0,1]；
- 它应该是严格递增的（因为较高的 SHAP 和总是与较高的预测值相关联）。
符合这些要求的函数就是 sigmoid 函数。因此，模型对某一行预测的概率等于该个体 SHAP 值总和的正余弦值。
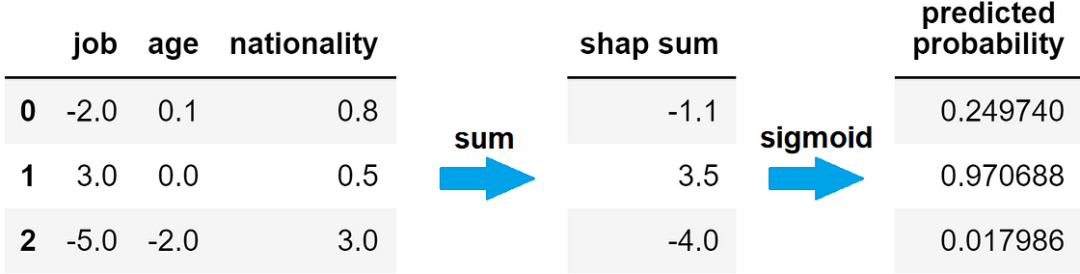从 SHAP 值到预测概率
下面是 sigmoid 函数的样子：
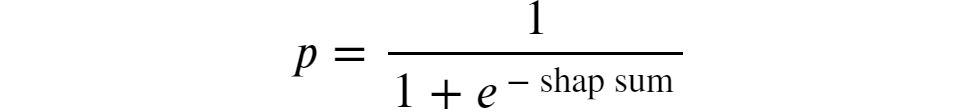图片
那么，把这个公式转换成一个 Python 函数：
def shap_sum2proba(shap_sum):
"""Compute sigmoid function of the Shap sum to get predicted probability."""
return 1 / (1 + np.exp(-shap_sum))还可以用图形显示出来，看看我们的个体在曲线上的位置：
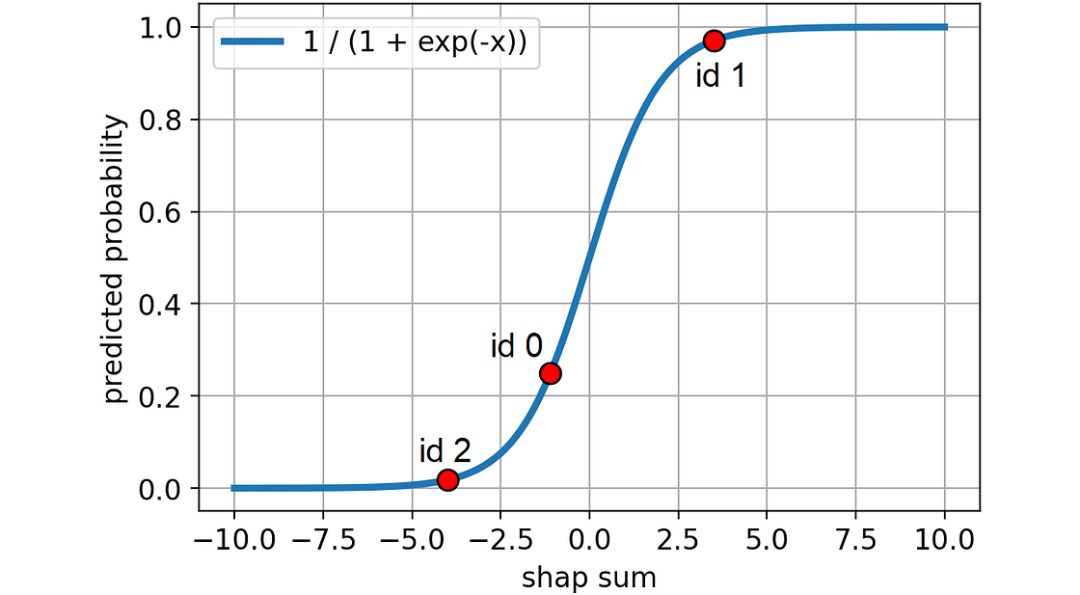图片
既然我们已经了解了在分类问题中应该使用哪种误差以及如何处理 SHAP 值，那么我们就可以看看如何计算预测值和误差贡献值了。
计算 "预测贡献"
当 SHAP 值为高度正值（高度负值）时，预测结果会比没有该特征时高（低）得多。换句话说，如果 SHAP 值的绝对值很大，那么该特征就会对最终预测结果产生很大影响。
这就是为什么我们可以通过取某一特征的 SHAP 绝对值的平均值来衡量该特征的预测贡献。
prediction_contribution = shap_values.abs().mean()在玩具数据集中，就得到了这样的结果：
预测贡献
因此，就特征的重要性而言，job是主要特征，其次是nationality，然后是age。
但误差贡献率如何呢？
5. 计算 "误差贡献"
"误差贡献" 背后的理念是计算如果我们去掉一个给定的特征，模型的误差会是多少。
有了 SHAP 值，回答这个问题就很容易了：如果我们从 SHAP 总和中剔除某个特征，就可以得到模型在不知道该特征的情况下会做出的预测。但这还不够：正如我们所看到的，要获得预测概率，我们首先需要应用 sigmoid 函数。
因此，我们首先需要从 SHAP 总和中减去某个特征的 SHAP 值，然后再应用 sigmoid 函数。这样，我们就得到了模型在不知道这些特征的情况下的预测概率。
在 Python 中，我们可以一次性完成所有特征的预测：
y_pred_wo_feature = shap_values.apply(lambda feature: shap_values.sum(axis=1) - feature).applymap(shap_sum2proba)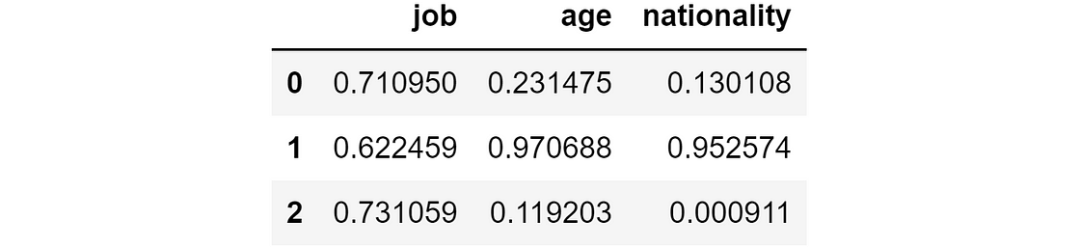
如果删除相应特征，将得到的预测结果
这意味着，如果没有job这一特征，模型预测第一个人的概率为 71%，第二个人的概率为 62%，第三个人的概率为 73%。相反，如果我们没有nationality这一特征，预测结果将分别为 13%、95% 和 0%。
根据我们移除的特征，预测的概率相差很大。因此，得出的误差（个体对数损失）也会大不相同。
我们可以使用上面定义的函数（"individual_log_loss"）来计算没有相应特征时的个体对数损失：
ind_log_loss_wo_feature = y_pred_wo_feature.apply(lambda feature: individual_log_loss(y_true=y_true, y_pred=feature))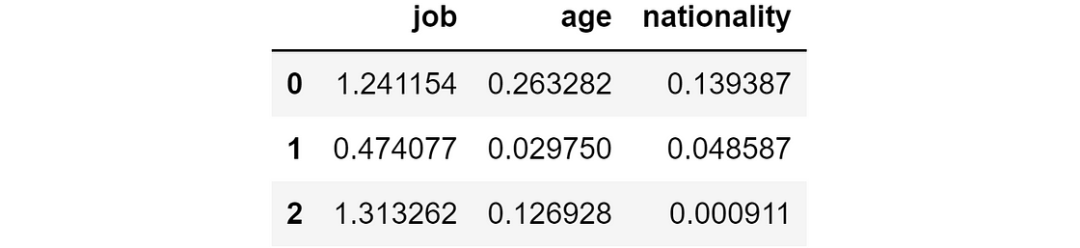
如果删除相应特征，我们将获得的单个对数损失
例如，如果我们选取第一行，我们可以看到，如果没有job特征，对数损失将为 1.24，但如果没有nationality特征，对数损失仅为 0.13。由于我们要尽量减少损失，在这种情况下，最好是去掉nationality这个特征。
现在，要知道有或没有该特征的模型会更好，我们可以计算完整模型的单个对数损失与没有该特征的单个对数损失之间的差值：
ind_log_loss = individual_log_loss(y_true=y_true, y_pred=y_pred)
ind_log_loss_diff = ind_log_loss_wo_feature.apply(lambda feature: ind_log_loss - feature)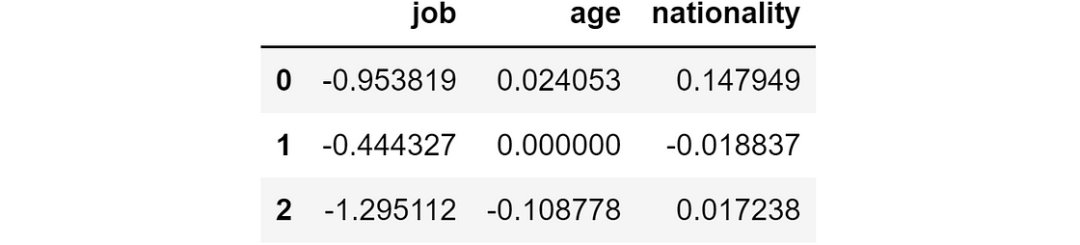
模型误差与没有该特征时的误差之差
如果这个数字是
- 负数，则该特征的存在会导致预测误差减小，因此该特征对该观测结果非常有效。
- 正数，则该特征的存在会导致预测误差增大，因此该特征对该观测结果不利。
最后，我们可以按列计算出每个特征的误差贡献值，即这些值的平均值：
error_contribution = ind_log_loss_diff.mean()
错误贡献
一般来说，如果这个数字是负数，则说明该特征具有积极作用；相反，如果这个数字是正数，则说明该特征对模型有害，因为它往往会增加模型的平均误差。
在这种情况下，我们可以看到，模型中job特征的存在导致个体对数损失平均减少-0.897，而nationality特征的存在导致个体对数损失平均增加 0.049。因此，尽管nationality是第二重要的特征，但它的效果并不好，因为它会使平均个体对数损失增加 0.049。
将以上过程总结一个函数公后续使用：
def get_feature_contributions(y_true, y_pred, shap_values, shap_expected_value):
"""Compute prediction contribution and error contribution for each feature."""
prediction_contribution = shap_values.abs().mean().rename("prediction_contribution")
ind_log_loss = individual_log_loss(y_true=y_true, y_pred=y_pred).rename("log_loss")
y_pred_wo_feature = shap_values.apply(lambda feature: shap_expected_value + shap_values.sum(axis=1) - feature).applymap(shap_sum2proba)
ind_log_loss_wo_feature = y_pred_wo_feature.apply(lambda feature: individual_log_loss(y_true=y_true, y_pred=feature))
ind_log_loss_diff = ind_log_loss_wo_feature.apply(lambda feature: ind_log_loss - feature)
error_contribution = ind_log_loss_diff.mean().rename("error_contribution").T
return prediction_contribution, error_contribution真实数据集示例
具体代码可参考上一篇内容：
下面，我将使用来自Pycaret的数据集。该数据集名为 "Gold"，包含一些金融数据的时间序列。
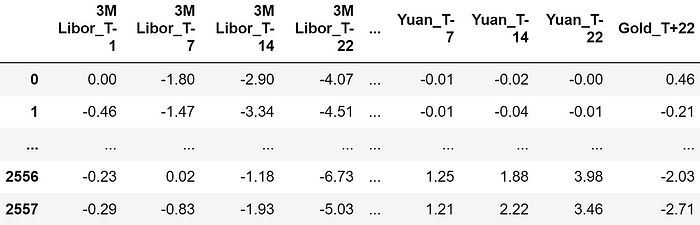数据集样本。特征均以百分比表示，因此 -4.07 表示回报率为 -4.07%
特征包括观察时刻前 22 天、14 天、7 天和 1 天（"T-22"、"T-14"、"T-7"、"T-1"）的金融资产回报率。以下是用作预测特征的所有金融资产：
图片
可用资产列表。每种资产的观测时间分别为-22、-14、-7 和-1。
我们总共有 120 个特征。
我们的目标是预测黄金未来 22 天的回报率是否会大于 5%。换句话说，目标变量是0/1变量的：
- 0，如果黄金未来 22 天的回报率小于 5%；
- 1，如果黄金未来 22 天的回报率大于 5%。
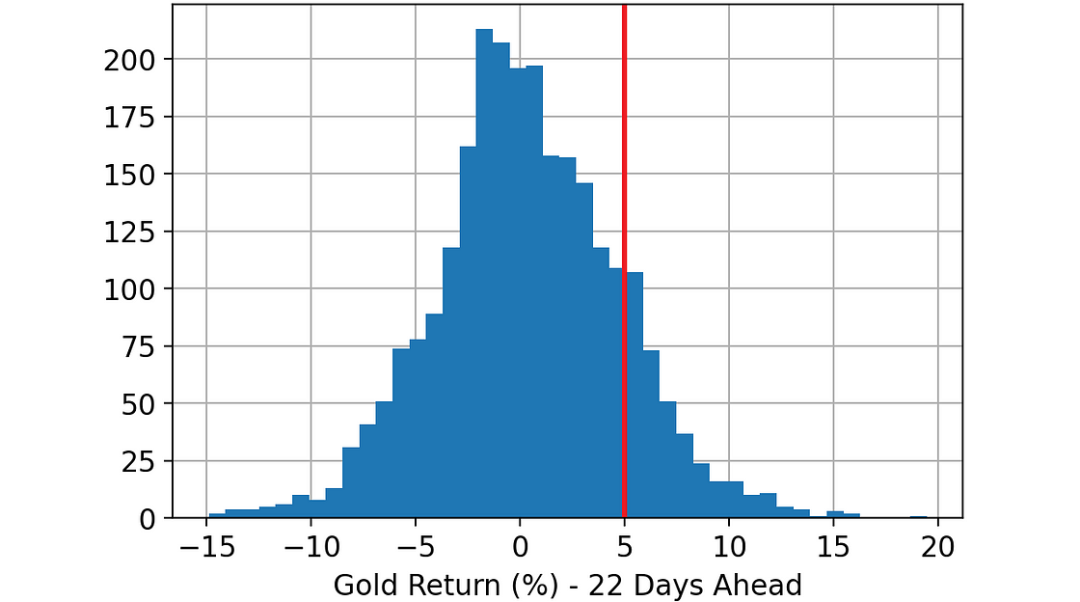图片
未来 22 天黄金回报率柱状图。标为红色的阈值用于定义我们的目标变量：回报率是否大于 5%
加载数据集后，我执行了以下步骤：
- 随机分割整个数据集：33% 的行在训练数据集中，另外 33% 在验证数据集中，剩下的 33% 在测试数据集中。
- 在训练数据集上训练 LightGBM 分类器。
- 使用上一步训练的模型对训练、验证和测试数据集进行预测。
- 使用 Python 库 "shap "计算训练、验证和测试数据集的 SHAP 值。
- 使用我们在上一段中看到的代码，计算每个特征在每个数据集（训练集、验证集和测试集）上的预测贡献值和误差贡献值。
至此，我们就有了预测贡献值和误差贡献值，可以对它们进行比较了：
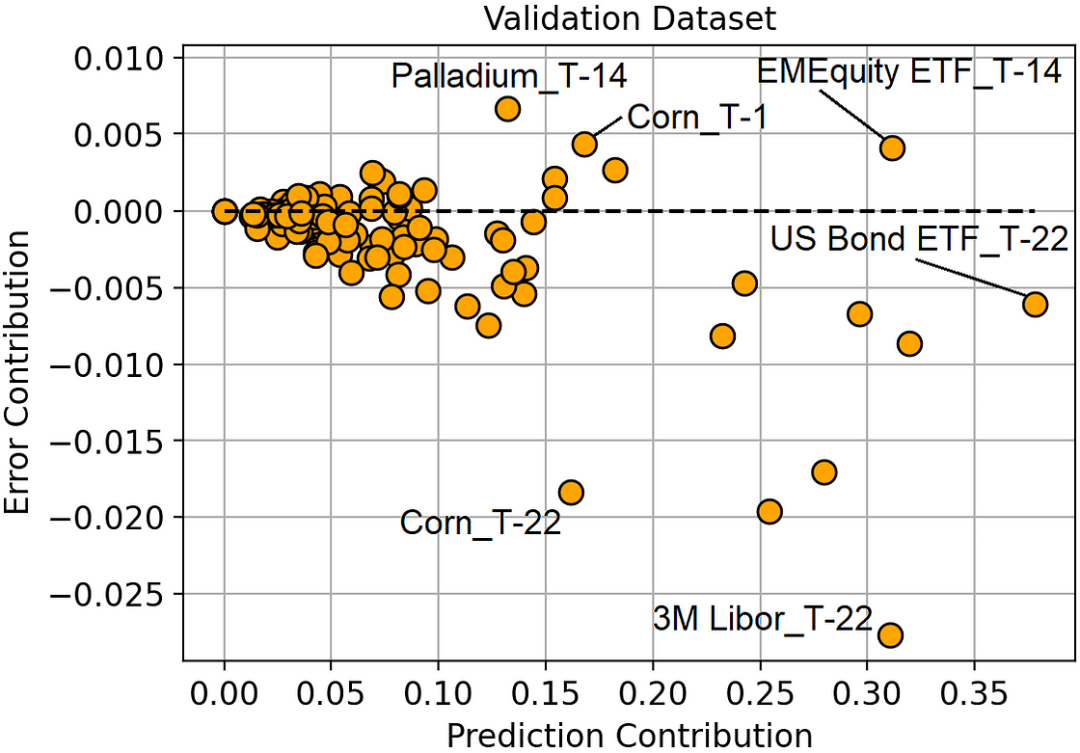预测贡献与误差贡献（验证数据集）
通过观察这幅图，我们可以对模型有宝贵的了解。
最重要的特征是 T-22 天的美国债券 ETF，但它并没有带来如此大的误差减少。最好的特征是 T-22 日的 3M Libor，因为它能最大程度地减少误差。
玉米价格有一些非常有趣的地方。T-1 期和 T-22 期的收益率都是最重要的特征之一，但其中一个特征（T-1 期）是过度拟合的（因为它会使预测误差变大）。
一般来说，我们可以观察到所有误差贡献较大的特征都是相对于 T-1 或 T-14（观察时刻前 1 天或 14 天）而言的，而所有误差贡献较小的特征都是相对于 T-22（观察时刻前 22 天）而言的。这似乎表明，最近的特征容易过度拟合，而较早回报的特征往往概括性更好。
除了深入了解模型之外，我们还可以很自然地想到使用误差贡献来进行特征选择。这就是我们下一段要做的。
"误差贡献"进行递归特征消除
递归特征消除（RFE）是从数据集中逐步去除特征的过程，目的是获得更好的模型。
RFE 算法非常简单：
- 初始化特征列表；
- 使用当前特征列表作为预测因子，在训练集上训练一个模型；
- 从特征列表中删除 "最差 "特征；
- 回到第 2 步（直到特征列表为空）。
在传统方法中，"最差" = 最不重要。然而，根据我们的观察，我们可能会反对先删除危害最大的特征。
换句话说
- 传统的 RFE：先去除最无用的特征（最无用 = 验证集上最低的预测贡献）。
- 我们的 RFE：先去除最有害的特征（最有害 = 验证集上最高的误差贡献）。
为了验证这种直觉是否正确，我使用这两种方法进行了模拟。
这是验证集上的对数损失结果：
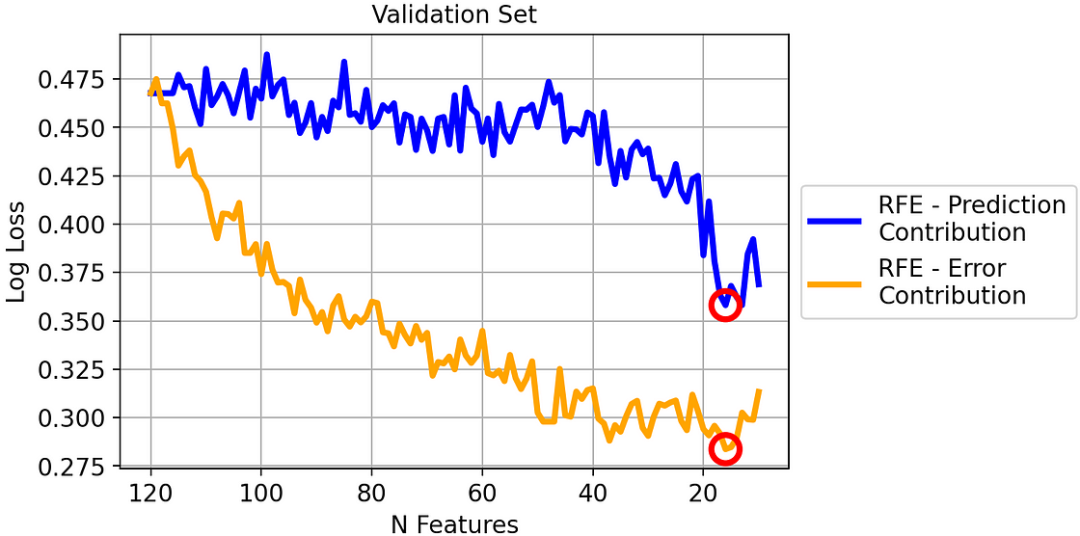两种策略在验证集上的对数损失
由于对数损失是一个 "越低越好 "的指标，我们可以看到，在验证数据集上，我们的 RFE 版本明显优于经典 RFE。
不过，你可能会怀疑，只看验证集并不公平，因为误差贡献是在验证集上计算的。那么，我们来看看测试集。
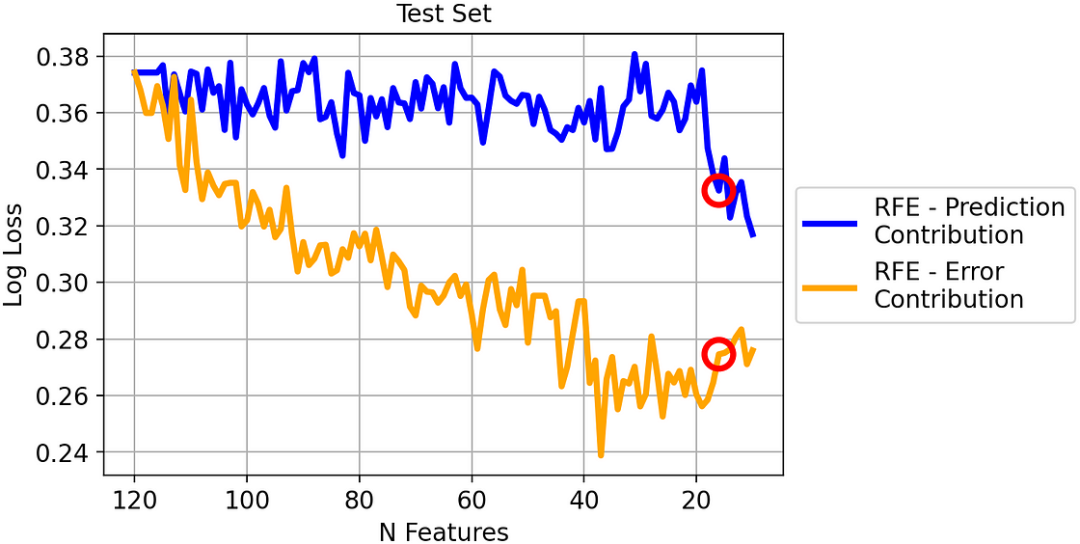两种策略在测试集上的对数损失
即使现在两种方法之间的差距变小了，但我们可以看到差距仍然很大，因此足以得出结论：在这个数据集上，基于误差贡献的 RFE 明显优于基于预测贡献的 RFE。
除了对数损失，我们还可以考虑一种更有实用价值的指标。例如，我们来看看验证集上的平均精度：
两种策略在验证集上的平均精确度
值得注意的是，尽管贡献误差是基于对数损失计算的，但我们在平均精度方面也取得了很好的结果。
如果我们想根据平均精度做出决定，那么我们就会选择验证集上平均精度最高的模型。这意味着：
- 基于误差贡献的 RFE：具有 19 个特征的模型；
- 基于预测贡献的 RFE：具有 14 个特征的模型；
如果我们这样做，在新数据上会观察到什么性能？回答这个问题的最佳代表就是测试集：
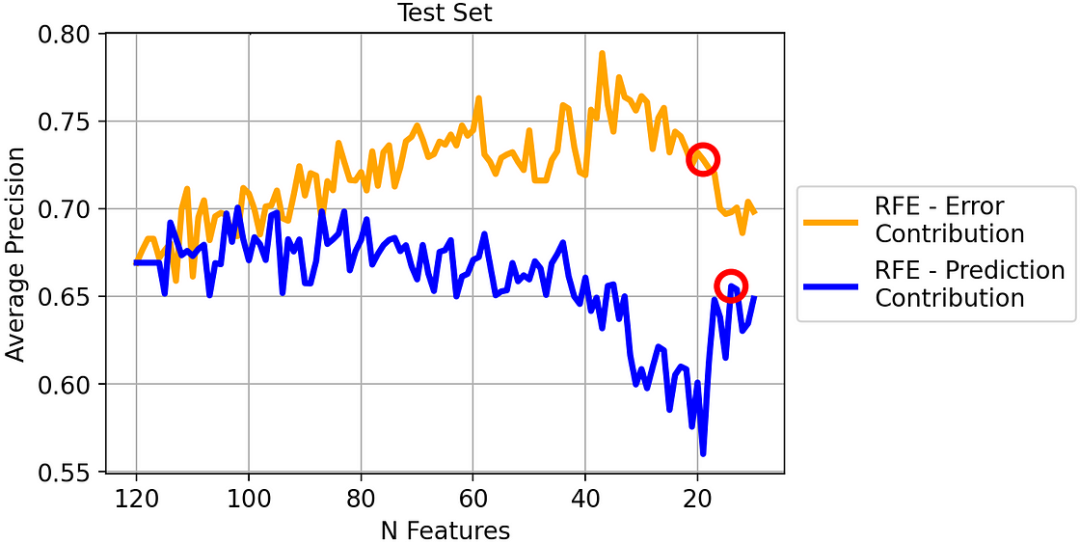图片
两种策略在验证集上的平均精确度
同样在这种情况下，基于误差贡献的 RFE 性能总体上优于基于预测贡献的 RFE。特别是，根据我们之前的判断：
- 基于误差贡献的 RFE（包含 19 个特征的模型）： 平均精确度为 72.8%；
- 基于预测贡献的 RFE（模型有 14 个特征）：平均精度为 65.6%： 平均精度为 65.6%。
因此，通过使用基于误差贡献的 RFE，而不是传统的基于预测贡献的 RFE，我们可以在平均精确度上额外获得 7.2% 的显著提高！
结论
特征重要性的概念在机器学习中扮演着重要角色。然而，"重要性" 的概念常常被误认为是 "好"。
为了区分这两个方面，我们引入了两个概念： 预测贡献和误差贡献。这两个概念都基于验证数据集的 SHAP 值，在文章中我们看到了计算它们的 Python 代码。
我们还在一个真实的金融数据集（其中的任务是预测黄金价格）上对它们进行了尝试，结果证明，与传统的基于预测贡献的 RFE 相比，基于误差贡献的递归特征消除可使平均精度提高 7%。
