译者 | 朱先忠
审校 | 重楼
简介
视觉转换器(Vision Transformer,通常缩写为“ViT”)可以被视为计算机视觉领域的重大突破技术。当涉及到与视觉相关的任务时,人们通常使用基于CNN(卷积神经网络)的模型来解决。到目前为止,这些模型的性能总是优于任何其他类型的神经网络。直到2020年,Dosovitskiy等人发表了一篇题为《一张图顶16×16个单词:大规模图像识别的转换器》的论文(参考文献1),论文中强调这种转换器能够提供比传统卷积神经网络更好的能力。
传统卷积神经网络中的单个卷积层通过使用核提取特征来工作。由于内核的大小与输入图像相比相对较小,因此它只能捕获该小区域内包含的信息。换句话说,它侧重于提取局部特征。为了理解图像的全局上下文,需要使用由多个卷积层组成的一个栈结构。ViT解决了这个问题,因为它实现了直接从初始层捕获全局信息。因此,在ViT中堆叠多个卷积层可以实现更全面的信息提取。

图1:通过堆叠多个卷积层,CNN可以实现更大的感受野,这对于捕捉图像的全局上下文至关重要(参考文献2)
视觉转换器架构
如果你曾经学习过转换器,你应该熟悉编码器和解码器这两个术语。在NLP(自然语言处理)领域,特别是对于机器翻译等任务,编码器负责捕获输入序列中标记(即单词)之间的关系,而解码器负责生成输出序列。在ViT的情况下,我们只需要编码器部分,它将图像的每个图块视为一个标记。基于同样的想法,编码器能够找到图块之间的关系。
整个视觉转换器架构如图2所示。在我们详细讨论有关代码之前,我将先使用以下几小节来解释此架构的每个组件。
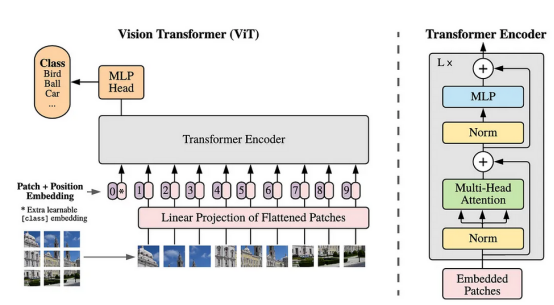
图2:视觉转换器架构(参考文献1)
图块扁平化和线性投影
根据上图,我们可以看到,要做的第一步是将图像划分为图块。所有这些图块排列成一个序列。然后,这些图块中的每一个都被扁平化,每个图块都形成一个一维阵列。然后,通过线性投影将这些标记的序列投影到更高维的空间中。此时,我们可以将投影结果视为NLP中的单词嵌入,即表示单个单词的向量。从技术上讲,线性投影过程可以用简单的MLP(多层感知机)或卷积层来完成。稍后,我将在具体的实施过程中对此进行更多的解释。
类标记和位置嵌入
由于我们正在处理分类任务,我们需要在投影的图块序列前添加一个新的标记。这个标记称为类标记,它将通过为每个图块分配重要性权重来聚合其他图块的信息。值得注意的是,图块扁平化和线性投影会导致模型丢失空间信息。因此,为了解决这个问题,所有标记(包括类标记)都添加了位置嵌入,以便重新引入空间信息。
转换器编码器和MLP头
在这个阶段,张量已经准备好,将被馈送到转换器编码器块中,其详细结构可以在图2的右侧看到。该块由四个部分组成:层规一化、多头注意力、另一层规一化和MLP层。值得注意的是,这里实现了两个残差连接。转换器编码器块左上角的L×表示将根据要构建的模型大小重复L次。
最后,我们将把编码器块连接到MLP头。请记住,要转发的张量只是从类标记部分出来的张量。MLP头部本身由一个完全连接的层和一个输出层组成,其中输出层中的每个神经元代表数据集中一个可用的类。
视觉转换器变体
在原始论文中提出了三种ViT变体,即ViT-B、ViT-L和ViT-H,如图3所示,其中:
- Layers(L):转换器编码器的数量。
- Hidden size(D):嵌入维度以表示单个图块。
- MLP size:MLP隐藏层中的神经元数量。
- Heads:多头注意力层中的注意力头数。
- Params:模型的参数数量。
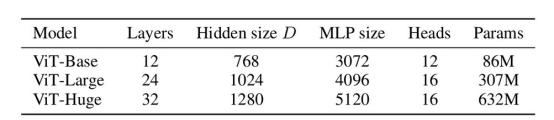
图3:三种视觉转换器变体的详细信息(参考文献1)
在本文中,我想使用PyTorch框架从头开始实现一个ViT-Base架构。顺便说一句,该模块本身实际上还提供了几个预训练的ViT模型(参考文献3),即ViT_b_16、ViT_b_32、ViT_l_16、ViT_l_32和ViT_h_14,其中作为这些模型后缀的数字是指使用的图块大小。
从头开始实现一个ViT
现在,让我们开始真正有趣的部分。实现一个ViT编程首先要做的是导入模块。在这种情况下,我们将只依赖PyTorch框架的功能来构建ViT架构。从torchinfo加载的summary()函数将帮助我们显示模型的详细信息。
# 代码块1
import torch
import torch.nn as nn
from torchinfo import summary参数配置
在代码块2中,我们将初始化几个变量来配置模型。在这里,我们假设单个批次中要处理的图像数量仅为1,其维度为3×224×224(标记为#(1))。我们在这里要使用的变体是ViT-Base,这意味着我们需要将图块大小设置为16,注意头数量设置为12,编码器数量设置为12,嵌入维度设置为768(#(2))。通过使用此配置,图块数量将为196(#(3))。这个数字是通过将大小为224×224的图像划分为16×16个图块而获得的,其中它产生了14×14的网格。因此,一张图像将有196个图块。
我们还将对dropout层使用0.1的速率(#(4))。值得注意的是,论文中没有明确提及dropout层的使用。由于在构建深度学习模型时,使用这些层可以被视为一种标准做法,因此我无论如何都会实现它。我们假设数据集中有10个类,相应地设置了NUM_classes变量。
# 代码块2
#(1)
BATCH_SIZE = 1
IMAGE_SIZE = 224
IN_CHANNELS = 3
#(2)
PATCH_SIZE = 16
NUM_HEADS = 12
NUM_ENCODERS = 12
EMBED_DIM = 768
MLP_SIZE = EMBED_DIM * 4 # 768*4 = 3072
#(3)
NUM_PATCHES = (IMAGE_SIZE//PATCH_SIZE) ** 2 # (224//16)**2 = 196
#(4)
DROPOUT_RATE = 0.1
NUM_CLASSES = 10由于本文的重点是实现模型,因此我不会谈论如何训练它。但是,如果你想这样做,你需要确保你的机器上安装了GPU,因为它可以使训练更快。下面的代码块3用于检查PyTorch是否成功检测到你的Nvidia GPU。
# 代码块3
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device)
# 代码块3 output
cuda图块扁平化和线性投影实现
我之前提到过,图块扁平化和线性投影操作可以通过使用简单的MLP或卷积层来完成。在这里,我将在PatcherUnfold()和PatcherConv()类中实现它们。稍后,你可以选择在主ViT类中实现这两个类中的任何一个。
让我们先从PatcherUnfold()开始,详细信息可以在代码块4中看到。在这里,我使用了一个nn.Unfold()层。在标注有#(1)的行处可以看到,其kernel_size和步幅均为PATCH_SIZE(16)。通过这种配置,该层将对输入图像应用一个不重叠的滑动窗口。在每一步中,内部的图块都会被压平。请看下面的图4,以查看此操作的图形化展示。在该图中,我们使用大小为2的核和步幅对大小为4×4的图像应用展开操作。
# 代码块4
class PatcherUnfold(nn.Module):
def __init__(self):
super().__init__()
self.unfold = nn.Unfold(kernel_size=PATCH_SIZE, stride=PATCH_SIZE) #(1)
self.linear_projection = nn.Linear(in_features=IN_CHANNELS*PATCH_SIZE*PATCH_SIZE,
out_features=EMBED_DIM) #(2)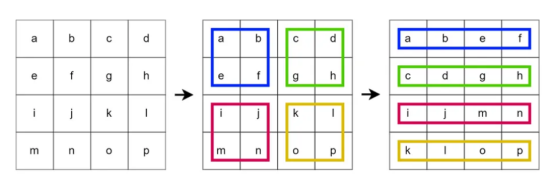
图4:在4×4图像上应用具有核大小和步幅2的展开操作
接下来,使用一个标准的nn.Linear()层(#(2))进行线性投影操作。为了使输入与扁平化的图块匹配,我们需要使用In_CHANNELS*patch_SIZE*patch_SIZE作为In_features参数,即16×16×3=768。然后,我使用设置大小为EMBED_DIM的out_features参数来确定投影结果维度(768)。值得注意的是,投影结果和扁平化的图块具有完全相同的尺寸,如ViT-B架构所规定的。如果要实现ViT-L或ViT-H,则应将投影结果维度分别更改为1024或1280,其大小可能不再与扁平化的图块相同。
因为nn.Unfold()和nn.Linear()层已经初始化,所以现在我们必须使用下面的forward()函数连接这些层。我们需要注意的一件事是,展开张量的第一和第二轴需要使用permute() 方法进行交换(#(1))。这是因为我们想将扁平的图块视为一系列标记,类似于NLP模型中处理标记的方式。我还打印出代码块中每个进程的形状,以帮助你跟踪分析数组的维度。
# 代码块5
def forward(self, x):
print(f'original\t: {x.size()}')
x = self.unfold(x)
print(f'after unfold\t: {x.size()}')
x = x.permute(0, 2, 1) #(1)
print(f'after permute\t: {x.size()}')
x = self.linear_projection(x)
print(f'after lin proj\t: {x.size()}')
return x此时,PatcherUnfold()类已经完成。为了检查它是否正常工作,我们可以尝试向它提供一个随机值的张量,该张量模拟大小为224×224的单个RGB图像。
# 代码块6
patcher_unfold = PatcherUnfold()
x = torch.randn(1, 3, 224, 224)
x = patcher_unfold(x)你可以看到下面的输出,我们的原始图像已成功转换为形状1×196×768,其中1表示单批中的图像数量,196表示序列长度(图块数量),768是嵌入维度。
# 代码块6 输出
original : torch.Size([1, 3, 224, 224])
after unfold : torch.Size([1, 768, 196])
after permute : torch.Size([1, 196, 768])
after lin proj : torch.Size([1, 196, 768])这就是使用PatcherUnfold()类实现图块扁平化展开和线性投影的过程。我们实际上也可以使用PatcherConv()实现同样的事情,代码如下所示:
# 代码块7
class PatcherConv(nn.Module):
def __init__(self):
super().__init__()
self.conv = nn.Conv2d(in_channels=IN_CHANNELS,
out_channels=EMBED_DIM,
kernel_size=PATCH_SIZE,
stride=PATCH_SIZE)
self.flatten = nn.Flatten(start_dim=2)
def forward(self, x):
print(f'original\t\t: {x.size()}')
x = self.conv(x) #(1)
print(f'after conv\t\t: {x.size()}')
x = self.flatten(x) #(2)
print(f'after flatten\t\t: {x.size()}')
x = x.permute(0, 2, 1) #(3)
print(f'after permute\t\t: {x.size()}')
return x这种方法可能看起来不像前一种方法那么简单,因为它实际上并没有使图块变扁平。相反,它使用具有EMBED_DIM(768)个内核的卷积层,从而产生具有768个通道的14×14图像(#(1))。为了获得与PatcherUnfold()相同的输出维度,我们将空间维度展平(#(2)),并交换得到张量的第一和第二轴(#(3))。为此,你可以分析下面代码块8的输出,并查看每一步后的详细的张量形状。
# 代码块8
patcher_conv = PatcherConv()
x = torch.randn(1, 3, 224, 224)
x = patcher_conv(x)
# 代码块8 output
original : torch.Size([1, 3, 224, 224])
after conv : torch.Size([1, 768, 14, 14])
after flatten : torch.Size([1, 768, 196])
after permute : torch.Size([1, 196, 768])值得注意的是,在PatcherUnfold()中使用nn.Conv2d()实现单独展开和线性投影,相比于PatcherConv()更有效,因为它将两个步骤组合成一个操作。
类标记和位置嵌入实现
在将所有图块投影到嵌入维度并排列成序列后,下一步是将类标记放在序列中的第一个图块标记之前。此过程与PosEmbedding()类中的位置嵌入实现打包在一起,如代码块9所示:
# 代码块9
class PosEmbedding(nn.Module):
def __init__(self):
super().__init__()
self.class_token = nn.Parameter(torch.randn(size=(BATCH_SIZE, 1, EMBED_DIM)),
requires_grad=True) #(1)
self.pos_embedding = nn.Parameter(torch.randn(size=(BATCH_SIZE, NUM_PATCHES+1, EMBED_DIM)),
requires_grad=True) #(2)
self.dropout = nn.Dropout(p=DROPOUT_RATE) #(3)类标记本身使用nn.Parameter()初始化。本质上,nn.Parameter()是一个权重张量(#(1))。此张量的大小需要与嵌入维度和批大小相匹配,以便它可以与现有的标记序列连接。这个张量最初包含随机值,这些值将在训练过程中更新。为了允许更新它,我们需要将requires_grad参数设置为True。同样,我们也需要使用nn.Parameter()来创建位置嵌入(#(2)),但形状不同。在这种情况下,我们将序列维度设置为比原始序列长一个标记,以容纳我们刚刚创建的类标记。不仅如此,在这里,我还使用我们之前指定的速率(#(3))初始化了一个dropout层。
之后,我将用下面代码块10中的forward()函数连接这些层。此函数接受的张量将使用torch.cat()与class_token连接,如#(1)标记的行所示。接下来,我们将在结果输出和位置嵌入张量(#(2))之间执行元素相加,然后再将其传递到dropout层(#(3))。
# 代码块10
def forward(self, x):
class_token = self.class_token
print(f'class_token dim\t\t: {class_token.size()}')
print(f'before concat\t\t: {x.size()}')
x = torch.cat([class_token, x], dim=1) #(1)
print(f'after concat\t\t: {x.size()}')
x = self.pos_embedding + x #(2)
print(f'after pos_embedding\t: {x.size()}')
x = self.dropout(x) #(3)
print(f'after dropout\t\t: {x.size()}')
return x像往常一样,让我们尝试通过这个网络向前传播一个张量,看看它是否按预期工作。请记住,pos_embedding模型的输入本质上是PatcherUnfold()或PatcherConv()产生的张量。
# 代码块11
pos_embedding = PosEmbedding()
x = pos_embedding(x)如果我们仔细看看每一步的张量维数,我们可以观察到张量x的大小最初是1×196×768。在类标记之前添加后,维度变为1×197×768。
# 代码块11输出
class_token dim : torch.Size([1, 1, 768])
before concat : torch.Size([1, 196, 768])
after concat : torch.Size([1, 197, 768])
after pos_embedding : torch.Size([1, 197, 768])
after dropout : torch.Size([1, 197, 768])转换器编码器实现
如果我们回顾一下图2,可以看到转换器编码器块由四个组件组成。我们将在下面显示的TransformerEncoder()类中定义所有这些组件。
# 代码块12
class TransformerEncoder(nn.Module):
def __init__(self):
super().__init__()
self.norm_0 = nn.LayerNorm(EMBED_DIM) #(1)
self.multihead_attention = nn.MultiheadAttention(EMBED_DIM, #(2)
num_heads=NUM_HEADS,
batch_first=True,
dropout=DROPOUT_RATE)
self.norm_1 = nn.LayerNorm(EMBED_DIM) #(3)
self.mlp = nn.Sequential( #(4)
nn.Linear(in_features=EMBED_DIM, out_features=MLP_SIZE), #(5)
nn.GELU(),
nn.Dropout(p=DROPOUT_RATE),
nn.Linear(in_features=MLP_SIZE, out_features=EMBED_DIM), #(6)
nn.Dropout(p=DROPOUT_RATE)
)标记为#(1)和#(3)的行处的两个归一化步骤是使用nn.LayerNorm()实现的。请记住,我们在这里使用的层规一化不同于我们在CNN中常见的批规一化。批归一化是通过对批中所有样本中单个特征内的值进行归一化来实现的。同时,在层归一化中,单个样本中的所有特征都将被归一化。请看下图5,以更好地说明这一概念。在这个例子中,我们假设每一行代表一个样本,而每一列都是一个特征。相同颜色的单元格表示它们的值一起归一化。
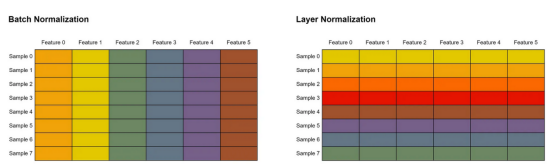
图5:批次归一化和层归一化之间差异展示(批规一化在批维度上进行规一化,而层规一化在特征维度上进行标准化)
随后,我们初始化一个nn.Multihead Attention()层,在代码块12中标记为#(2)的行处输入大小为EMBED_DIM(768)。batch_first参数设置为True,表示批处理维度位于输入张量的第0轴。一般来说,多头注意力本身允许模型同时捕捉图像块之间的各种关系。多头注意力中的每一个头都集中在这些关系的不同方面。稍后,该层接受三个输入:查询、键和值,这些都是计算所谓的注意力权重所必需的。通过这样做,这一层可以了解每个图块应该在多大程度上关注其他图块。换句话说,这种机制允许该层捕获两个或多个图块之间的关系。ViT中采用的注意力机制可以被视为整个模型的核心,因为这个组件本质上是允许ViT在图像识别任务中超越CNN性能的组件。
转换器编码器内的MLP组件是使用nn.Sequential()构造的(#(4))。在这里,我们实现了两个连续的线性层,每个层后面都有一个dropout层。我们还需要将GELU激活函数放在第一个线性层之后。第二个线性层不使用激活函数,因为它的目的只是将张量投影回原始嵌入维度。
现在,是时候使用下面的代码块连接我们刚刚初始化的所有层了。
# 代码块13
def forward(self, x):
residual = x #(1)
print(f'residual dim\t\t: {residual.size()}')
x = self.norm_0(x) #(2)
print(f'after norm\t\t: {x.size()}')
x = self.multihead_attention(x, x, x)[0] #(3)
print(f'after attention\t\t: {x.size()}')
x = x + residual #(4)
print(f'after addition\t\t: {x.size()}')
residual = x #(5)
print(f'residual dim\t\t: {residual.size()}')
x = self.norm_1(x) #(6)
print(f'after norm\t\t: {x.size()}')
x = self.mlp(x) #(7)
print(f'after mlp\t\t: {x.size()}')
x = x + residual #(8)
print(f'after addition\t\t: {x.size()}')
return x在上述forward()函数中,我们首先将输入张量x存储到残差变量(#(1))中,在该变量中,它用于创建残差连接。接下来,我们在将输入张量(#(2))输入到多头注意力层(#(3))之前对其进行归一化。正如我之前提到的,这一层将查询、键和值作为输入。在这种情况下,张量x将被用作三个参数的参数。请注意,我在代码的同一行也写了[0]。这主要是因为一个nn.MultiheadAttention()对象返回两个值:注意力输出和注意力权重;在这种情况下,我们只需要前者。接下来,在标记为#(4)的行处,我们在多头注意力层的输出和原始输入张量之间执行元素相加。然后,在执行第一次残差运算后,我们直接用当前张量x(#(5))更新残差变量。在将张量馈送到MLP块(#(7))并执行另一个元素相加操作(#(8))之前,在第#(6)行完成第二次归一化操作。
我们可以使用下面的代码块14检查我们的转换器编码器块实现是否正确。请记住,transformer_encoder模型的输入必须是PosEmbedding()产生的输出。
# 代码块14
transformer_encoder = TransformerEncoder()
x = transformer_encoder(x)
# 代码块14 output
residual dim : torch.Size([1, 197, 768])
after norm : torch.Size([1, 197, 768])
after attention : torch.Size([1, 197, 768])
after addition : torch.Size([1, 197, 768])
residual dim : torch.Size([1, 197, 768])
after norm : torch.Size([1, 197, 768])
after mlp : torch.Size([1, 197, 768])
after addition : torch.Size([1, 197, 768])从上面的输出中可以看出,每一步之后张量维度都没有变化。但是,如果你仔细看看MLP块是如何在代码块12中构造的,你会发现它的隐藏层在#(5)标记的行处扩展为MLP_SIZE(3072)。然后,我们直接将其投影回其原始尺寸,即第6行的EMBED_DIM(768)。
实现MLP头编程
我们要实现的最后一个类是MLPHead()。就像转换器编码器块内的MLP层一样,MLPHead()也包括一些全连接层、GELU激活函数和层规一化。这个类的完整的实现代码如下所示:
# 代码块15
class MLPHead(nn.Module):
def __init__(self):
super().__init__()
self.norm = nn.LayerNorm(EMBED_DIM)
self.linear_0 = nn.Linear(in_features=EMBED_DIM,
out_features=EMBED_DIM)
self.gelu = nn.GELU()
self.linear_1 = nn.Linear(in_features=EMBED_DIM,
out_features=NUM_CLASSES) #(1)
def forward(self, x):
print(f'original\t\t: {x.size()}')
x = self.norm(x)
print(f'after norm\t\t: {x.size()}')
x = self.linear_0(x)
print(f'after layer_0 mlp\t: {x.size()}')
x = self.gelu(x)
print(f'after gelu\t\t: {x.size()}')
x = self.linear_1(x)
print(f'after layer_1 mlp\t: {x.size()}')
return x在上面实现代码中,需要注意的一点是,第二个全连接层基本上是整个ViT架构的输出(#(1))。因此,我们需要确保神经元的数量与我们要训练模型的数据集中可用的种类的数量相匹配。在这种情况下,我假设我们有EMBED_DIM(10)个类。此外,值得注意的是,我最后没有使用softmax层,因为它已经在nn网络中实现了。如果你想真正训练这个模型,可以使用一下CrossEntropyLoss()。
为了测试MLPHead()模型,我们首先需要对转换器编码器块产生的张量进行切片,如代码块16中的第#(1)行所示。这是因为我们想获取符号序列中的第0个元素,它对应于我们之前在图块符号序列前面添加的类标记。
# 代码块16
x = x[:, 0] #(1)
mlp_head = MLPHead()
x = mlp_head(x)
# 代码块16 output
original : torch.Size([1, 768])
after norm : torch.Size([1, 768])
after layer_0 mlp : torch.Size([1, 768])
after gelu : torch.Size([1, 768])
after layer_1 mlp : torch.Size([1, 10])当运行上述测试代码时,我们可以看到最终的张量形状是1×10,这正是我们所期望的。
整个ViT架构
此时,所有ViT组件都已成功创建。因此,我们现在可以使用它们来构建整个视觉转换器架构了。请分析一下下面的代码块,看看我是怎么做到的。
# 代码块17
class ViT(nn.Module):
def __init__(self):
super().__init__()
#self.patcher = PatcherUnfold()
self.patcher = PatcherConv() #(1)
self.pos_embedding = PosEmbedding()
self.transformer_encoders = nn.Sequential(
*[TransformerEncoder() for _ in range(NUM_ENCODERS)] #(2)
)
self.mlp_head = MLPHead()
def forward(self, x):
x = self.patcher(x)
x = self.pos_embedding(x)
x = self.transformer_encoders(x)
x = x[:, 0] #(3)
x = self.mlp_head(x)
return x关于上述代码,我想强调几点。首先,在第1行,我们可以使用PatcherUnfold()或PatcherConv(),因为它们都有相同的作用,即执行图块展平和线性投影步骤。在这种情况下,我选用了后者。其次,转换器编码器块将重复NUM_Encoder(12)次(#(2)),因为我们将实现如图3所示的ViT-Base。最后,不要忘记对转换器编码器输出的张量进行切片,因为我们的MLP头只会处理输出的类标记部分(#(3))。
我们可以使用以下代码测试ViT模型是否正常工作。
# 代码块18
vit = ViT().to(device)
x = torch.randn(1, 3, 224, 224).to(device)
print(vit(x).size())你可以在这里看到,维度为1×3×224×224的输入已转换为1×10,这表明我们的模型按预期工作。
注意:你需要注释掉所有打印内容,使输出结果看起来更简洁一些。
# 代码块18 输出
torch.Size([1, 10])此外,我们还可以使用我们在代码开头导入的summary()函数查看网络的详细结构。你可以观察到,参数的总数约为8600万,与图3中所示的数字相匹配。
# 代码块19
summary(vit, input_size=(1,3,224,224))
# 代码块19 输出
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
ViT [1, 10] --
├─PatcherConv: 1-1 [1, 196, 768] --
│ └─Conv2d: 2-1 [1, 768, 14, 14] 590,592
│ └─Flatten: 2-2 [1, 768, 196] --
├─PosEmbedding: 1-2 [1, 197, 768] 152,064
│ └─Dropout: 2-3 [1, 197, 768] --
├─Sequential: 1-3 [1, 197, 768] --
│ └─TransformerEncoder: 2-4 [1, 197, 768] --
│ │ └─LayerNorm: 3-1 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-2 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-3 [1, 197, 768] 1,536
│ │ └─Sequential: 3-4 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-5 [1, 197, 768] --
│ │ └─LayerNorm: 3-5 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-6 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-7 [1, 197, 768] 1,536
│ │ └─Sequential: 3-8 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-6 [1, 197, 768] --
│ │ └─LayerNorm: 3-9 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-10 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-11 [1, 197, 768] 1,536
│ │ └─Sequential: 3-12 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-7 [1, 197, 768] --
│ │ └─LayerNorm: 3-13 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-14 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-15 [1, 197, 768] 1,536
│ │ └─Sequential: 3-16 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-8 [1, 197, 768] --
│ │ └─LayerNorm: 3-17 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-18 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-19 [1, 197, 768] 1,536
│ │ └─Sequential: 3-20 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-9 [1, 197, 768] --
│ │ └─LayerNorm: 3-21 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-22 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-23 [1, 197, 768] 1,536
│ │ └─Sequential: 3-24 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-10 [1, 197, 768] --
│ │ └─LayerNorm: 3-25 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-26 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-27 [1, 197, 768] 1,536
│ │ └─Sequential: 3-28 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-11 [1, 197, 768] --
│ │ └─LayerNorm: 3-29 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-30 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-31 [1, 197, 768] 1,536
│ │ └─Sequential: 3-32 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-12 [1, 197, 768] --
│ │ └─LayerNorm: 3-33 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-34 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-35 [1, 197, 768] 1,536
│ │ └─Sequential: 3-36 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-13 [1, 197, 768] --
│ │ └─LayerNorm: 3-37 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-38 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-39 [1, 197, 768] 1,536
│ │ └─Sequential: 3-40 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-14 [1, 197, 768] --
│ │ └─LayerNorm: 3-41 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-42 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-43 [1, 197, 768] 1,536
│ │ └─Sequential: 3-44 [1, 197, 768] 4,722,432
│ └─TransformerEncoder: 2-15 [1, 197, 768] --
│ │ └─LayerNorm: 3-45 [1, 197, 768] 1,536
│ │ └─MultiheadAttention: 3-46 [1, 197, 768] 2,362,368
│ │ └─LayerNorm: 3-47 [1, 197, 768] 1,536
│ │ └─Sequential: 3-48 [1, 197, 768] 4,722,432
├─MLPHead: 1-4 [1, 10] --
│ └─LayerNorm: 2-16 [1, 768] 1,536
│ └─Linear: 2-17 [1, 768] 590,592
│ └─GELU: 2-18 [1, 768] --
│ └─Linear: 2-19 [1, 10] 7,690
==========================================================================================
Total params: 86,396,938
Trainable params: 86,396,938
Non-trainable params: 0
Total mult-adds (Units.MEGABYTES): 173.06
==========================================================================================
Input size (MB): 0.60
Forward/backward pass size (MB): 102.89
Params size (MB): 231.59
Estimated Total Size (MB): 335.08
==========================================================================================总结
上面所有这些内容几乎都与视觉转换器架构有关。如果你发现代码中存在任何错误,欢迎随时发表评论。
本文中使用的所有代码也可以在我的GitHub存储库中找到。此代码的链接地址是https://github.com/MuhammadArdiPutra/medium_articles/blob/main/Paper%20Walkthrough%20-%20Vision%20Transformer%20(ViT).ipynb。
参考资料
【1】Alexey Dosovitskiy等人。《An Image is Worth 16×16 Words: Transformers for Image Recognition at Scale》(一张图顶16×16个单词:用于大规模图像识别的转换器)。Arxiv,https://arxiv.org/pdf/2010.11929。
【2】林浩宁等。《Maritime Semantic Labeling of Optical Remote Sensing Images with Multi-Scale Fully Convolutional Network》(基于多尺度全卷积网络的光学遥感图像海洋语义标注)。Research Gate,https://www.researchgate.net/publication/316950618_Maritime_Semantic_Labeling_of_Optical_Remote_Sensing_Images_with_Multi-Scale_Fully_Convolutional_Network。
【3】《Vision Transformer. PyTorch》(基于PyTorch框架的视觉转换器实现)。
Https://pytorch.org/vision/main/models/vision_transformer.html。
译者介绍
朱先忠,51CTO社区编辑,51CTO专家博客、讲师,潍坊一所高校计算机教师,自由编程界老兵一枚。
原文标题:Paper Walkthrough: Vision Transformer (ViT),作者:Muhammad Ardi



























