图像作为一种直观普遍的数据类型被广泛应用于各种任务场景中。图像既可以表示自然界中物体,也可以表示建筑、机械部件等人造几何物体。然而对于几何物体来说,使用多边形表示比图像既节省空间又更加精确。
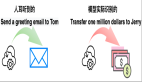
多边形表示几何物体的例子
- 地图上的建筑物:想象在二维地图上有一座矩形房屋,当作为图像表示时,这幢房屋可能需要占用数百个像素,然而只有边框的黑线才是有用的信息。多边形表示只需记录四个角的坐标和它们的连接顺序,就能准确描绘出房屋的形状。
- 雪花分形图案:当我们放大观察分形深层结构时,分形边缘会变得模糊。而多边形表示则可以轻松记录任意多的坐标点来展示深层的分形细节。
这些例子说明了,使用多边形表示几何物体比图像更有优势,特别是在需要精确性和数据效率的场景中。
多边形表征学习捕捉和编码输入多边形几何体的基本特征。这些学习到的嵌入(embeddings)对于各种下游应用具有直接的实用价值,包括城市规划、形状编码、建筑模式识别以及地理问题解答等。
与早期只关注单一多边形的研究不同,本文强调了多多边形(multipolygon)的重要性,这对于全面理解物理环境至关重要。
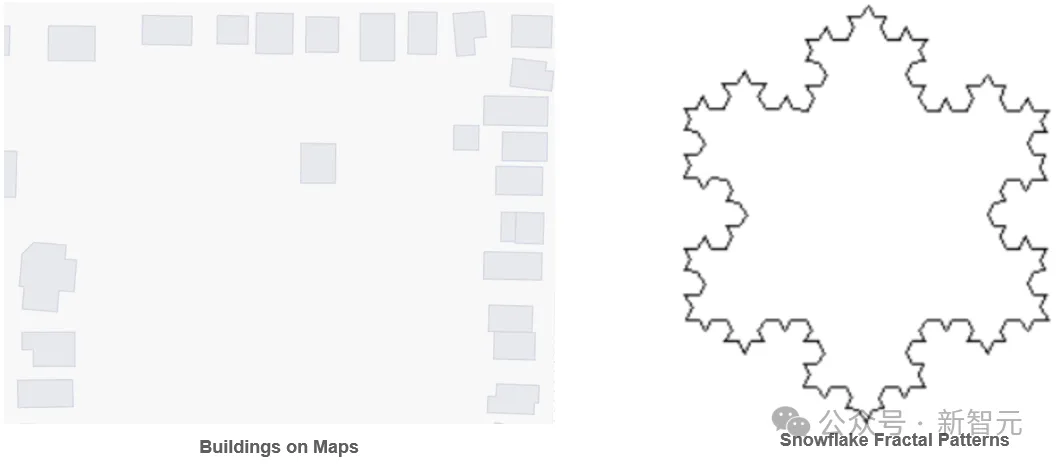
多边形应用的例子
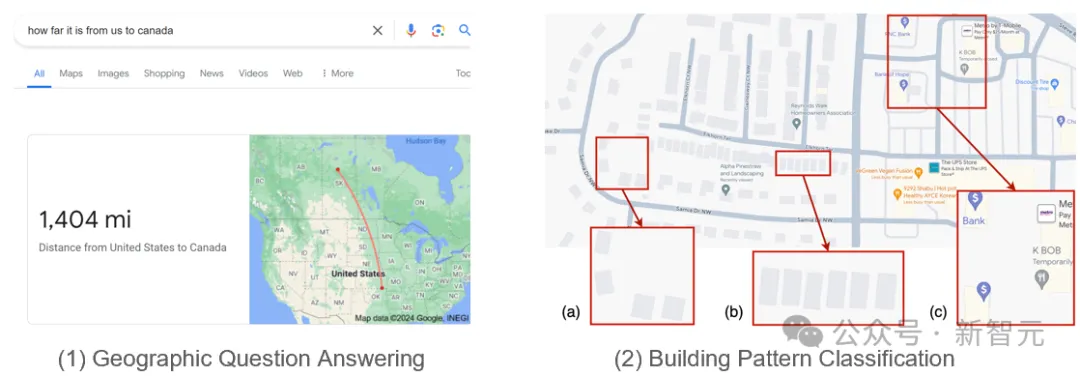
- 地理问题解答:例如,问题“加拿大到美国有多远?”需要正确编码两个多边形(美国和加拿大的地图轮廓)的关系,否则就会得到错误答案,比如“1404英里”。为了获得正确答案(0,因为两个国家接壤),我们需要对多多边形进行合理的表征学习。
- 建筑模式分析:建筑群的形状和空间分布揭示了其功能的许多信息。美国别墅区建筑通常呈现出不规则的形状,并且沿着道路松散地分布。这种随机对齐与联排别墅区形成鲜明对比,后者以统一的形状和大小紧密排列,以优化土地使用;而商业建筑则根据业务需求呈现出各种不同的形状和大小。
这些例子凸显了多多边形表征学习的重要性,不仅需要考虑单一多边形的形状,还需要考虑多个多边形之间的相互关系,以确保有效的学习。
多边形表征学习对于多个应用领域至关重要,包括形状编码、建筑模式分类和地理问题解答等。
尽管近年来该领域取得了显著进展,但大多数研究仍集中在单一多边形上,忽视了多边形间的相互关系。为了解决这一问题,埃默里大学的研究人员提出了一个用于学习通用多边形(包括单一多边形和多多边形)几何体的框架。

原文链接:https://arxiv.org/abs/2407.00742
代码链接:https://github.com/dyu62/PolyGNN
本文提出使用异质可见图(Heterogeneous Visibility Graph)表示多边形,这种图无缝整合了多边形内和多边形间的关系。为了提高计算效率并减少冗余,本文提出了一种异质生成树(Spanning Tree)抽样方法。
此外,本文设计了一种旋转-平移不变的几何表示,确保了在各种场景下的广泛适用性。
最后,本文引入了Multipolygon-GNN,一个新颖的GNN模型,来学习可见图中的空间和语义异质性。
在五个数据集上的实验表明,该模型能够有效捕捉多边形几何体的有用表征。
挑战与解决方案
开发一个能够有效学习多边形表征的机器学习模型面临诸多挑战。
1)设计一种能够保存几何细节的数据结构,这种结构需要处理多边形内关系(单个多边形的形状细节)和多边形间关系(不同多边形之间的空间动态)。这要求我们提出一种方法,将详细信息与宏观空间背景统一起来,确保没有几何信息的丢失。
为了解决这一问题,我们提出了一种可逆的多边形到异质可见图的转换过程。在这种方法中,图通过顶点和边巧妙地表示多边形的形状,同时可见性连接捕捉了多边形之间的空间关系。
2)多边形间的复杂成对关系引入了二次复杂度,这进一步要求学习方法的高效性。
为了减少异质可见图中的冗余并提高训练效率,我们开发了一种异质生成树采样策略,该策略选择性地采样可见边,实现线性复杂度。
3)多边形表征学习的一个关键是所得到表征的泛化能力。为了保持多边形几何信息的旋转和位移不变性,我们提出了一种异质几何表示,用于异质可见图中的节点。这种异质几何表示被证明能够封装图中存在的完整空间和语义信息。
4)多多边形本质上包含了层次结构,这一点虽然关键但尚未得到充分探讨。例如,一排排联排别墅可能共同构成一个更大的社区结构。识别和有效建模这些层次关系对于全面理解多边形至关重要。因此,需要先进的模型来刻画这些层次组织的模式。为此,我们开发了Multipolygon-GNN,这是一种新的图神经网络模型,通过堆叠多个层的信息传递操作,能够在不同粒度下聚合多边形模式。
方法简介
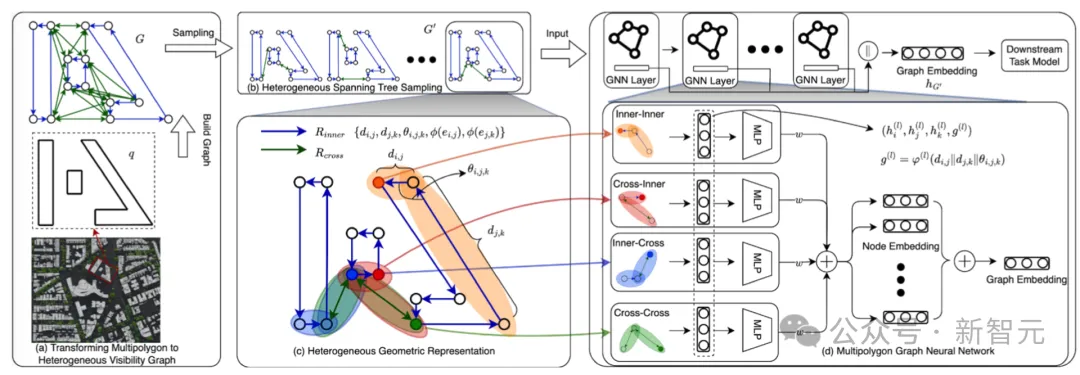
在多边形表征学习中,我们面临的一个关键挑战是如何有效地统一多边形内和多边形间的关系。为了解决这一问题,我们将多边形转换为异质可见图,如图a所示。这一过程被证明是可逆的,能够在将多边形转换为结构化数据格式的同时,保持其必要的信息。
在图b中,为了减少可见图中的冗余并解决可扩展性问题,我们提出了一种采样方法,从中抽取出简洁的图。这种方法可以有效地减少计算负担,同时保留关键的几何信息。
图c展示了我们为每个两跳路径设计的五元组异质几何表示。该表示将几何信息转换为向量形式,同时保持可见图中的信息,实现了旋转和位移不变性。通过这种表示,我们进一步消除了异质可见图中的冗余。
最后,如图d所示,我们提出了多层异质两跳信息传递机制,以刻画多边形的层次模式。这一机制能够分层学习节点的上下文信息,而不会丢失几何信息和属性。我们证明了这种异质图神经网络能够区分不同的输入图形,体现了其强大的区分能力。
异质可见图:捕捉多多边形几何及空间关系
多多边形不仅由其构成部分的形状来定义,还包括这些组成部分之间的空间关系。为了统一多多边形的这两个方面,我们提出了异质可见图的概念,G(V,E,X,ϕ)。
在我们的模型中,每个图节点表示一个多边形的顶点,其坐标作为节点特征,而形状信息由边记录。异质可见图包含了两种不同类型的边:内部边和可见边,分别用于定义个体部分的形状和连接各个部分,建模它们的空间关系。
对于可见边,我们遍历节点集𝑉,在彼此可见的节点对之间构建边。通过这种异质可见图,我们不仅捕捉了多边形的几何形状,还建模了其部分之间的空间关系,从而提供了对多边形网络的整体理解。
异质生成树采样:减少异质可见图中的冗余
我们通过利用异质可见图的特征,开发了一种线性复杂度的采样策略。关键在于理解可见边的作用,它们用于连接多多边形的各个部分。
为了确保不同部分之间的信息交换有效,需保持至少一条路径连接不同的部分。这个需求可以通过求解生成树问题来有效处理。
我们通过随机采样可见边来构建一个生成树。通过这种方法,我们有效地减少了异质可见图中的冗余,同时保持了多边形部分之间的连接性,确保了信息的完整性和有效的空间关系建模。
五元组异质几何表示:实现多边形表示的旋转和平移不变性
在多边形的表征学习中,旋转和平移不变性是一个重要目标,因为多边形结构在这些变换下保持不变,而原始坐标本身并不具备这一特性。
为了实现这一目标,我们提出了一种五元组异质几何表示。考虑所有汇聚到节点𝑣的两跳路径的集合。异质可见图G(V,E,X,ϕ)可以表示为一组元组,其中每个元组包含以下信息:节点vi与vj之间的距离,节点vj和vk之间的距离,三个节点形成的角度,构成路径的两条边的类型。
这种表示方法具有旋转和平移不变性,确保了图的结构完整性不受其方向或位置的影响。我们进一步确认,这种元组格式能够封装图的所有异质空间信息。
Multipolygon-GNN:实现层次化多边形表征学习的图神经网络
我们提出了Multipolygon-GNN来学习异质可见图中的不同交互关系。在每一层中,我们采用两跳信息传递机制,利用前述的五元组异质几何表示来更新节点嵌入。一条两跳路径可以通过不同边类型连接同一多边形部分内的节点或不同部分之间的节点。
信息从一个多边形部分流向另一个部分在学习多个多边形间的相互关系时至关重要,而内部部分的信息流则增强了对单个多边形内的局部上下文的理解。我们根据涉及的边类型将可能的路径类型划分为四类。
为了有效利用图的异质性并区分不同的信息源,我们提出了一种异质函数,根据路径类型使用不同的权重网络学习信息。我们对所有节点的嵌入进行求和,形成图嵌入。接着,将所有层的图嵌入连接起来用于下游任务。
实验验证
数据集
- MNIST-P-2:包含 10,000 个两位数多边形样本。类别:90类(数字 10-99)。
- Building-S:包含 5,000 个单建筑物多边形样本,建筑物多边形来自OpenStreetMap (OSM) 建筑数据集。建筑物的标签反映了其形状,分为十种字母形状(H, I, E, Y, T, F, U, L, Z, O)。类别:10类
- Building-2-R:包含 3,469 个双建筑物多边形样本,每个样本对为OSM建筑数据集的建筑物与其在地图上最近的邻居配对得来。类别:100类
- Building-2-C:包含 5,000 个双建筑物多边形样本。每个样本对为OSM建筑数据集的建筑物进行归一化后随即匹配而来。类别:100类
- DBSR-cplx46K:包含 46,567 个复杂多边形几何样本,每个样本由两个多边形组成,分类判断两个多边形是否有包含关系。类别:2类有效性分析
表格展示了五个数据集上的性能比较。特别是在 MNIST-P-2 数据集上,PolygonGNN在准确率、精确率、F1 分数和 AUC 指标上均取得了最高分,显著超越了其他方法。在 Building-2-C和Building-2-R数据集中,尽管绝对性能一般,但PolygonGNN依然显著优于其他方法。
这两个数据集由于是直接从地图中抽取的,每个建筑的方向并未校准对齐,可能出现颠倒的状况导致标签本身存在争议。
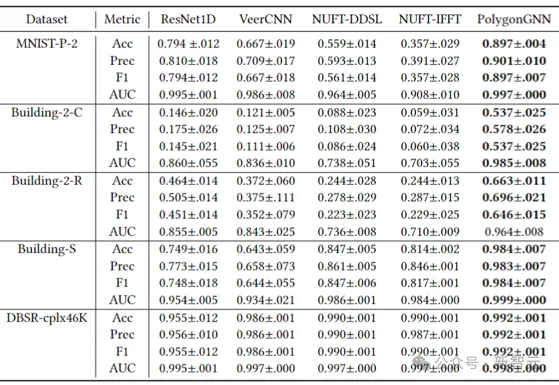
Building-S作为单个建筑物的数据集不存在标签争议,DBSR-cplx46K数据集数据量很大并且任务相对简单,因此所有方法在这两个数据集上都取得了较好的表现。
以上实验说明PolygonGNN在单一多边形和多多边形数据上都优于现有方法,尤其是在多多边形数据上具有绝对优势。本文其他实验可以参考原文。
总结 & 限制性
本文提出了PolygonGNN,一个强大的多边形表征学习框架。PolygonGNN通过用异质可见图统一了单一多边形和多多边形的表征学习,在多种多边形数据集上达到了最先进的性能。
局限性:PolygonGNN在采样可见边的时候选择仅保留一条可见边连接不同的部分,这可能会限制信息在不同部分之间的传递。未来的研究可以设计自适应采样策略根据不同部分的复杂性动态调整可见边数量,或者将输入图进行多级粗化(coarsening),利用分层图神经网络(Hierarchical GNN)分步学习每个部分的表征和全局表征,同时考虑不同部分之间的相对空间信息。