4月30日,KAN横空出世,很多人预言这会敲响MLP的丧钟。
没想到,子弹还没飞4个月,核心团队又推出了KAN 2.0,瞄准AI+Science领域,进一步挖掘了KAN的潜力。

这篇论文更雄心勃勃的地方在于,作者希望通过一种框架来弥合AI世界的连接主义(connectionism)和科学世界的符号主义(symbolism)之间的不相容性。
通过提出pykan等工具,作者还展现了KAN发现各种物理定律的能力,包括守恒量、拉格朗日量、隐藏对称性和本构方程等等。

论文地址:https://arxiv.org/abs/2408.10205
这次KAN 2.0依旧出自初代架构原班人马之手。

深度学习变天了,MLP成过去式?
我们先简要回顾一下,今年4月首次提出的KAN究竟在哪些方面改进了MLP。
MLP(multi-layer perceptron)又被称为全连接神经网络,是当今几乎所有深度学习模型的基础构建块,它的出世甚至可以追溯到第一波人工智能浪潮方兴未艾的1958年。

论文地址:https://www.ling.upenn.edu/courses/cogs501/Rosenblatt1958.pdf
KAN的论文中都表示,MLP的重要性怎么强调都不为过,因为这是神经网络中用于逼近非线性函数的默认模型,其对函数表达能力的底层逻辑由「通用逼近定理」保证。
Transformer和其他架构中常见的FFN本质上就是一个MLP。但由于网络稠密、参数量大,MLP往往占据了模型中几乎所有的非编码层参数。
而且相比注意力层,在没有后期分析工具时,MLP中的大量参数也缺乏可解释性。
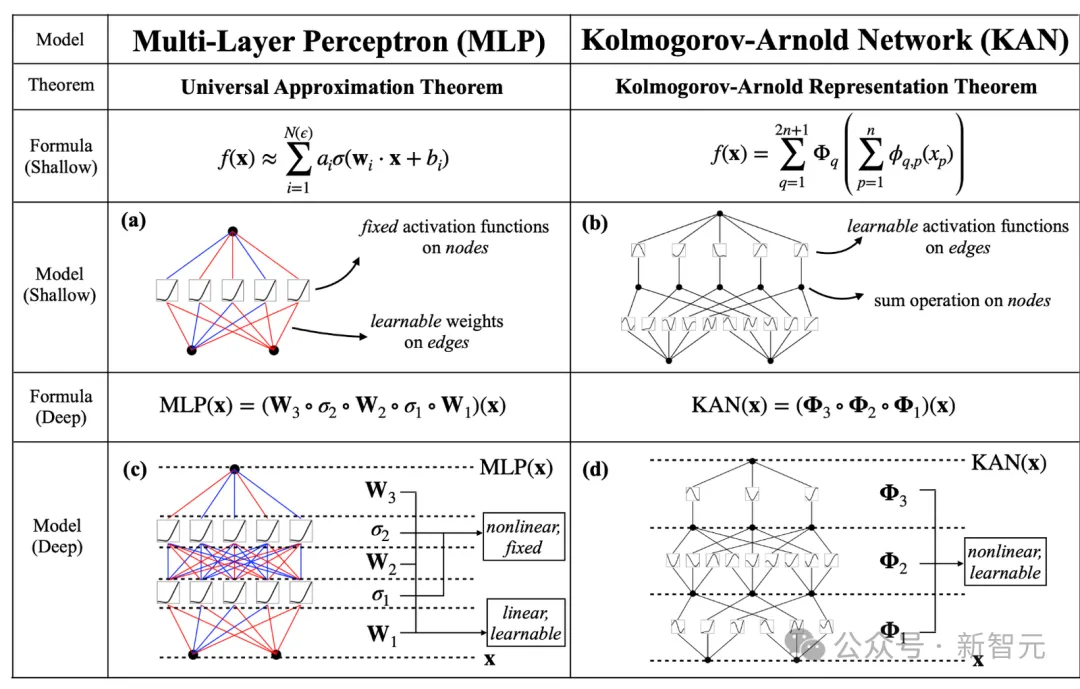
受到Kolmogorov-Arnold表示定理的启发,KAN打破了对通用逼近定理的遵循。
虽然底层逻辑变了,但是他们做出的修改相当简洁且直观:
- 将激活函数放在网络边缘而非节点处
- 给激活函数赋予可学习参数,而非固定的函数
KAN中没有任何线性权重,网络中的每个权重都变成了B-spline型单变量函数的可学习参数。
这种看似简单的改变让KAN获得了拟合准确性和可解释性方面的优势。今年4月的第一篇论文中,作者们就发现KAN在数学和物理定律方面的潜力。
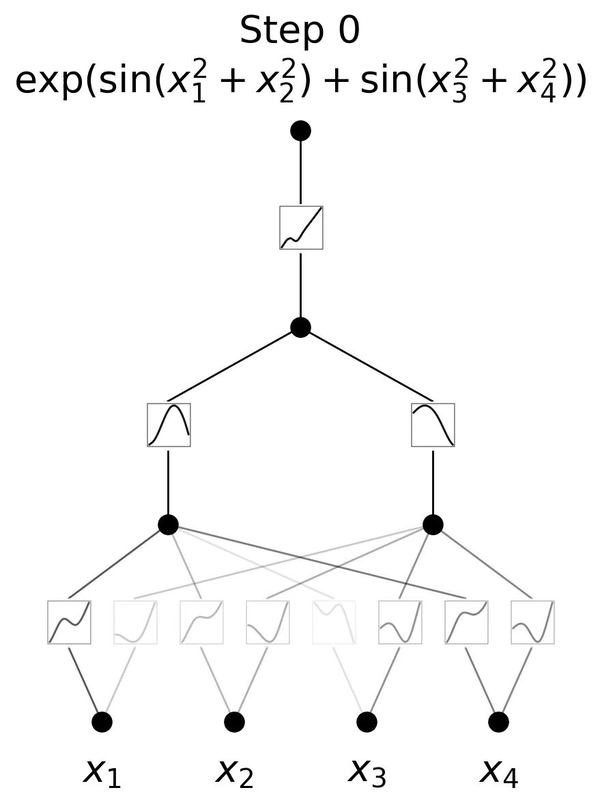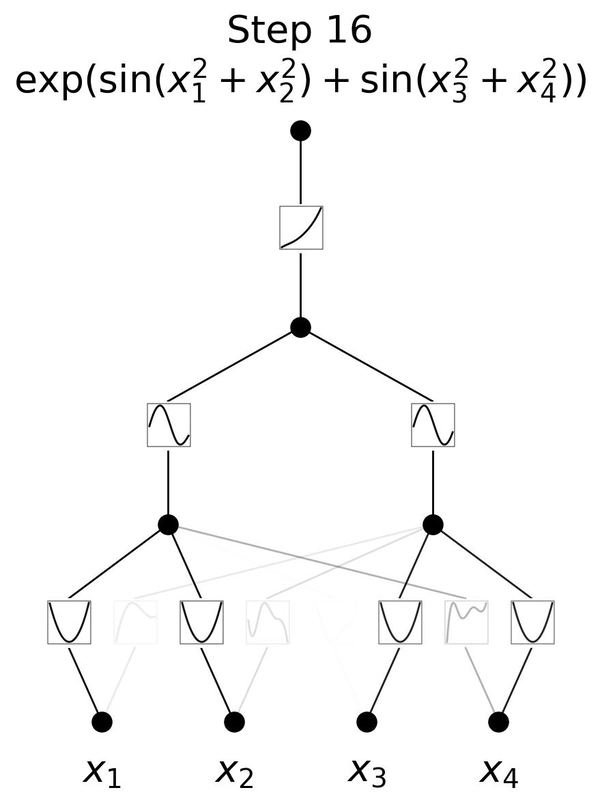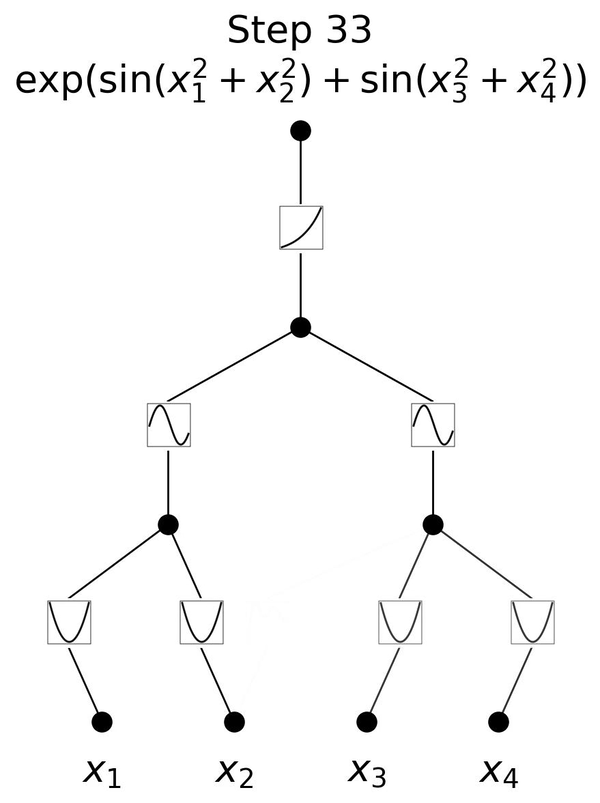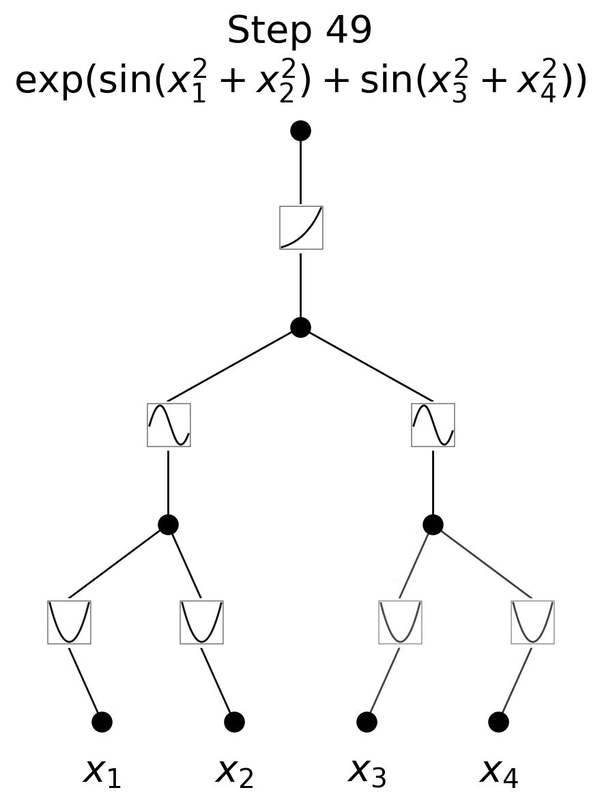
下面这个动图展示了简单的3层KAN网络拟合一个复杂函数的训练过程,相当简洁清楚。
此外,KAN也能从根本上很好地解决MLP中普遍存在的「灾难性遗忘」问题。
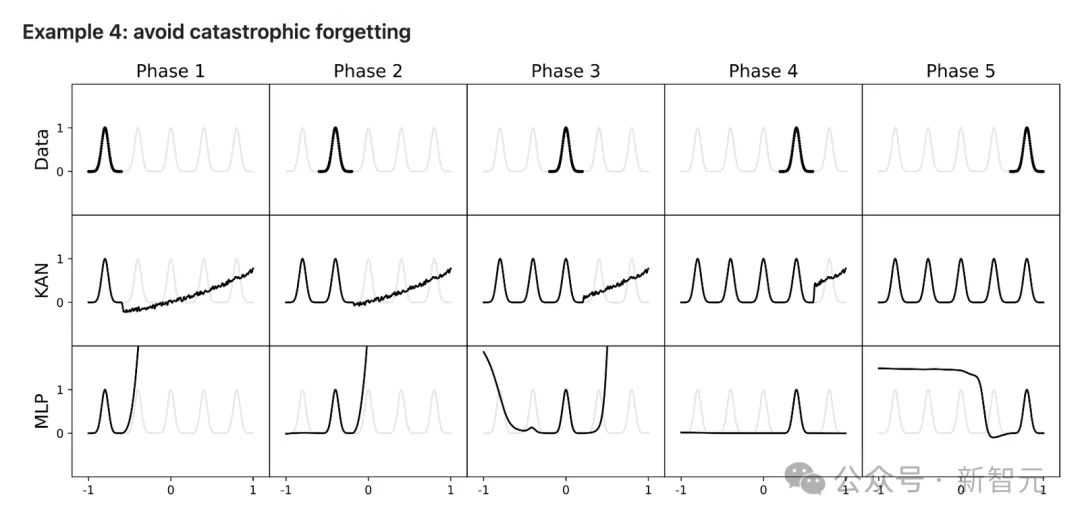
以上这些优势,都奠定了KAN作为「科学家合作助手」的基本能力。
KAN2.0问世,一统AI+科学
虽然第一版的KAN网络本身有很多适合科学研究的优点,但深度学习和物理、化学、生物学领域依旧有完全不同的「语言」,这构成了AI4Science最大的障碍之一。
因此扩展后的KAN 2.0的终极目标只有一个——使KAN能轻松应用于「好奇心驱动的科学」。研究人员既能将辅助变量、模块化结构、符号公式等科学知识集成到KAN中,也能从KAN的可解释性分析中得到观察和见解。

所谓「好奇心驱动的科学」,根据论文的解释,是过程更具有探索性、提供更基础层面新发现和新知识的研究,比如天体运动背后的物理原理,而非AlphaFold这类应用驱动的科学研究。
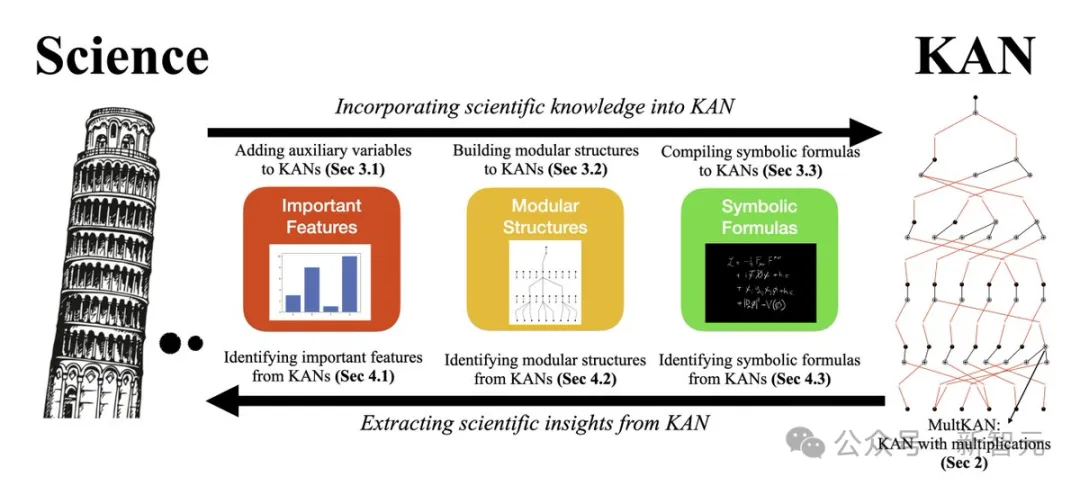
科学与KAN的协同
具体来说,科学解释有不同的层次,从最简单粗略到最精细、最难发现、最具因果性,可以有如下几个分类:
- 重要特征:例如,y完全由x1和x2决定,其他因素并不重要;即存在一个函数f使得y=f(x1, x2)
- 模块化结构:例如,存在函数g和h是的y=g(x1)+h(x2)
- 符号公式:例如,y=sin(x1)+exp(x2)
MultKAN
在原始KAN网络的基础上,这篇最新的论文引入了一种称为MultKAN的新模型,其核心改进是引入额外的乘法层进行增强。
KAN所依据的Kolmogorov-Arnold表示定理提出,任何连续高维函数都可以分解为单变量连续函数和加法的有限组合:
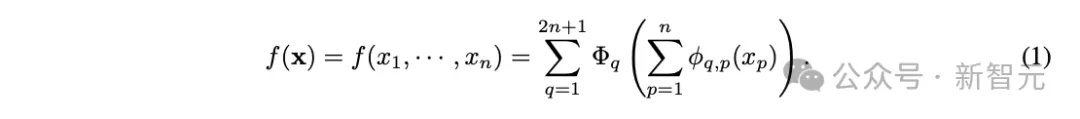
这意味着加法是唯一真正的多元运算,,而其他多元运算(包括乘法)都可以表示为与单变量函数组合的加法。因此,原来的KAN中仅包含加法运算。
然而,考虑到乘法在科学和日常生活中的普遍存在,MultKAN中明确包含乘法,能更清楚地揭示数据中的乘法结构,以期增强可解释性和表达能力。
如图2所示,MultKAN和KAN相似,都包含标准KAN层,但区别在于插入了乘法节点,对输入的子节点进行乘法运算后再进行恒等变换,用Python代码可表示为:
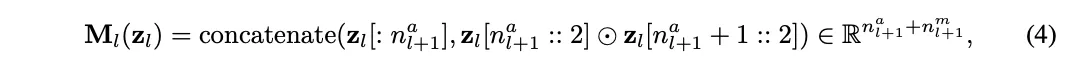
其中⊙表示逐元素乘法。
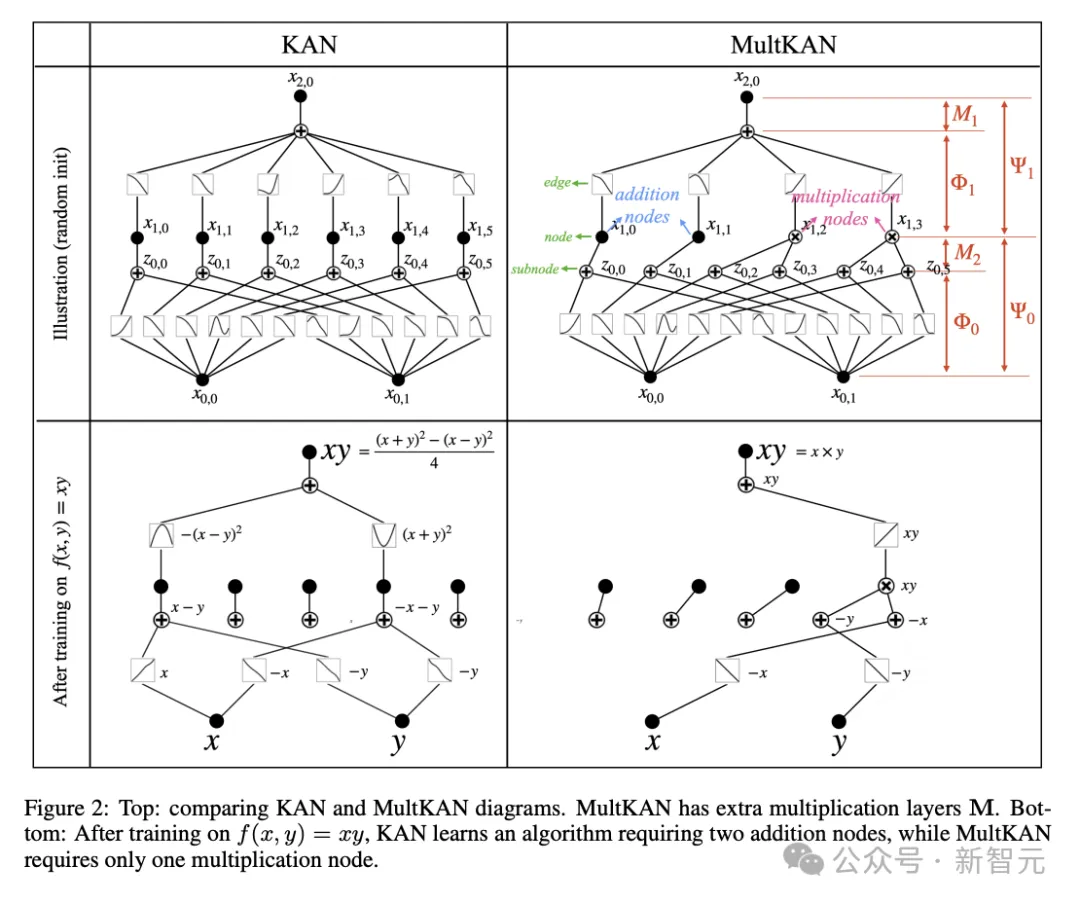
根据上图,整个MultKAN网络进行的运算就可以写作:
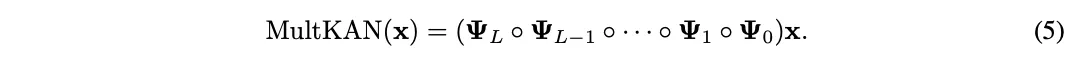
其中,𝚿L≡𝐌L∘𝚽L。
经过扩展后,论文将KAN和MultKAN视为同义词,即默认情况下的KAN都将允许乘法层的存在,除非有特殊说明。
GitHub仓库中的KAN代码已经更新,可以通过pip快捷命令直接安装使用。

仓库地址:https://github.com/KindXiaoming/pykan
Science to KAN
在科学领域,领域知识至关重要,让我们可以在数据稀少或不存在的情况下,也能有效工作。
因此,对KAN采用基于物理的方法会很有帮助:将可用的归纳偏置整合到KAN中,同时保持其从数据中发现新物理规律的灵活性。
文中作者探讨了三种可以整合到KAN中的归纳偏置,从最粗略(最简单/相关性)到最精细(最困难/因果关系):重要特征、模块化结构和符号公式。
在KANs中添加重要特征
在回归问题中,目标是找到一个函数f,使得y=f(x1, x2, ···, xn)。假设我们希望引入一个辅助输入变量a=a(x1, x2, ..., xn),将函数转化为y=f(x1, ···, xn, xa)。
尽管辅助变量a不增加新的信息,但它可以提高神经网络的表达能力。这是因为网络无需消耗资源来计算辅助变量。此外,计算可能变得更简单,从而提升可解释性。
这里,用户可以使用augment_input方法向输入添加辅助特征:
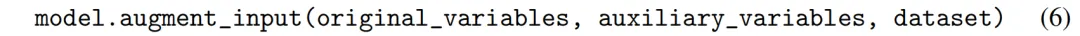
图3显示了包含辅助变量和不包含这些辅助变量的KAN:(a)由符号公式编译而成的KAN,需要5条连接边;(b)(c)包含辅助变量的KAN,仅需2或3条连接边,损失分别为10⁻⁶和10⁻⁴。
为KAN构建模块化结构
模块化在自然界中非常普遍:比如,人类大脑皮层被划分为几个功能不同的模块,每个模块负责特定任务,如感知或决策。模块化简化了对神经网络的理解,因为它允许我们整体解释神经元群集,而不是单独分析每个神经元。
结构模块化的特点是连接群集,其中特征是群集内的连接远强于群集间的连接。为此,作者引入了module方法:保留群集内的连接,同时去除群集间的连接。
模块由用户来指定,语法是:

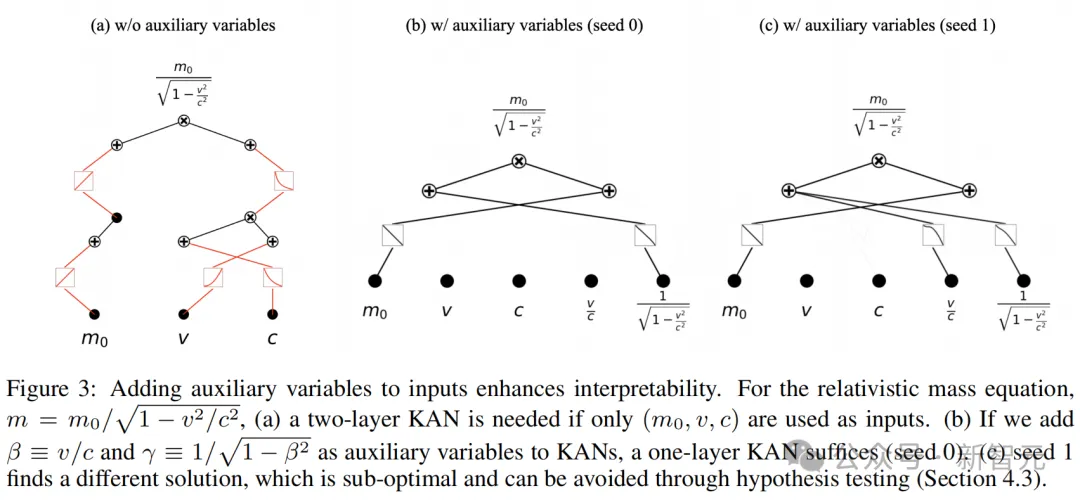
具体而言,模块化有两种类型:可分性和对称性。
可分性:如果说一个函数是可分的,那么它就可以表示为非重叠变量组的函数的和或积。
广义对称性:如果f(x1, x2, x3, ···)=g(h(x1, x2), x3, ···),则这个函数在变量(x1, x2)上是对称的。因为只要h(x1, x2)保持不变,即使x1和x2发生变化,f的值仍然保持不变。
将符号公式编译成KAN
为了结合「符号方程」和「神经网络」这两种方法的优势,作者提出了一个两步程序:(1)将符号方程编译成KAN,(2)使用数据微调这些KAN。
其中,第一步可以将已知的领域知识嵌入到KAN中,而第二步则专注于从数据中学习新的「物理」知识。
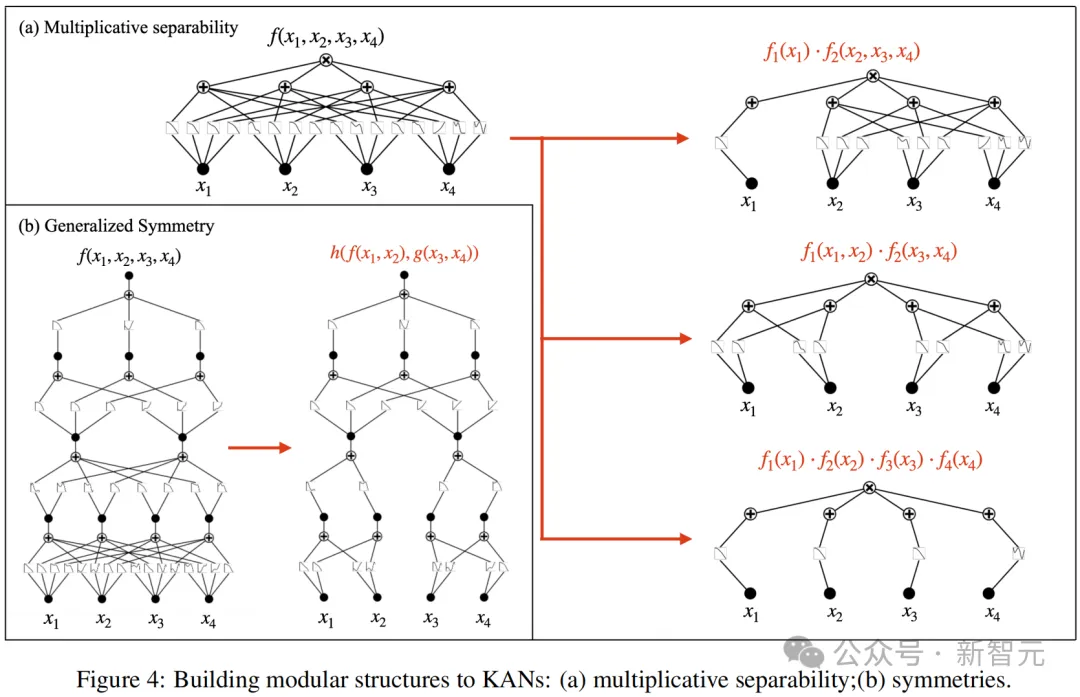
具体来说,作者首先提出了用于将符号公式编译成KAN的kanpiler(KAN编译器)。过程如图5a所示:
1. 将符号公式解析为树结构,其中节点表示表达式,边表示操作/函数;
2. 然后修改该树以与KAN图结构对齐。修改包括通过虚拟边将所有叶节点移动到输入层,并添加虚拟子节点/节点以匹配KAN架构。这些虚拟边/节点/子节点仅执行恒等变换;
3. 在第一层中组合变量,有效地将树转换为图。

然而,通过宽度/深度扩展来增加表达能力kanpiler生成的KAN网络是紧凑的,没有冗余边,这可能限制其表达能力并阻碍进一步的微调。
为了解决这个问题,作者又提出了expand_width和expand_depth方法来扩展网络,使其变得更宽和更深,如图5c所示。
KAN to Science
这一节同样关注提取知识的三个层次,从最基本到最复杂:重要特征,模块化结构和符号公式。
识别重要特征
给定一个回归模型f,有y≈f(x1,x2,…,xn) ,我们的目标是为输入变量分配重要性分数。
论文提出,之前所使用的L1范数(图6a)只考虑到了局部信息,因此得出的结果可能存在问题。
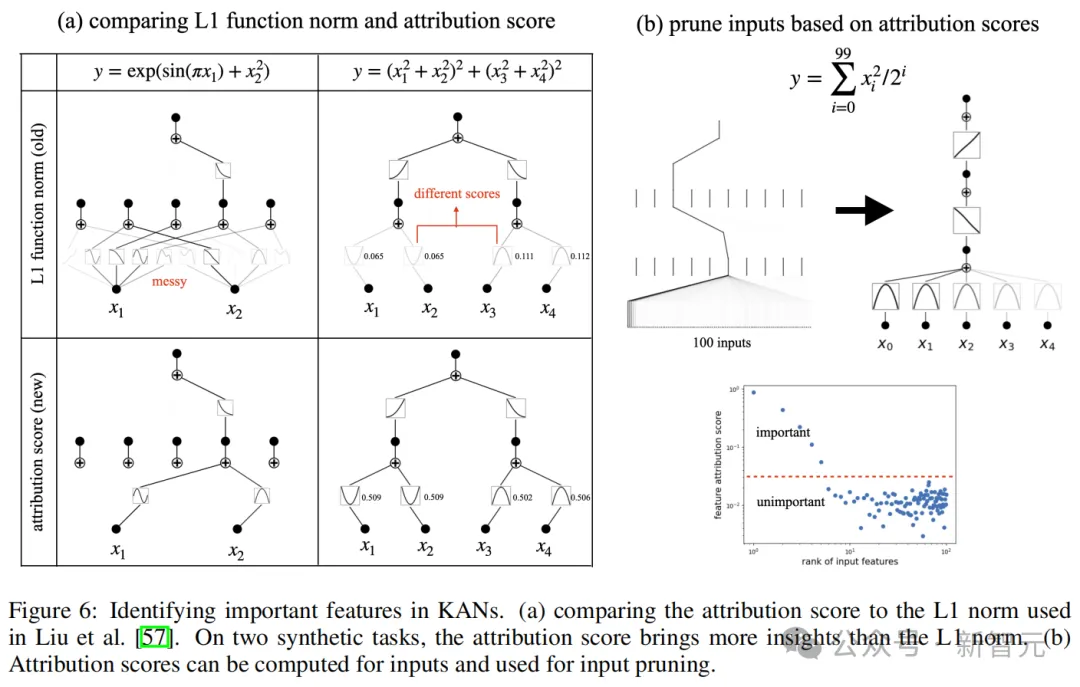
依据KAN网络,作者提出了一种更有效的归因分数,能比L1范数更好反映变量的重要性,还可以根据这种归因分数对网络进行剪枝。
识别模块化结构
归因分数可以告诉我们哪些边或节点更有价值,但它没有揭示模块化结构,即重要的边和节点如何连接。
神经网络中的模块化结构可以分为两种:解剖模块化(anatomical modularity)和功能模块化(functional modularity)。
解剖模块化是指,空间上彼此靠近的神经元相比距离较远的神经元具有更强的连接趋势。论文采用了之前研究提出的「神经元交换」方法,在代码中被称为auto_swap,可以在保留网络功能的同时缩短连接,有助于识别模块。
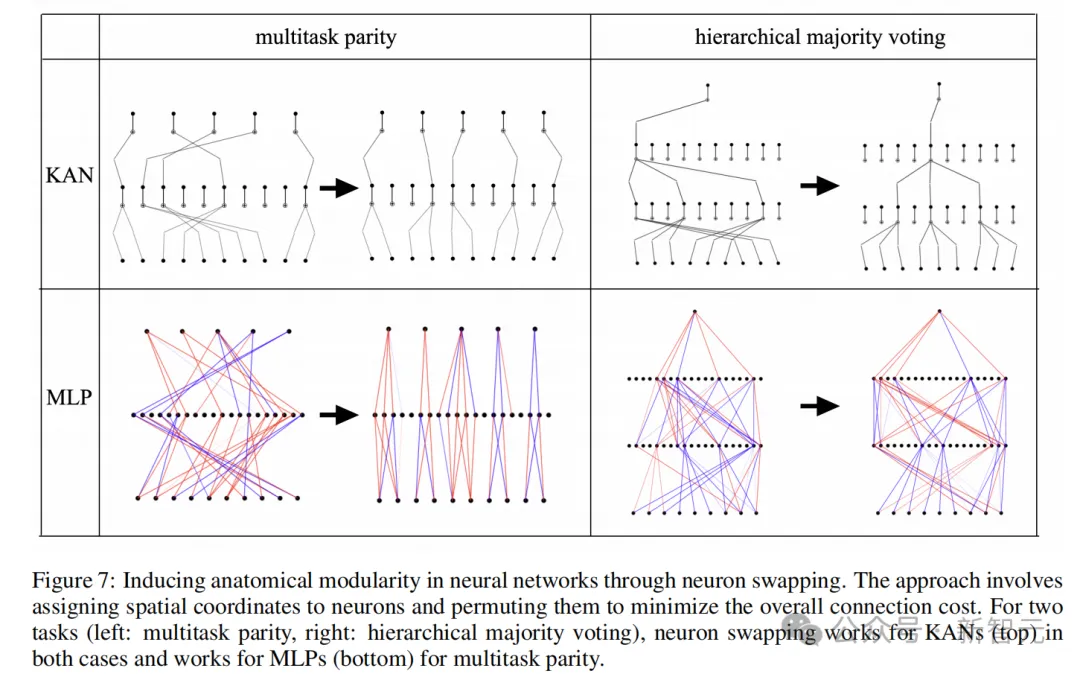
图7展示了两个成功识别模块的auto_swap任务:多任务匹配和分层多数投票。其中,KAN的模块结构相比MLP更加简单且富有组织性。
但无论auto_swap结构如何,网络全局的模块化结构仍和整体功能仍不清楚,这就需要用到功能模块化分析,通过输入和输出的前向和后向传递来收集有关信息。
图8定义了三种类型的功能模块化:可分性、一般可分性和一般对称性。
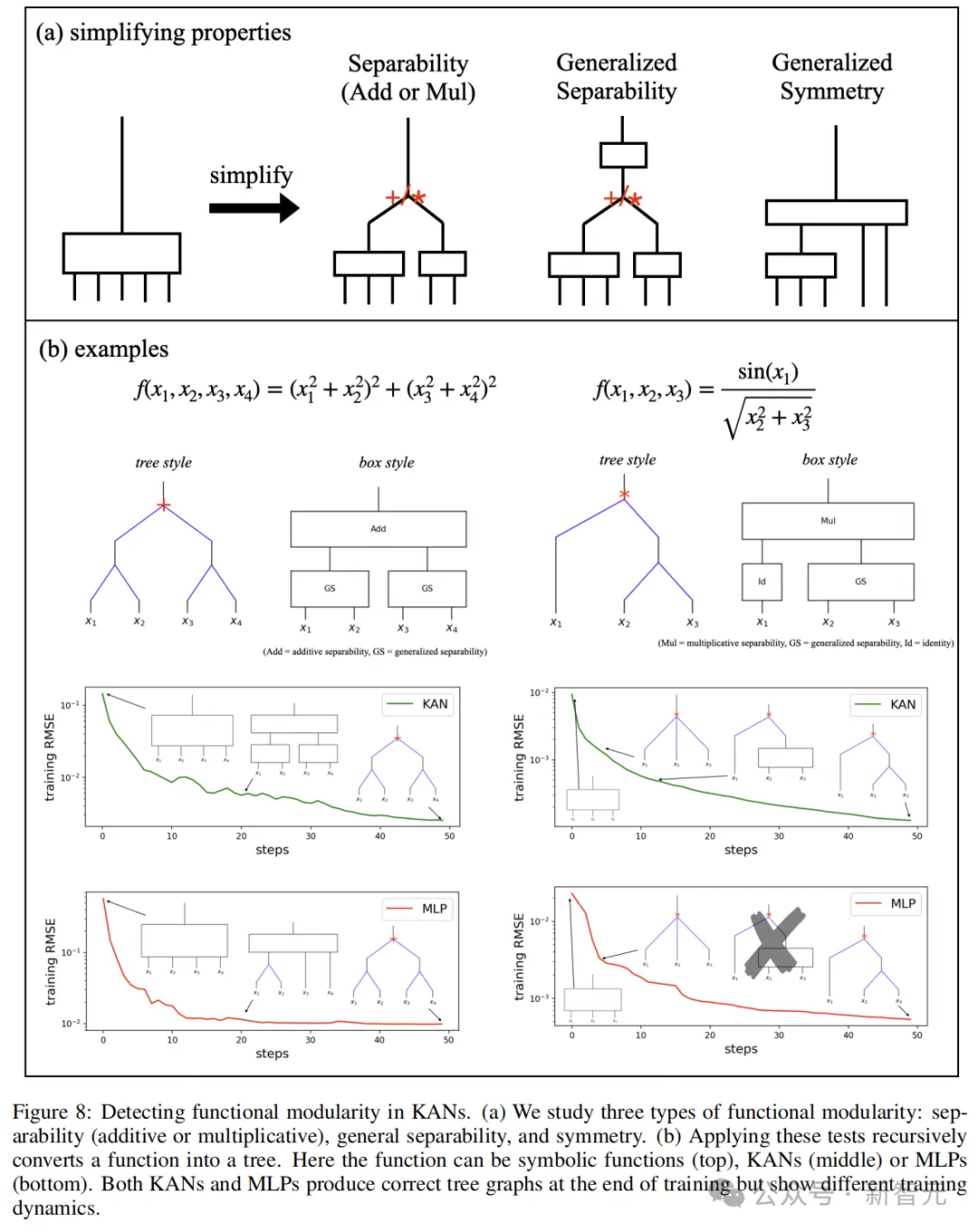
识别符号公式
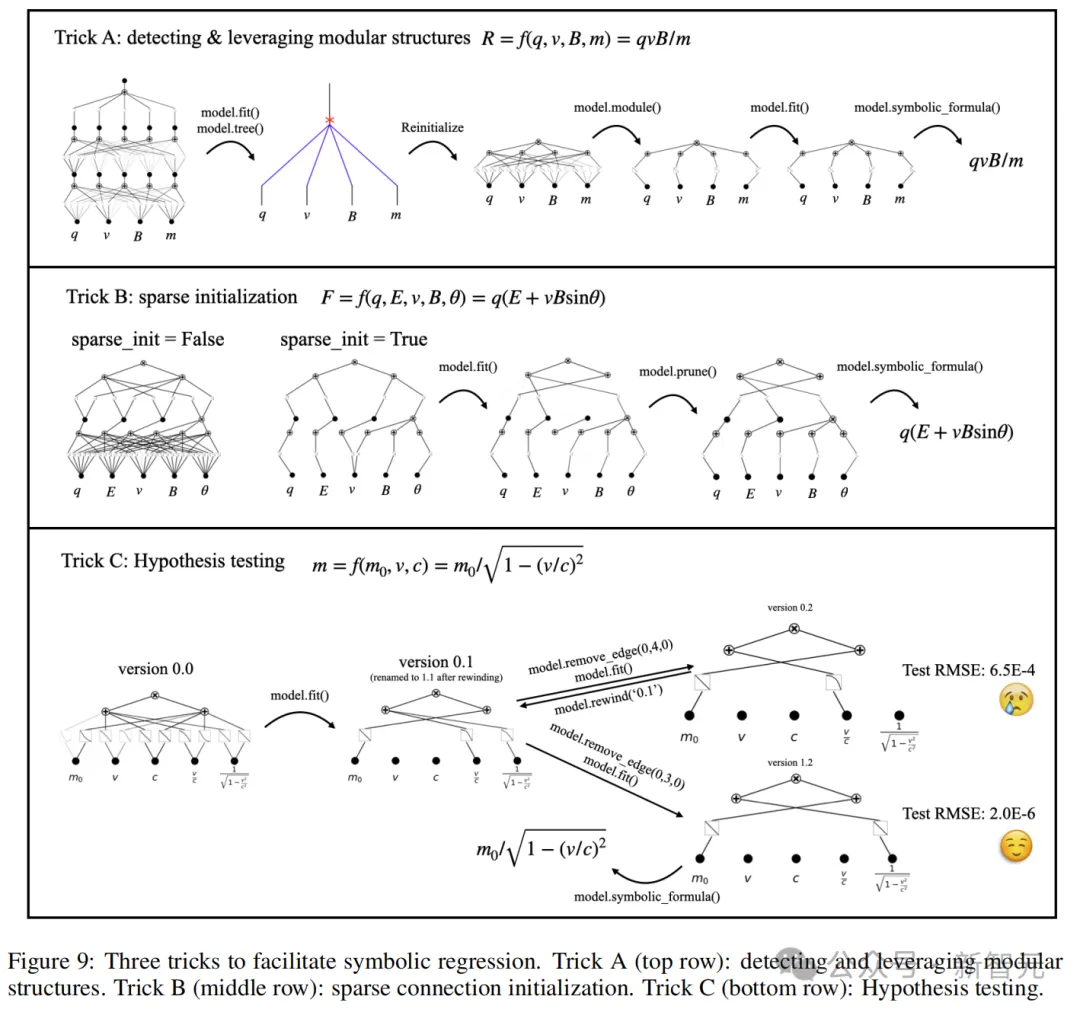
符号公式信息量最大,因为可以直接、清楚地揭示函数中重要的特征和模块结构。图9展示了与KAN进行交互协作进行符号回归的3个技巧:
1.发现并利用模块化结构
2.稀疏初始化
3.假设检验
用KAN助力物理学研究
除了进行原理层面的说明,论文还讲解了多个具体案例,如何将KAN融入到现实的科学研究中,比如发现新的物理概念和定律。
论文给出的案例包括守恒量、拉格朗日量、隐藏对称性和本构方程等。这里我们以最简单的守恒量发现为例,看看KAN是如何工作的。
守恒量即时间变化过程中保持恒定的物理量,比如能量守恒定律告诉我们,孤立系统的总能量保持不变。
传统上,科学家如果不借助计算工具,仅靠纸笔推导守恒量可能非常耗时,并且需要广泛的领域知识。但机器学习方法可以将守恒量参数化,转化为求解微分方程的问题。
此处所用的方法基本类似于作者Ziming Liu等人2022年发表的论文,但将其中的MLP网络换成了KAN。

论文地址:https://pubmed.ncbi.nlm.nih.gov/36397460/
比如使用KAN可以发现二维谐振子(x, y, px, py)中具有3个守恒量:x轴方向的能量H1、y轴方向的能量H2和角动量H3。
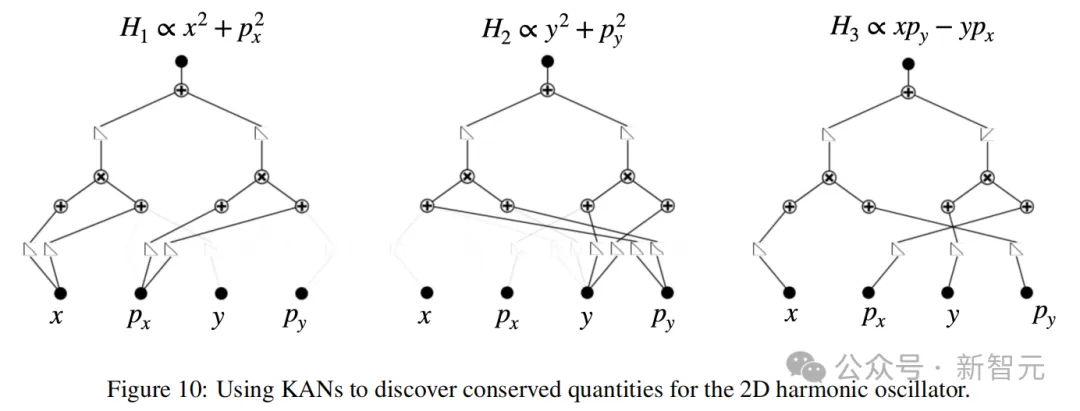
关于KAN的其他应用,论文也描述了如何从实验数据中推断出拉格朗日量(图11)。
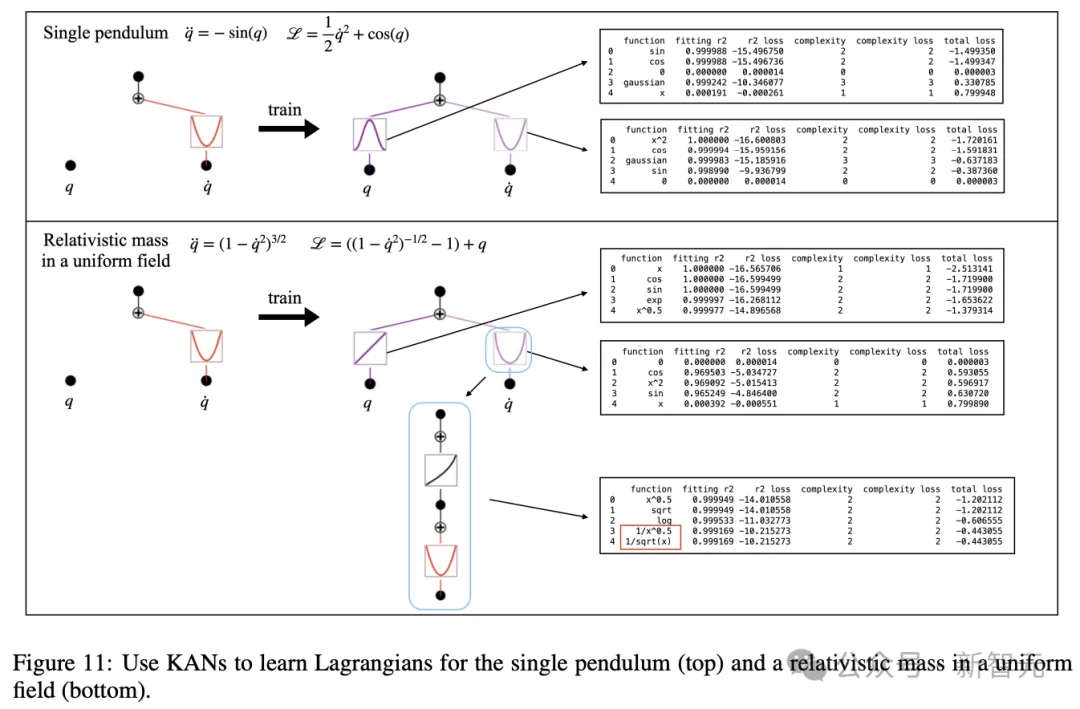
或者,发现Schwarzschild黑洞中的隐藏对称性(图12)。
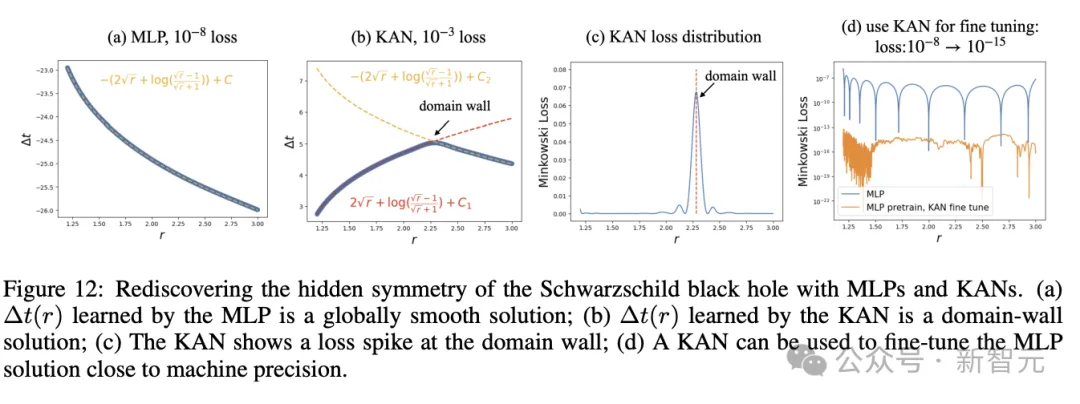
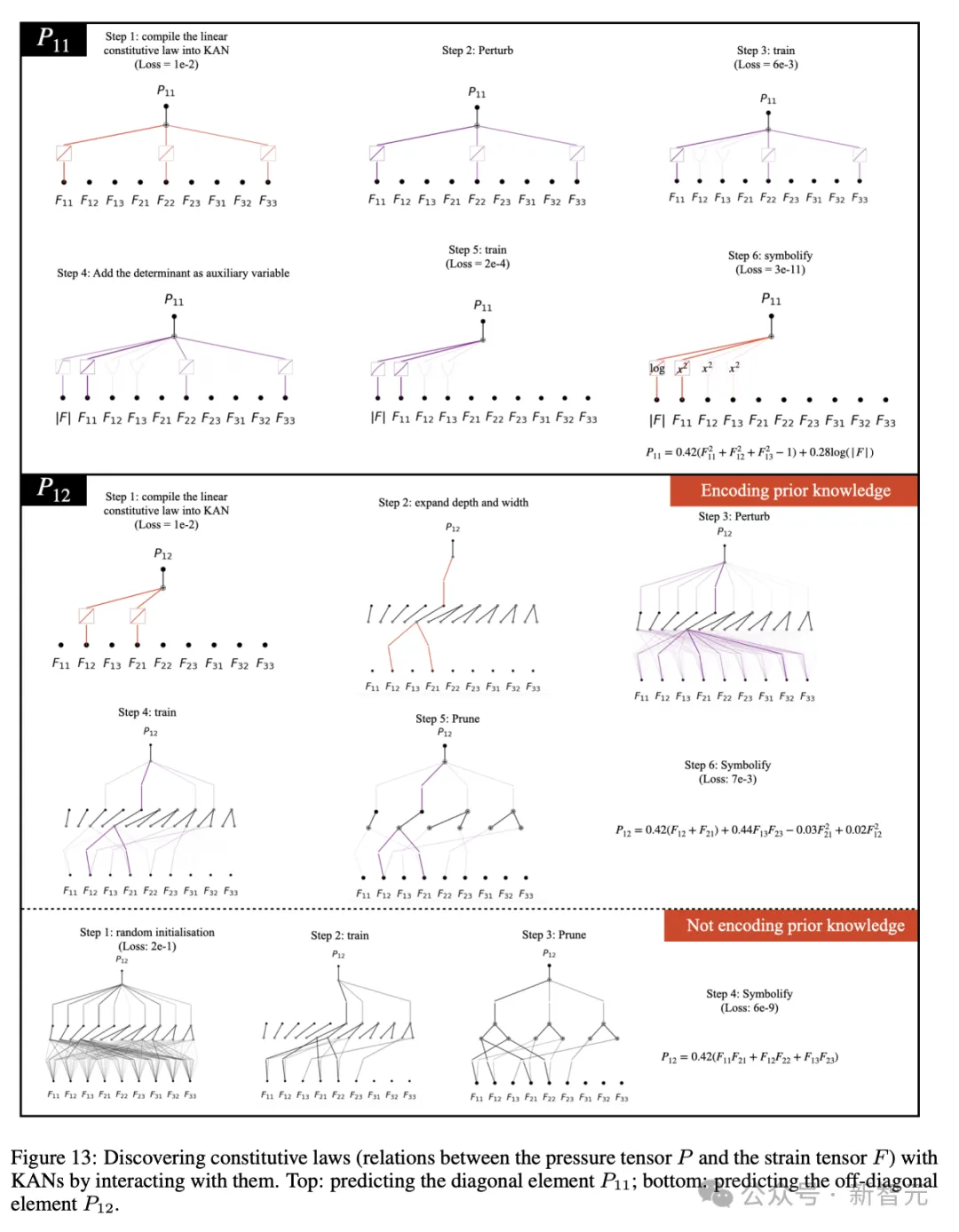
还有数据驱动的本构定律发现(图13)。本构定律通过模拟材料对外力或变形的响应,定义材料的行为和属性,比如描述弹簧的胡克定律。
作者介绍
Ziming Liu(刘子鸣)

Ziming Liu目前是MIT和IAIFI的三年级博士生,由Max Tegmark教授指导。他是两篇KAN论文的第一作者,可以说是这个架构背后最主要的贡献者。
他的研究兴趣主要集中在AI与物理学(以及其他科学领域)的交叉区域:
1. Physics of AI:从物理学原理来理解AI,目标是让「AI像物理学一样简单」;
2. Physics for AI:受物理学启发的AI,目标是让「AI像物理学一样自然」;
3. AI for physics:利用AI增强物理学研究,目标是让「让AI像物理学家一样强大」。
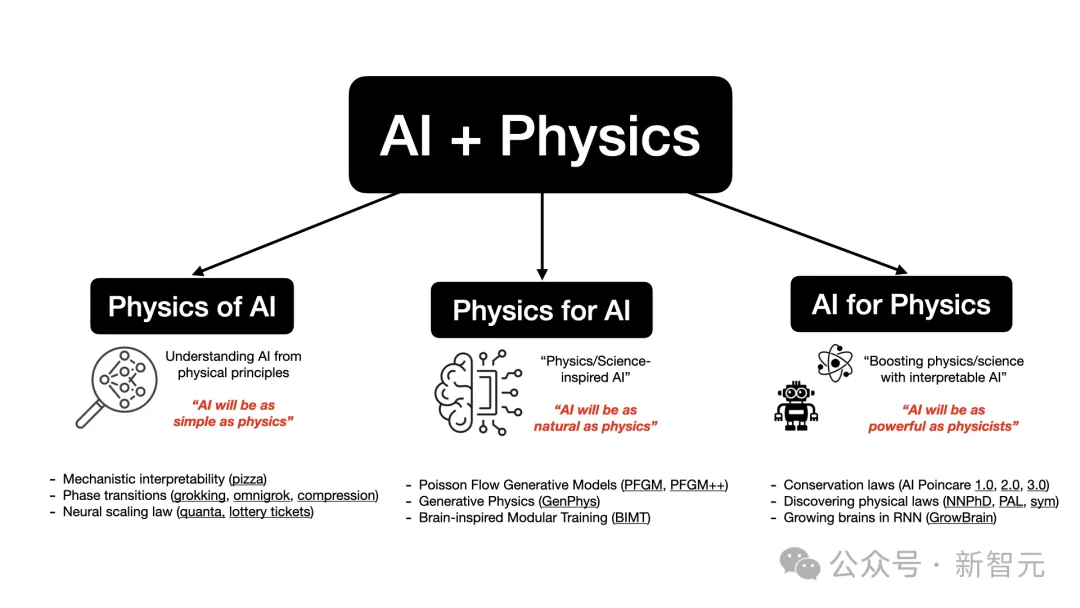
为了实现利用AI和物理学共建更美好世界的最终目标,Ziming Liu对包括发现物理定律、受物理启发的生成模型、机器学习理论、机械解释性等在内的多个主题都有深厚的兴趣。
并且,与凝聚态、高能物理、量子计算等领域的物理学家以及计算机科学家、生物学家、神经科学家和气候科学家等建立了紧密合作关系。
他多次在顶尖的物理期刊和AI会议上发表论文,并担任IEEE、Physical Review、NeurIPS、ICLR等的审稿人。同时,还共同组织了NeurIPS 2021和ICML 2022的AI4Science workshop。
在攻读博士学位之前,他在北京大学获得了物理学学士学位,并曾在微软亚洲研究院实习。

Pingchuan Ma(马平川)

Pingchuan Ma目前是MIT CSAIL实验室的博士生,由Wojciech Matusik教授指导。
他的研究方向涵盖了「基于物理的智能」的整个流程:
1. 重建高效逼真的物理环境
2. 基于这些环境生成AI 智能体
3. 在物理世界中实现这些智能体
此前,他在南开大学获得软件工程专业学士学位,并在麻省理工学院获得计算机科学硕士学位。

同时,他还在IBM、字节、商汤、港大等知名机构从事过研究工作,有着丰富的经验。
Yixuan Wang

Yixuan Wang目前是加州理工学院,应用及计算数学专业的博士生。
他的研究方向十分广泛,包括数值分析、偏微分方程、应用概率,以及AI for Science。
此前,他在北京大学获得数学学士学位。
Wojciech Matusik

Wojciech Matusik是麻省理工学院计算机科学与人工智能实验室(MIT CSAIL)的电气工程与计算机科学教授,也是计算机图形学小组的成员,负责带领计算设计与制造团队。
他的研究兴趣包括计算机图形学、计算设计与制造、计算机视觉、机器人学和人机交互。
他于2003年在MIT获得计算机图形学博士学位,2001年在MIT获得电气工程与计算机科学硕士学位,1997年在加州大学伯克利分校获得电气工程与计算机科学学士学位。

并他曾在三菱电机研究实验室、Adobe和迪士尼苏黎世研究所工作。
2004年,他被「麻省理工科技评论」评为全球100位顶尖青年创新者之一。2009年,获得了ACM Siggraph的杰出新研究者奖。2012年,获得了DARPA青年教师奖,并被评为斯隆研究学者。2014年,获得了Ruth和Joel Spira卓越教学奖。
Max Tegmark

Max Tegmark被大家亲切地称为「疯狂的麦克斯」(Mad Max)。
凭借着自己创新的思维和对冒险的热情,他的科研兴趣涵盖从精确宇宙学到探索现实的终极本质。
比如,结合理论与新的测量技术,精确限定宇宙学模型及其参数。在他作为物理学研究者的前25年里,这种研究方向使他主要关注宇宙学和量子信息学。
虽然他仍与HERA合作研究宇宙学,但目前他的主要研究方向是智能的物理学,即运用物理方法深入探索生物智能和AI。
作为麻省理工学院的物理学教授,他发表了超过两百篇技术论文,并多次在科学纪录片中出现。他在SDSS项目中关于星系聚类的研究,赢得了《科学》杂志「2003年度突破」的第一名。
在此之前,Tegmark于1989年在斯德哥尔摩经济学院获得了经济学学士学位,1990年在皇家理工学院获得物理学学士学位。
毕业后,他便前往加州大学伯克利分校继续深造,先后获得物理学硕士和博士学位。
在美国西海岸生活四年后,他回到了欧洲,出任马克斯·普朗克物理研究所的助理研究员。
1996年,他作为Hubble Fellow以及普林斯顿高级研究院的研究员,再次来到美国。
几年后,他获得宾夕法尼亚大学的助理教授职位,并于2003年获得终身教职。
2004年,他来到MIT并定居在查尔斯河畔的剑桥。





























