使用H统计量分析机器学习模型特征相关性-51CTO.COM

Friedman 的 h 统计量 (h-stat) 为复杂的机器学习模型提供了一个强大的窗口。具体来说，它可以帮助我们了解它们是否使用交互来进行预测。我们将看到，这种XAI（可解释性机器学习）方法可以告诉我们一个特征是否与任何其他特征或一个特定特征交互。为此，我们将：

使用 Python 包 artemis 应用 h-stat 。
解释输出，包括交互热图和条形图。

H-stat 是什么？

相互作用是指特征与目标变量之间的关系取决于另一个特征的值。h-stat 通过将两个或多个特征的联合部分依赖 (PD) 函数与假设特征不相互作用的联合 PD 进行比较来量化此相互作用。

重要的一点是，该指标有两个版本：

成对 h-stat — 给出一个特征通过与另一个特征的交互产生的效果的百分比
总体 h-stat — 给出某个特征与所有其他特征相互作用所产生的效果的百分比

为了能够根据特征效果的百分比来解释指标，我们对它们进行了归一化。然而，这个过程有时会夸大交互效应。这种情况可能发生在尽管特征的大部分效果来自交互，但整体效果很小的情况下。这就是为什么我们也有这两个指标的非归一化版本。当应用该方法时，我们会看到所有这些版本相互补充。

artemis 使用

要应用 H-stat，我们将使用artemis包。这是一个用于分析机器学习模型中交互的有用包。它提供了其他方法，包括 Greenwell 方法和一些特定于模型的方法。

import pandas as pd 
import matplotlib.pyplot as plt 
import random 

from sklearn.ensemble import RandomForestRegressor 
from artemis.interactions_methods.model_agnostic import FriedmanHStatisticMethod

数据和模型

我们将使用鲍鱼数据集（https://archive.ics.uci.edu/dataset/1/abalone）来了解 ALE 的工作原理。鲍鱼是一种美味的贝类。我们希望使用壳重和去壳重量（肉的重量）等特征来预测其壳中的环数。图 1显示了此数据集中所有数值特征的相关性热图。你可以看到我们正在处理一些高度相关的特征。

这是一个重要的问题。H -stat 的局限性之一是，当特征实际上高度相关时，它可以识别交互作用。这些被称为虚假交互作用。随后我们可以通过使用散点图确认 h-stat 的结果。

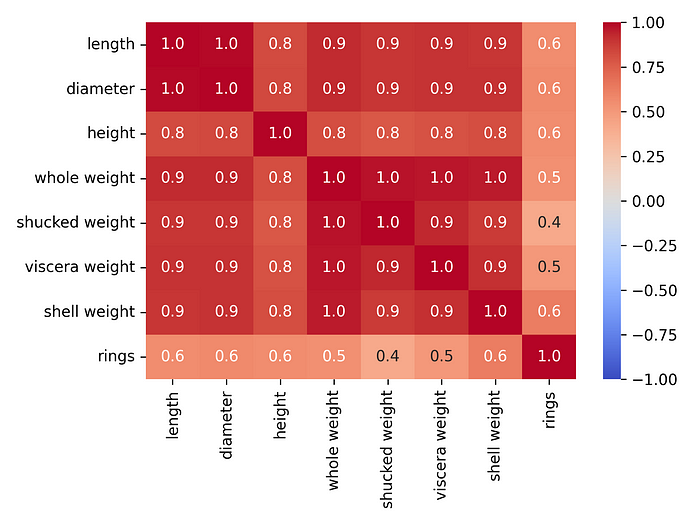图 1：鲍鱼数据集中数值特征的相关性热图

我们加载数据集并选择目标变量。我们还进行了一些特征工程。首先，我们排除一些高度相关的特征。这是因为在图 1中我们看到它们与其他特征的相关性为 1。最后，我们为性别特征创建独热编码。

#导入数据集
data = pd.read_csv("../../data/abalone.data",
                  names=["sex","length","diameter","height","whole weight",
                         "shucked weight","viscera weight","shell weight","rings"])

y = data["rings"]
X = data[["sex", "length", "height", "shucked weight", "viscera weight", "shell weight"]]

# 创建虚拟变量
X['sex.M'] = [1 if s == 'M' else 0 for s in X['sex']] 
X['sex.F'] = [1 if s == 'F' else 0 for s in X['sex']] 
X['sex.I'] = [1 if s == 'I' else 0 for s in X['sex']]
X = X.drop('sex', axis=1)

X.head()

图 2：鲍鱼数据集特征

我们使用这些特征来训练模型来预测环的数量。在本例中，我们使用了随机森林模型（h-stat 与模型无关，因此这应该能够将其应用于大多数建模包）。

# 训练模型
model = RandomForestRegressor() 
model.fit(X, y)

总体H-stat

H-stat 的计算成本很高，很多场景不太适合高维数据集。这里我们首先从特征矩阵中随机选择一组 100 个实例，以获得稳定的指标估计值。

# 随机选择 100 个观测值
random.seed(8) 
X_exp = random.choices(X.to_numpy(), k=100) 
X_exp = pd.DataFrame(X_exp, columns=X.columns)

创建一个 H-stat 对象。然后使用 100 个实例来计算模型的 H-stats。

# 计算 H 统计量
h_stat = FriedmanHStatisticMethod() 
h_stat.fit(model, X_exp)

直接将指标可视化为整体交互的图。

# 整体交互图
fig, ax = plt.subplots(figsize=(10 , 5)) 
h_stat.plot(vis_type='bar_chart_ova', ax=ax)

从该图表中，我们可以看出，壳重和去壳重量的相互作用似乎很显著（或至少比其他特征更显著）。壳重对预测环数的影响中约有35% 来自与其他特征的相互作用。对于去壳重量，该值约为27% ，而对于其他特征，该值不到10% 。

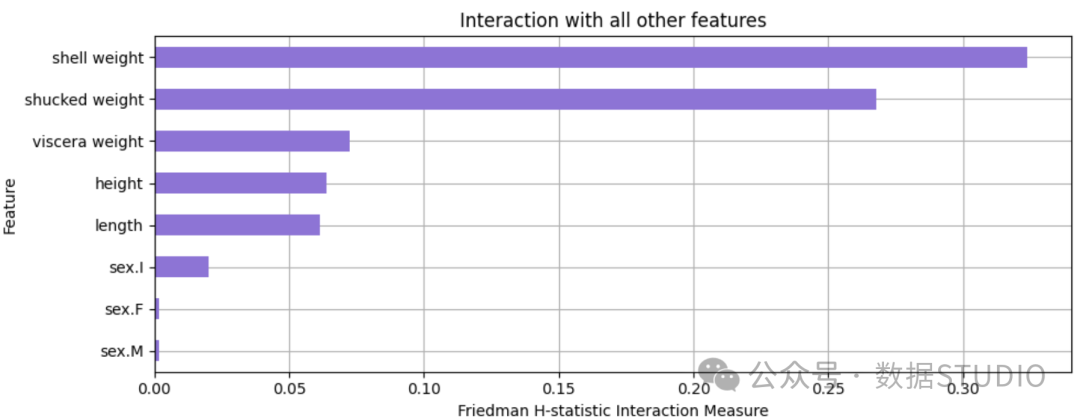图 3：H 统计量显示与所有其他特征的相互作用

成对 H-stat

问题是壳重和去壳重量与哪些特征有相互作用？。为此可以使用下面的代码绘制成对的 H-stat。

# 成对 h-stat
fig, ax = plt.subplots(figsize=( 10 , 4 )) 
h_stat.plot(vis_type='bar_chart', ax=ax)

该图表明这些特征相互作用。它们的联合 PDP 中约 24% 的变化来自两个特征之间的相互作用。长度和内脏重量（length:viscera weigh）之间的相互作用可能也不太显著。

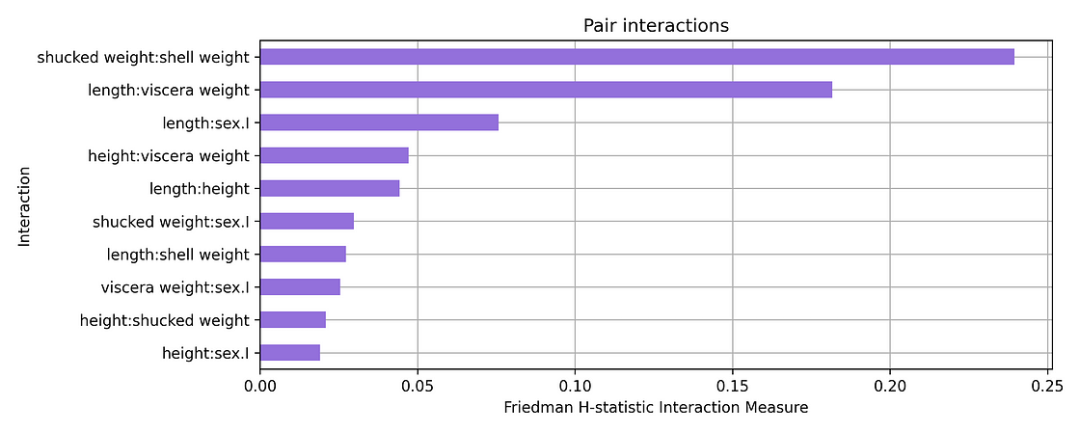图 4：显示成对相互作用的 H 统计量的条形图

更直观的可视化此信息的方法是使用热图（直接设置参数即可）。对角线给出了每个特征的排列特征重要性分数。我们可以看到，不仅这两个特征（shell weight:shucked weight）的相互作用显著，而且它们的自身作用也显著。

# 交互热图
h_stat.plot()

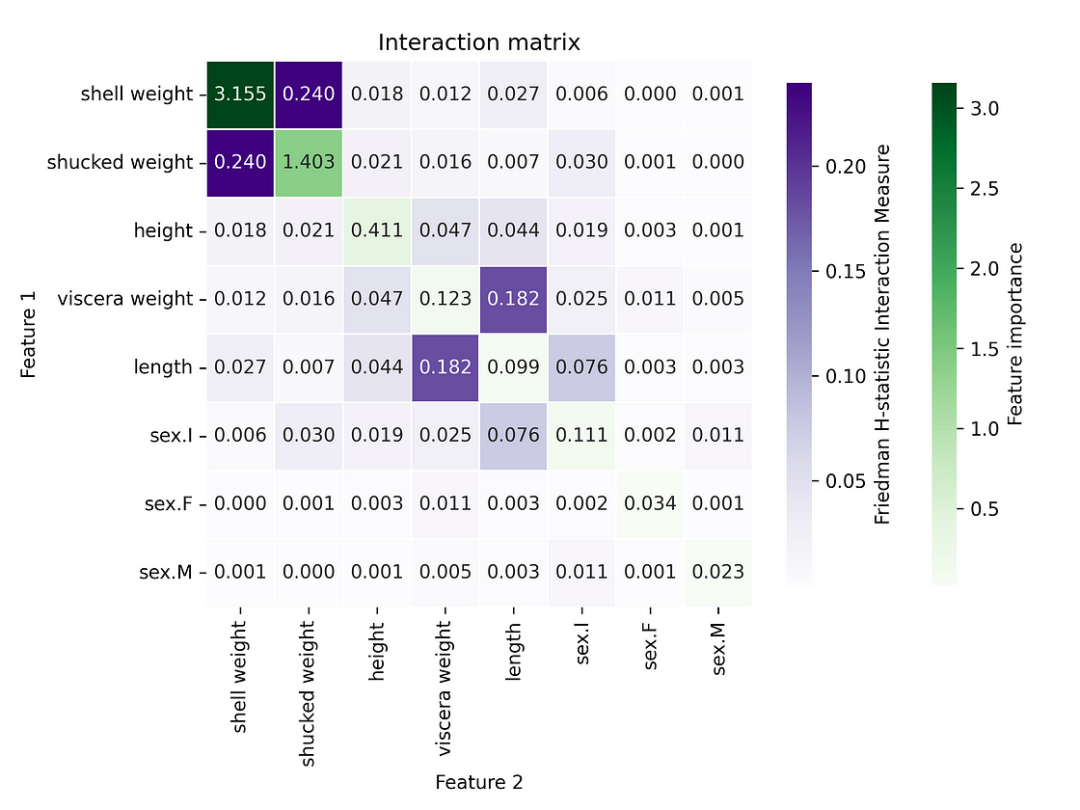图 5：H-stat 热图显示成对相互作用

非标准化H-stat

如上所述，通过标准化 H-stat，我们可以夸大一些相互作用。artimise 包可以计算未标准化的值。为此，我们使用与之前相同的代码，只是我们将 normalized 参数设置为 False。

h_stat_unnormalized = FriedmanHStatisticMethod(normalized= False ) 
h_stat_unnormalized.fit(model, X_exp) 

# 绘制热图
h_stat_unnormalized.plot()

交互值不再全部介于 0 和 1 之间。内脏重量和长度（ viscera weight: length）之间的交互似乎不再显著。所以也许它在之前的图中被夸大了。

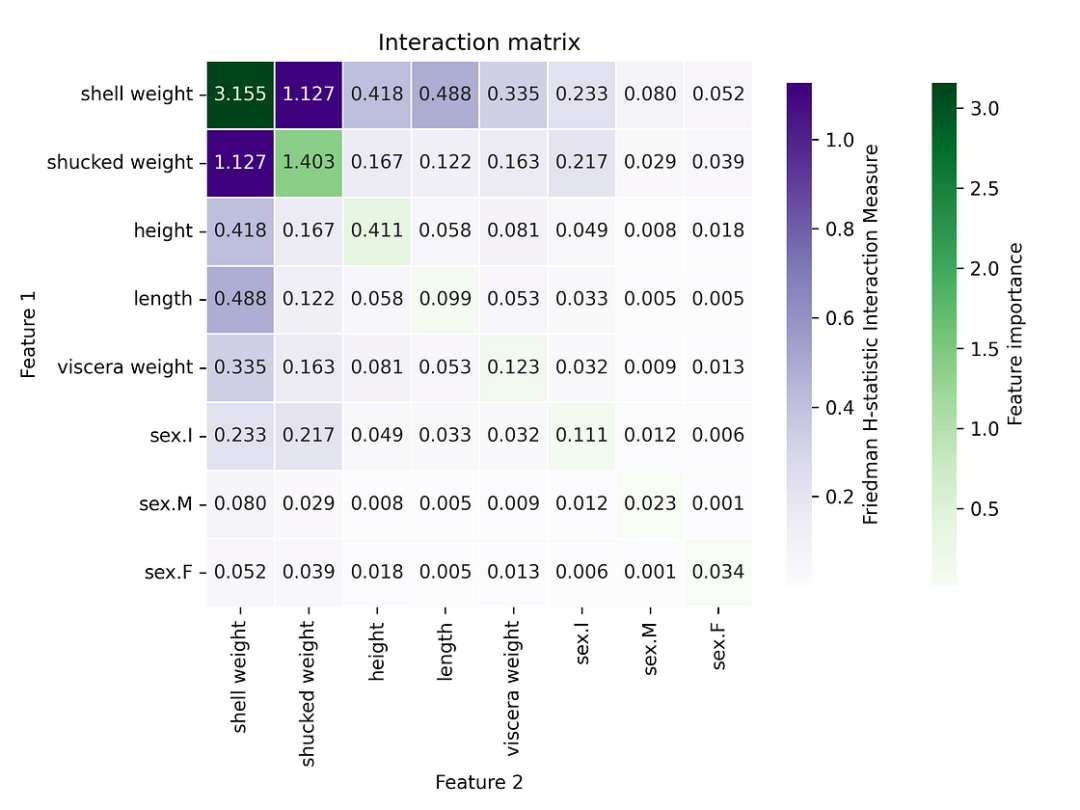图 6：H 统计量热图显示未标准化的成对相互作用

此时，我们应该考虑H-stat 的另一个弱点——虚假相互作用。在图 1中，我们看到模型特征都高度相关。因此，我们需要确保 H-stat 不会将多重共线性与相互作用混淆。

一种方法是将底层数据集中的交互可视化。为此，我们创建了壳重与去壳重的散点图。我们根据环数对点进行着色，并添加颜色条。现在可以清楚地看到这种相互作用的性质。

# 壳重量和去壳重量之间的相互作用
plt.scatter(X["shell weight"], X["shucked weight"], c=y, cmap="bwr")
plt.colorbar(label="Number of Rings", orientatinotallow="vertical")
plt.xlabel("shucked weight", size=15)
plt.ylabel("shell weight", size=15)

我们可以看到，环的数量会随着去壳重量的增加而增加。同时，当去壳重量（鲍鱼肉的重量）相对于鲍鱼壳较大时，环的数量也会更多。可能发生的情况是，鲍鱼的壳会随着年龄的增长而增长，在某个时候，它会停止增长。然而，鲍鱼肉会继续增长。这就是为什么我们看到最老的鲍鱼肉比鲍鱼壳更多。

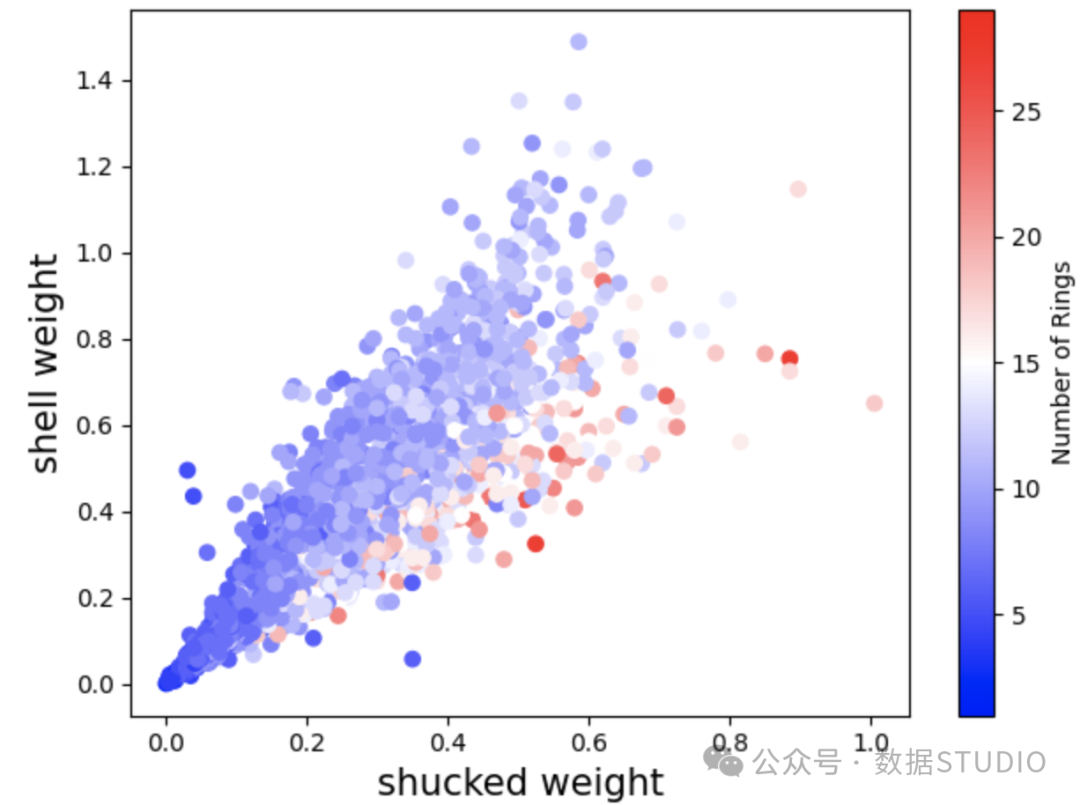图 7：散点图显示壳重和去壳重量之间的相互作用

因此，尽管存在多重共线性，该方法仍然产生了一些有价值的结果。这是一个教训，虽然你应该避免在模型中包含高度相关的特征，但它们不一定是模型无关方法的终点。你只需使用其他方法验证结果即可。

我们看到了整体、成对和非标准化 h-stat 如何协同工作，以提供模型中交互的清晰视图。但是，与所有方法一样，它们也有其局限性。为了抵消这些局限性，值得应用其他XAI]方法来分析交互。