CMU清华教LLM练成数学高手，LeanSTaR训练模型边思考边证明，登顶新SOTA

如果想训练LLM证明定理的能力，你会怎么做？

既然模型可以通过海量语料学会生成文本，那如果我们能喂给它足够数量的形式证明数据，定理证明能力自然水到渠成？

然而，我们看到的事实是，无论用符号形式还是自然语言，GPT等大模型的推理能力都不如人意。

两句话，让LLM逻辑推理瞬间崩溃！最新「爱丽丝梦游仙境」曝出GPT、Claude等重大缺陷

就像GPT-4o自信表示13.11比13.8大一样，AI再聪明却依旧会在简单的算术上犯蠢。

然而，LLM的数学能力弱，不代表自动化的定理证明器对数学没用。

前段时间刚刚被破解的「忙碌海狸」问题中，4万行Coq代码功不可没。

陶哲轩也曾在采访中强调，使用Lean等自动化工具可以彻底颠覆数学家们的工作方式。这是一股不可小觑的力量。

最近，CMU和清华的一项研究就致力于让LLM的「自然语言思维链」和Lean的形式化证明结合在一起。

论文地址：https://arxiv.org/abs/2407.10040

论文提出，Lean、Coq、Isabelle等基于形式语言（代码）的自动化证明方法，忽略了大量可能对推理过程有用的「非形式化信息」。

比如，每个证明步骤之前的潜在思维过程是必不可少的，但却不会形式化地体现在最终的公式和代码中。

比如，图1中右侧的推理思路，在左侧的证明步骤中完全「无处安放」。

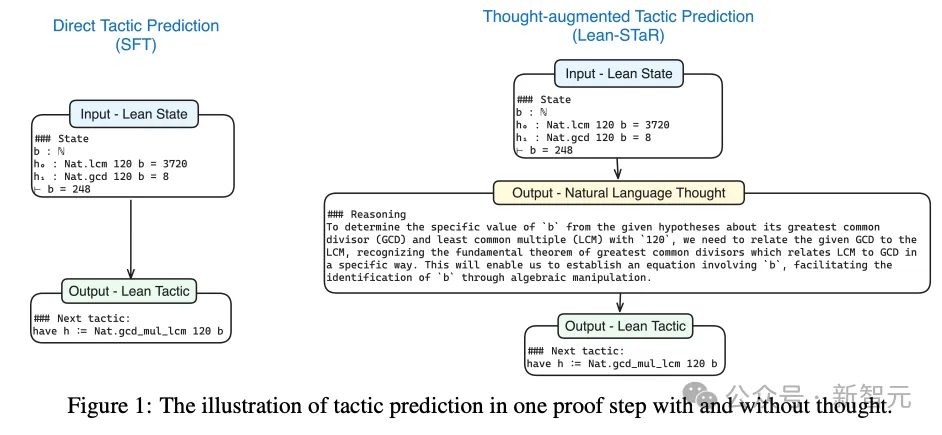
因此，作者提出了Lean-STaR训练框架，让语言模型既学会逐步推理的思维，也学会形式化的证明方式。

这意味着，需要将自然语言和形式语言交织在一起，也将「思考」和「证明」的过程交织在一起。

方法：Lean-STaR

顾名思义，Lean-STaR这个方法同时结合了之前的两项成果——Lean和STaR。

Lean是一种函数式编程语言，可以用作交互式定理证明器（Interactive Theorem Prover）。

项目主页：https://lean-lang.org/

这是由Leonardo de Moura在微软研究院期间发起的开源项目，目前已经更新到Lean 4。

比如，要想形式化证明，能从n≤m推断出n+k≤m+k，就可以用Lean写为如下形式（图6）：

首先给出一种高级的「策略」（tactic，图中所示为归纳策略k），将当前要证明的目标状态简化为多个子目标（下图中的case 0和case ih）。

这些子目标又会形成新的「状态」（state）。当所有子目标都得到证明时，我们就给出了定理的完整证明。

STaR则是来源于斯坦福和谷歌研究院在2022年发表的一篇论文，全称是「自学推理器」（Self-Taught Reasoner）。

论文地址：https://arxiv.org/abs/2203.14465

其基本思想就是用到了「自举法」（bootstrapping）。

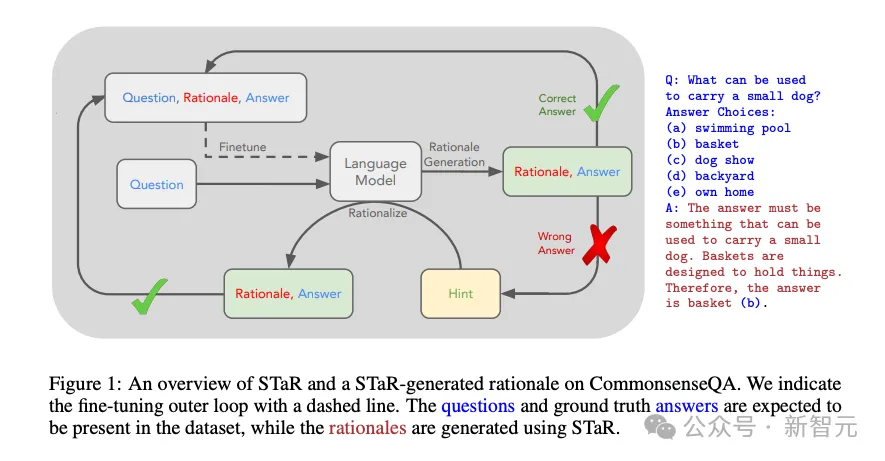
首先根据训练数据中的问题和答案，提示语言模型，生成能解释答案的「原理」（rationale）。

之后，再用这个包含了问题、答案和原理的混合数据集对LM进行微调，提升模型的推理能力（图1）。

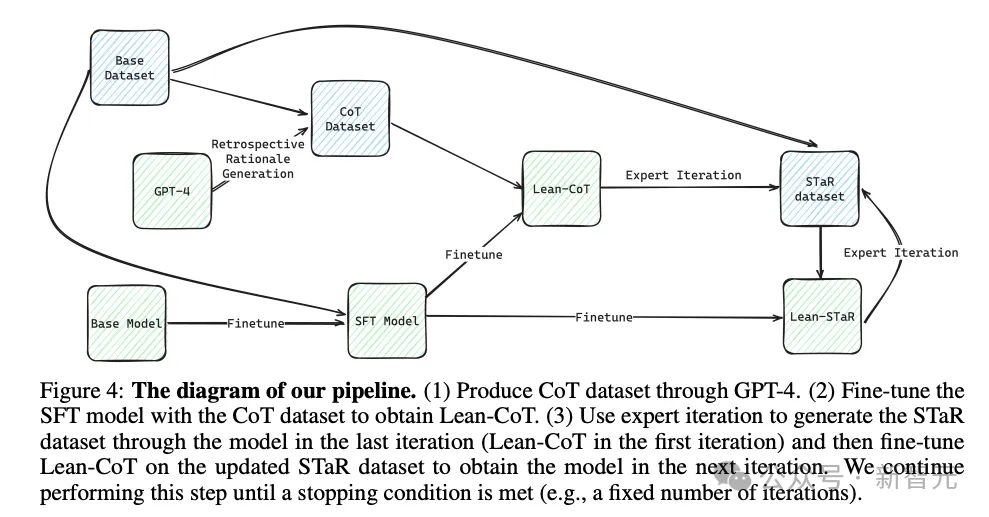
Lean-STaR模型的微调也是采用了「渐进优化」的思路，逐步将以上两个相关工作的成果融合在一起，完善底层的策略预测模型。模型构建的流水线如图4所示。

直接策略预测（Direct Tactic Prediction）

首先，将定理证明问题简单地定义为马尔科夫决策过程（MDP）。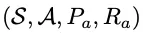

从这个角度来看，证明过程是状态s_i、策略a_i和奖励r_i∈R等3个变量组成的轨迹(s₁，a₁，r₁) (s₂，a₂，r₂)⋯其中，ITP（比如Lean）用于提供每个新状态s_i+1。

在这种经典设置中，证明定理的过程包括向LM提供状态s，让模型M生成策略𝜋_𝑀⁢(𝑎|𝑠) 。

因此，可以使用仅包含成功证明轨迹的基本数据集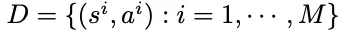

对基本模型进行监督微调，得到SFT模型。

思维增强策略预测（Thought-augmented Tactic Prediction）

结合之前所述的研究动机，我们假设「潜在想法」可以提高模型的策略预测能力，因此引入一个表示「思维」的隐变量t_i，然后将模型扩展为：

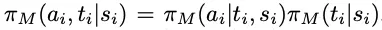
此时，根据状态预测下一个策略的分布可以表示为：

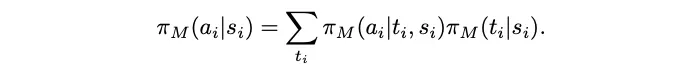
如果用这种方式预测，我们就需要一个全新的数据集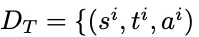

用于训练模型M，然而Lean给出的证明步骤只包含s_i和a_i。

论文的解决方法是：借助一个强大的语言模型G（如GPT-4）作为「预言家」，让它在给定当前状态s_i和真实策略a_i的情况下生成t_i，从而创建出新的数据集D_T（即图4中的CoT Dataset）。

作者将这种方法称为「回顾性原理生成」（retrospective rationale generation）。

将SFT模型在D_T数据集上再进行一次微调后，就得到了第一个思维增强的策略预测模型Lean-CoT。

自举思维增强定理证明（Bootstrapping Thought-augmented Theorem Proving）

在Lean-CoT模型的基础上，作者提出，可以应用「专家迭代」（expert iteration）方法进一步提升性能。

具体来说，从初始的Lean-CoT模型M₀以及初始数据集D开始，让M₀对每个问题进行K次采样，每次采样都会产生一个证明轨迹 [(s₀,t₀,a₀),(s₁,t₁,a₁),⋯,(s_n,t_n,a_n)]，之后过滤出成功的证明轨迹并去重，得到新数据集D₁。

接下来，在数据集D_T∪D₁上进一步微调M₀模型以得到Lean-STaR模型M₁。

将上述过程进行多次迭代，即可不断更新Lean-STaR模型。

评估实验

为了测试Lean-STaR的具体性能，研究使用了可用的最佳开放语言模型Lean语料库 (InternLM2-Math-base-7b) 上进行预训练，并遵循Lean的Mathlib作为底层训练集的标准实践。

首先以LeanDojo Benchmark 4 v9作为监督微调(SFT)数据集，包含超过23.1万个示例，进行1轮微调以获得SFT模型。

之后从数据集中随机选择17256个不同的成功证明轨迹，并使用GPT-4-0125模型注释出52438个想法，并且执行两次专家迭代。

实验在MiniF2F基准上评估Lean-STaR，使用了与之前的实验工作类似的评估设置，但主要使用的是采样方法（sampling）而不是最佳优先搜索（best-first search）来进行评估。

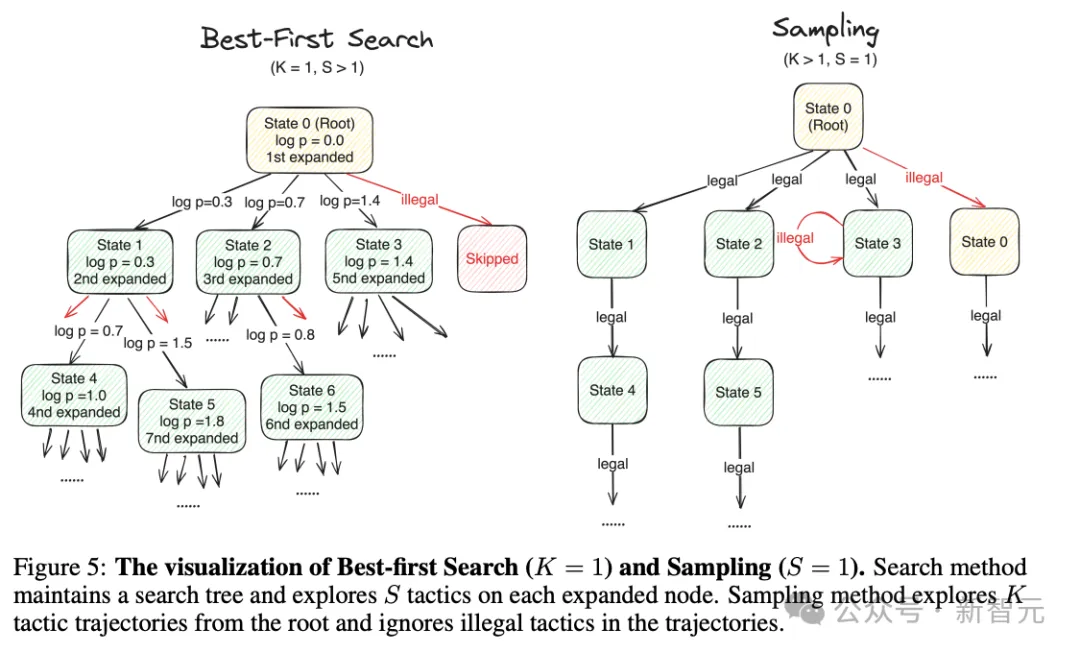
实验结果表明，回顾性原理生成和专家迭代都显著提高了模型的定理证明能力。

实验结果

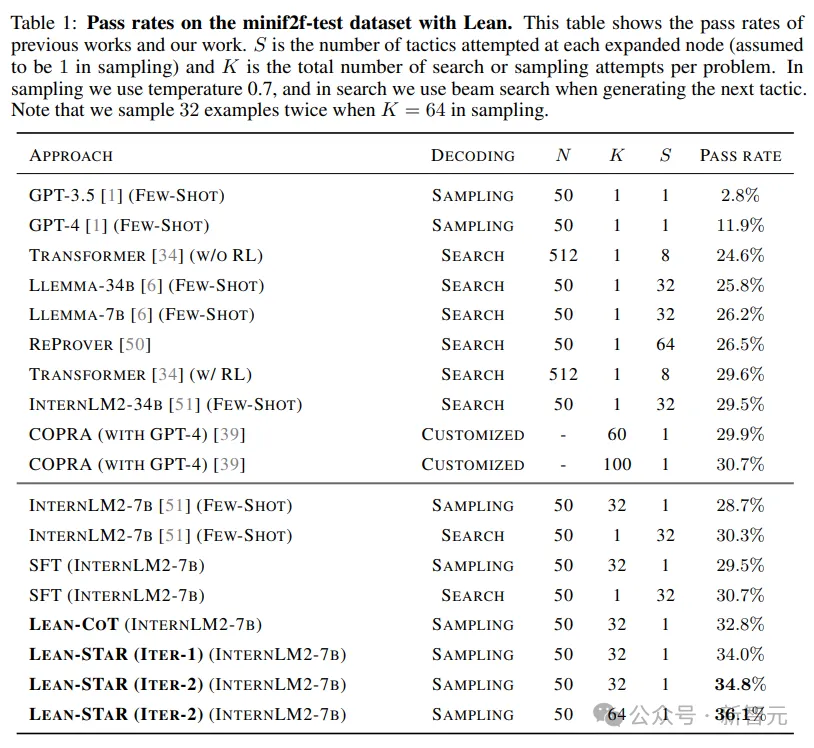
实验的主要结果如下表所示，Lean-STaR比之前基于Lean的SOTA模型有了显著的改进。

例如，在类似的推理预算下，同样使用best-first search，Lean-STaR从InternLM2的30.3%提升至34.8%，也同样高于使用GPT-4的COPRA（30.7%）。

随着计算预算的增加，Lean-STAR的性能进一步提升至36.1%。

思维增强改进定理证明

Lean-STaR的第一阶段在思维增强的合成数据集上进行微调，训练模型来交替生成思维和策略。

此阶段的微调模型（在表1中表示为Lean-CoT）达到了32.8%的通过率，高于此阶段之前的模型（表示为 SFT，29.5%）。

可以证明，第一阶段的思维增强能提高语言模型的定理证明能力，即使对于已经专门用于生成Lean策略的语言模型（例如SFT）也依旧成立。

自举法（Bootstrapping）进一步改进

Lean-STaR的第二阶段包括使用当前语言模型生成新的思维和策略，保存正确结果，并结合初始数据集进行训练。

从表1结果来看，每次迭代都会提高模型的定理证明性能，从32.8%（初始模型）到34%（迭代1次后的L-STR）再到34.8%（迭代2次后的L-STR）。

此外，我们发现该模型可以通过额外采样进一步改进，将采样的K值加倍后，分数能进一步提升至36.1%。

无CoT的专家迭代实验

表5显示了没有CoT的专家迭代结果（即仅使用状态和策略，没有思维增强），对比Lean-CoT和Lean-STaR的表现。

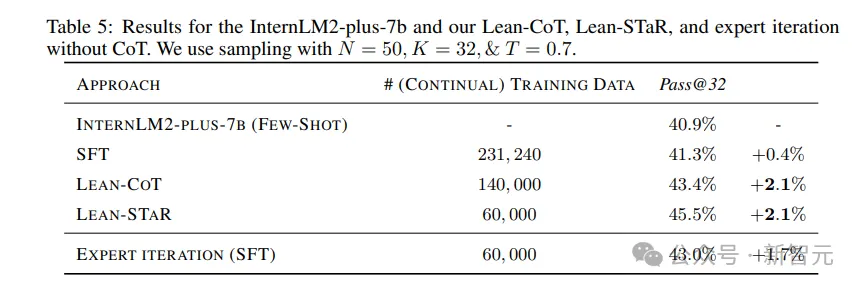
仅用专家迭代时，准确率就达到了43.0%，低于Lean-STaR (45.5%)。

这表明Lean-STaR的性能提升不仅仅来自于专家迭代的使用，思维增强也有不可忽略的效果。

问题类型与难度

MiniF2F-test中的问题有多个来源，包括AIME、AMC、IMO等数学竞赛以及MATH数据集，并进行了手动形式化处理。

这些问题可能有不同的难度和类型。表2展示了成功证明的问题数量，按类型和难度划分。

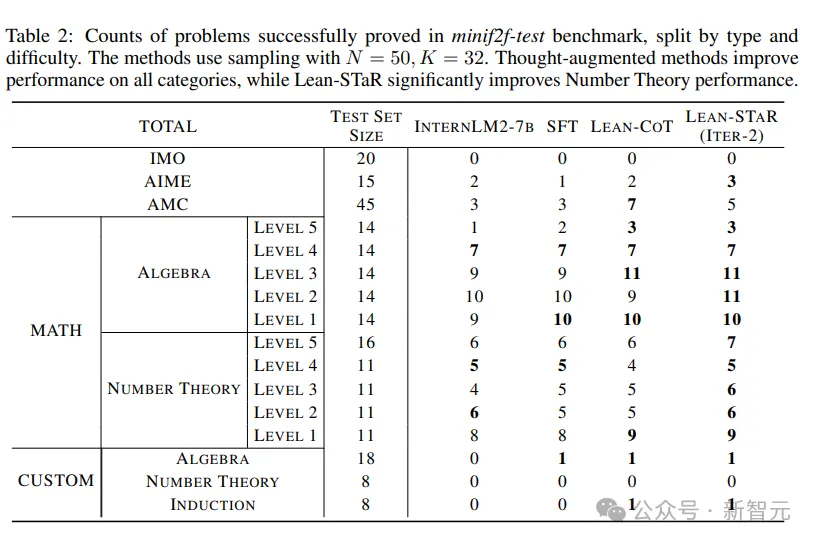
Lean-CoT提高了解决所有类别难题的表现，尤其是数学竞赛中的难题。

除了这些改进之外，Lean-STAR的改进主要集中在数论方面。

搜索和抽样预算

表4说明了问题通过率与搜索规模或抽样预算S×K的关系。

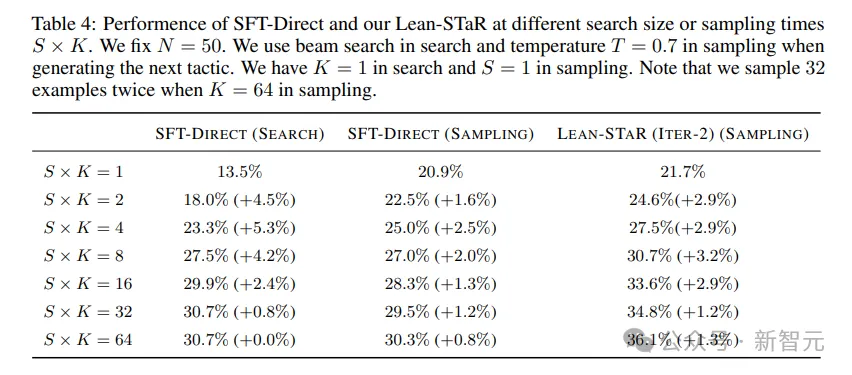
实验发现，Lean-STAR性能与K值的大小成正比，特别是当K值相对较大时。

对比前两列和Lean-STaR可以发现，附带思维的额外采样能提高定理证明性能，而没有思维的额外采样可能会饱和。

作者猜测，可能是因为「思维」增加了输出的多样性，并有助于对定理证明空间进行探索。

因此，Lean-STaR更具可扩展性（就推理阶段算力而言），并且可以通过额外的专家迭代进一步改进。

更强基础模型和更多数据实验

实验还使用了更强的语言模型InternLM2-Math-plus-7b训练LeanSTaR，来测试不同语言模型性能的影响。

不仅基座模型更强，为数据集注释「思维」的模型也从GPT-4升级到GPT-4o，生成了1.4万条想法。

实验只执行一次专家迭代，收集了大约6万条（证明状态、思维、下一步策略）正确的数据，命名为「STaR 数据集」。

在STaR数据集上进一步微调得到Lean-STAR模型，其测评结果如表3所示，可以看到Lean-STaR仍然比基线有了显著的改进。

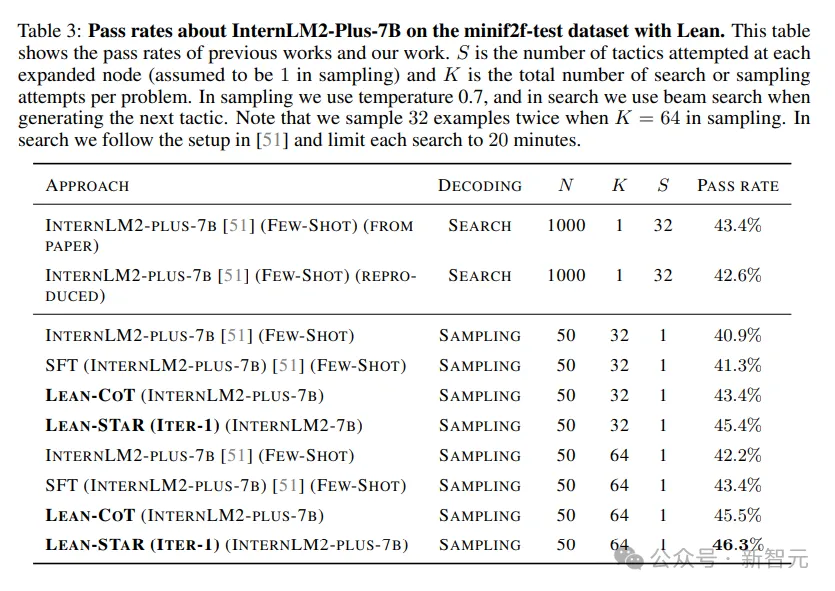
结论和局限性

研究团队提出了Lean-STaR，这是一种新颖的方法，通过将思维链 (CoT) 原理集成到每个证明步骤中，显著增强了语言模型用形式化数学语言进行定理证明的能力。

方法首先根据ground truth回顾性地为证明步骤生成「原理」，然后微调语言模型，训练模型学会生成「原理」并预测后续策略，从而得到Lean-CoT模型。

然后使用专家迭代进一步改进该模型，根据被证明为正确的采样结果进行微调，并使用Lean solver进行验证。

研究的贡献包括引入第一个思维增强的定理证明数据集，并证明专家迭代可以进一步提高性能。得到的模型在miniF2F测试上取得最新SOTA，将通过率从30.3%提高到36.1%。

这些进步不仅提高了自动化定理证明的准确性，而且还提供了一个可扩展且高效的框架来促进对数学的理解，这可能会对教育、科学发现和程序验证产生重大影响。

方法的主要限制在于，其性能可能受限于计算可扩展性，实验中用于微调Lean-CoT和Lean-STaR模型的数据集都不是很大。

需要注意的是，专家迭代的速度也存在严重瓶颈，会受限于Lean ITP的缓慢进程。

此外，使用GPT-4生成合成数据成本较大，并可能引入偏差。