今天给大家分享一个超强的算法模型,DBSCAN
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法,常用于识别空间数据中的任意形状的聚类,同时能够有效地处理噪声数据。
它不需要预先指定簇的数量,这与 K-means 等算法不同。
核心思想
DBSCAN 通过分析数据点在空间中的密度,自动识别簇。
它的基本思想是:对于一个数据集中的每个点,通过计算其邻域内点的数量来确定其是否位于簇的高密度区域中。
 图片
图片
关键参数
DBSCAN 依赖于两个关键参数:
- ε(eps)
用于定义一个点的邻域的半径。该值决定了一个点与另一个点是否是密切相关的。 - MinPts
一个点的邻域中至少需要包含的点的数量(包括该点自身),以将其视为核心点。
关键术语
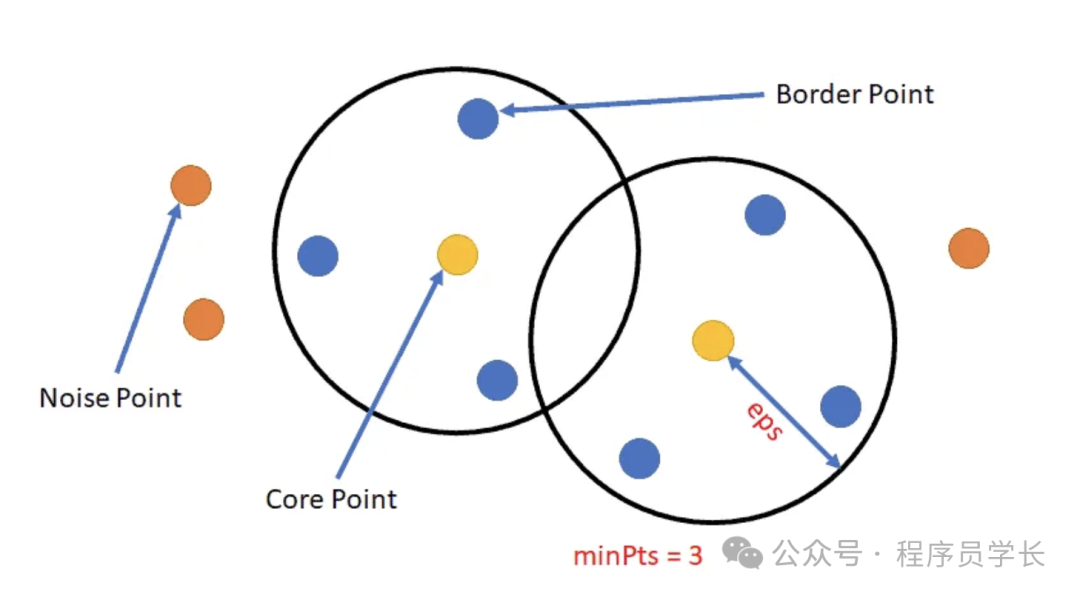
- 核心点(Core Point)
如果一个点的邻域中包含至少 MinPts 个点,则该点是核心点。 - 边界点(Border Point)
一个点不满足核心点的条件,但位于一个核心点的邻域内。 - 噪声点(Noise Point)
既不是核心点也不是边界点。
算法步骤
- 初始化
从数据集中随机选择一个未访问的数据点。 - 邻域搜索
对于每个数据点,DBSCAN 会找到其 ε 邻域内的所有点。 - 核心点识别
如果某个点在其 ε 邻域内至少有 MinPts 个邻居,则该点被归类为核心点。这些点构成了聚类的中心。 - 聚类形成
DBSCAN 从核心点开始,并递归访问其密度连通的邻居(彼此 ε 邻域内的点)。
所有核心点及其密度可达的邻居都被分配到同一个聚类中。 - 边界点分配
边界点被分配到与其关联的核心点相同的簇。 - 噪声分类
任何既不是核心点也不是边界点的点都被视为噪声点或异常值。这些点不属于任何聚类。
示例代码
下面是一个使用 Python 的 Scikit-learn 库实现 DBSCAN 的示例代码。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN
# 生成示例数据
X, _ = make_moons(n_samples=300, noise=0.05, random_state=0)
# 应用 DBSCAN 算法
dbscan = DBSCAN(eps=0.2, min_samples=5)
labels = dbscan.fit_predict(X)
# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('DBSCAN Clustering')
plt.show() 图片
图片
优缺点
优点
- 没有预定义聚类数
与 K-Means 不同,DBSCAN 不需要指定聚类数,因此适用于聚类结构未知的数据 - 对异常值具有鲁棒性
DBSCAN 可以有效处理位于密集区域之外的异常值并将其标记为噪声 - 灵活的形状检测
DBSCAN 可以找到任意形状的聚类,而 K-Means 则仅限于球形聚类
缺点
- 参数敏感性,性能可能因 ε 和 MinPts 的选择而异
- 时间复杂度高
- 对于大型数据集来说,计算距离和识别核心点的计算成本可能很高












































