使用TLA+形式化验证Go并发程序

Writing is nature's way of letting you know how sloppy your thinking is - Guindon

在2024年6月份举办的GopherCon Europe Berlin 2024[1]上，一个叫Raghav Roy的印度程序员(听口音判断的)分享了Using Formal Reasoning to Build Concurrent Go Systems[2]，介绍了如何使用形式化验证工具TLA+[3]来验证Go并发程序的设计正确性。

TLA+是2013年图灵奖获得者、美国计算机科学家和数学家、分布式系统奠基性大神、Paxos算法[4]和Latex[5]的缔造者Leslie B. Lamport[6]设计的一种针对数字系统(Digital Systems)的高级(high-level)建模语言，TLA+诞生于1999年，一直低调演进至今。

TLA+不仅可以对系统建模，还可以与模型验证工具，比如：TLC model checker，结合使用，对被建模系统的行为进行全面的验证。我们可以将TLA+看成一种专门用于数字系统建模和验证的DSL语言[7]。

注：TLA是Temporal Logic of Actions的首字母缩写，Temporal Logic[8]，即时序逻辑，是一种用于描述和推理系统行为随时间变化的逻辑框架，由Arthur Prior在1950年代后期引入逻辑学。在后面对TLA+的进一步介绍中，大家可能就会逐渐理解为什么Lamport给这门语言命名为TLA+了。

这不是我第一次接触TLA+，去年就花过一些时间了解过TLA+的资料，可能是因为姿势不够正确，没有在本博客留下只言片语，而这次我打算写点有关TLA+的东西。

1. 为什么需要TLA+

从1999年Lamport发表的论文“Specifying Concurrent Systems with TLA+[9]”以及他2014年在微软的演讲“Thinking Above the Code[10]”中 ，我们大致可以得到Lamport在20多年前设计TLA+的朴素的动机：**期望程序员能像科学家一样思考，在编码之前用一种精确的形式化的语言写出目标系统的spec，这个过程类似于建筑架构师在建筑施工之前编制建筑的蓝图(blueprint)**。

为什么要编写目标系统的spec呢？

综合来自Lamport的相关资料，大致可以梳理出以下两点：

• 从程序员的角度来看，在开始编码之前，先在抽象的层面思考系统行为，而不是过早地陷入编程语言的具体语法中。并且先写下规格说明，可以帮助程序员明确需求，认知系统，发现潜在问题，并为后续的编码和维护提供指导。
• 从系统复杂性的角度来看，对于日益复杂的并发和分布式系统，仅靠直觉思考很难保证正确性，传统的测试方法也已经不足以发现所有问题。这时候写spec(规格说明)并用配套的检查工具进行验证就变得非常必要。

那为什么要新设计TLA+来写spec呢，而不是使用像C++这类编程语言，或是其他已存在的形式化语言来编写spec呢？

Lamport给出的理由有以下几个：

• 编程语言的局限性：像C++这样的编程语言主要是为了实现而设计的，而不是为了spec。它们往往过于关注实现细节，而不是高层次的系统行为，缺乏描述并发和分布式系统所需的抽象能力，不适合表达系统的时序性质和不变量。
• 已有形式化语言的不足：当时存在的其他形式化语言大多存在要么过于学术化，难以在实际工程中应用，要么难以自然地表达并发和分布式系统的特性等问题；并且缺少工具支持，不具备spec验证功能。
• 数学建模的局限：纯粹的数学公式虽然精确，但对非数学背景的工程师来说难以理解和使用，缺乏工具支持，难以自动化验证，难以直接映射到系统设计和实现。

Lamport设计的TLA+是建立在坚实的数学基础之上，这使得它能够支持严格的数学推理和证明与自动化验证工具（如TLC模型检查器）无缝集成。TLA+被设计为在高度抽象的层面描述系统，不会像编程语言那样受实现细节的束缚。此外，结合时序逻辑和状态机，TLA+可以描述并发和分布式系统，并在设计层面验证系统的正确性。

根据Lamport的不完全统计[11]，TLA+在Intel、Amazon、Microsoft等大厂都有应用，一些知名的算法以及开源项目也使用TLA+进行了形式化验证，比如Raft算法的作者就给出了Raft算法的TLA+ spec[12]，国内分布式数据库厂商pingcap也在项目中使用TLA+对raft算法以及分布式事务做了形式化的验证[13]。

在这些应用案例中，AWS的案例是典型代表。AWS也将应用TLA+过程中积累的经验以paper的形式发表了，其论文集合[14]也被Lamport放置在其个人主页上了。从这些论文内容来看，AWS对TLA+的评价是很正面的：AWS使用TLA+对10个大型复杂的真实系统进行建模和验证，的确发现了多个难以通过其他方法发现的微妙错误。同时，通过精确描述设计，TLA+迫使工程师更清晰地思考，消除了“看似合理的含糊之处”。此外，AWS工程师认为TLA+ spec也是一种很好的文档形式，可以提供精确、简洁、可测试的设计描述，有助于新人快速理解系统。

铺垫了这么多，TLA+究竟是什么？它是如何在高级抽象层面对分布式系统和并发系统进行描述和验证的？接下来，我们就来看一下。

2. Lamport对TLA+的定义

在Lamport的论文、书籍以及一些演讲资料中，他是这么定义TLA+的：A language for high-level modeling digital systems。对于这个定义，我们可以“分段”来理解一下。

• Digital System

什么是TLA+眼中的数字系统(Digital System)？Lamport认为数字系统包括算法(Algorithms)、程序(Programs)和计算机系统(Computer system)，它们有一个共同特点，那就是可以抽象为一个按离散事件序列(sequence of discrete events)进行持续执行和演进的物理系统，这是TLA+后续描述(specify)数字系统的基础。随着多核和云计算的兴起，并发程序和分布式的关键(critical)系统成为了TLA+的主要描述对象，这样的系统最复杂，最难正确实现，价值也最高，值得使用TLA+对其进行形式化的验证。

• High Level

TLA+面向设计层面，在代码实现层面之上，实施于编写任何实现代码之前。此外，High Level也意味着可以忽略那些系统中不是很关键(less-critical)的部分以及低层次的实现细节。

去除细节进行简化的过程就是抽象（Abstraction），它是工程领域最重要的环节。抽象可以让我们理解复杂的系统，如果不了解系统，我们就无法对系统进行正确的建模并实现它。

而使用TLA+编写系统spec其实就是一个学习对系统进行抽象的过程，学会抽象思考，可以帮助工程师提高设计能力。

• Modeling

TLA+是通过描述系统的行为(behavior)来对数字系统进行建模的。那么什么是系统的行为呢？如下图所示：

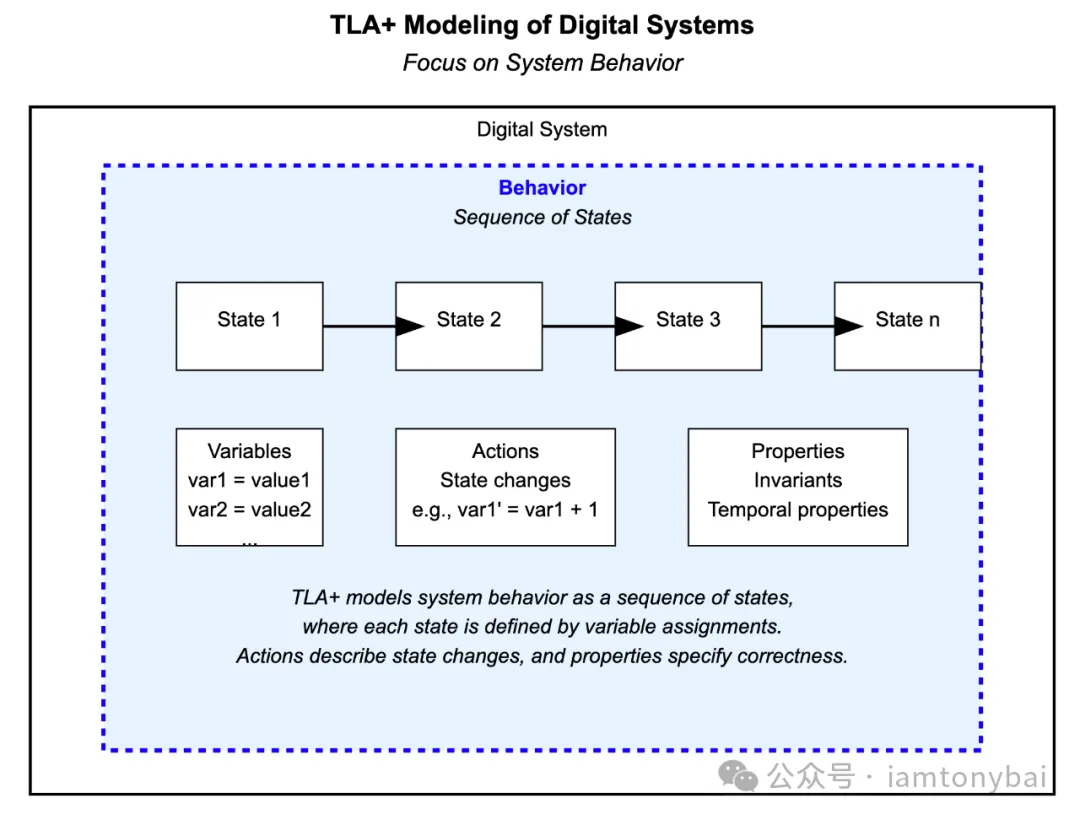此图由claude sonnet 3.5根据我的prompt生成

行为被Lamport定义为一系列的状态（Sequence of States），这些状态仍然按顺序排列，表示系统随时间的演变。而状态本身则是对变量的赋值。状态之间的转换由动作(action)描述，而系统的正确性由属性(properties)指定。

这种方法特别适合建模并发和分布式系统，因为它允许我们精确地描述系统的所有可能行为，包括不同组件之间的交互和可能的竞争条件，如下图所示：

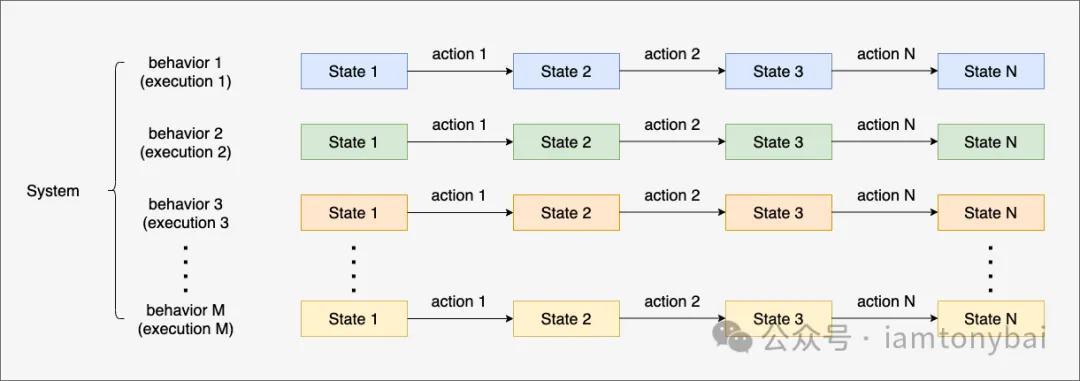图片

在TLA+中，属性(properties)是用来描述系统应该满足的条件或特性，它们在验证系统行为的正确性方面起着关键作用。我们所说的系统工作正常就是指这些在执行过程中的属性都得到了满足。

在TLA+中，有两类属性是我们特别需要关注的，一类是安全属性（Safety Properties），一类则是活性属性（Liveness Properties）。前者确保“坏事永远不会发生”，比如使用不变量在并发系统中确保两个进程不会同时进入临界区；后者则是确保“好事最终会发生”，在分布式系统中的最终一致性（eventual consistency）是一个活性属性，它保证系统最终会达到一致的状态。TLA+允许我们精确地指定这些属性，然后使用TLC模型检查器来验证系统是否满足这些属性。这种方法特别适合于复杂的并发和分布式系统，因为它能够发现在传统测试中难以发现的微妙错误。

注：关于TLA+可以用来形式化描述(specify)和验证(check)数字系统的底层数学理论，可以参考Lamport老爷子那本最新尚未完成的书籍A Science of Concurrent Programs(2024.6.7版)[15]。

接下来，我们就来看看TLA+究竟如何编写。不过直接介绍TLA+语法比较抽象和枯燥，在我读过的TLA+语法资料中，Lamport在The TLA+ Video Course[16]第二讲中将一个C示例程序一步一步像数学推导一样转换为TLA+语法的讲解对我帮助非常大，我觉得有必要将这个示例放到这篇文章中。

3. 从C代码到TLA+：转换步骤详解

Lamport的这个过程展示了如何从一个具体的编程语言实现(以C代码为例)逐步抽象到一个数学化的、更加通用的系统描述。每一步都增加了抽象级别，最终得到一个可以用于形式化验证的TLA+规范(spec)。以下是这个演进过程的主要阶段：

3.1 初始C程序分析

下面是这个示例的原始C代码：

int i;
void main() {
    i = someNumber();
    i = i + 1;
}

这不是一个并发程序，它只有一个执行路线(execution)，前面说过，一个行为(execution)是一个状态序列，我们就来定义这个状态序列以及它们之间的转换关系。

我们先识别出程序的状态变量：i以及引入的控制状态变量（PC），PC变量来表示程序的执行位置。接下来我们就来描述一个可以代码该程序所有状态的“状态机”。

3.2 状态机描述

该程序可以划分为三个状态：

• 初始状态：i = 0, PC = "start"
• 中间状态：i in {0, 1, ..., 1000}(这里限定了someNumber函数返回的数值范围), PC = "middle"
• 结束状态：i = i + 1, PC = "done"

下面用自然语言描述一下上述状态的转换关系：

if current value of pc equals "start"
    then next value of i in {0, 1, ..., 1000}
         next value of pc equals "middle"
    else if current value of pc equals "middle"
            then next value of i equals current value of i + 1 
                 next value of pc equals "done"
            else no next values

接下来，我们就来将上述对于状态转换的描述变换一下，尽量用数学来表示。

3.3 转换为数学表示

这里的转换分为几步，我们逐一来看。

• 换掉"current value of"

if pc equals "start"
    then next value of i in {0, 1, ..., 1000}
         next value of pc equals "middle"
    else if pc equals "middle"
            then next value of i equals i + 1 
                 next value of pc equals "done"
            else no next values

替换后，pc即the current value of pc，i即current value of i。

• 换掉"next value of"

我们用i'换掉"next value of i", 用pc'换掉"next value of pc"，结果如下：

if pc equals "start"
    then i' in {0, 1, ..., 1000}
         pc' equals "middle"
    else if pc equals "middle"
            then i' equals i + 1 
                 pc' equals "done"
            else no next values

• 用"="符号换掉equals

替换的结果如下：

if pc = "start"
    then i' in {0, 1, ..., 1000}
         pc' = "middle"
    else if pc = "middle"
            then i' = i + 1 
                 pc' = "done"
            else no next values

• 将in换为数学符号∈

if pc = "start"
    then i' ∈ {0, 1, ..., 1000}
         pc' = "middle"
    else if pc = "middle"
            then i' = i + 1
                 pc' = "done"
            else no next values

3.4 TLA+语法转换

• 将集合表示换为正式的数学符号

{0, 1, ..., 1000}并非数学表示集合的方式，替换后，结果如下：

if pc = "start"
    then i' ∈ 0..1000
         pc' = "middle"
    else if pc = "middle"
            then i' = i + 1
                 pc' = "done"
            else no next values

这里0..1000使用了TLA+的集合表示语法。

• 转换为单一公式(formula)

将C代码转换为上面的最新代码后，你不要再按照C的语义去理解上述转换后的代码了。新代码并非是像C那样为了进行好一些计算而编写的一些指令，新代码是一个关于i、pc、i'和pc'的公式(formula)，这是理解从C带TLA+的最为关键的环节，即上述这段代码整体就是一个公式！

上述代码的意思并非if pc = "start"为真，然后执行then部分，否则执行else部分。其真正含义是如果pc = "start"为真，那么上述整个公式将等于then这个公式的值，否则整个公式将等于else公式的值。

不过我们看到在上面的then子句中存在两个独立的公式，以第一个then为例，两个独立公式分别为i' ∈ 0..1000和pc' = "middle"。这两个独立的公式之间是and的关系，我们需要将其转换为一个公式。TLA+中使用"/"表示and连接，下面是使用"/"将公式连接后的结果：

if pc = "start"
    then (i' ∈ 0..1000) /\
         (pc' = "middle")
    else if pc = "middle"
            then (i' = i + 1) /\
                 (pc' = "done")
            else no next values

• 改造else公式

问题来了! 当存在某个状态，使得整个公式等于最后一个else公式的值时，我们发现这个值为"no next values"，而前面的then、else if then公式的值都为布尔值TRUE或FALSE。这里最后的ELSE公式，它的值应该为FALSE，无论i、pc、i'和pc'的值为什么，因此这里直接将其改造为FALSE：

if pc = "start"
    then (i' ∈ 0..1000) /\
         (pc' = "middle")
    else if pc = "middle"
            then (i' = i + 1) /\
                 (pc' = "done")
            else FALSE

• TLA+的关键字为大写且TLA+源码为ASCII码

if、then、else 这些都是TLA+的关键字，而TLA+的关键字通常为大写，并且TLA+源码为ASCII码，∈需换成\in。这样改变后的结果如下：

IF pc = "start"
    THEN (i' \in 0..1000) /\
         (pc' = "middle")
    ELSE IF pc = "middle"
            THEN (i' = i + 1) /\
                 (pc' = "done")
            ELSE FALSE

到这里，我们就得到了一个美化后的的TLA+公式了!

3.5 干掉if else

前面说过，我们将C代码改造为了一个公式，但公式中依然有if else总是感觉有些格格不入，是不是可以干掉if else呢！我们来试一下！

我们先用A、B替换掉then语句中的两个公式:

IF pc = "start"
    THEN A
    ELSE IF pc = "middle"
            THEN B
            ELSE FALSE

如果整个公式为TRUE，需要(pc = "start")和A都为TRUE，或(pc = "middle")和B都为TRUE。TLA+引入一个操作符/表示or，这样整个公式为TRUE的逻辑就可以表示为：

((pc = "start") /\ A) 
\/ ((pc = "middle") /\ B)

好了，现在我们再把A和B换回到原先的公式：

((pc = "start") /\  
    (i' \in 0..1000) /\
    (pc' = "middle"))
\/ ((pc = "middle") /\ 
    (i' = i+1 ) /\
    (pc' = "done"))

你是不是感觉不够美观啊！TLA+提供了下面等价的、更美观的形式：

\/ /\ pc = "start"
   /\ i' \in 0..1000
   /\ pc' = "middle"
\/ /\ pc = "middle"
   /\ i' = i+1 
   /\ pc' = "done"

这种形式完全去掉了括号，并可以像列表一样表达公式！并且无论是/\还是/都是可交换的(commutative)，顺序不影响公式的最终结果。

3.6 完整的TLA+ spec

从数学层面，上面C代码将被拆分为两个公式，一个是初始状态公式，一个是下个状态的公式：

初始状态公式：(i = 0) /\ (pc = "start")
下一状态公式：
              \/ /\ pc = "start"
                 /\ i' \in 0..1000
                 /\ pc' = "middle"
              \/ /\ pc = "middle"
                 /\ i' = i+1 
                 /\ pc' = "done"

但对于一个完整的TLA+ spec来说，还需要额外补充些内容：

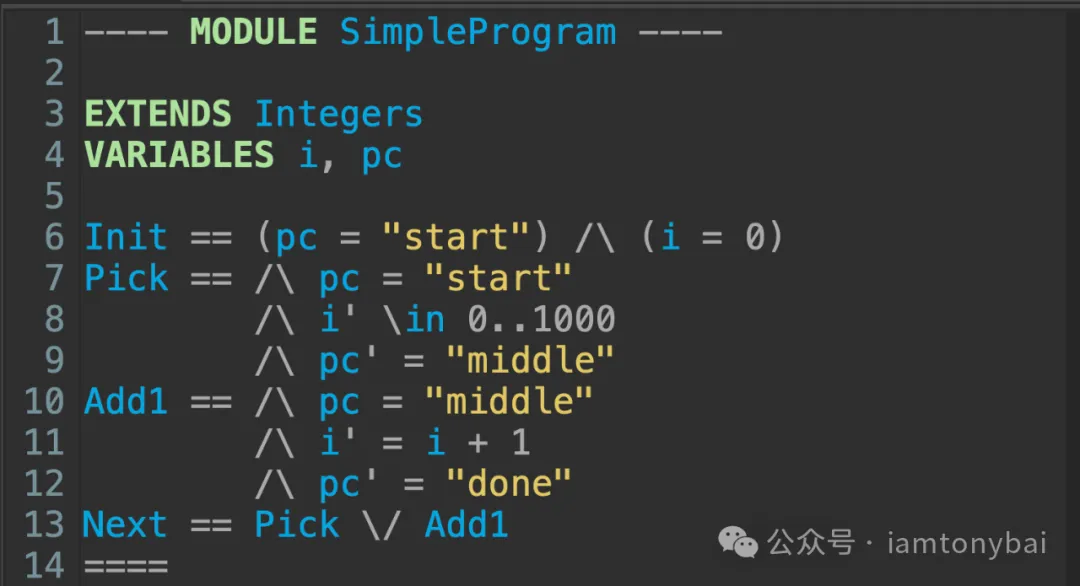
---- MODULE SimpleProgram ----

EXTENDS Integers
VARIABLES i, pc

Init == (pc = "start") /\ (i = 0)
Next == \/ /\ pc = "start"
           /\ i' \in 0..1000
           /\ pc' = "middle"
        \/ /\ pc = "middle"
           /\ i' = i + 1
           /\ pc' = "done"
====

一个完整的TLA+ spec是放在一个module中的，上面例子中module为SimpleProgram。TLA toolkit要求tla文件名要与module名相同，这样上面代码对应的tla文件应为SimpleProgram.tla。

EXTENDS会导入TLA+内置的标准module，这里的Integers就提供了基础的算术运算符，比如+和..。

VARIABLES声明了状态变量，比如这里的i和pc。变量加上'即表示该变量的下一个状态的值。

接下来便是公式的定义。Init和Next并非固定公式名字，你可以选择任意名字，但使用Init和Next是惯用法。

"===="用于标识一个module的Body内容的结束。

对于上面简单的C程序，这样的spec是可以的。但在实际使用中，spec中的Next一般会很长，一个好的实践是对其进行拆分。比如这里我们就将Next拆分为两个子公式：Pick和Add1：

---- MODULE SimpleProgram ----

EXTENDS Integers
VARIABLES i, pc

Init == (pc = "start") /\ (i = 0)
Pick == /\ pc = "start"
        /\ i' \in 0..1000
        /\ pc' = "middle"
Add1 == /\ pc = "middle"
        /\ i' = i + 1
        /\ pc' = "done"
Next == Pick \/ Add1
====

4. 使用TLA+ Toolkit验证spec

Lamport提供了TLA+的Module Checker，我们可以从其主页提供的工具包下载链接[17]下载TLA+ Toolkit。

先将上面的TLA+ spec存入一个名为SimpleProgram.tla的文件。然后打开TLA+ Toolkit，选择File -> Open spec -> Add New Spec...，然后选择你本地的SimpleProgram.tla即可加载该spec：

图片

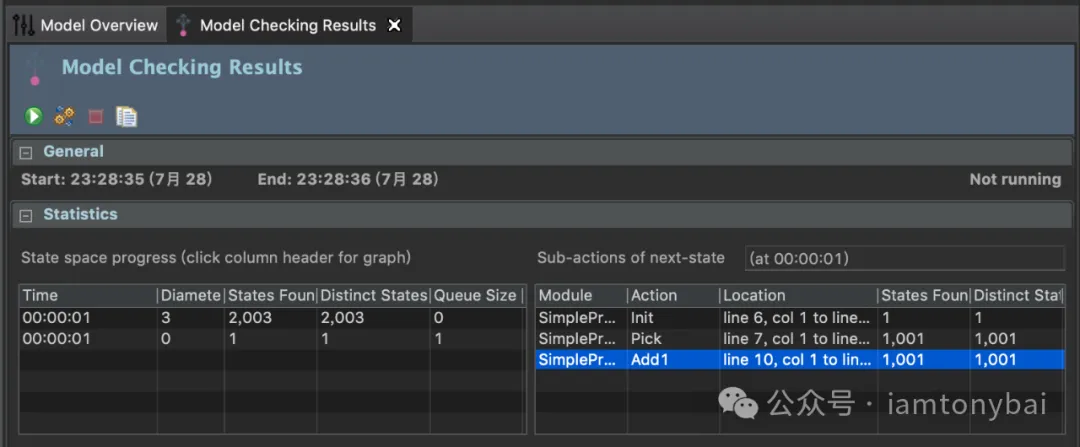
之后，我们可以点击菜单项“TLC Model Checker” -> New Model，便可以为该tla建立一个model配置(去掉deadlock)，运行check后，你能看到下面结果：

图片

我们看到model check一共检查了2003个不同的状态。

注：TLA+还提供了一个Visual Studio Code的扩展[18]，也可以用来specify和check model。

5. 使用TLA+验证Go并发程序

Go语言因其强大的并发编程能力而备受青睐。然而，Go的并发方案虽然简单，但也并非银弹。随着并发程序复杂性的增加，开发者常常面临着难以发现和调试的错误，如死锁和竞态条件。这些问题不仅影响程序的正确性，还可能导致严重的系统故障。对于Go开发的并发系统的关键部分，采用TLA+进行形式化的验证是一个不错的提高系统正确性和可靠性的方法。

接下来，我们就建立一个生产者和消费者的Go示例，然后使用TLA+为其建模并check。理论上应该是先有设计思路，再TLA+验证设计，再进行代码实现，这里的Go代码主要是为了“描述”该并发程序的需求和行为逻辑。

// go-and-tla-plus/producer-consumer/main.go
package main

import (
 "fmt"
 "sync"
)

func producer(ch chan<- int, wg *sync.WaitGroup) {
 defer wg.Done()
 for i := 0; i < 5; i++ {
  ch <- i
 }
 close(ch)
}

func consumer(ch <-chan int, wg *sync.WaitGroup) {
 defer wg.Done()
 for num := range ch {
  fmt.Println("Consumed:", num)
 }
}

func main() {
 ch := make(chan int)
 var wg sync.WaitGroup
 wg.Add(2)

 go producer(ch, &wg)
 go consumer(ch, &wg)

 wg.Wait()
}

任何Go初学者都可以很容易读懂上面的程序逻辑：Producer生产0到4四个数，每生成一个就通过unbuffered channel发出，consumer从channel接收数字并消费。Producer生产完毕后，关闭channel。Consumer消费完所有数字后，退出，程序终止。

下面是使用TLA+编写的ProducerConsumer的完整Spec：

// go-and-tla-plus/producer-consumer/ProducerConsumer.tla

---- MODULE ProducerConsumer ----
EXTENDS Integers, Sequences

VARIABLES 
    ch,           \* 通道内容
    produced,     \* 已生产的消息数
    consumed,     \* 已消费的消息数
    closed        \* 通道是否关闭

TypeOK ==
    /\ ch \in Seq(0..4)
    /\ produced \in 0..5
    /\ consumed \in 0..5
    /\ closed \in BOOLEAN

Init ==
    /\ ch = <<>>
    /\ produced = 0
    /\ consumed = 0
    /\ closed = FALSE

Produce ==
    /\ produced < 5
    /\ ch = <<>>
    /\ ~closed
    /\ ch' = Append(ch, produced)
    /\ produced' = produced + 1
    /\ UNCHANGED <<consumed, closed>>

Close ==
    /\ produced = 5
    /\ ch = <<>>
    /\ ~closed
    /\ closed' = TRUE
    /\ UNCHANGED <<ch, produced, consumed>>

Consume ==
    /\ ch /= <<>>
    /\ ch' = Tail(ch)
    /\ consumed' = consumed + 1
    /\ UNCHANGED <<produced, closed>>

Next ==
    \/ Produce
    \/ Close
    \/ Consume

Fairness ==
    /\ SF_<<ch, produced, closed>>(Produce)
    /\ SF_<<produced, closed>>(Close)
    /\ SF_<<ch>>(Consume)

Spec == Init /\ [][Next]_<<ch, produced, consumed, closed>> /\ Fairness

THEOREM Spec => []TypeOK

ChannelEventuallyEmpty == <>(ch = <<>>)
AllMessagesProduced == <>(produced = 5)
ChannelEventuallyClosed == <>(closed = TRUE)
AllMessagesConsumed == <>(consumed = 5)

====

这个Spec不算长，但也不短，你可能看不大懂，没关系，接下来我们就来说说从main.go到ProducerConsumer.tla的建模过程，并重点解释一下上述TLA+代码中的重要语法。

针对main.go中体现出来的Producer和Consumer的逻辑，我们首先需要识别关键组件：生产者、消费者和一个通道(channel)，然后我们需要确定状态变量，包括：通道内容(ch)、已生产消息数(produced)、已消费消息数(consumed)、通道是否关闭(closed)。

接下来，我们就要定义action，即导致状态变化的step，包括Produce、Consume和Close。

最后，我们需要设置初始状态Init和下一个状态Next，并定义安全属性(TypeOK)和一些活性属性(如AllMessagesConsumed等)

现在，我们结合上述TLA+的代码，来说一下上述这些逻辑是如何在TLA+中实现的：

---- MODULE ProducerConsumer ----

这一行定义了模块名称，模块名称与文件名字(ProducerConsumer.tla)要一致，否则TLA+ Toolkit在Open Spec时会报错。

EXTENDS Integers, Sequences

这行会导入整数和序列模块，以使用相关运算符。

VARIABLES 
    ch,           \* 通道内容
    produced,     \* 已生产的消息数
    consumed,     \* 已消费的消息数
    closed        \* 通道是否关闭

这里使用VARIBALES关键字定义了四个状态变量，整个TLA+程序的函数逻辑就围绕这四个变量进行，TLC Model check也是基于这些状态变量对TLA+ module进行验证。

TypeOK ==
    /\ ch \in Seq(0..4)
    /\ produced \in 0..5
    /\ consumed \in 0..5
    /\ closed \in BOOLEAN

定义不变量，确保变量状态在系统的所有行为过程中始终保持在合理范围内，该TypeOK不变量即是整个程序的安全属性。

Init ==
    /\ ch = <<>>
    /\ produced = 0
    /\ consumed = 0
    /\ closed = FALSE

这是初始状态的公式，对应了四个变量的初始值。

Produce ==
    /\ produced < 5
    /\ ch = <<>>
    /\ ~closed
    /\ ch' = Append(ch, produced)
    /\ produced' = produced + 1
    /\ UNCHANGED <<consumed, closed>>

这里定义了生产操作的公式，只有在produced < 5，ch为空且closed不为true时，才会生产下一个数字。这里设定ch为空作为前提条件，主要是为了体现Channel的unbuffered的性质。

Close ==
    /\ produced = 5
    /\ ch = <<>>
    /\ ~closed
    /\ closed' = TRUE
    /\ UNCHANGED <<ch, produced, consumed>>

这里定义了关闭操作的公式，这里的ch = <<>>子公式的目的是等消费完之后再关闭channel，当然这里与Go的机制略有差异。

Consume ==
    /\ ch /= <<>>
    /\ ch' = Tail(ch)
    /\ consumed' = consumed + 1
    /\ UNCHANGED <<produced, closed>>

这里定义了消费操作的公式，只有channel不为空，才进行消费。

Next ==
    \/ Produce
    \/ Close
    \/ Consume

这里基于三个操作公式定义了下一个状态(Next)的公式，使用/运算符将这三个操作连接起来，表示下一步可以执行其中任意一个操作。

Fairness ==
    /\ SF_<<ch, produced, closed>>(Produce)
    /\ SF_<<produced, closed>>(Close)
    /\ SF_<<ch>>(Consume)

这里定义了公平性条件，确保各操作最终会被执行。

Spec == Init /\ [][Next]_<<ch, produced, consumed, closed>> /\ Fairness

这里定义了整个并发程序的规范，包括初始条件Init和下一步动作约束以及Fairness条件。/\连接的第二段Next表示系统的每一步都必须符合Next定义的可能动作，并且不会改变 <<ch, produced, consumed, closed>> 元组中变量之外的其他变量。Fairness 表示系统必须满足前面定义的 Fairness 条件。

THEOREM Spec => []TypeOK

这是一个定理，表示如果系统满足Spec规范，则一定会满足TypeOK这个不变量。其中的"=>"是蕴含的意思，A => B表示如果A为真，那么B必然为真。用一个例子可以解释这点，如果x > 3为真，那么 x > 1 必为真，我们可以将其写为：x > 3 => x > 1。

ChannelEventuallyEmpty == <>(ch = <<>>)
AllMessagesProduced == <>(produced = 5)
ChannelEventuallyClosed == <>(closed = TRUE)
AllMessagesConsumed == <>(consumed = 5)

这里定义了四个活性属性，用于在TLC Model check时验证最终状态使用，其中：ChannelEventuallyEmpty表示最终消息队列 ch 一定会为空；AllMessagesProduced表示最终一定会生产5条消息；ChannelEventuallyClosed表示最终消息队列一定会被关闭；AllMessagesConsumed表示最终一定会消费5条消息。

接下来，我们可以使用前面提到的TLA+ Toolbox来check该spec，下面是model的设置和model check的结果：

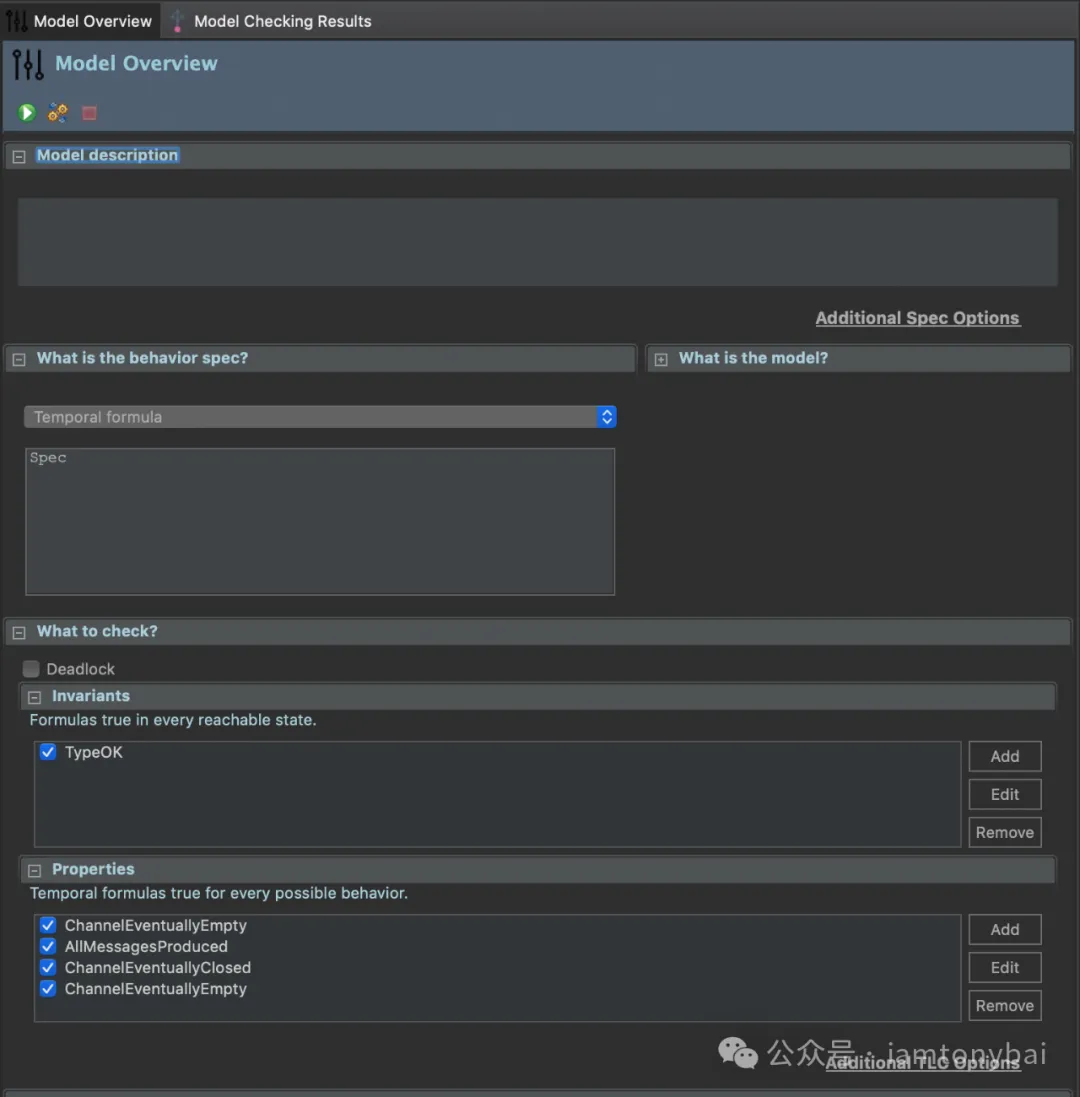model设置

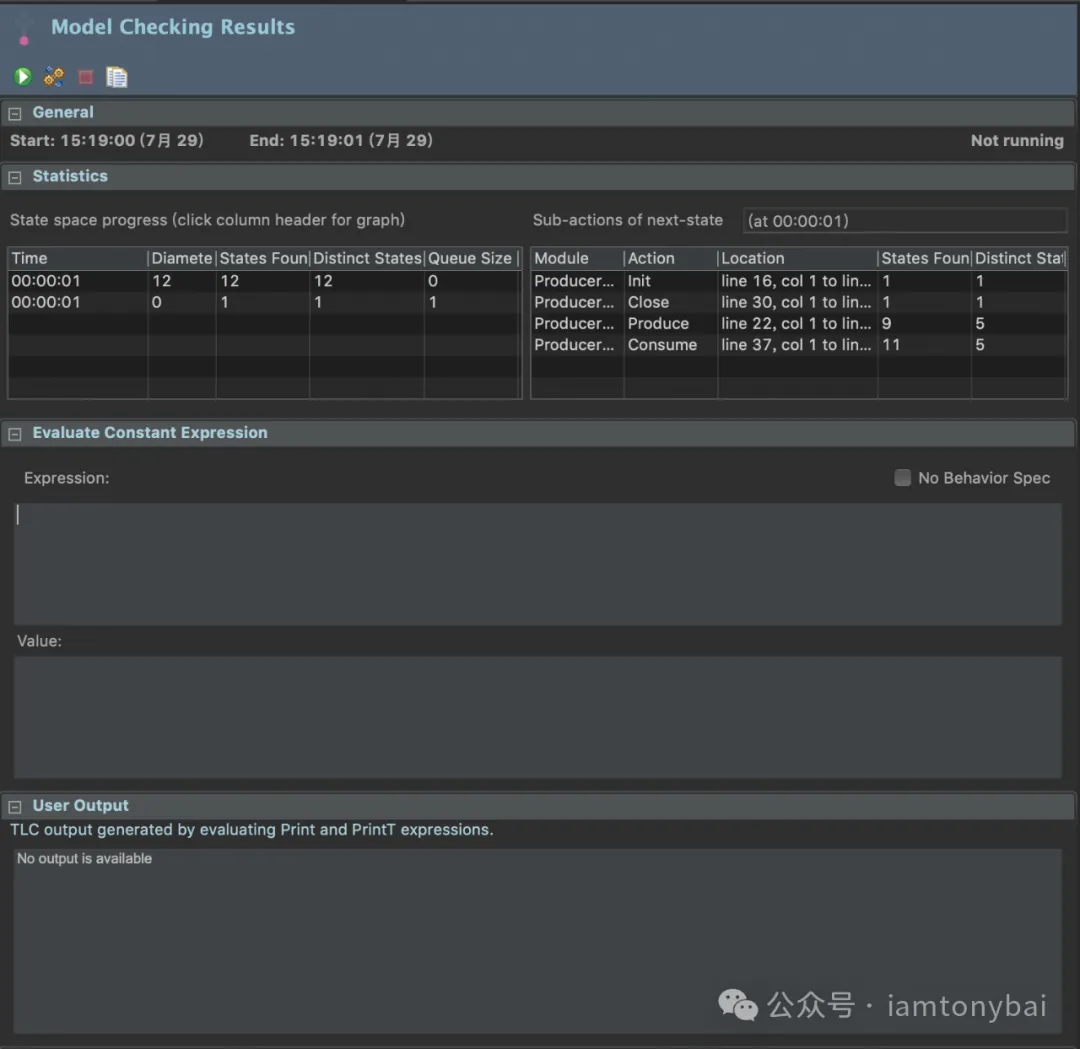check结果

注：在VSCode中使用TLA+插件的Checker对上述tla进行check，会出现不满足活性属性的error结果。

6. 小结

在这篇文章中，我们从Lamport提供的C语言代码示例出发，一步步介绍了如何将其转换为TLA+ spec，并使用TLA+ Toolkit进行验证。然后我们又以一个Go语言的生产者-消费者并发程序为例，展示了如何使用TLA+对其进行建模和验证。

不过我必须承认，TLA+这种形式化验证语言是极小众的。对大多数程序员来说，可能没什么实际帮助。即便是在大厂，真正使用TLA+对分布式系统进行形式化验证的案例也很少。

但是，我认为TLA+仍然有其独特的价值：

• 它迫使我们用更抽象和精确的方式思考系统设计，有助于发现潜在的问题。
• 对于一些关键的分布式系统组件，使用TLA+进行验证可以极大地提高可靠性。
• 学习TLA+的过程本身就是一次提升系统设计能力的过程。

当然，形式化方法并非万能。比如它无法解决性能退化等问题，也不能验证代码是否正确实现了设计。我们应该将其视为系统设计和验证的补充工具，而不是替代品。

总之，虽然TLA+可能不适合所有人，但对于那些构建复杂分布式系统的工程师来说，它仍然是一个值得学习和使用的强大工具。我希望这篇文章能为大家了解和入门TLA+提供一些帮助。

本文涉及的源码可以在这里[19]下载 - https://github.com/bigwhite/experiments/blob/master/go-and-tla-plus

本文部分源代码由claude 3.5 sonnet生成。

7. 参考资料

• The TLA+ Home Page[20] - https://lamport.azurewebsites.net/tla/tla.html
• 《Practical TLA+：Planning Driven Development[21]》- https://book.douban.com/subject/30348788/
• Learn TLA+[22] - https://www.learntla.com/
• 《[A Science of Concurrent Programs]》(https://lamport.azurewebsites.net/tla/science.pdf) - https://lamport.azurewebsites.net/tla/science.pdf
• 《Specifying Systems: The TLA+ Language and Tools for Hardware and Software Engineers[23]》- https://book.douban.com/subject/3752446/
• Linux Foundation Announces Launch of TLA+ Foundation[24] - https://www.linuxfoundation.org/press/linux-foundation-launches-tlafoundation
• TLA+ Foundation[25] - https://foundation.tlapl.us/
• TLA+ in TiDB[26] - https://github.com/pingcap/tla-plus
• TLA+ Web Explorer[27] - https://will62794.github.io/tla-web
• TLA+ language support for Visual Studio Code[28] - https://github.com/tlaplus/vscode-tlaplus
• Use of Formal Methods at Amazon Web Services[29] - https://lamport.azurewebsites.net/tla/formal-methods-amazon.pdf
• Leslie Lamport's The TLA+ Video Course[30] - https://www.youtube.com/playlist?list=PLWAv2Etpa7AOAwkreYImYt0gIpOdWQevD
• Leslie Lamport's The TLA+ Video Course homepage[31] - https://lamport.azurewebsites.net/video/videos.html
• Introduction to TLA+[32] - https://lamport.azurewebsites.net/video/video1-script.pdf
• TLA+ Google Group[33] - https://groups.google.com/g/tlaplus
• HILLEL WAYNE Blog[34] - https://www.hillelwayne.com/
• Leslie Lamport: Thinking Above the Code[35] - https://www.youtube.com/watch?v=-4Yp3j_jk8Q